具有不可關聯性的承諾方案

馬 麗，竇家維，吳艷梅

(陜西師范大學 數學與信息科學學院，陜西 西安 710119)

具有不可關聯性的承諾方案

馬 麗，竇家維，吳艷梅

(陜西師范大學 數學與信息科學學院，陜西 西安 710119)

承諾方案是密碼學中的一個基本方案，在密碼學中的其他協議中有重要的應用，比如：安全多方計算、加密方案、簽名方案、密鑰交換協議等。不可關聯的承諾方案是國際密碼學界的一個研究熱點，是實現電子拍賣的理論基礎，也是多方保密計算一個重要的模塊。不可關聯承諾方案在密碼學與實際應用中有很多用途，目前的研究主要集中于提高不可關聯承諾方案的安全性、效率以及減弱困難性假設等方面。因此，提出了兩種不可關聯承諾方案，能有效地阻止關聯攻擊和復制攻擊，且與其他方案相比效率更高。兩種不可關聯承諾方案分別基于離散對數假設和哈希函數性質的合理應用，如果能成功實施關聯攻擊就能夠計算離散對數，計算離散對數在密碼學中是難解問題，隨后給出了詳細的安全性證明和效率分析。研究分析表明，不可關聯承諾方案運用哈希函數作為承諾函數，效率以及安全性都比較高。

不可關聯承諾；離散對數假設；哈希函數；承諾函數

0 引 言

在保密拍賣中，拍賣方發布拍賣公告，公告拍賣商品的展示時間與拍賣截止時間。在拍賣截止時間之前，競價者寫好自己的出價，裝入信封并密封。截止日期過后，拍賣者在約定的開標時間，當著所有競價者的面打開信封，出價最高者獲得拍賣的商品。這是現實社會的拍賣過程。如果拍賣活動在網上進行，就成為網絡拍賣。無論現實拍賣還是網絡拍賣，都要保密進行。現實拍賣需要密封信封，密封信封的數字化對應物就是數字承諾[1]。

承諾協議分為兩個階段，承諾階段和揭示承諾階段。在承諾階段，承諾者根據自己的價格v，選擇一個隨機數r，計算承諾函數c=c(v,r)并發送給接收者，相當于把出價裝入密封信封。在這個階段，要求任意概率多項式時間的接收者都不能得到關于承諾值v的任何知識，即使接收者試圖進行欺騙，也無法得到相應知識，這個性質稱其為隱藏性。在揭示承諾階段，承諾者向接收者提供隨機數r和自己的承諾值v，接收者計算承諾函數c'=c(v,r)，如果c=c'，原承諾有效，否則拒絕，這個階段相當于當面打開信封。在這個階段，要求任意概率多項式時間的承諾者無法找到v≠v',r≠r'使得c(v,r)=c(v',r')，這個性質稱其為綁定性。

然而，一般的承諾協議具有可關聯性。假設Bob是關聯攻擊者，他不知道Alice的v，但可以利用Alice的c(v)得到c(v*)(v*=v+b)。如果這樣，在拍賣中Bob就可以用比Alice高一點的價格獲得拍賣商品，這是不公平的。為了克服關聯承諾造成的不公平，Dolev等提出了不可關聯承諾的概念[2]，并提出了一個著名的不可關聯承諾方案，其他學者也提出了一些不可關聯承諾方案[3-11]，但這些方案的效率都有待進一步提高。

因此，基于離散對數假設和哈希函數的性質，構造了兩種不可關聯承諾方案。這兩種方案簡單易行，安全性和效率都很高，計算復雜性和通信復雜性很低，可以作為其他密碼學協議的模塊并廣泛應用于其他實際安全問題中。

1 預備知識

1.1 難解問題

現代密碼學的安全性基于某些困難問題假設。難解問題是這樣一些問題，經過長時間研究，人們沒有找到這些問題的多項式時間算法或概率多項式時間算法，但也不能證明這些問題不存在多項式時間算法或者概率多項式時間算法。密碼系統的設計要使得攻擊者在不知道有關機密信息時，對密碼系統實施成功攻擊，必須要解某個難題。密碼學中的困難性問題主要有因子分解、離散對數、判斷n次剩余類問題[12]。

1.2 離散對數假設

αx≡βmodp

(1)

(2)

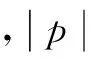
1.3 數字承諾方案

要理解數字承諾方案，需要理解兩個概念：安全性或隱藏性(secrecy or hiding)和歧義性(ambiguity)。

安全性：接收者即使任意偏離協議，也不能區分對于v的承諾c=c(v,r)和對于v'的承諾c'=c(v',r')，安全性保護承諾者的利益。

定義1[13]：數字承諾方案是概率多項式承諾者與接收者之間的一個交互協議，其中承諾者的輸入為v，協議同時滿足安全性和無歧義性。

1.4 基于離散對數假設的數字承諾方案

基于離散對數假設的數字承諾方案由Pedersen提出[14]，承諾協議如下：

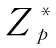
揭示承諾：承諾者將v,r發送給接收者，接收者驗證下述等式是否成立：

如果等式成立，承諾有效；否則無效。

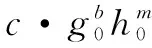
(4)

Bob看到了承諾者揭示的承諾值(v,r)后，他可以將(v+b,r+m)作為他的承諾值進行揭示，沒有人有理由懷疑他的承諾。如果攻擊者Bob這樣做，對于Alice是非常不公平的。為克服此承諾方案的可關聯問題，防止關聯攻擊，Dolev等提出了不可關聯承諾的概念[2]。

1.5 不可關聯承諾

有趣關系(interesting relation)：如果一個關系R?M×M是多項式時間可計算的非自反關系，則這個關系是有趣的。

不可關聯承諾：假設攻擊者知道v的承諾c=c(v,r)，仍然不能計算v*的承諾c*=c(v*,r')((v,v*)∈R)，則這個承諾稱為不可關聯承諾。

不可關聯承諾有如下兩種：

(1)關于承諾的不可關聯。

一個具有多項式計算能力的攻擊者知道關于v的承諾c=c(v,r)，只要能做出一個關于v*的承諾((v,v*)∈R)，不管他是否能夠成功地揭示這個承諾，都認為關聯成功。

一個承諾方案是關于承諾可關聯的，如果一個多項式計算能力的攻擊者能夠在這種意義下關聯成功。若任何具有多項式能力的攻擊者都不能在這種意義下關聯成功，就稱承諾方案是關于承諾不可關聯的。

(2)關于揭示的不可關聯。

一個具有多項式計算能力的攻擊者知道關于v的承諾c=c(v,r)，能夠做出一個c*=c(v*,r')((v,v*)∈R)，且能夠在揭示階段成功地揭示該承諾，才算關聯成功。一個承諾方案是關于揭示可關聯的，如果一個多項式計算能力的攻擊者在這種意義下關聯成功。若任何具有多項式能力的攻擊者都不能在這種意義下關聯成功，稱承諾方案是關于揭示的不可關聯。

如果一個承諾方案是關于承諾不可關聯的，那么它也一定是關于揭示不可關聯的。

1.6 Fischlin提出的不可關聯承諾方案

Fischlin提出了一個著名的不可關聯承諾方案[15]，該方案的思想是對協議1進行改進，要求承諾者在做出承諾之后，再用零知識證明的方法向接收者證明他確實知道他的承諾值。如果是真正的承諾者就容易證明，而攻擊者就無法完成零知識證明過程，因而無法完成承諾。協議如下：

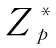
1)承諾階段。

將M,A,S發送給接收者。

(2)接收者選擇b∈Zp，并將b發送給承諾者。

2)揭示承諾階段。

(1)承諾者計算:

將a,u,r,y,z,v發送給接收者。

(2)接收者計算:

c≡a+bmodp

(3)接收者驗證:

若相等，則接受承諾；否則拒絕承諾。

協議1具有可關聯性，可能導致拍賣失敗，造成經濟損失。協議2中用附加零知識證明的方法解決了協議1中存在的關聯性問題，但是零知識證明的計算復雜性和通信復雜性都較高，因而效率較低。為提高不可關聯承諾的效率，設計了兩種不可關聯承諾方案。

2 兩種不可關聯承諾方案

2.1 基于離散對數的方案

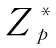
協議3：基于離散對數的承諾方案。

c(v)=(c1,c2,c3)=(gxmodp,gymodp,xv+2yamodp)

將c發送給接收者作為對v的承諾。

揭示承諾階段：承諾者把x,y發給接收者，接收者驗證:

(gxmodp,gymodp,xv+2yamodp)=(c1,c2,c3)

如果成立，則接受承諾；否則拒絕承諾。

直覺上，承諾者承諾的值是x的一個指數，攻擊者要想做出一個關于v+b的承諾，需要給c3乘以xb，這就必須知道x。要知道x，就必須求解離散對數。但求離散對數是困難的，所以該方案是不可關聯的。關于不可關聯性，有定理如下：

定理1：協議3構成一個承諾方案且是關于揭示不可關聯的。

要證明協議3構成一個數字承諾方案，需要下面的引理。

證明:首先證明安全性，假設對于v的承諾是：

(c1,c2,c3)=(gxmodp,gymodp,x(v+2)yamodp)

對于v'的承諾是：

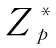
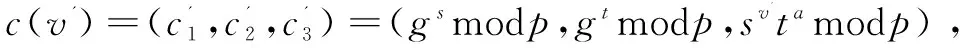
當Carol揭示承諾時，需要揭示s,t,v+1的值，就可以利用s,t,v計算α。

因為

所以

在這個方程中s,t,y,v都是已知的，都可以從方程中消除，最后得到一個xv+2modp≡u。利用費馬小定理可以很容易求出x=umodp。而根據離散對數假設，這是不可能的。所以方案是關于揭示不可關聯的。事實上，這個方案也是關于承諾不可關聯的。遺憾的是，目前還不能把它標準歸約到離散對數問題。

協議4:拍賣協議。

發送給拍賣者作為自己的秘密出價。

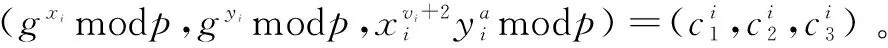
2.2 基于Pedersen的數字承諾方案的改進

協議設計：協議2是在協議1的基礎上增加零知識證明過程來阻止可能的關聯攻擊，注意到不用零知識證明的方法也可以阻止關聯攻擊，設計了一個基于單向散列函數的不可關聯承諾協議，就是在協議1的基礎上添加單向散列函數，同時將單向散列函數值作為承諾的一部分，使得承諾方案具有不可關聯性。具體協議如下：

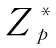
c2=c2(v,r)=hash(v‖r)

并將(c1,c2)發送給接收者。

揭示承諾階段：承諾者發送(v,r)給接收者，接收者驗證下述等式是否成立：

c2=c2(v,r)=hash(v‖r)

如果等式成立，則接受承諾值v；否則拒絕承諾值。

協議的正確性：

協議1是著名的承諾方案，文獻[10]已經證明它確實構成一個承諾方案。這里只證明增加單向散列函數確實能夠阻止關聯攻擊。

關聯攻擊者在看到(c1,c2)后，要想做出對v+b的承諾，必須選擇一個m,并計算：

c2=hash(x||r)

作為對x的承諾，把(c1,c2)給攻擊者。攻擊者得到(x+b,r+m)，就可以得到x。但根據離散對數假設，這是不可能的。

3 性能分析

Fischlin等提出了協議2，主要利用零知識證明的方法，使得承諾方案具有不可關聯性；分別利用離散對數和和哈希函數的性質提出了兩種不可關聯性的承諾方案；這里對協議2和兩種不可關聯承諾方案的計算復雜性和通信復雜性進行分析。

3.1 計算復雜性

在利用公鑰密碼系統構建的協議中，模指數運算的次數是決定協議效率的主要因素，因此協議的計算復雜性常常用模指數運算的次數衡量。一個協議需要的模指數運算次數越多，其計算復雜性越高，效率就越低。對這三種協議的計算復雜性，主要分析其模指數運算，而忽略計算復雜度低得多的模加法運算、單向散列函數運算等。協議2需要進行12次模指數運算，而協議3需要6次，協議5需要進行2次。

3．2 通信復雜性

協議的通信復雜性是傳遞數據的次數與傳送數據的比特數。傳遞的次數越多，則協議的通信復雜性越高。傳遞的比特越多，通信復雜性也越高。協議2中，通過3次傳遞完成了承諾和承諾的揭示過程，需要傳送的比特數為10lgp。協議3中，通過2次傳遞完成了數據的承諾與承諾揭示，需要傳送的比特數為2lgp。協議5中，通過2次傳遞完成了數據的承諾與承諾揭示，傳遞的比特數為lgp。(單向散列函數值的比特數通常比lgp的比特數少得多，因此可以忽略)

3.3 協議對比

計算復雜性與通信復雜性的全面比較見表1。表中計算復雜性指模指數運算的次數，通信復雜性指通信次數與傳遞數據的比特數。

表1 三種不可關聯性承諾的性能分析

4 結束語

由于不可關聯承諾方案有很多實際應用，提出了兩種新的不可關聯承諾方案。協議3是基于離散對數直接構造的方案，具有不可關聯性；協議5運用哈希函數，將Pedersen的基于離散對數假設的關聯承諾方案改進為一個不可關聯性承諾方案，并且提高了安全性。承諾方案的關鍵問題是如何找到簡單的承諾函數。因此，如何找到簡單的承諾函數并設計高效的承諾方案，是今后主要的研究方向。

[1] Hofheinz D,Quade J M.Universally composable commitments using random oracles[M]//Theory of cryptography.Berlin:Springer,2004:58-76.

[2] Dolev D,Dwork C,Naor M.Nonmalleable cryptography[J].SIAM Review,2003,45(4):727-784.

[3] Dachman-Soled D,Malkin T,Raykova M,et al.Adaptive and concurrent secure computation from new adaptive,non-malleable commitments[C]//Advances in cryptology-ASIACRYPT 2013.[s.l.]:[s.n.],2013:316-336.

[4] Abdalla M,Benhamouda F,Blazy O,et al.SPHF-friendly non-interactive commitments[C]//Advances in cryptology-ASIACRYPT 2013.[s.l.]:[s.n.],2013:214-234.

[5] Li Shundong,Wang Daoshun,Dai Yiqi,et al.New method for constructing non-malleable commitment schemes[J].Chinese Journal of Electronics,2008,17(4):583-588.

[6] Ishai Y, Kushilevitz E, Ostrovsky R.Sufficient conditions for collision-resistant hashing[M]//Theory of cryptography.Berlin:Springer,2005:445-456.

[7] Haitner I, Nguyen M H, Ong S J,et al.Statistically hiding commitments and statistical zero-knowledge arguments from any one-way function[J].SIAM Journal on Computing,2009,39(3):1153-1218.

[8] Brenner H,Goyal V,Richelson S,et al.Fast non-malleable commitments[C]//Proceedings of the 22nd ACM SIGSAC conference on computer and communications security.[s.l.]:ACM,2015:1048-1057.

[9] Pass R.Unprovable security of perfect NIZK and non-interactive non-malleable commitments[M]//Theory of cryptography.Berlin:Springer,2013:334-354.

[10] Naor M.Bit commitment using pseudorandomness[J].Journal of Cryptology,1991,4(2):151-158.

[11] Goldreich O. Foundations of cryptography:basic tools[M].London:Cambridge University Press,2001.

[12] 李順東,王道順.現代密碼學[M].北京:科學出版社,2009.

[13] Paillier P.Public-key cryptosystems based on composite degree residuosity classes[C]//Advances in cryptology-EUROCRYPT’99.[s.l.]:[s.n.],1999:223-238.

[14] Pedersen T P.Non-interactive and information-theoretic secure verifiable secret sharing[C]//Advances in cryptology-CRYPTO’91.[s.l.]:[s.n.],1992:129-140.

[15] Fischlin M,Fischlin R.Efficient non-malleable commitment schemes[C]//Advances in cryptology-CRYPTO 2000.[s.l.]:[s.n.],2000:413-431.

Non-malleable Commitment Schemes

MA Li,DOU Jia-wei,WU Yan-mei

(College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710119,China)

Commitment scheme is a basic scheme in cryptography and has been important application in other agreements of cryptography like secure multi-party computation,encryption scheme,signature scheme,key exchange protocols and so on.Non-malleable commitment scheme is one focus in the international cryptographic community and the theoretical basis of electronic auction,which is also an important building block of secure multi-party computation and has important applications in cryptography and practice.At present,most studies focus on improving the security and the efficiency of non-malleable commitment schemes and less difficulty hypothesis,etc.So,two non-malleable commitment schemes are proposed which can efficiently prevent malleable attack and copy attack.These non-malleable commitment schemes are constructed based on discrete logarithm assumption and one-way hash function.If adversary can successfully attack the scheme,it can compute the discrete logarithm.The computing discrete logarithm in cryptography is a hard problem,and its security proving and efficiencies analysis are given.Study analysis shows that non associated commitment scheme using hash function as a commitment function,efficiency and security are relatively high.

non-malleable commitment;discrete logarithm assumption;hash function;commitment function

2016-06-07

2016-09-15 網絡出版時間：2017-03-07

國家自然科學基金資助項目(61272435)

馬 麗(1983-)，女，碩士研究生，研究方向為密碼學與信息安全；竇家維，副教授，碩士生導師，研究方向為密碼學與信息安全。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170307.0922.070.html

TP301

A

1673-629X(2017)05-0108-05

10.3969/j.issn.1673-629X.2017.05.023