具有時變時延和丟包的網絡控制系統H∞控制
周 穎,鄭 鳳,何 磊
(南京郵電大學 自動化學院,江蘇 南京 210003)
具有時變時延和丟包的網絡控制系統H∞控制
周 穎,鄭 鳳,何 磊
(南京郵電大學 自動化學院,江蘇 南京 210003)
針對一類同時具有時變時延和丟包的網絡化控制系統,設計使得閉環系統均方意義下指數穩定的H∞狀態反饋控制器,并且滿足給定的H∞性能指標。已知系統從傳感器到控制器之間通道具有數據包丟失和時變時延,控制器到執行器通道具有時變時延。假設網絡誘導總時延小于等于一個采樣周期,將時延的時變系數轉換為系統參數矩陣的不確定性,因此系統被建模為范數有界的不確定系統。使用Bernoulli隨機序列描述數據包丟失且數據丟失概率已知。基于線性矩陣不等式(LMI)方法和李雅普諾夫(Lyapunov)穩定性原理,給出并證明了所設計控制器存在的充分條件,并將控制器設計問題轉換為求解線性矩陣不等式可行解的問題。最后給出了仿真實例,驗證了采用的設計控制器方法的有效性和可行性。
時變時延;丟包;網絡控制系統;H∞控制;線性矩陣不等式
0 引 言
在過去十年中,通信、計算機以及控制技術的飛速發展,大大地影響了控制系統的結構。隨著控制對象復雜度的增加,控制區域的擴大,傳統的控制系統已經滿足不了復雜的需求。因此,網絡控制系統(NCS)應運而生[1-3]。
在NCS給人們帶來極大便利的同時,由于網絡自身的特性,也給設計和分析NCS帶來了麻煩。其中突出的兩個問題就是時延和丟包。網絡控制系統在數據傳輸過程中往往伴隨著時延和丟包。設計一個現實的NCS必須要考慮到時延和丟包對系統的影響,否則將會導致系統性能下降甚至失穩[4-7]。
關于網絡控制系統丟包和時延的問題,很多文獻都給出了解決方法[8-10]。文獻[11]考慮了傳感器到控制器之間的時延和丟包,用Markov隨機序列描述數據丟失并且設計了一個狀態反饋控制器使得系統達到穩定。文獻[12]用Bernoulli隨機序列描述丟包,丟包的概率屬于一個已知的區間。文獻[13]針對具有隨機時延的NCS設計H∞控制器,隨機時延滿足Bernoulli隨機序列。文獻[14]假設系統時延恒定,將系統動態地分成多種情況來考慮,用多個子系統描述不同丟包情況下的網絡化系統模型。
文獻[15]假設網絡控制系統的時延為一步時延,方便了對系統的分析,卻人為地增加了網絡時延。文獻[16]在處理時延時,采用在控制器和執行器接收端設置緩沖區的方法,隨機時延即被轉為確定時延,實際處理的時延是定常時延。文獻[17]討論了具有一步時延和丟包的網絡控制系統的H∞濾波器的設計問題,用兩個不相關的Bernoulli隨機序列分別描述一步時延和丟包。
現如今,針對具有時延和丟包的網絡控制系統的研究已經有很多成果,但仍然存在不足。網絡誘導時延由前向通道和反饋通道的時延組成,上述有些文獻只解決了前向通道的時延。有些文獻只考慮時延或丟包其中一種情況下NCS的控制問題。而有的文獻即使同時考慮到時延和丟包,但均是假設網絡誘導時延是已知的常數。事實上,時延和丟包總是同時發生的,而且時延并不一定是常數,丟包也具有隨機性。
針對上述情況,研究了具有時延和丟包的網絡控制系統的H∞控制。不僅考慮了傳感器到控制器的時延,也考慮了控制器到執行器之間的時延,并且假設時延是時變的,將未知的時延變量處理成系統參數的不確定性,利用Bernoulli隨機序列描述數據丟失。通過LMI和Lyapunov函數給出了H∞控制器存在的充分條件。
1 問題描述
具有時延和丟包的網絡控制系統的結構如圖1所示。
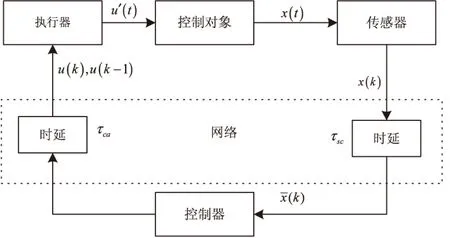
圖1 系統結構圖
圖中,τsc表示傳感器到控制器通道之間的時延,τca表示控制器到執行器通道之間的時延。網絡誘導總時延為τk(τk=τsc+τca)。文中時延考慮為時變短時延,所以τk∈[0,T],T為一個采樣周期。假設丟包發生在前向通道,滿足Bernoulli隨機序列且概率已知。
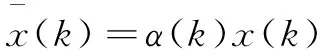
(1)
其中,α(k)是一個Bernoulli隨機序列,其值可取0或1,滿足如下概率:
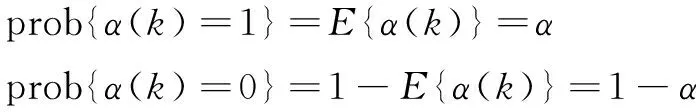
(2)
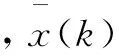
考慮如下的線性時不變系統:
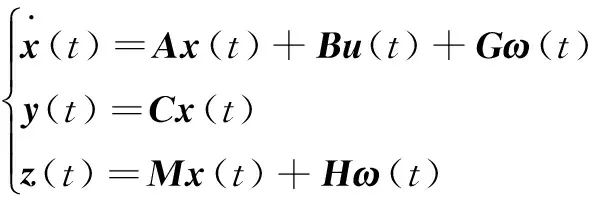
(3)
其中,u(t)∈Rm,x(t)∈Rn,y(t)∈Rp,z(t)∈Ro,ω(t)∈Rq分別表示控制輸入、系統狀態、系統輸出、控制輸出和外部干擾;A,B,C,G,H,M為具有適當維數的已知矩陣。
對方程(3)進行離散化,得到:
(4)
其中:
(5)
其中,λ1,λ2,…,λn為矩陣A的特征值;Λ1,Λ2,…,Λn是矩陣A的特征向量。
F(τk)滿足:
FT(τk)F(τk)≤I
(6)
針對系統(3),設計如下的狀態反饋控制器:
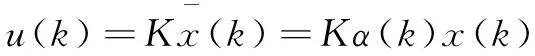
(7)
將式(7)代入式(4),得到閉環控制系統的方程為:
(8)
針對閉環控制系統(8),設計形如式(7)的控制器,滿足:
(1)閉環系統(8)均方意義下指數穩定;
(2)零初始條件下,系統控制輸出滿足:
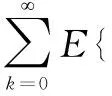
(9)
其中,γ給定且大于0。
以下是證明閉環系統(8)穩定性時用到的引理:
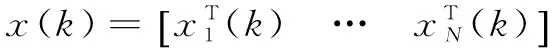
引理2:V(x(k))為Lyaponuv函數,如果存在正實數λ≥0,μ>0,ν>0和0<ψ<1滿足:
μ‖x(k)‖2≤V(x(k))≤v‖x(k)‖
E{V(x(k+1))|x(k)}-V(x(k))≤
λ-ψV(x(k))
(10)
那么有:
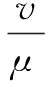
(11)
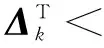
(12)
則存在任意正數ε使得:
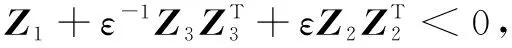
(13)
2 主要結果
當ω(k)=0時,對于系統(8),得到定理1。
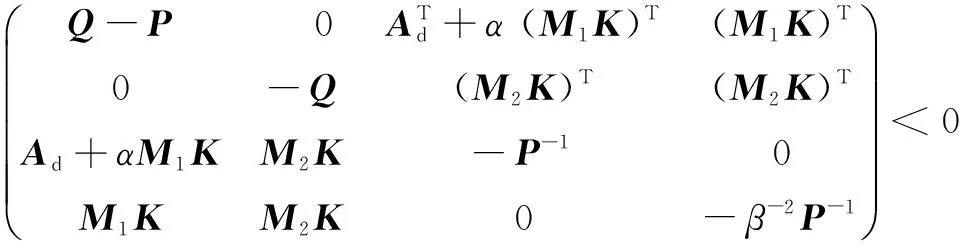
(14)
其中:
(15)
那么系統(8)均方意義下指數穩定。
證明:ω(k)=0時,構造如下的Lyaounov函數:
V(x(k))=xT(k)Px(k)+xT(k-1)Qx(k-1)
(16)
可得:
V(x(k+1))=xT(k+1)Px(k+1)+xT(k)Qx(k)
(17)
式(16)與式(17)兩項作差可得:
取ηT(k)=[x(k),x(k-1)]T,因為E{α(k)-α}=0,E{(α(k)-α)2}=(1-α)α=β2,令M1=B0+DF(τk)E,M2=B1-DF(τk)E,得到:
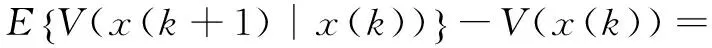
[Adx(k)+(α(k)-α)M1Kx(k)+αM1Kx(k)+(α(k)-α)M2Kx(k-1)+αM2Kx(k-1)]TP[Adx(k)+ (α(k)-α)M1Kx(k)+αM1Kx(k)+ (α(k)-α)M2Kx(k-1)+αM2Kx(k-1)]+xT(k)Qx(k)-xT(k)Px(k)-xT(k-1)Qx(k-1)= [Adx(k)+αM1Kx(k)+αM2Kx(k-1)]TP[Adx(k)+αM1Kx(k)+αM2Kx(k-1)]+β2[M1Kx(k)]TP[M1Kx(k)]+β2[M1Kx(k)]TP[M2Kx(k-1)]+β2[M2Kx(k-1)]TP[M1Kx(k)]+β2[M2Kx(k-1)]TP[M2Kx(k-1)]+xT(k)Qx(k)-xT(k)Px(k)-xT(k- 1)Qx(k-1)=ηT(k)θ1η(k)
(18)
由Schur補引理可知,式(14)等價于θ1<0,得到:
E{V(x(k+1)|x(k))}-V(x(k))=ηT(k)θ1η(k)≤-λmin(θ1)ηT(k)η(k)< -γηT(k)η(k)
(19)
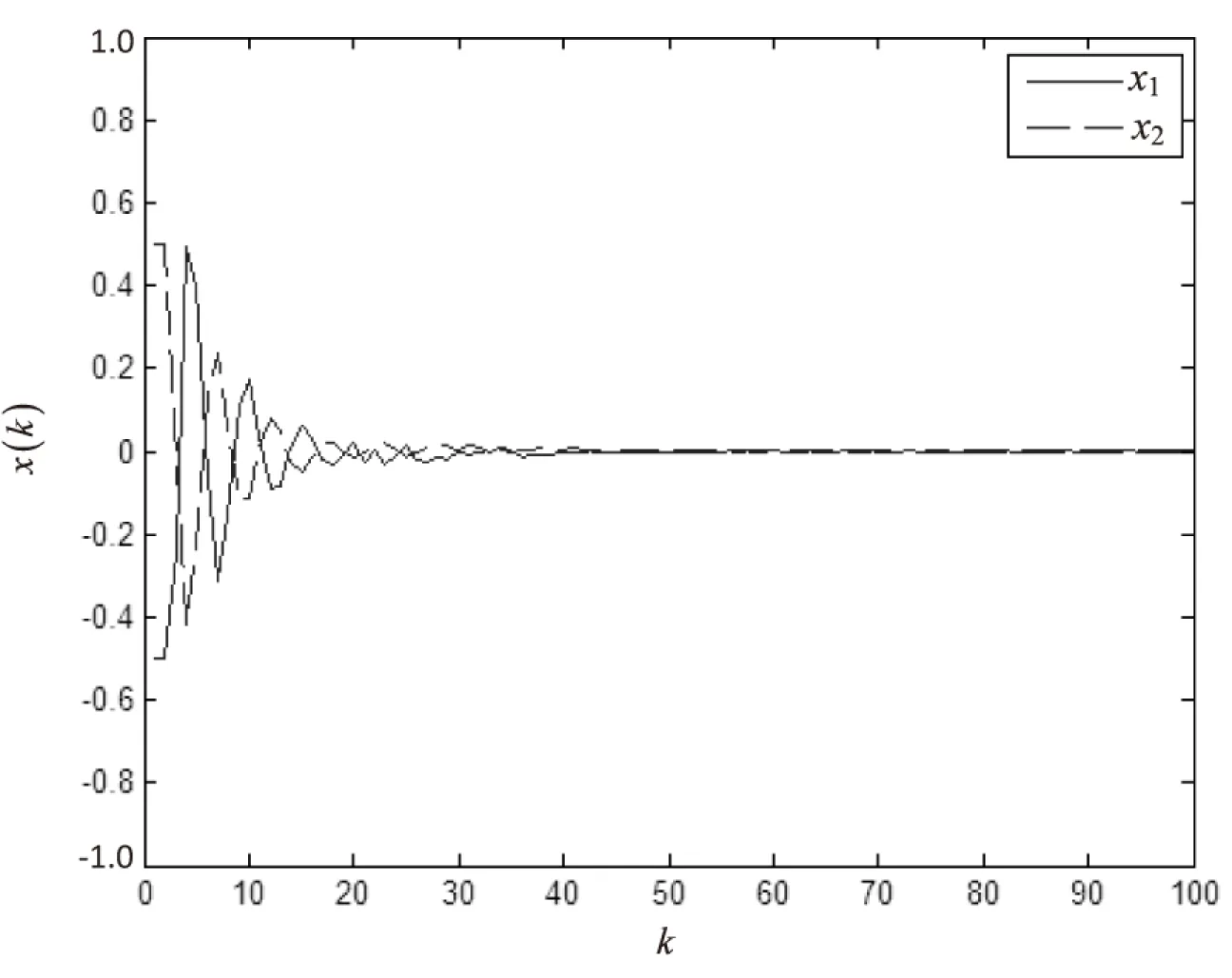
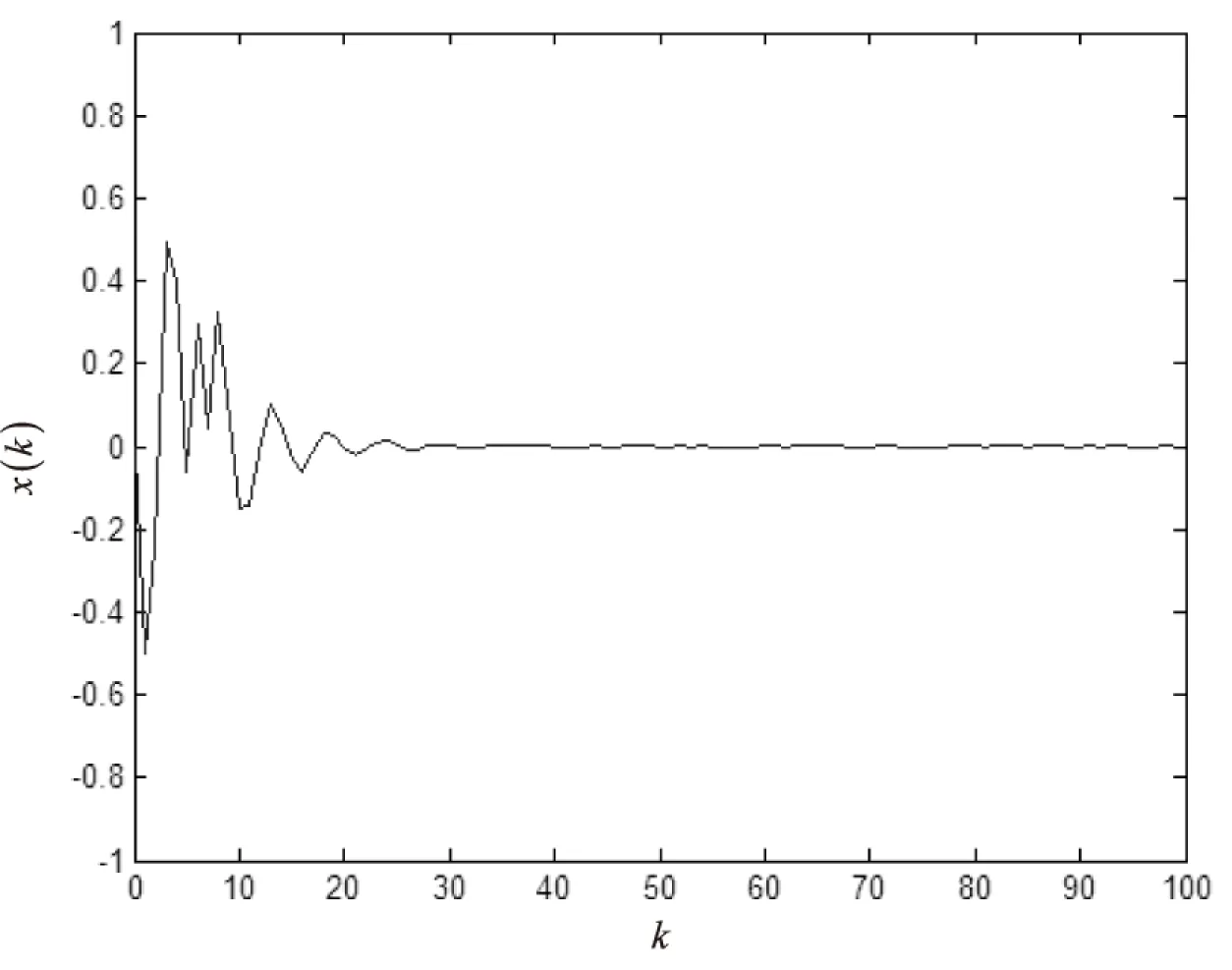
其中,0<γ 令σ=λmax(P),得到: E{V(x(k+1)|x(k))}-V(x(k))< (20) 由引理1和引理2可知,閉環控制系統(8)均方意義下指數穩定。 ω(k)≠0時,對于閉環系統(8)設計滿足均方意義下指數穩定的H∞控制器,給出定理2和定理3。 定理2:對式(8),干擾輸入ω(k)≠0,給定γ>0,若存在正定對稱矩陣P,Q和增益矩陣K,滿足: (21) 那么系統(8)均方意義下指數穩定且滿足H∞性能。 證明:當ω(k)=0時,容易證得閉環系統(8)均方意義下指數穩定。 當ω(k)≠0時,取Lyapunov函數V(x(k))=xT(k)Px(k)+xT(k-1)Qx(k-1),取ηT(k)=[x(k),x(k-1),ω(k)]T,進而得到: (22) 由Schur補引理可知,式(21)等價于θ2<0,此時有 E{V(0)}-E{V(∞)},由零初始條件可知E{V(0)}=0,得到: (23) 證畢。 定理3:給定γ>0,ε>0,對于系統(8),若存在正定對稱矩陣X,Y和矩陣Z滿足: (24) 那么系統(8)均方意義下指數穩定且滿足H∞性能。 證明:由式(21)可知: (25) 左右同乘diag{P-1,P-1,I,I,βI,I,I},令Y=P-1QP-1,X=P-1,Z=KP-1。不等式(25)可化為式(24)。由引理1可知,閉環系統(8)均方意義下指數穩定且滿足給H∞性能。證畢。 考慮如下的控制對象: (26) 令F(τk)中的α1=0,α2=0。 根據如上假設,可以得到: 給定γ=1,ε=4,通過Matlab中的LMI工具求解式(24)得出: 當ω(k)=0時,由Matlab仿真工具可得閉環系統的狀態響應圖,如圖2所示。 圖2 ω(k)=0時閉環系統的狀態響應圖 與此同時,可以得到: 滿足H性能指標。由圖可以看出系統是穩定的,所以采用的方法是可行的。 圖3 ω(k)≠0時閉環系統的狀態響應圖 圖4 ω(k)≠0時閉環系統的輸出響應圖 對于同時具有時延和丟包的網絡控制系統,假設時延存在于傳感器到控制器之間和控制器到執行器之間且時延是時變的。將時變短時延系統建模成含有不確定參數的系統。利用Lypunov穩定性原理和LMI方法給出并證明了H∞控制器存在的充分條件。由仿真實例證明了設計的控制器是可行有效的。 [1] 陳志明,崔寶同.數據包丟失的無線網絡控制系統的故障檢測[J].計算機技術與發展,2012,22(11):61-64. [2]HetelL,DaafouzJ,IungC.Stabilizationofarbitraryswi-tchedlinearsystemswithunknowntime-varyingdelays[J].IEEETransactionsonAutomaticControl,2006,51(10):1668-1674. [3]JungEH,LeeHH,SuhYS.LMI-basedoutputfeedbackcontrolofnetworkedcontrolsystems[C]//IEEEinternationalworkshoponfactorycommunicationsystems.[s.l.]:IEEE,2004:311-314. [4]ZhangY,TangGY,HuNP.Non-fragilecontrolfornonlinearnetworkedcontrolsystemswithlongtime-delay[J].Computers&MathematicswithApplications,2009,57(10):1630-1637. [5]ZhangHK.Non-fragileguaranteed-costrobusth-infinitycontrolforaclassofnonlinearnetworkedcontrolsystemswithlongtime-delay[C]//2010internationalconferenceonintelligentcomputationtechnologyandautomation.[s.l.]:IEEE,2010:784-787. [6]FridmanE,ShakedU.AdescriptorsystemapproachtoH∞controloflineartime-delaysystems[J].IEEETransactionsonAutomaticControl,2002,47(2):253-270. [7]ChenZP,LiuL,ZhangJF.Observerbasednetworkedcontrolsystemswithnetworked-inducedtimedelay[C]//Internationalconferenceonsystems.[s.l.]:IEEE,2004:3333-3337. [8]MahmoudMS,KhanGD.DynamicoutputfeedbackofnetworkedcontrolsystemswithpartiallyknownMarkovchainpacketdropouts[J].OptimalControlApplicationsandMethods,2015,34(5):505-634. [9] 黃 鶴,韓笑冬,謝德曉,等.具有數據包丟失的網絡控制系統主動容錯控制[J].控制與決策,2009,24(8):1126-1131. [10]DasguptaS,HalderK,BanerjeeS,etal.StabilityanalysisandcontrollersynthesisofNetworkedControlsystem(NCS)witharbitrarypacketdrop-outs[C]//2ndinternationalconferenceonelectronicsandcommunicationsystems.[s.l.]:IEEE,2015:217-222. [11] 馬衛國,邵 誠.網絡控制系統隨機穩定性研究[J].自動化學報,2007,33(8):878-882. [12] 阮玉斌,楊富文,王 武.測量丟失概率不確定的網絡化系統的魯棒故障檢測[J].控制與決策,2008,23(8):894-899. [13]YangFW,WangZD,HungYS,etal.H∞controlfornetworkedsystemswithrandomcommunicationdelays[J].IEEETransactionsonAutomaticControl,2006,51(3):511-518. [14] 邱占芝,張慶靈,連志春,等.存在時延和數據包丟失情況下狀態反饋網絡控制系統的指數穩定性[J].信息與控制,2005,34(5):567-575. [15]ZhouY,ZhuYJ.Controlforuncertaindiscrete-timesystemwithdatapacketdropoutsandonestepdelay[C]//34thChinesecontrolconference.[s.l.]:[s.n.],2015:6777-6781. [16] 于之訓,陳輝堂.時延網絡控制系統均方指數穩定的研究[J].控制與決策,2000,15(3):278-281. [17] 李秀英,王金玉,孫書利.具有一步隨機時滯和多丟包的網絡系統H∞濾波器設計[J].自動化學報,2014,40(1):155-160. H∞ Control of Networked Control Systems with Time-varyingDelay and Packet Dropout ZHOU Ying,ZHENG Feng,HE Lei (College of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210003,China) For a class of networked control systems with time-varying delay and packet dropout,aH∞controllerisdesignedinordertomaketheclosed-loopsystemmeansquarestableandmeettheprescribedH∞disturbanceattenuationlevel.Itisknownthatthesystemhasdatapacketlossandtime-varyingdelayfromthesensortothecontroller,andtimevaryingdelayfromthecontrollertoactuator.Thetotaltimedelayislessthanonesamplingperiod.Theuncertaintyofdelayisturnedintotheunknownparametersofthesystemequationsothatthesystemismodeledasanormboundeduncertainsystem.DatapacketdropoutisassumedtobesatisfiedwiththeBernoullidistributionsequencewithknownprobability.SufficientconditionsfortheexistenceofthestatefeedbackcontrolleraregivenbylinearmatrixinequalityandLyapunovprinciple.Andthecontrollerdesignproblemistransformedintosolvingthefeasiblesolutionofthelinearmatrixinequality.Asimulationexampleisgiventoprovetheeffectivenessandfeasibilityofthedesignmethod. time-varying delay;packet dropout;networked control system;H∞control;linearmatrixinequality 2016-05-31 2016-09-02 網絡出版時間:2017-03-13 國家自然科學基金資助項目(61104103,61102155) 周 穎(1978-),女,博士,副教授,碩士生導師,研究方向為網絡化控制系統的分析與設計、復雜大系統的自適應控制、非線性系統的控制理論及應用;鄭 鳳(1992-),女,碩士研究生,研究方向為網絡化控制系統的分析與設計。 http://kns.cnki.net/kcms/detail/61.1450.tp.20170313.1545.032.html TP A 1673-629X(2017)05-0164-06 10.3969/j.issn.1673-629X.2017.05.034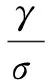
3 仿真實例
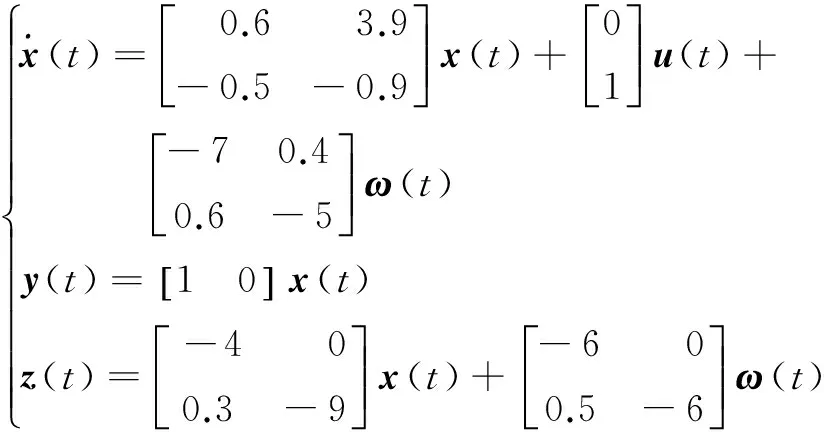
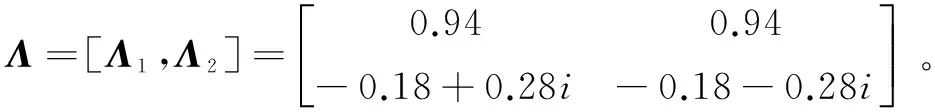

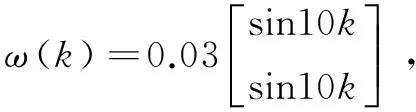
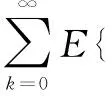
4 結束語

