分位數回歸區間估計方法比較分析

袁曉惠， 鞠婷婷， 陳 晶

(長春工業大學 基礎科學學院， 吉林 長春 130012)

?

分位數回歸區間估計方法比較分析

袁曉惠， 鞠婷婷， 陳 晶

(長春工業大學 基礎科學學院， 吉林 長春 130012)

介紹了分位數回歸模型參數的3類區間估計方法，分別為直接法、自助法、誘導光滑法,通過模擬比較他們在覆蓋率與置信區間長度方面的表現。

分位數回歸； 誘導光滑； 自助法

0 引 言

線性回歸模型是統計學中最經典的模型。傳統的線性回歸研究因變量的條件均值隨自變量的變化趨勢。此類模型對隨機誤差的分布有較強的假定。Koenker和Bassett[1]于1978年提出線性分位數回歸，考慮因變量的條件分位數對自變量的影響，可以根據不同的條件分位數更全面地認識因變量的條件分布。與傳統的線性回歸相比，分位數回歸模型使用范圍更廣，估計效果更準確。隨著計算機技術的發展，分位數回歸模型在經濟、金融、生物醫學、數據挖掘、環境科學等方面得到廣泛應用[2-3]。

分位數回歸模型的目標函數是非光滑的，其參數的估計存在一定的困難。針對分位數回歸模型參數的區間估計問題，比較流行的有4類方法：

1)直接法。根據參數估計的漸近正態性，運用樣本信息直接估計漸近方差中的未知量并構造置信區間。

2)秩得分法。根據秩檢驗統計量的反演運算構造置信區間。此方法易于理解，計算簡單，但是計算速度較慢，尤其在處理大型多維數據時，此算法運行緩慢。

3)自助法[4]。基于重復抽樣技術構造回歸參數的置信區間。

4)誘導光滑法[5-6]。此方法給參數添加一個正態隨機擾動，對不光滑的估計函數在這個擾動下求期望，得到一個新的光滑估計函數，然后基于這個新的光滑估計函數得到回歸參數的估計。

經過迭代，誘導光滑方法可以同時得到參數的點估計及其協方差估計，進而得到回歸參數的區間估計。由于此方法不需要額外確定調諧參數(如核估計的窗寬)，此估計方法得到廣泛應用[7-9]。

文中主要介紹直接法、自助法、誘導光滑法構造分位數回歸模型區間估計的算法步驟，并通過模擬比較這3種方法構造的置信區間的覆蓋率和平均置信區間長度。

1 分位數回歸模型及其區間估計

假定得到觀測數據為(xi,yi)(1≤i≤n)，yi是響應變量，xi是p維協向量，分位數回歸模型如下:

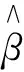
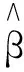
其中

1.1 直接法

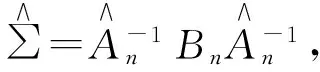
這里hn是窗寬，當n→，hn→0，根據Hall和Sheather[12]方法選取

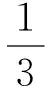
1.2 自助法

自助法是Efron[4]于1979年提出的一種再抽樣統計方法，通過不斷地從原始數據集中有放回抽取新樣本，組成新的數據集。漸近理論保證了基于新的數據集計算的估計量與基于原始數據集的估計量有相同的漸近分布。此方法適用于那些難以用常規方法(如極大似然法、矩估計法等)導出參數的區間估計、假設檢驗等問題。

文中主要介紹如下兩種自助法。

1.2.1 成對數據自助法

Arcones和Gine[13]提出成對自助法來構造M-估計的置信區間。成對數據自助法的步驟如下：

1)令 b=1；

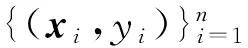
4)重復步驟2)和3)，直到產生B個β的估計。

1.2.2 加權自助法

Jin[14]等2001年提出一種通過擾動目標函數的重抽樣方法。Tang和Leng[15]運用此方法構造縱向數據分位數回歸參數的置信區間。此方法應用于分位數回歸區間估計的步驟如下：

1)令b=1；

2)從參數為1的指數分布中產生隨機數Vi～exp(1),i=1,2，…,n；

4)重復步驟2)和3)，直到產生B個β的估計。

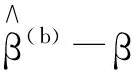
1.3 誘導光滑法

誘導光滑法最初是由Brown和Wang[5]于2005年提出，用于估計秩估計的漸近方差。Wang[6]等將之用于構造分位數回歸區間估計。由于此光滑方法不像核估計等需要額外估計窗寬，使之得到許多統計學家的青睞。

誘導光滑算法步驟如下：

1)設定Γ的初始值：Γ(0)=n-1Ip；

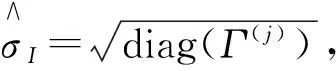
2 模擬比較

通過模擬研究從置信區間長度和覆蓋率兩個角度來比較上述3類方法在構造分位數回歸參數的置信區間上的表現。從如下分位數回歸模型產生數據(xi,yi)(1≤i≤n)：

yi=β0+xiβ1+σ(xi)(εi-Qτ(εi))

i=1,2,…,n

β的置信水平為95%的置信區間的平均長度和覆蓋率(σ(xi)=1)見表1。

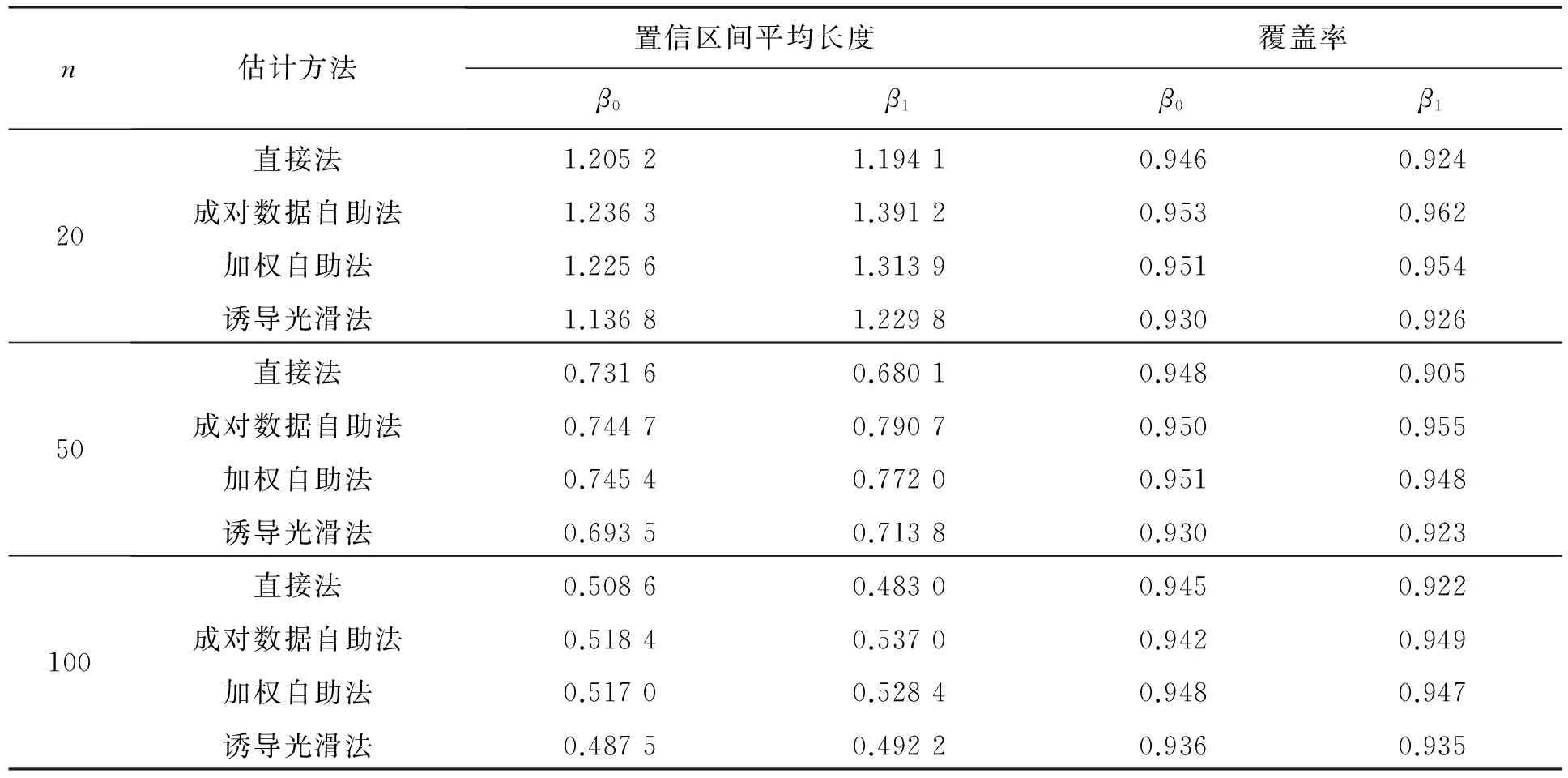
表1 β的置信水平為95%的置信區間的平均長度和覆蓋率(σ(xi)=1)

從表1可以看出，直接法和誘導光滑法的置信區間平均長度比自助法估計的置信區間長度短。當樣本量為20時，直接法和誘導光滑法的覆蓋率較低，但是當樣本量增至50和100時，他們的覆蓋率都有所增加。

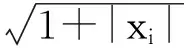
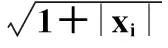
表2 β的置信水平為95%的置信區間的平均長度和覆蓋率(σ(xi)=)

表2中，直接法的覆蓋率較低。隨著樣本量增大，覆蓋率也沒有增加,說明直接法需要誤差獨立同分布的假定。當誤差不是獨立同分布時，構造的置信區間不是很好,而自助法和誘導光滑法的覆蓋率都能接近95%。雖然誘導光滑法的平均置信區間長度相比于自助法要短，但是當樣本量較小時，誘導光滑法的覆蓋率偏低。自助法中成對數據自助法的平均置信區間長度相對長一些，在覆蓋率接近95%時，加權自助法的平均置信區間長度相對短一些。加權自助法在小樣本時表現較出色。

3 結 語

分別介紹了3類區間估計方法的算法，并通過模擬比較他們在覆蓋率與置信區間長度方面的表現。從模擬結果可以看出，在直接法中，由于用核估計方法來估計漸近方差中未知的密度函數，依賴于誤差獨立同分布的假定。如果誤差分布不是獨立同分布時，此估計效果不是很理想。重復抽樣法計算估計的算法雖然需要上百次的重新計算估計,計算量比較大，但是覆蓋率較好。誘導光滑法計算方法簡單，其估計的置信區間長度最小，但是在小樣本時覆蓋率較低。建議如果數據樣本量比較小時，考慮用加權自助法估計參數的置信區間，當樣本量較大時，用誘導光滑法構造參數的置信區間。

[1] Koenker R， Bassett G. The asymptotic distribution of the least absolute error estimator[J]. Journal of the American Statistical Association，1978,73:618-622.

[2] 王純杰，董小剛，陳嘉，等.基于分位數回歸的長春市職工工資水平的分析[J].長春工業大學學報：自然科學版，2010,31(4):367-373.

[3] 何大強，張海燕.吉林省農村居民消費水平分析[J].長春工業大學學報：自然科學版，2013,34(4):452-456.

[4] Efron B. Bootstrap methods: another look at the Jackknife [J]. Annals of Statistics,1979,7(1):1-26.

[5] Brown B M, Wang Y G. Standard errors and covariance matrices for smoothed rank estimators [J]. Biometrika,2005,92(1):149-158.

[6] Wang Y, Shao Q, Zhu M, et al. Quantile regression without the curse of unsmoothness [J]. Computational Statistics & Data Analysis,2009,53(10):3696-3705.

[7] Pang L, Lu W, Wang H. Variance estimation in censored quantile regression via induced smoothing [J]. Computational Statistics and Data Analysis,2012,56(4):785-796.

[8] Leng C, Zhang W. Smoothing combined estimating equations in quantile regression for longitudinal data [J]. Statistics and Computing,2014,24(1):123-136.

[9] Lu X, Fan Z. Weighted quantile regression for longitudinal data [J]. Computational Statistics,2015,30(2):569-592.

[10] Koenker R. Quantile regression [M]. Cambridge: Cambridge University Press,2005.

[11] Koenker R, Machado J A F. Goodness of fit and related inference processes for quantile regression [J]. Journal of the American Statistical Association,1999,94(448):1296-1310.

[12] Hall P, Sheather S J. On the distribution of a studentized quantile [J]. J. R. Stat. Soc. B.，1988,50:381-391.

[13] Arcones M, Gine E. On the bootstrap of M-estimators and other statistical functionals[C]// In R. LePage & L. Billard (eds.), Exploring the Limits of Boorstrap，1992：13-47.

[14] Jin Z, Ying Z, Wei L J. A simple resampling method by perturbing the minimand[J]. Biometrika,2001,88(2):381-390.

[15] Tang C Y, Leng C. Empirical likelihood and quantile regression in longitudinal data analysis[J]. Biometrika,2011,98(4):1001-1006.

Comparison analysis of quantile regression interval estimation

YUAN Xiaohui， JU Tingting， CHEN Jing

(School of Basic Science, Changchun University of Technology, Changchun 130012， China)

Three confidence interval estimationmethod for quantile regression model are introduced, which are direct method, bootstrap and induced smoothing method. The performance and the features of these methods for the confidence interval estimation are compared by simulation.

quantile regression; induced smoothing; bootstrap.

2016-11-21

吉林省科技廳青年科研基金資助項目(20150520055JH)

袁曉惠(1983-)，女,漢族，四川廣元人，長春工業大學講師,博士，主要從事缺失數據方向研究,E-mail:yuanxh@ccut.edu.cn.

10.15923/j.cnki.cn22-1382/t.2017.2.04

O 212.1

A

1674-1374(2017)02-0122-05