火星安全著陸軌跡快速生成的能控集法
葛丹桐,崔平遠,高 艾
(1. 北京理工大學宇航學院,北京100081;2. 深空自主導航與控制工信部重點實驗室,北京100081;3. 飛行器動力學與控制教育部重點實驗室,北京100081)
火星安全著陸軌跡快速生成的能控集法
葛丹桐1,2,3,崔平遠1,2,3,高 艾1,2,3
(1. 北京理工大學宇航學院,北京100081;2. 深空自主導航與控制工信部重點實驗室,北京100081;3. 飛行器動力學與控制教育部重點實驗室,北京100081)
針對火星著陸器在動力下降過程可能存在的著陸軌跡實時修正和著陸點再選擇等問題,本文通過離線計算著陸器在動力下降段開始時的能控集范圍,并在實際著陸過程中判斷著陸器當前狀態與能控集間的關系,實時確定最終著陸點并快速搜索相應著陸軌跡。若著陸器無法到達預定著陸點,則在視野范圍內根據安全因子重新選擇著陸點規劃運動軌跡。仿真表明,基于能控集的快速軌跡規劃法可根據著陸器的實際初始狀態快速確定最終著陸點并獲得相應著陸軌跡,以有限的燃耗實現火星安全軟著陸的目標。
火星動力下降;安全著陸;能控集;軌跡生成;安全因子
0 引 言
火星著陸探測是我國未來深空探測的主要目標,尤其是實現在具有科學價值地區的精確軟著陸,然而這樣的地區大多環境復雜、地形崎嶇[1-2],同時在整個著陸過程中還存在著系統累積誤差與環境擾動[3],所以對GNC系統提出了很高的要求。動力下降段作為著陸器著陸火星的最后階段,除了將下降速度減至零外,還需盡可能修正開傘點誤差以及傘漂所造成的與預定軌跡的位置偏差[4],以減小最終的著陸誤差,這一過程主要通過著陸器的橫向機動來實現[5]。由于實際過程中著陸器相對于標稱軌跡發生的偏移量難以提前準確估計,在轉移至目標著陸點時消耗的燃料有超出工程約束的風險[6]。因此在動力下降段開始時,需要結合著陸器當前狀態及能控范圍,確定最終著陸點[7]并快速搜索出相應著陸軌跡。當預定著陸點超出著陸器能控范圍時,則需在可見范圍內重新選取著陸點并在線規劃軌跡,以提高任務的成功率。
以上方法涉及到對著陸器能控集的離線計算與分析,能控集指能夠到達給定末端狀態的初始狀態集合,其概念最早產生于數學系統理論中,近些年,一些學者結合實際任務特點對其進行了改進并將之用于行星著陸探測研究中[8-9]。考慮到計算的復雜性,傳統的能控集分析多用于前期任務設計,并未考慮其在實際任務執行過程中的作用。同時,受制于星載機的計算與存儲能力,目前能夠在線生成的軌跡大多由形式簡單的解析制導律產生,如多項式制導[10]、能量最優制導[11]等,這些方法出于實時計算需求,只能滿足基本的約束如初始末端狀態約束,而在提前預判是否超出燃料上限以及提高安全著陸系統的靈活性等方面還有待進一步提高。
本文在分析速度增量的基礎上,得到火星動力下降段位置及速度能控集的快速生成方法,并將結果進一步用于下降過程中著陸軌跡的快速生成,為安全著陸的實現提供參考,其具體應用示意圖如圖1所示。
通過離線分析能控集,星載計算機可在實際下降過程中根據著陸器當前狀態與標稱值間的偏差大小,判斷其是否在提前存儲好的可控范圍內,實現以一定精度到達預定著陸點的目標,從而確定任務的最終著陸點,并進行軌跡的在線快速搜索。在極端情況下,假設目標著陸點及備用點均無法滿足需求,超出著陸器的控制范圍,則將重新在線規劃著陸點與著陸軌跡使任務得以繼續進行,從而提高著陸的安全性,實現行星表面的軟著陸。
1 下降段著陸模型
假設采用四條著陸腿著陸器,不能轉向的發動機固連在著陸器機體外側,指令推力矢量的方向通過改變著陸器姿態來實現,在理想情況下,發動機推力矢量方向能夠迅速機動到與制導加速度指令一致的方向上去,此外,由于目前對火星著陸器尚無滾轉要求,因此忽略推力矢量在滾轉方向的動力學。整個動力下降段動力學方程如下所示[12]
(1)
式中:(x,y,z)T為位置矢量,(u,v,w)T為速度矢量,Γ為比沖的大小,姿態角θ和ψ如圖2所示,表示了推力矢量在慣性系下的夾角。
采用好奇號任務在動力下降段使用的多項式制導方法,假設每個方向上的加速度都是時間的二次多項式[10]
a(t)=C0+C1t+C2t2
(2)
通過積分可得到速度和位置關于時間的函數。再結合初始和末端狀態約束即可解得相應系數。在下降過程中通過不斷測量當前狀態,并將測量結果輸入給制導模塊作為初始狀態,即可得到閉環的多項式制導律,其系數為
(3)
為了進一步得到下降時間,假設豎直方向加速度為關于時間的線性函數,即令C2z為0,同時假設rzf=vzf=azf=0,得到剩余時間表達式
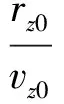
(4)
多項式制導形式簡單、計算方便,在需要大量存儲離線軌跡時,只需要存儲多項式的系數即可,免去了記錄每個節點狀態的巨大內存需求,為軌跡的在線快速搜索與生成提供了便利。參考“好奇號”任務,仿真所用到的著陸器相關參數如表1所示。
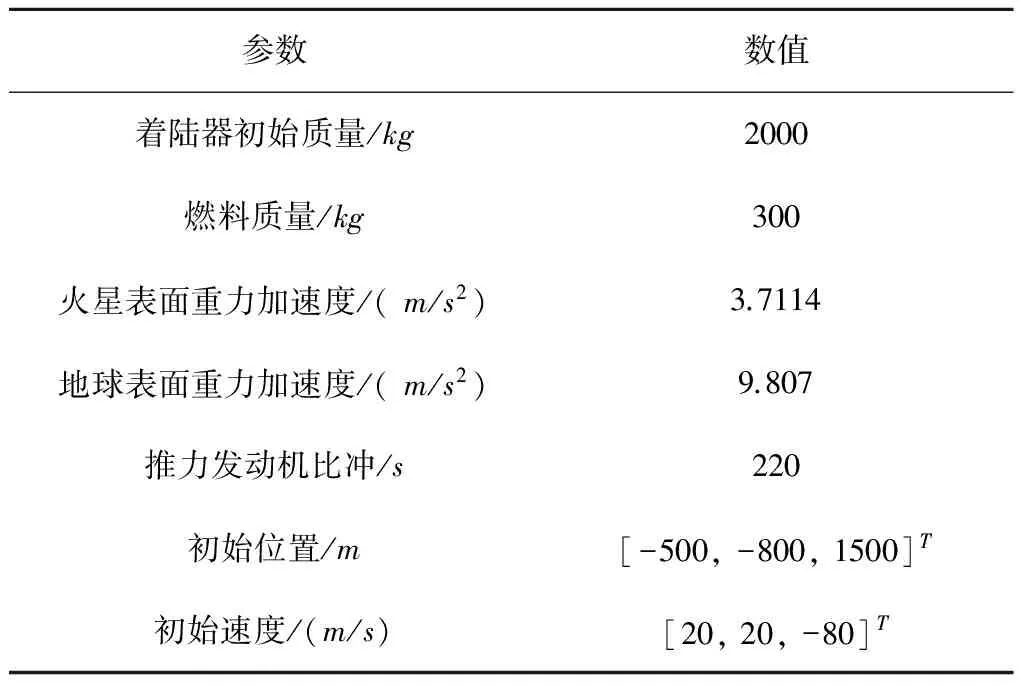
表1 仿真參數Table 1 Simulation parameters
2 速度增量計算
速度增量ΔV的大小表征了下降過程中著陸器為了減速所消耗的燃料多少。本節針對多項式制導方法,對速度增量表達式進行分析,得到著陸在不同位置的燃耗分布規律,從而避免了逐點積分計算著陸軌跡對應的燃耗,僅通過判斷著陸點所在區域即可快速得到相應軌跡的速度增量大小,為下降段能控集分析打下基礎。
給定目標著陸點,下降過程的速度增量可由下式計算得到[13]

(5)
式中:
(6)
(7)
即可得到兩個水平方向速度極值點對應的時刻,除了剩余時間tgo外,另一個解為
(8)
在每個水平方向,如果0 (9) (10) 由于tgo>0,故 (11) (12) (13) 聯立以上結果,關于時間的判斷條件轉化為關于空間的表達式 當vx0>0時, 當vx0≤0時, (14) 當vy0>0時, 當vy0≤0時, (15) 區域1和其他區域最大的區別在于該區域內的速度增量僅僅只取決于初始狀態,而在區域2~4中,速度增量是初始狀態和末端著陸點位置共同作用的結果。同時,隨著著陸點與中心點距離的增大,速度增量呈現出非線性變化特點。區域1的中心點為其邊界的平均值,即(rx0+1/3vx0tgo,ry0+1/3vy0tgo)。如圖4所示,在x-z平面存在以下幾何關系 (16) 代入式(4),上式可進一步轉化為 (17) 類似結果也可在y-z平面內得到。可以看出,區域1的中心點正是初始速度矢量與地表平面的交點,將中心點設為最終著陸點,著陸器將沿著初始位置與末端位置的連線飛行。 一般來說,任務在設計時會留有一定余量,使得著陸器在緊急情況如避障時仍有剩余燃料來實現機動[14],因此按照預定軌跡運動的著陸器所消耗的燃料便可以控制在合理范圍內。然而,由于傘降段無控制執行機構,開傘點誤差會經傳遞而不斷累積[15],當動力下降段開始時,著陸器的實際狀態可能會與預定值出現極大的偏差,為了實現精確軟著陸,著陸器需要在減速的同時橫向轉移很大的距離,以盡可能小的誤差著陸在目標著陸點附近,這一過程往往需要消耗大量的燃料,在極端情況下甚至有超出約束范圍的可能。因此分析動力下降段開始時的能控集,明確著陸器在有限燃耗下能夠到達給定目標著陸點的位置速度范圍,以進行在線著陸點確定和軌跡搜索或規劃就顯得尤為必要。 對于軟著陸任務,著陸器要實現的首要目標是以零速度安全降落在火星表面,因此末端著陸速度均設為0,根據表1中著陸器參數,得到所允許的最大速度增量[16]: (18) 著陸器若要實現在給定的燃料質量下以一定精度到達目標著陸點,動力下降段的初始位置不能距離著陸點太遠,速度也不能過大,為了定量描述能夠到達目標點的允許狀態范圍,本節分別針對動力下降段考察著陸器的位置能控集和速度能控集,并對于每個可行的狀態討論其對應軌跡的存儲方式。 表2 不同區域速度極值及速度增量表達式Table 2 Velocity extremum and velocity increment of different areas 3.1 能控集計算 在分析位置能控集時,僅考慮初始位置變化對速度增量的影響,固定初始速度與末端狀態為 v0=[20,20,-80]Tm/s 當初始位置改變時,對應軌跡的速度增量也會發生改變。根據上文的推導結果,針對每一個初始位置判斷目標著陸點位于哪個區域,并采用表2中相應區域的速度增量表達式對該軌跡對應的ΔV進行求解。將高度變化范圍設置為20m到2000m,對每一個高度分別進行計算,保留最大速度增量350m/s以內的區域,得到的初始位置能控集如圖5所示,圖中隨著高度的降低,位置能控集呈現出先增大后減小的趨勢,在大約1500m處達到最大。然而動力下降段的主要目的在于減速,其初始高度并不能無限降低到地表,這主要受發動機能夠提供最大推力的限制,過低的初始位置將嚴重影響有效減速高度,導致著陸器即使在燃耗范圍內始終以最大推力飛行也無法實現零速度著陸。考慮到多項式制導在豎直方向的加速度是關于時間的一次函數且末端值為0,因此其最大值出現在下降段的最開始,即 azmax=az0=az(t=0)=C0z= (19) (20) 因此最小的可行高度可由下式計算得到 (21) 類似方法同樣可以用于速度空間,得到相應的動力下降段初始速度可行域與沿標稱軌跡下降過程中的速度允許偏離范圍。具體來說,為了得到初始速度可行域,首先固定初始位置與末端狀態 r0=[-500,-800,1500]Tm 接著針對每一個初始速度判斷目標著陸點位于哪個區域,并用相應區域的速度增量表達式對ΔV進行求解。將下降速度變化范圍設置為-50m/s到-100m/s,對每個下降速度分別進行計算,保留最大速度增量350m/s以內的區域,得到的初始速度能控集如圖6所示,圖中隨著下降速度的減小,速度能控集不斷縮小。 3.2 軌跡簇離線存儲 類似地,當有多個備選著陸點時,可依次得到每個著陸點對應的能控集范圍,這些能控集的并集表明了在動力下降段開始時由系統誤差及外界干擾造成的著陸器相對于標稱狀態的允許偏離范圍。能控并集中每一個狀態量對應一條滿足工程約束的著陸軌跡,通過離線計算并存儲這些軌跡,可實現著陸器星上軌跡實時快速搜索,從而減少了在線計算量與生成軌跡所需要的時間。同時,由于多項式制導形式簡單,位置與速度均為關于時間的多項式函數,因此只需要存儲多項式的系數即可得到相應的著陸軌跡,對內存的需求也大大降低,對于非多項式形式的制導方法,可采取存儲軌跡節點的方式以降低存儲需求。 不失一般性,以下假設初始速度已知,僅考慮位置能控并集及其對應的軌跡簇。假設提前選取的三個預定著陸點X,Y,Z,其坐標分別為rX=[0,0,0]Tm、rY=[1000,500,0]Tm、rZ=[-1000,-1000,0]Tm,考慮科學價值、工程約束等因素,其按優先級排序為X→Y→Z,即X為目標著陸點,Y、Z為備選點。根據第3.1節分別計算著陸點X、Y、Z在高度為1500m處對應的橫向初始位置能控集,得到的結果如圖7所示。 注意到三個著陸點在同一高度的初始位置能控集出現了交叉重疊的情況,當著陸器實際位置落在重疊區域時,根據優先級順序選取著陸點。將能控并集每個點的位置信息與對應軌跡的多項式系數以及相應著陸點優先級順序按照以下方式存儲在矩陣M中 在線判斷著陸器當前狀態與提前存儲的能控集間的關系存在兩種結果:若著陸器狀態位于能控集范圍內,意味著著陸器能夠利用有限燃耗到達預定的目標著陸點,此時僅需要搜索出符合當前狀態的軌跡參數,即可得到下降軌跡;若著陸器無法到達預定著陸點,即著陸器狀態由于系統誤差或外界擾動影響超出能控集時,系統需要根據當前情況實時在線規劃出新的著陸點與著陸軌跡,在不違背工程約束的前提下實現著陸器的安全著陸。 4.1 在能控集范圍內 Ck0=[1.6593,7.3481,2.8444]T 則相應的制導律與軌跡為 (22) 相應的加速度及位置變化曲線如圖8~9所示,著陸器通過在線控制推力器推力大小,使其沿生成的軌跡運動,即可保證在有限燃耗的情況下到達目標著陸點。 4.2 超出能控集范圍 當著陸系統根據敏感器信息判斷出著陸器位于能控集范圍外,意味著即使消耗盡所有的燃料也無法將著陸器送至預定目標點時,系統需要對可行的著陸點進行快速重新評估,并根據當前狀態與新選取出的著陸點在線生成著陸軌跡。 假設下降段初始位置r0=[3000,-800,1500]Tm,由圖7可知,此時無論到達哪個目標著陸點消耗的燃料都將超出著陸器的最大轉移能力,因此需要在線對視野范圍內的地形進行快速評估,使得著陸器利用有限燃耗降落在安全的地方[17]。考慮在以目標著陸點為中心的6000m×6000m地形范圍內,結合著陸器初始狀態,分別以每個像素點作為著陸點計算各點速度增量,剔除高于最大速度增量350 m/s的區域,對剩余的地形區域進行測量篩選,利用敏感器信息重建地形,得到行星表面DEM信息,如圖10所示,其中深色部分為視野范圍內不可達區域,淺色部分為提取的可行區域。 根據得到的DEM信息計算可行區域內各點的坡度φ和表面粗糙度dl[18],結合著陸器能夠容忍的障礙尺寸如巖石高度、坡度大小等約束,利用文獻[19]提出的安全因子概念以及基于安全因子的著陸點評估方法,通過以下簡化的地形安全評分標準對該區域各點進行安全性評估,從而得到最適宜著陸的地區 (23) 假設ηφ=ηd=0.5,φsafe=15°,dsafe=0.5m,不失一般性,不可達區域的安全評分此處取S(xi,yi)=20,將計算結果按安全評分高低進行排序,評分越低意味著對應區域越安全,得到的新著陸點rf=[1730,-1870,0]Tm(即全局最小值所在位置)如圖11所示。此后著陸器再根據當前狀態與新的末端狀態利用多項式制導重新生成軌跡,得到多項式系數 C0=[-6.9499,-6.1914,2.8444]T 相應的加速度及位置變化曲線如圖12~13所示。同理,當著陸器沿該軌跡運動時,可實現有限燃耗下的安全著陸。 另外,盡管傳統的多項式制導可在下降過程中實現實時燃耗估計并更新著陸點,但這一過程往往涉及到對著陸器的機動范圍進行在線分析與評估,對星載機的計算速率提出了很高的要求;而本文提出的方法其主要優勢體現在可提前離線完成著陸器到達不同備選著陸點的燃耗評估預測,以盡可能減少在線運算量為目標,給出了一套快速搜索生成軌跡的方法,從而在不增加星載機計算量的前提下提高了任務的安全性。 火星動力下降過程中著陸器為了消除橫向偏差,往往需要進行大范圍的橫向轉移,這對其所攜帶的有限燃料提出了挑戰。為提高火星著陸的安全性,本文在離線分析著陸器到達不同著陸點的速度增量分布規律的基礎上,結合工程參數,提前計算出動力下降段的初始狀態能控集范圍,并將其與對應的軌跡參數進行存儲。在實際飛行過程中,著陸器通過判斷當前狀態與存儲的能控集間的關系以確定最終著陸點及相應下降軌跡:當著陸器狀態位于能控集中時,通過在提前存儲的矩陣中進行一維線性搜索得到最終著陸點坐標及相應軌跡多項式系數;當著陸器狀態位于能控集外時,則需要在線根據地形安全評價標準——安全因子重新選取著陸點,快速進行軌跡重規劃,以保證著陸器在有限燃耗下著陸在安全的地形表面。仿真結果表明,基于能控集的快速軌跡規劃法能夠在下降過程中快速確定最終著陸點并生成下降軌跡,可實現著陸器在初始狀態無法提前準確預知情況下的安全著陸,從而提高了著陸器的自主性與任務的成功率。 本文以多項式制導為例,給出了軌跡快速生成能控集法的具體應用。相比于更為復雜的難以實現實時在線計算的制導方法,本文方法對在線確定著陸點并快速生成軌跡將更具有優越性。未來可圍繞更為先進的制導方法(如凸優化等)研究不同制導律下的軌跡快速生成策略,為安全著陸系統軌跡設計提供參考。 [1] 崔平遠, 胡海靜, 朱圣英. 火星精確著陸制導問題分析與展望[J]. 宇航學報, 2014, 35(3):245-253. [Cui Ping-yuan, Hu Hai-jing, Zhu Sheng-ying. Analysis and prospect of guidance aspects for Mars precision landing[J]. Journal of Astronautics, 2014, 35(3):245-253.] [2] Epp C D, Robertson E A, Carson J M. Real-time hazard detection and avoidance demonstration for a planetary lander[C]. AIAA SPACE 2014 Conference and Exposition, San Diego, USA, August 4-7, 2014. [3] 于正湜, 崔平遠. 行星著陸自主導航與制導控制研究現狀與趨勢[J]. 深空探測學報, 2016, 3(4):345-355. [Yu Zheng-shi, Cui Ping-yuan. Research status and developing trend of the autonomous navigation, guidance, and control for planetary landing[J]. Journal of Deep Space Exploration, 2016, 3(4): 345-355.] [4] 任高峰, 高艾, 崔平遠,等. 一種燃料最省的火星精確著陸動力下降段快速軌跡優化方法[J]. 宇航學報, 2014, 35(12):1350-1358. [Ren Gao-feng, Gao Ai, Cui Ping-yuan,et al. A rapid power descent phase trajectory optimization method with minimum fuel consumption for Mars pinpoint landing[J]. Journal of Astronautics, 2014, 35(12):1350-1358.] [5] Harris M W, A?1kmee B. Maximum divert for planetary landing using convex optimization[J]. Journal of Optimization Theory and Applications, 2014, 162(3):975-995. [6] Dueri D, A?1kmee B, Scharf D P, et al. Customized real-time interior-point methods for onboard powered-descent guidance[J]. Journal of Guidance Control & Dynamics, 2017, 40(2):197-212. [7] 田陽, 崔平遠, 崔祜濤. 基于圖像的著陸點評估及著陸器運動估計方法[J]. 宇航學報, 2010, 31(1):98-103. [Tian Yang, Cui Ping-yuan, Cui Hu-tao. Landing site assessment and probe motion estimation based on image[J]. Journal of Astronautics, 2010, 31(1):98-103.] [8] Eren U, Dueri D, A?1kmee B. Constrained reachability and controllability sets for planetary precision landing via convex optimization[J]. Journal of Guidance Control & Dynamics, 2015, 38(11):1-17. [9] Long J, Gao A, Cui P. Controllable set analysis for planetary landing under model uncertainties[J]. Advances in Space Research, 2015, 33(2):281-292. [10] Steinfeldt B A, Grant M J, Matz D A, et al. Guidance, navigation, and control system performance trades for Mars pinpoint landing[J]. Journal of Spacecraft & Rockets, 2012, 47(1):188-198. [11] D’Souza C. An optimal guidance law for planetary landing[C]. AIAA Guidance, Navigation, and Control Conference, 1997. [12] Topcu U, Casoliva J, Mease K D. Minimum-fuel powered descent for Mars pinpoint landing[J]. Journal of Spacecraft & Rockets, 2007, 44(2):324-331. [13] Wong E C, Singh G, Masciarelli J P. Guidance and control design for hazard avoidance and safe landing on Mars[J]. Journal of Spacecraft & Rockets, 2015, 43(2):378-384. [14] 王大軼, 李驥, 黃翔宇,等. 月球軟著陸過程高精度自主導航避障方法[J]. 深空探測學報, 2014, 1(1):44-51. [Wang Da-Ji, Li Ji, Huang Xiang-yu, et al. A pinpoint autonomous navigation and hazard avoidance method for lunar soft landing[J]. Journal of Deep Space Exploration, 2014, 1(1):44-51.] [15] Quadrelli M B, Wood L J, Riedel J E, et al. Guidance navigation and control technology assessment for future planetary science missions[J]. Journal of Guidance Control & Dynamics, 2015, 38(7):1165-1186. [16] Ploen S R, Seraji H, Kinney C E. Determination of Spacecraft landing footprint for safe planetary landing[J]. Aerospace & Electronic Systems IEEE Transactions on, 2009, 45(1):3-16. [17] 崔平遠, 葛丹桐. 一種行星安全著陸點綜合評估方法[J]. 深空探測學報, 2016, 3(4):363-369. [Cui Ping-yuan, Ge Dan-tong. An integrated evaluation of planetary safe landing site[J]. Journal of Deep Space Exploration, 2016, 3(4):363-369.] [18] 吳偉仁, 王大軼, 黃翔宇,等. 月球軟著陸自主障礙識別與避障制導方法[J]. 中國科學:信息科學, 2015, 45(8):1046-1059. [Wu Wei-ren, Wang Da-yi, Huang Xiang-yu, et al. Autonomous hazard detection and avoidance guidance method for soft lunar landing[J]. Scientia Sinica Informationis, 2015, 45(8):1046-1059.] [19] Cui P, Ge D, Gao A. Optimal landing site selection based on safety index during planetary descent[J]. Acta Astronautica, 2017, 132: 326-336. 通信地址:北京市海淀區中關村南大街5號北京理工大學宇航學院(100081) 電話:(010)68918910 E-mail: gedt@bit.edu.cn 崔平遠(1961-),男,教授,博士生導師,主要從事飛行器自主導航與控制、深空著陸器自主技術與軌道設計。本文通信作者。 通信地址:北京市海淀區中關村南大街5號北京理工大學宇航學院(100081) 電話:(010)68918611 E-mail: cuipy@bit.edu.cn (編輯:牛苗苗) Rapid Generation of Mars Safe Landing Trajectory Based on Reachability Set GE Dan-tong1,2,3, CUI Ping-yuan1,2,3, GAO Ai1,2,3 (1. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China; 2. Key Laboratory of Autonomous Navigation and Control for Deep Space Exploration, Ministry of Industry and Information Technology, Beijing 100081, China; 3. Key Laboratory of Dynamics and Control of Flight Vehicle, Ministry of Education, Beijing 100081, China) To solve the problems of possible real-time trajectory correcting and landing site re-designating during Mars powered descent, the paper computes the reachability set at the beginning of the powered descent phase offline and determines the final landing site online by comparing the current state of the lander with the obtained reachability set. The corresponding descent trajectory is then rapidly searched. If the lander fails to reach any of the given targets, a new landing site in the field of view will be selected through safety index and a trajectory will be planned. The simulation result shows that the proposed reachability set-based rapid trajectory planning method manages to determine the final landing site and obtain the landing trajectory in real-time according to the practical initial state of the lander, fulfilling the goal of Mars soft landing with limited fuel consumption. Mars powered descent; Safe landing; Reachability set; Trajectory generation; Safety index 2017-03-06; 2017-03-31 國家自然科學基金(61374216, 61304226, 61304248, 61603039);中國博士后科學基金(2016M591087) V448.2 A 1000-1328(2017)05-0497-09 10.3873/j.issn.1000-1328.2017.05.008 葛丹桐(1992-),女,博士生,主要從事行星探測制導與控制、安全著陸與障礙規避。
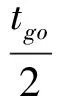
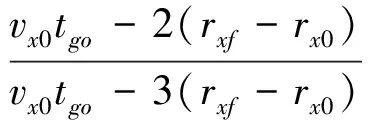
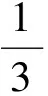
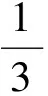
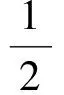
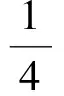
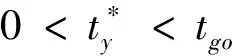
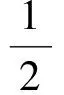
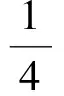
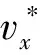

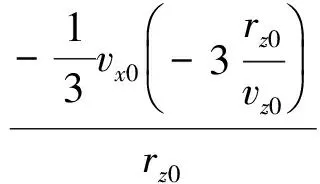
3 能控集分析及離線軌跡存儲

rf=[0,0,0]Tm
vf=[0,0,0]Tm/s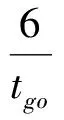
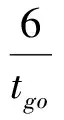
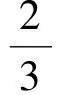
rf=[0,0,0]Tm
vf=[0,0,0]Tm/s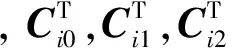
4 軌跡在線快速生成方法
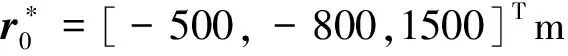
Ck1=[-0.1559,-0.5605,-0.0506]T
Ck2=[0.0022,0.0076,0]T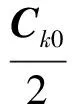
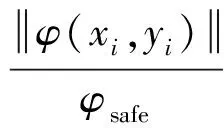
C1=[0.4563,0.4024,-0.0506]T
C2=[-0.0059,-0.0052,0]T5 結 論

