面向剛?cè)狁詈闲l(wèi)星的有限時間輸出反饋姿態(tài)控制

肖 巖，葉 東，孫兆偉

(哈爾濱工業(yè)大學(xué)航天學(xué)院，哈爾濱150001)

面向剛?cè)狁詈闲l(wèi)星的有限時間輸出反饋姿態(tài)控制

肖 巖，葉 東，孫兆偉

(哈爾濱工業(yè)大學(xué)航天學(xué)院，哈爾濱150001)

針對進行大角度快速機動的剛?cè)狁詈闲l(wèi)星，提出了有限時間控制方法。首先在考慮衛(wèi)星本體運動與柔性附件變形耦合效應(yīng)的情況下，建立一次近似剛?cè)狁詈蟿恿W(xué)模型。其次假設(shè)柔性附件振動信息可測，考慮外部干擾和轉(zhuǎn)動慣量不確定性，基于非奇異快速終端滑模(NFTSM)原理，設(shè)計了有限時間全狀態(tài)反饋控制器，根據(jù)Lyapunov原理證明其有限時間穩(wěn)定性；進一步考慮柔性附件振動信息不可測的實際情況，設(shè)計了非奇異快速終端滑模動態(tài)輸出反饋控制器，該控制器僅利用角度和角速度信息就可以實現(xiàn)有限時間快速姿態(tài)穩(wěn)定。最后對提出的控制算法進行了數(shù)值仿真，并通過與現(xiàn)有文獻中控制算法進行對比，驗證了本文設(shè)計的輸出反饋控制算法的有限時間快速穩(wěn)定特性。

剛?cè)狁詈闲l(wèi)星；快速機動；姿態(tài)控制；有限時間控制；終端滑模；輸出反饋

0 引 言

為了減輕發(fā)射重量，控制發(fā)射成本，完成特定的在軌任務(wù)，柔性附件在現(xiàn)代衛(wèi)星上的應(yīng)用越來越普遍，如通信衛(wèi)星上的太陽能帆板，遙感衛(wèi)星上的大型柔性天線，在軌服務(wù)衛(wèi)星上的大型柔性機械臂等[1]。由于柔性附件本身的結(jié)構(gòu)特點，如低模態(tài)頻率，弱阻尼等，衛(wèi)星在軌的姿態(tài)機動必然會引起柔性附件的振動，柔性附件振動和中心剛體運動相耦合，會極大地降低衛(wèi)星在軌姿態(tài)控制的精度[2]。此外，復(fù)雜的航天任務(wù)要求衛(wèi)星在軌具有大角度快速機動能力，比如遙感衛(wèi)星成像過程中在多目標(biāo)之間的切換，偵察衛(wèi)星對空間目標(biāo)的捕獲等。在大角度快速機動情況下，剛?cè)狁詈咸匦詴用黠@，所以就更加不能忽略其對姿態(tài)控制的影響[3-4]。

針對柔性衛(wèi)星的控制問題，一些文獻進行了相關(guān)的研究。文獻[5]結(jié)合模糊機制和滑模控制，針對三軸柔性衛(wèi)星設(shè)計了姿態(tài)機動控制器，達到了姿態(tài)的漸近穩(wěn)定。文獻[6]針對剛?cè)狁詈闲l(wèi)星，基于Lyapunov方法設(shè)計了姿態(tài)反饋調(diào)節(jié)控制器，控制過程中考慮了外在干擾，姿態(tài)角和角速度可以漸近收斂，柔性附件的振動也達到了衰減。文獻[7]針對柔性衛(wèi)星，在撓性模態(tài)不可測的情況下，設(shè)計了混合H2 /H∞ 輸出反饋姿態(tài)控制器，在達到姿態(tài)穩(wěn)定的同時，減小了撓性振動模態(tài)。針對噴氣控制且柔性附件安裝有撓性應(yīng)變片的三軸穩(wěn)定柔性衛(wèi)星，文獻[8]設(shè)計了自適應(yīng)滑模姿態(tài)調(diào)節(jié)控制器，并基于線性二次調(diào)節(jié)設(shè)計了正位置反饋主動振動抑制機制，達到了姿態(tài)漸近穩(wěn)定。文獻[9]針對柔性衛(wèi)星設(shè)計了滑模姿態(tài)機動控制器。首先對姿態(tài)機動中的角速度進行規(guī)劃，減少對柔性附件振動的激發(fā)；然后基于冪次趨近律設(shè)計了滑模控制律，在達到姿態(tài)穩(wěn)定的同時，有效抑制了抖振。文獻[10]針對柔性衛(wèi)星，設(shè)計了無角速度情況下的姿態(tài)機動控制器，使用擴展?fàn)顟B(tài)觀測器對角速度和系統(tǒng)總干擾進行了估計，最后設(shè)計了姿態(tài)反饋控制器達到了漸近穩(wěn)定。上述針對柔性衛(wèi)星進行設(shè)計的姿態(tài)控制器只能保證柔性衛(wèi)星姿態(tài)漸近穩(wěn)定，其收斂時間理論上是無限的，往往并不能滿足快速機動的要求。

有限時間姿態(tài)控制穩(wěn)定時間是有限的，相比于無限穩(wěn)定時間的控制器，具有快速穩(wěn)定的優(yōu)勢。此外，由于有限時間控制方法中引入了分數(shù)次冪，所以還具有更好的魯棒性和抗干擾特性。針對有限時間姿態(tài)控制，許多文獻進行了相關(guān)的研究。文獻[11]針對單個剛體航天器設(shè)計了有限時間姿態(tài)跟蹤控制器，在此基礎(chǔ)上針對多個航天器設(shè)計了有限時間姿態(tài)協(xié)同控制器。針對四元數(shù)表示的剛體航天器動力學(xué)模型，文獻[12]設(shè)計了有限時間終端滑模控制器，使用自適應(yīng)方法對外在干擾進行了估計。文獻[13]在考慮模型不確定性和外部干擾上界未知的情況，針對剛體衛(wèi)星設(shè)計了非奇異快速終端滑模控制器，通過自適應(yīng)方法對控制器增益進行了估計，該控制器在保持有限時間收斂的同時，具有更快的收斂速度，而且還避免了奇異。文獻[14]引入了擴展?fàn)顟B(tài)觀測器對系統(tǒng)總擾動進行了估計，在將估計值進行反饋補償?shù)幕A(chǔ)上設(shè)計了非奇異快速終端滑模跟蹤控制器，使得衛(wèi)星姿態(tài)可以有限時間收斂。文獻[15]針對剛體航天器設(shè)計了有限時間非奇異快速終端滑模控制器，在模型不確定性以及外界干擾上界未知的情況下引入自適應(yīng)估計策略，由于該控制器是連續(xù)的，所以明顯削弱了抖振，最后基于Hubble望遠鏡的數(shù)值仿真驗證了控制器的有效性。

根據(jù)對以上相關(guān)文獻的研究發(fā)現(xiàn)，雖然一部分文獻針對衛(wèi)星進行了有限時間姿態(tài)控制的研究，但是沒有考慮柔性附件對衛(wèi)星姿態(tài)控制帶來的影響。同樣針對柔性衛(wèi)星的姿態(tài)控制，一部分文獻設(shè)計了穩(wěn)定的控制器，使得柔性衛(wèi)星姿態(tài)漸近穩(wěn)定，但是均不能達到有限時間快速穩(wěn)定。在此研究背景下，本文針對大角度快速機動的柔性衛(wèi)星，進行了有限時間快速姿態(tài)控制研究。與現(xiàn)有文獻相比，本文在動力學(xué)建模過程中，充分考慮了柔性附件振動與中心剛體運動之間的剛?cè)狁詈闲?yīng)。在此基礎(chǔ)上設(shè)計了有限時間快速穩(wěn)定控制器，使得柔性衛(wèi)星姿態(tài)可以達到有限時間快速穩(wěn)定。

本文在考慮外部干擾和模型不確定性的情況下，研究了剛?cè)狁詈闲l(wèi)星的有限時間輸出反饋控制方法。文章安排如下： 第1節(jié)基于一次近似耦合方法建立了剛?cè)狁詈蟿恿W(xué)模型。第2節(jié)基于非奇異快速終端滑模原理，設(shè)計了有限時間狀態(tài)反饋控制器,并且進一步考慮柔性附件振動不可測的情況，設(shè)計了僅利用姿態(tài)和角速度信息的有限時間輸出反饋控制器。第3節(jié)利用數(shù)值仿真驗證了控制器的有效性。第4節(jié)為結(jié)論。

1 一次近似剛?cè)狁詈蟿恿W(xué)模型

為提高大角度快速機動背景下的剛?cè)狁詈闲l(wèi)星建模精度，本節(jié)基于一次近似耦合建模方法，建立了柔性衛(wèi)星一次近似剛?cè)狁詈蟿恿W(xué)模型。與傳統(tǒng)的線性模型和零次近似剛?cè)狁詈夏Ｐ拖啾龋疚慕⒌哪Ｐ驮谧冃挝灰茍鲋幸肓藱M向變形與軸向伸長的二次耦合項，充分反應(yīng)了柔性附件變形與中心剛體轉(zhuǎn)動之間的耦合效應(yīng)，在大角度快速機動情況下更為精確。

如圖1為帶有柔性附件的剛?cè)狁詈闲l(wèi)星模型俯視圖，中心圓柱體為剛體，柔性附件固聯(lián)于剛體表面。柔性附件為細長梁，忽略剪切與扭轉(zhuǎn)形變。梁在水平面內(nèi)運動，忽略重力效應(yīng)，梁自由端固聯(lián)有質(zhì)量塊。坐標(biāo)系OXY為原點位于中心剛體球心的慣性坐標(biāo)系，坐標(biāo)系ORxy為原點位于柔性梁連接點，x軸沿未變形梁的參考坐標(biāo)系。

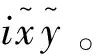
依據(jù)有限元法和Hamilton最小作用原理[16-18]，建立一次近似剛?cè)狁詈蟿恿W(xué)方程如下

(1)

(2)

其中

GT=G=Dr-Ms>0

式中：θ為中心剛體轉(zhuǎn)角；JH、JA、JT分別為中心剛體、柔性附件和末端質(zhì)量塊相對于轉(zhuǎn)軸的轉(zhuǎn)動慣量；Tc為控制力矩，Td為外部干擾力矩；Ms、Ks分別為柔性梁結(jié)構(gòu)質(zhì)量矩陣和結(jié)構(gòu)剛度矩陣，均為對稱正定矩陣；對稱正定矩陣Dr為柔性梁轉(zhuǎn)動剛度陣，且Dr-Ms滿足正定對稱條件；Cs=b1Ms+b2Ks為根據(jù)Rayleigh比例阻尼設(shè)計的系統(tǒng)結(jié)構(gòu)阻尼矩陣，b1、b2為大于0的系數(shù)；U為剛?cè)狁詈舷禂?shù)矩陣。

(3)

(4)

(5)

其中

其中,F為剛?cè)狁詈蠀?shù)，H為包含柔性變量的柔性部分。將高階剛?cè)狁詈享椏醋鞲蓴_，TD為包含高階剛?cè)狁詈享椀南到y(tǒng)干擾。

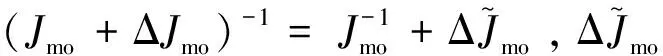
(6)

其中：

式中：ΔM為轉(zhuǎn)動慣量不確定引起的模型未知項，g為外部干擾項。

2 非奇異快速終端滑模控制器設(shè)計

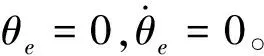
2.1 有限時間控制

為方便后文控制器設(shè)計，給出有限時間穩(wěn)定相關(guān)定義和引理。

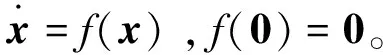
1)V為正定函數(shù)；

2)存在正實數(shù)α>0,1>p>0，以及一個不包含原點的開鄰域D0?D，使得函數(shù)V滿足

(7)

那么系統(tǒng)為有限時間穩(wěn)定，且收斂時間為

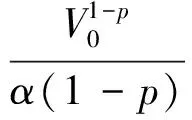
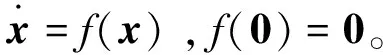
1)V為正定函數(shù)；

2)存在正實數(shù)α>0,β>0,1>p>0，以及一個不包含原點的開鄰域D0?D，使得函數(shù)V滿足

(8)

那么系統(tǒng)為快速有限時間穩(wěn)定，且收斂時間為

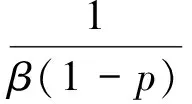
在控制器設(shè)計過程中，大多數(shù)情況并不需要系統(tǒng)軌跡在有限時間內(nèi)嚴(yán)格收斂于零，而只需要穩(wěn)定于滿足設(shè)計需要的一個小鄰域，為此，有的學(xué)者提出了更適用的實際有限時間穩(wěn)定(Practical finite-time stable，PFS)[21]。

2.2 非奇異快速終端滑模

將誤差動力學(xué)方程，改寫為狀態(tài)空間形式：

(9)

(10)

其中

式中：d=Jmog+JmoΔM為包含高階剛?cè)狁詈享棥⒏蓴_力矩以及轉(zhuǎn)動慣量不確定項的系統(tǒng)總干擾。

針對一次近似剛?cè)狁詈蟿恿W(xué)模型，傳統(tǒng)的線性滑模面可以設(shè)計如下

(11)

其中,k>0，系統(tǒng)軌跡在到達滑模面后，只能漸近收斂到零點。

終端滑模在傳統(tǒng)線性滑模面的基礎(chǔ)上引入了非線性項，從而使系統(tǒng)軌跡可以沿滑模面在有限時間內(nèi)收斂到零點，具體設(shè)計如下

(12)

(13)

式中：k,k1>0，0<γ<1。由上式可知系統(tǒng)軌跡在遠離零點的時候，由線性項k1θe提供更快的收斂速度，當(dāng)系統(tǒng)軌跡接近零點的時候，由收斂速度更快的非線性項ksig(θe)γ作為主導(dǎo)，所以系統(tǒng)軌跡在全局都能快速收斂。

對快速終端滑模求導(dǎo)得

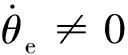
(14)

式中：a,b>0,2>γ2>1，且γ1>γ2。對非奇異快速終端滑模函數(shù)求導(dǎo)得

(15)

由于γ1-1>0，γ2-1>0，非奇異快速終端滑模可以有效避免奇異。

2.3 狀態(tài)反饋控制器設(shè)計

采用式(14)表示的非奇異快速終端滑模面，將動力學(xué)方程(9)代入式(15)得

(16)

假設(shè)1. 存在非負函數(shù)L(θ,p,χ,t)，滿足

由于角度、角速度是有界的，高階剛?cè)狁詈享棥⑼獠扛蓴_和轉(zhuǎn)動慣量不確定性與控制力矩相比是小值，易知d是有界的，所以假設(shè)1是合理的。

在姿態(tài)信息和柔性附件振動信息均可測情況下，根據(jù)終端滑模控制器設(shè)計原理，設(shè)計如下狀態(tài)反饋控制器

Tc=Teq+Tvss

(17)

(18)

Tvss=-(λ+L(θ,p,χ,t))sgn(s)

(19)

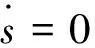
定理1. 針對存在干擾和模型不確定性的衛(wèi)星動力學(xué)系統(tǒng)(9)、(10)，存在控制器(17)～(19)，使得系統(tǒng)軌跡在有限時間內(nèi)收斂到零點。

證. 設(shè)Lyapunov函數(shù)為

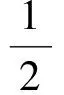
(20)

對上式求導(dǎo)，并將控制器(17)～(19)代入得

L(θ,p,χ,t))sign(s)))≤

(21)

(22)

在滿足滑模到達條件后，系統(tǒng)軌線到達滑模面s=0，即

(23)

(24)

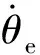
證畢。

2.4 動態(tài)輸出反饋控制器設(shè)計

在實際的在軌任務(wù)中，柔性附件的振動信息很難進行測量或進行精確實時測量，所以將柔性附件的節(jié)點坐標(biāo)信息當(dāng)作系統(tǒng)狀態(tài)進行反饋控制在通常情況下很難實現(xiàn)。針對這一問題，本節(jié)在狀態(tài)反饋控制器的基礎(chǔ)上設(shè)計輸出反饋控制器，僅利用角度和角速度信息來達到系統(tǒng)的有限時間穩(wěn)定。

采用非奇異快速終端滑模面(14)，基于假設(shè)1以及姿態(tài)角和姿態(tài)角速度信息，設(shè)計動態(tài)輸出反饋控制器如下：

(25)

(26)

式中：

控制器切換增益λ和λ1為常數(shù)，且滿足λ>0,λ1>1。Γ為正定對角的觀測增益矩陣，基于柔性附件具有非負慣性阻尼的假設(shè),可知存在Γ滿足ΓA<0。

定理2. 針對存在干擾和模型不確定性的衛(wèi)星動力學(xué)系統(tǒng)(9)、(10)，存在控制器(25)、(26)，使得s、ep和eχ一致最終有界。

證. 選取Lyapunov函數(shù)如下

(27)

對式(27)求導(dǎo)，并將控制器(25)、(26)代入得

(λ+L(θ,p,χ,t))sgn(s)-λ1s))≤

(28)

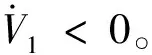
證畢。

通過式(28)的證明，可以知道s、ep和eχ是一致最終有界的，但是這并不能說明衛(wèi)星姿態(tài)可以在有限時間收斂[25]。設(shè)

(29)

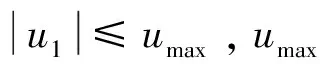
定理3. 針對柔性衛(wèi)星剛?cè)狁詈险`差動力學(xué)方程(9)、(10)，存在控制器(25)、(26)，當(dāng)初始條件滿足

(30)

其中,Vmax>0，滑模面s可在有限時間到達鄰域

(31)

(32)

(33)

(34)

證. 設(shè)Lyapunov函數(shù)

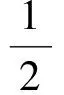
(35)

對Lyapunov函數(shù)進行求導(dǎo)，并將控制力矩代入整理得

(λ+L(θ,p,χ,t))sgn(s)-λ1s))≤

-φb1V-φb2V1/2+φc

(36)

式(36)推導(dǎo)過程中用到了如下不等式關(guān)系

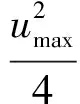
(37)

(38)

當(dāng)b1-c/V>0時，由引理2可知式(37)符合快速有限時間穩(wěn)定形式，則滑動模態(tài)s可在有限時間內(nèi)收斂到區(qū)域

(39)

當(dāng)b2-c/V1/2>0時，式(38)符合快速有限時間穩(wěn)定形式，則滑動模態(tài)s可在有限時間內(nèi)收斂到區(qū)域

(40)

(41)

上式可整理為如下兩種形式

(42)

(43)

(44)

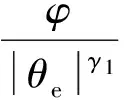
(45)

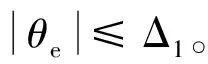
(46)

證畢。

3 仿真結(jié)果與分析

本節(jié)主要對文中提出的狀態(tài)反饋控制器(17)～(19)和動態(tài)輸出反饋控制器(25)、(26)進行數(shù)值仿真以驗證其有效性，并與文獻[6]中設(shè)計的自適應(yīng)輸出反饋控制器進行對比。其中柔性衛(wèi)星參數(shù)采用文獻[18]中給出的參數(shù)。

3.1 狀態(tài)反饋控制

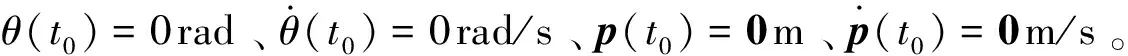
從圖2可以看出，針對姿態(tài)角控制，控制器(17)～(19)可在25s收斂，并在32s達到5×10-6rad控制精度，同樣從圖3可以看出，本文提出的控制器可在20s使得姿態(tài)角速度收斂到小值，并在30s達到2.5×10-6rad/s控制精度，由圖4可知，撓性附件末端初期振動較大，但是振動可以快速衰減。由圖5的仿真結(jié)果可以看出，本文的控制力矩存在微弱抖振現(xiàn)象，這是由于控制器中存在不連續(xù)的符號函數(shù)導(dǎo)致，與理論分析相一致。

3.2 動態(tài)輸出反饋控制

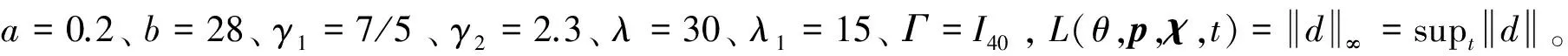
分析仿真結(jié)果可知，在柔性信息不可測的情況下，本文設(shè)計的動態(tài)輸出反饋控制器可以使得誤差姿態(tài)角和姿態(tài)角速度有限時間快速收斂，由于柔性信息估計誤差的存在，控制精度有所下降，但是仍然滿足要求。由于在柔性信息估計過程中引入了滑模變量，從圖10～11可以看出，估計值與真實值相比，振動頻率更大，但是誤差值快速收斂，可以提供控制器設(shè)計所需精度的柔性信息。

針對姿態(tài)角控制，由圖6可知，相比于文獻[6]中的自適應(yīng)控制器，控制器、可在35s達到5×10-6rad控制精度，而文獻中的自適應(yīng)控制器直到120s才達到穩(wěn)定，雖然穩(wěn)態(tài)精度比本文的控制器精度高，但是均處于同一數(shù)量級，相差并不大。同樣從圖7可以看出，本文提出的控制器可在30s使得姿態(tài)角速度達到2×10-5rad/s控制精度，而文獻[6]中的控制器直到80s才可穩(wěn)定，穩(wěn)態(tài)精度為1×10-5rad/s。對于需要完成大角度快速機動的剛?cè)狁詈闲l(wèi)星來說，本文提出的控制器在收斂時間上有明顯優(yōu)勢，而且穩(wěn)態(tài)精度也滿足在軌任務(wù)的要求。從圖9可以看出，與文獻[6]相比，本文控制器飽和階段更短，且衰減更快。從圖8可以看出，撓性附件末端振動與文獻[6]相比，雖然初期振動要稍大，但是更早開始衰減，且衰減速度更快。所以在考慮柔性附件振動的情況下，本文設(shè)計的控制器也具有優(yōu)勢。

4 結(jié) 論

本文研究了大角度快速機動情況下剛?cè)狁詈闲l(wèi)星的有限時間姿態(tài)控制問題，具有以下特點：

1)建立了一次近似剛?cè)狁詈蟿恿W(xué)模型，充分考慮了動力剛化效應(yīng)，在大角度快速機動背景下更加精確。

2)設(shè)計了利用柔性信息的全狀態(tài)反饋控制器和僅利用角度和角速度信息的動態(tài)輸出反饋控制器，均實現(xiàn)了有限時間姿態(tài)控制，且顯示了其快速穩(wěn)定的優(yōu)越性和高精度的控制性能。

3)另外，在控制器設(shè)計過程中同時考慮了外部干擾和轉(zhuǎn)動慣量不確定性，所以控制器具有良好的魯棒性和工程實用價值。

[1] Ho J Y L. Direct path method for flexible multibody spacecraft dynamics [J]. Journal of Spacecraft & Rockets, 2012, 14(2): 102-110.

[2] Yang J B, Jiang L J, Chen D C. Dynamic modelling and control of a rotating euler-bernoulli beam [J]. Journal of Sound and Vibration, 2004, 274 (3-5): 863-875.

[3] Kane T R, Ryan R R, Banerjee A K. Dynamics of a cantilever beam attached to a moving base [J]. Journal of Guidance, Control, and Dynamics, 1987, 10(2): 139-151.

[4] 蔣建平, 李東旭. 航天器撓性附件剛?cè)狁詈蟿恿W(xué)建模與仿真[J]. 宇航學(xué)報, 2005, 26(3): 270-274. [Jiang Jian-ping, Li Dong-xu. Modeling and simulation for the rigid-flexible coupling dynamics of the spacecraft with flexible appendages [J]. Journal of Astronautics, 2005, 26(3): 270-274.]

[5] Bang H, Ha C K, Jin H K. Flexible spacecraft attitude maneuver by application of sliding mode control [J]. Acta Astronautica, 2005, 57(11): 841-850.

[6] Xiao Y, Ye D, Yang Z, et al. Research on attitude adjustment control for large angle maneuver of rigid-flexible coupling spacecraft [C]. The 8th International Conference on Intelligent Robotics and Applications, Portsmouth, UK, August 24-27, 2015.

[7] Liu H, Zhang Y M, Yang Z H. Mixed H2 /H∞ output feedback attitude control for flexible spacecraft [J]. Journal of Astronautics, 2012, 33(9): 1255-1261.

[8] Hu Q. Robust adaptive sliding mode attitude maneuvering and vibration damping of three-axis-stabilized flexible spacecraft with actuator saturation limits [J]. Nonlinear Dynamics, 2009, 55(4): 301-321.

[9] Zhong C, Yu G, Zhen Y, et al. Vibration suppression and sliding mode attitude control of flexible spacecraft with unknown disturbance and uncertainty [C]. The 33rd Chinese Control Conference, Nanjing, China, July 28-30, 2014.

[10] Zhong C X, Lai A F, Guo Y, et al. On attitude maneuver control of flexible spacecraft without angular velocity sensors [C]. 2013 6th IEEE/SICE International Symposium on System Integration (SII), Kobe, Japan, December 15-17, 2013.

[11] Du H, Li S, Qian C. Finite-time attitude tracking control of spacecraft with application to attitude synchronization [J]. IEEE Transactions on Automatic Control, 2011, 56(11):2711-2717.

[12] Wu S, Wu G, Tan S, et al. Quaternion-based adaptive terminal sliding mode control for spacecraft attitude tracking [C]. 2013 10th IEEE International Conference on Control & Automation, Hangzhou, China, June 12-14, 2013.

[13] Tiwari P M, Janardhanan S, Nabi M U. Rigid spacecraft attitude control using adaptive non-singular fast terminal sliding mode [J]. Journal of Control Automation & Electrical Systems, 2015, 26(2):115-124.

[14] 葉東, 屠園園, 孫兆偉. 面向非沿跡成像的姿態(tài)跟蹤擴展觀測器滑模控制[J]. 宇航學(xué)報, 2016, 37(6):720-728. [Ye Dong, Tu Yuan-yuan, Sun Zhao-wei. Attitude tracking sliding mode control using extended state observer for nonparallel ground track imaging [J]. Journal of Astronautics, 2016, 37(6): 720-728.]

[15] Lu K, Xia Y. Adaptive attitude tracking control for rigid spacecraft with finite time convergence [J]. Automatica, 2013, 49(12):3591-3599.

[16] Liu Z Y, Hong J Z, Liu J Y. Finite element formulation for dynamics of planar flexible multi-beam system [J]. Multibody System Dynamics, 2009, 22(1):1-26.

[17] Deng F, He X, Li L, et al. Dynamics modeling for a rigid-flexible coupling system with nonlinear deformation field [J]. Multibody System Dynamics, 2007, 18(4):559-578.

[18] 楊正賢. 柔性航天器非線性動力學(xué)與控制方法研究[D]. 哈爾濱: 哈爾濱工業(yè)大學(xué)，2011: 48-50. [Yang Zheng-xian. Research on technologies of nonlinear dynamics and control for flexible spacecraft [D]. Harbin: Harbin Institute of Technology, 2011: 48-50.]

[19] Bhat S P, Bernstein D S. Continuous finite-time stabilization of the translational and rotational double integrators [J]. IEEE Transactions on Automatic Control, 1998, 43(5):678-682.

[20] Bhat S, Bernstein D S. Finite-time stability of homogeneous systems[C]. The 1997 American Control Conference, New Mexico, USA, June 6, 1997.

[21] Yang L, Yang J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems [J]. International Journal of Robust & Nonlinear Control, 2011, 21(16):1865-1879.

[22] Yu S, Yu X, Shirinzadeh B, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode [J]. Automatica, 2005, 41(11):1957-1964.

[23] Feng Y, Yu X, Man Z. Non-singular terminal sliding mode control of rigid manipulators [J]. Automatica, 2002, 38(12):2159-2167.

[24] Xu S D, Chen C C, Wu Z L. Study of nonsingular fast terminal sliding-mode fault-tolerant control [J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3906-3913.

[25] Zou A M, Kumar K D, Hou Z G, et al. Finite-time attitude tracking control for spacecraft using terminal sliding mode and chebyshev neural network. [J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society, 2011, 41(4):950-963.

通信地址：哈爾濱市南崗區(qū)一匡街2號3013信箱(150001)

電話：18846455145

E-mail:xiaoy@hit.edu.cn

葉 東(1985-)，男，博士，講師，主要從事航天器姿態(tài)控制及其物理仿真驗證研究。本文通信作者。

通信地址：哈爾濱市南崗區(qū)一匡街2號3013信箱(150001)

電話：(0451)86412357

E-mail:yed@hit.edu.cn

(編輯：牛苗苗)

Finite-Time Output Feedback Attitude Control for Rigid-Flexible Coupling Satellites

XIAO Yan, YE Dong, SUN Zhao-wei

(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

A study on finite-time control is made for the rigid-flexible coupling satellites in a large-angle rapid maneuver. A first-order approximation rigid-flexible coupling dynamic model is set up, considering the serious coupling effect between the deformation of the flexible appendages and the large-scope spatial movement of the central body. Given that all states including the flexible vibration measurements of the satellite system can be measured, a nonsingular fast terminal sliding mode (NFTSM) full state feedback controller is designed in the presence of the model uncertainties and disturbances. The finite-time stability of the system is proved by the Lyapunov theory. Then a modified NFTSM output feedback controller is proposed in the condition that the flexible vibration measurements are not available, and the finite-time output feedback control is based on measurements of the angle and angular velocity only. At last, the numerical simulations of the proposed controllers and comparisons with the controller in present literature together demonstrate the finite-time stability of the control method proposed.

Rigid-flexible coupling satellite; Rapid maneuver; Attitude control; Finite-time control; Terminal sliding mode; Output feedback

2016-10-08;

2017-02-17

國家自然科學(xué)基金(61603115,91438202,61273096)；中國博士后科學(xué)基金(2015M81455)；微小型航天器技術(shù)國防重點學(xué)科實驗室開放基金(HIT.KLOF.MST.201501，HIT.KLOF.MST.201601)；黑龍江省博士后資助經(jīng)費(LBH-Z15085)

V448.22

A

1000-1328(2017)05-0516-10

10.3873/j.issn.1000-1328.2017.05.010

肖 巖(1990-)，男，博士生，主要從事航天器姿態(tài)控制研究。