基于SH模態導波桿的電站高溫結構壁厚測量方法

徐 鴻 郭 鵬 李鴻源 田振華 鄧 博

華北電力大學能源動力與機械工程學院，北京，102206

基于SH模態導波桿的電站高溫結構壁厚測量方法

徐 鴻 郭 鵬 李鴻源 田振華 鄧 博

華北電力大學能源動力與機械工程學院，北京，102206

提出了一種基于SH模態導波桿的電站高溫結構壁厚測量方法，該方法使用導波桿將壓電傳感器與高溫被測結構隔開。通過研究發現非頻散SH模態導波能通過矩形橫截面導波桿將導波信號由傳感器導入到高溫被測結構中。實驗驗證了通過特定夾具以干耦合方式將導波桿固定在被測結構表面可以獲得較好的信號。使用2 MHz中心頻率下的漢寧窗調制正弦波信號實現了對處于不同溫度被測結構壁厚的監測，室溫(25 ℃)時，壁厚測量值與實際厚度相差0.016 mm，高溫被測結構實驗信號也非常好，波速測量值與擬合曲線所得速度值誤差范圍為0.1%～2.5%。

超聲導波; SH0模態; 導波桿; 高溫; 壁厚監測; 數值模擬

0 引言

高溫、輻射環境下的設備在長期的服役過程中，因持續不斷的腐蝕、侵蝕、沖蝕，設備中管道壁面會出現壁厚減薄的現象，最終導致設備和管道失效破壞。材料一旦失效破壞，所引起的非計劃停工會給企業造成巨大的經濟損失，嚴重影響企業的可持續發展，甚至造成人員傷亡。原料狀況、流體流動特性、設備工況的差異性，使得管道的壁厚減薄具有明顯的局部性、突發性、風險性特征，如何實現這些設備和管道的失效預測和預防，一直是企業關注的焦點問題[1-2]。

對于高溫部件局部腐蝕和磨損引起壁厚減薄的檢測，采用常規的超聲無損檢測技術時，壓電傳感器需與被測部件貼合，這在很大程度上限制了壓電傳感器的應用環境。當結構溫度超過300 ℃時，常用壓電傳感器會因為環境溫度超過其居里溫度而使其壓電性能減弱甚至失效，進而使壓電傳感器不能有效地激發和接收超聲波。為激發和接收高溫結構中的導波，文獻[3-4]對耐高溫的壓電材料和傳感器進行了研究。此外，CAWLEY等[5]利用導波桿間接地激發和接收高溫結構中的超聲波。導波桿可當作導波、超聲波的傳輸媒介，將其置于被測結構和壓電傳感器之間，可以有效地將壓電傳感器產生的超聲波傳輸到被測結構中，用于超聲波激發；反之亦然，被測結構中的超聲波可以通過導波桿傳輸到壓電傳感器，用于超聲波的接收。為了減小導波桿中波能量衰減，LYNNWORTH等[6]采用金屬線束作為導波桿，金屬線直徑較小，在頻散曲線上屬于低頻厚積范圍，導波桿中的波近似非頻散傳播；但是金屬線中傳播波信號較弱，要獲得較強的信號就必須將更多的金屬線捆綁在一起。為了測量高溫高壓管道壁厚，李金紅等[7]將與管材相同材料的金屬棒以全焊透的形式垂直焊接在管道外壁面用于壁厚檢測；但該方法易產生焊接缺陷，引起被測結構變形及附加應力，而且該方法采用冷卻裝置對導波桿進行降溫，結構復雜且現場操作十分不便。YOUNGDAHL等[8]將導波桿銅焊在被測部件上，并在導波桿外表面添加翅片結構用于空冷；但翅片結構僅僅使導波桿端部溫度降到100℃，且焊接接頭區域的機械性能會受到影響。

本文研究了矩形截面導波桿中SH模態傳播，并通過干耦合方式將壓電傳感器激發的SH導波有效地導入高溫結構中，實現了高溫及變溫情況下的壁厚檢測。

1 基于SH模態的導波桿

1.1 SH模態的頻散關系

根據質點振動方向的不同，板狀波導介質中的超聲導波主要分為SH波和Lamb波。Lamb波分對稱模態(S)和非對稱模態(A)兩種類型:對稱Lamb波特點是薄板上下表面質點作橢圓運動，中心質點做縱向振動，振動相位相反并對稱于中心;非對稱Lamb波特點是薄板上下表面質點做橢圓運動，中心質點做橫向振動，振動相位相同而不對稱，Lamb波以縱向振動為主。薄板中SH波的質點振動方向平行于板面而垂直于波的傳播方向[1-2]。對于各向同性均勻介質，由Navier運動方程(不考慮體力)可以推導得到SH波的頻散方程：

sin(qh)=0

(1)

cos(qh)=0

(2)

式中，h為平板厚度；cs為橫波波速；ω為角速度；k為波數。

板厚1 mm的不銹鋼板(彈性模量E=216.9 GPa, 泊松比ν=0.2865, 密度ρ=7932 kg/m3)中SH模態的頻散曲線如圖1所示，SH0作為無頻散的波以剪切波速度cs傳播，有cs=3.2 km/s。圖1繪出頻率0～5 MHz的頻散曲線，SH0模態導波屬于非頻散的超聲導波信號，包括垂直于超聲導波傳播方向并平行于導波桿寬度偏振的低階剪切波信號。本文選取的SH0模態導波避免了不需要的較高階模態超聲波的產生，實現了矩形橫截面導波桿中只有單一模態的目的。

(b)群速度圖1 不銹鋼板中SH模態的頻散曲線Fig.1 SH modal dispersion curves for a stainless steel plate

1.2 導波桿中SH模態的傳播

導波波場模擬是導波研究的重要手段，因為模擬不但可以提供詳細的導波信息(波信號、波場、波模態、波結構和頻散關系等)以便于深入研究，而且可以直觀地顯現出導波是如何傳播的[9-10]。利用ANSYS有限元分析軟件對SH0模態超聲導波在導波桿中的波形、能量衰減等特性進行數值分析，可以驗證波源和導波桿設計的正確性和合理性，優化并確定最佳工作參數。

本節中，薄矩形橫截面導波桿的有限元模型采用3D實體單元，即8節點Solid185單元。在導波桿材料參數的定義上，選用304不銹鋼，其彈性模量E= 216.9 GPa,泊松比ν=0.2865,密度ρ=7932 kg/m3。選用導波桿的尺寸：板厚1 mm,板寬15mm,板長100 mm[11]。

彈性波的有限元模擬屬于瞬態動力學分析，為保證計算精度，網格劃分應盡量規整，網格單元尺寸適當。網格尺寸和積分時間步長通常需要滿足以下關系式：

(3)

(4)

式中，Lmax、Lmin分別為單個網格上兩節點間的最大距離和最小距離；λmin為最小波長；nmin為每個波長內的最少網格數(為保證收斂，nmin取值為8～10)；fc為激勵的中心頻率；cmin為彈性波的最小群速度。

由此，本模型采取單元尺寸為0.2 mm的正方形網格進行劃分。

為激發SH0模態，對導波桿端面寬度中心10 mm區域的節點施加水平剪切力載荷，位移載荷方向沿X軸(寬度方向)，計算總時間設為200 μs，時間步長設為0.0625 μs。本小節選用的激勵脈沖導波中心頻率fc為2MHz。圖2為頻率2MHz，不同時間節點t時SH0模態導波在導波桿中傳播的位移等值線云圖。

(a)t=8.0 μs (b)t=20.5 μs

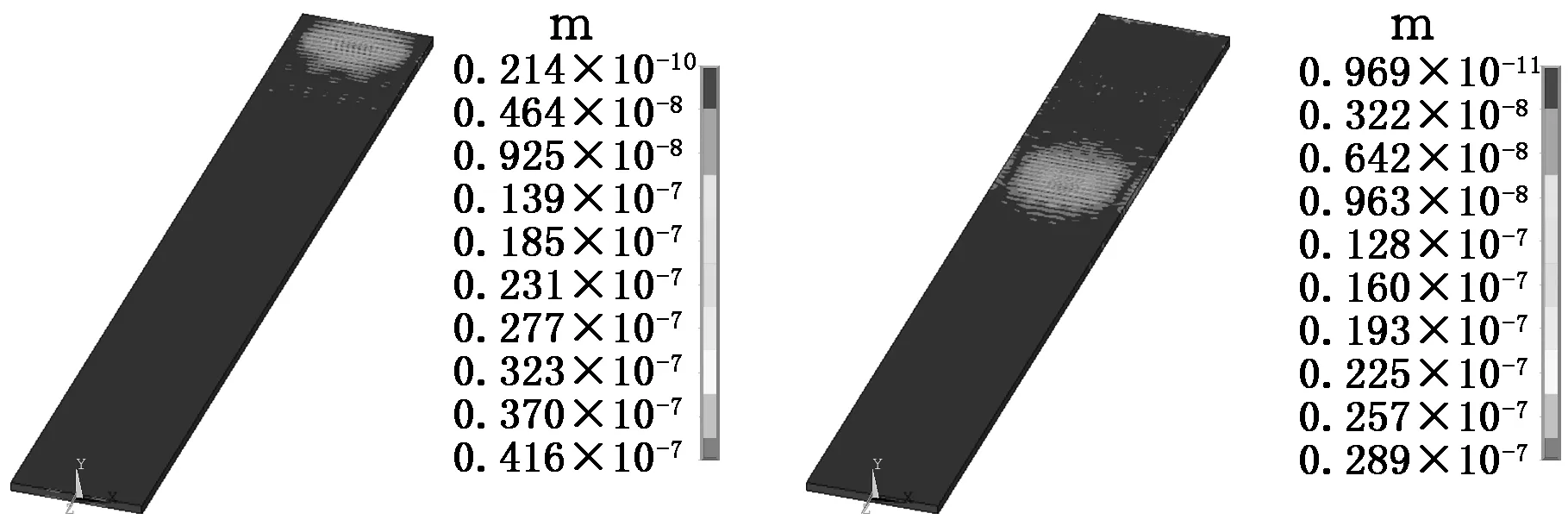
(c)t=33.0 μs (d)t=45.5 μs圖2 2MHz時X方向的位移云圖Fig.2 Simulation results of displacements in X direction at 2MH

由2a、圖2b和圖2c可看出，在傳播過程中SH0模態導波傳播穩定，波包能量集中，無頻散，無明顯的多種模態波，實現了在導波桿中只有單一模態的目的。圖2d為45.5 μs時的位移場，是導波桿底端端面反射波，反射波能量雖有所衰減但仍然集中，傳播穩定性很高。在導波整個傳播過程中，導波桿邊界不存在波能量，說明在導波桿邊界沒有發生波形轉換，能夠獲得較高信噪比的波信號。

如圖3所示，提取導波桿軸線方向(Z方向)距離施加載荷端60 mm處質點位移數據。在中心頻率2 MHz附近質點的位移最大，波包的能量最高、最為集中，無頻散現象，波場未受到導波桿邊界反射波影響，信號的信噪比也較高，說明SH0模態導波傳播穩定，且質點位移隨著傳播距離增加，位移能量有所衰減，但能量依然集中，波場依然穩定。

圖3 2MHz時導波桿軸線方向距激發端60 mm處質點位移曲線 Fig.3 Particle displacement curve of 60 mm in waveguide axis direction at 2MHz

通過以上的SH0模態導波傳播特性的仿真結果分析可知，橫截面尺寸為1 mm×15 mm導波桿在2 MHz的模擬頻率下，SH0模態導波在矩形橫截面導波桿中傳播時波場穩定，無頻散發生，且在界面反射時不發生波形轉換，波形單一，能夠獲得較高信噪比的波信號。

2 導波桿溫度場分析

導波桿作為壓電傳感器和高溫被測部件之間的溫度緩沖波導介質，必須具有良好的散熱性，因此，本節通過ANSYS軟件對其溫度場進行數值模擬，并通過熱電偶測溫實驗來驗證導波桿散熱情況。

矩形橫截面導波桿采用三維模型，選取8節點Solid90單元，304不銹鋼導波桿的相關物理參數為：導熱系數15 W/(m·K)，質量熱容460 J/( kg·K )，密度7932 kg/m3，空氣換熱系數0.025 W/(m·K)。建立導波桿模型，尺寸為：板厚1 mm，板寬15 mm，板長300 mm。使用單元格尺寸0.5 mm×0.5 mm對其進行網格劃分。在導波桿一端的矩形橫截面施加700 ℃的溫度載荷，其余的5個面因考慮其與空氣(25 ℃)的對流換熱施加面載荷，對導波桿進行穩態導熱分析。圖4a示出了導波桿軸線方向(Z方向)的溫度場梯度變化。分別提取導波桿軸線上20 mm、40 mm、60 mm、80 mm、100 mm、200 mm、300 mm處節點的溫度繪制700 ℃模擬溫度分布曲線，如圖4b所示，在導波桿250 mm左右處溫度降至室溫，說明導波桿具有很好的散熱性能。

將K型熱電偶分別布置于導波桿的20 mm、40 mm、60 mm、80 mm、100 mm、200 mm、300 mm、400 mm、480 mm處測量溫度，將導波桿0 mm端插在履帶陶瓷加熱器中，整個加熱器用石英棉包裹嚴實，通過熱處理溫度控制箱設定溫度，從室溫25 ℃到700 ℃，當加熱器穩定在設定溫度時，使用安捷倫測量管理軟件讀取熱電偶測點的溫度，大約250 mm長的不銹鋼導波桿就能將700 ℃降到室溫25 ℃，與導波桿中溫度場模擬結果一致，如圖4b所示，驗證了1 mm×15 mm矩形橫截面導波桿具有很好的散熱性能。

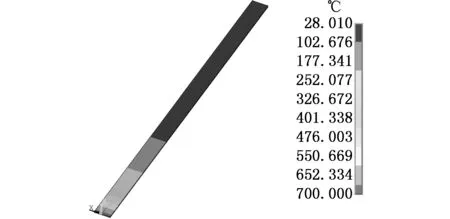
(a)溫度場分布云圖

(b)溫度分布曲線圖4 導波桿(1 mm×15 mm)Fig.4 Rectangular steel strip of 15 mm and 1 mm

3 基于導波桿的高溫結構壁厚檢測

3.1 導波桿與被測部件干耦合方式固定

本節通過特定夾具的夾持力將兩個端面都處理過的導波桿以干耦合方式固定在被測部件上，如圖5所示。實驗中導波桿的尺寸為：長500 mm、寬15 mm、厚1 mm，材質采用304不銹鋼，在夾具夾持的導波桿一端布置可用于測試金屬材料應變的電阻應變片。電阻應變片靈敏系數為2.08，敏感柵尺寸為3 mm×2 mm，基底尺寸為6.5 mm×4.0 mm。通過YSV8320靜態應變測試儀測試導波桿所受的應變ε，同時采集被測鋼板反射回來的導波信號。根據胡克定律σ=Eε(E是彈性模量，E=216.9 GPa)將應變儀獲得的應變ε轉換成應力σ，再依據σ=F/S(S是導波桿與被測鋼板接觸面面積，S=15 mm2)獲得導波桿與被測鋼板之間干耦合所需夾持力F大小，就可以得到干耦合所需夾持力F與導入到被測鋼板中波能量的關系曲線，如圖6所示，波包1是導波桿的端部反射，波包2是被測鋼板后壁一次反射，波包3是被測鋼板后壁二次反射。

圖5 高溫鋼板壁厚測量裝置Fig.5 Steel plate thickness measurement equipment at high temperature

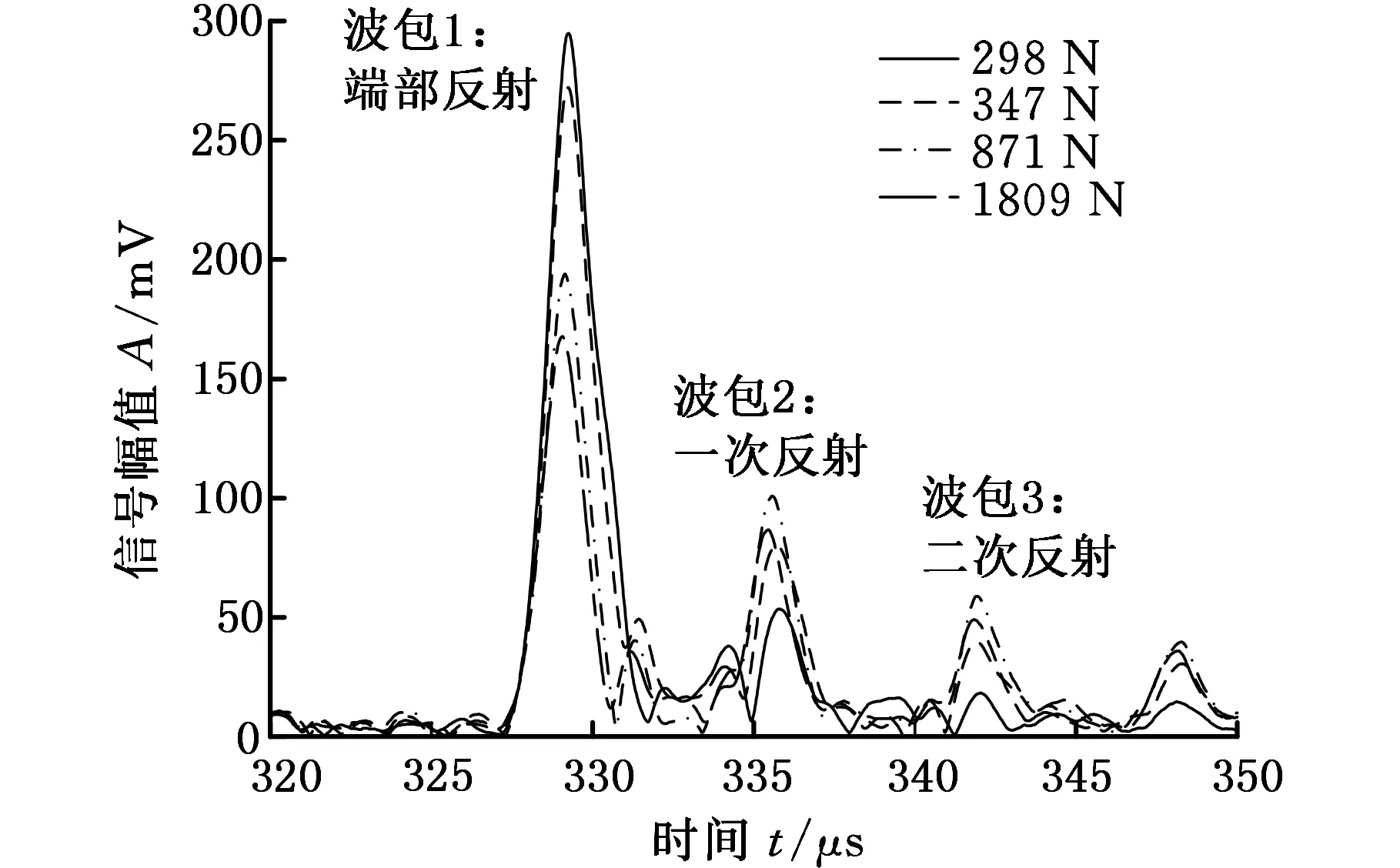
(a)導波信號

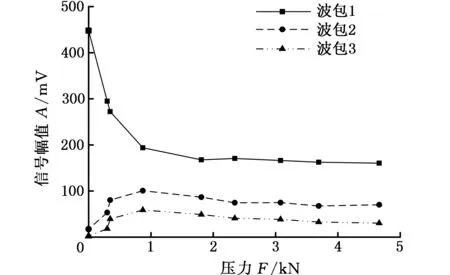
(b)反射波信號幅值曲線圖6 不同夾持力與反射波信號Fig.6 Reflection signal amplitude and different clamping force

由圖6a可知，夾持力由298 N增大到871 N時，通過導波桿導入被測鋼板中的導波信號能量增加，導波桿端面反射波波包1幅值降低，被測鋼板下表面反射波波包2和波包3幅值增大，與圖6b中波包1、2和3的幅值曲線趨勢一致，在1 kN附近波包幅值都達到極值，之后幅值降低并趨于穩定。導波桿所受的夾持力過大(1809 N)時，導波桿會發生彎曲，造成導波桿端面與被測鋼板之間力變小，接觸面積也會減小，使導波桿導入到被測鋼板中的波能量減少，被測鋼板中反射波能量未能很好地導入到導波桿中，導致干耦合效果變差。綜上，導波桿中的波能量在1000 N附近時能被很好地導入到被測鋼板中，且被測鋼板中反射波能量能很好地通過連接處被探頭接收。

3.2 高溫鋼板壁厚測量實驗

超聲導波的測厚是通過聲波的脈沖回波方法實現的。圖7展示了SH0波在導波桿和被測鋼板中的傳播路徑，在后面的實驗中，我們只關注前三個反射波，因為前三次反射波的能量較高、幅值大、信噪比較高。在導波桿端部的直入射橫波探頭接收到的第一個反射波是導波桿端面的反射波，第二個反射波是被測鋼板后壁的一次反射波，第三個反射波是被測鋼板后壁的二次反射波。

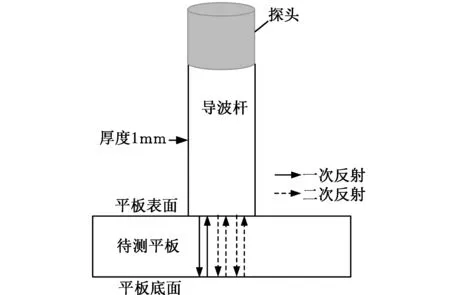
圖7 超聲導波測厚原理示意圖Fig.7 Schematic diagram of thickness measurement by ultrasonic guided wave

在被測鋼板壁厚測量實驗中導波桿的尺寸為：長500 mm、寬15 mm、厚1 mm。被測鋼板的尺寸為：長150 mm、寬80 mm、厚10 mm。導波桿、被測鋼板和夾具的材料都采用304不銹鋼，探頭采用直徑12.5 mm直入射橫波探頭(Olympus V154)，將其通過蜂蜜耦合到矩形導波桿的端面，探頭的極化方向與導波桿的寬度方向平行，能夠在導波桿中激發出SH0波。導波桿與被測部件采用特定夾具實現干耦合。整個實驗裝置如圖5所示。

本文采取單激單收模式，在實驗裝置處于室溫(25 ℃)環境中，任意函數發生器(Tektronix AFG 3022)產生頻率為2 MHz時，激發5周期漢寧窗調制正弦波信號給直入射橫波探頭，再經過導波桿，導入到被測平板上，被測平板產生的反射波會沿原路返回被探頭接收，獲得的反射波信號如圖8所示，該套設備能接收到平板底面1次和2次反射，信噪比較好，波包易于分辨。已知平板厚10 mm，反射信號時間差6.26 μs，計算得到波速3.19 mm/μs，接近SH0模態波速3.2 mm/μs(2 MHz時)，誤差為0.3%，壁厚測量值為10.016 mm，與實際平板厚度相差0.016 mm，說明此裝置在室溫下能較好地測量平板壁厚。

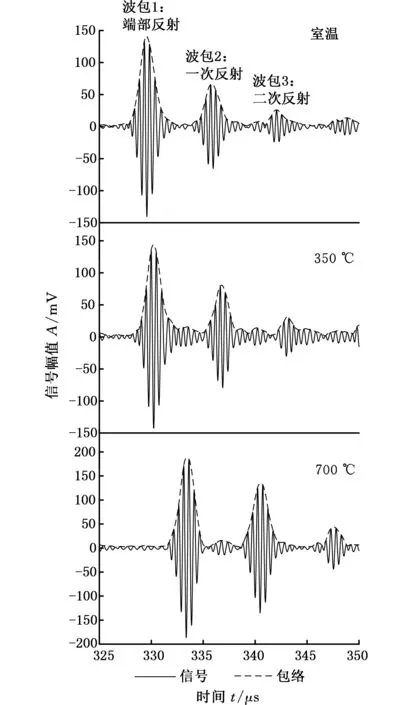
圖8 不同溫度時反射波信號Fig.8 Reflected wave signal under different temperature

將固定好的壁厚測量裝置放置在履帶陶瓷加熱器上，并進行嚴密包裹，在被測鋼板上下表面和導波桿上不同位置100 mm、200 mm、300 mm、400 mm、480 mm處布置高溫熱電偶，如圖5所示，通過熱處理溫度控制箱控制加熱毯的溫度，從室溫25 ℃逐漸升溫到700 ℃，350 ℃和700 ℃時反射波信號如圖8所示。由圖8可知,隨著溫度升高，反射信號的信噪比變好，波包信號更明顯。同時可以明顯看出反射波波包的延遲，為了直觀地觀察幅值和能量的變化情況，我們通過溫度-時間曲線來分析，如圖9所示。隨著溫度升高，三個波包傳播時間延長，與圖8的反射波波包延遲相一致。隨著溫度升高，波包2和波包3幅值有增大的趨勢，說明通過干耦合方式能將信號能量導入到平板中。

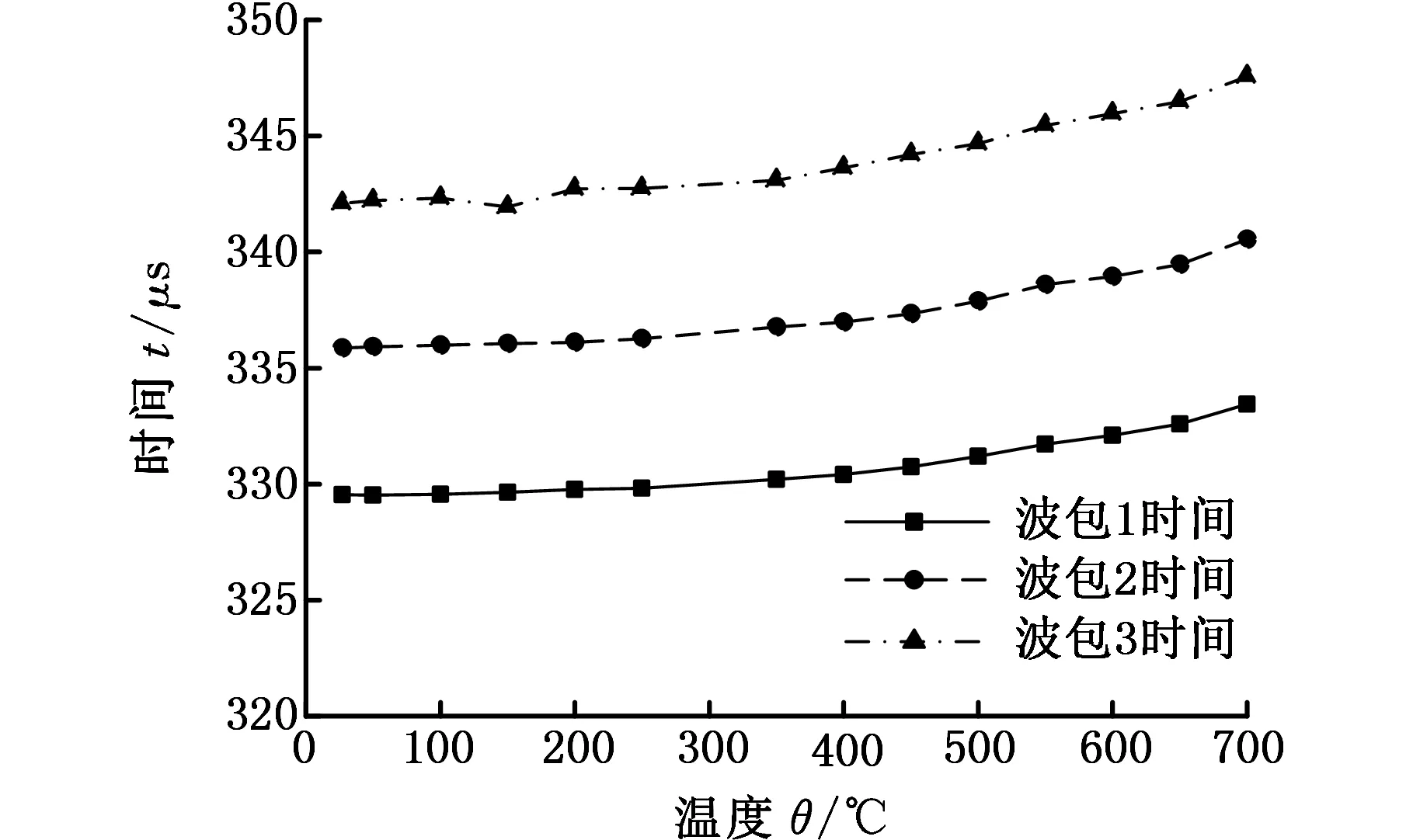
(a)溫度-時間

(b)溫度-波速圖9 高溫壁厚測量實驗數據曲線Fig.9 Experimental data curve of wall thickness measurement at high temperature

被測鋼板厚10 mm，遠遠小于導波桿長度(500 mm)，可以不考慮平板中溫度分布不均勻性所產生的影響。如圖9a所示，隨著被測鋼板溫度的升高，對傳感器接收到的反射波信號進行分析，發現反映壁厚信息的三個波包均發生時間延遲，反射信號時間差也由常溫時的6.26 μs增大至700 ℃時的7.06 μs。不同溫度時，不銹鋼的熱膨脹系數不同，導波傳播速度也相應發生變化，造成反射波波包發生延遲現象，如圖9b所示。速度測量值與擬合曲線所得速度值誤差范圍為0.1%～2.5%，波速相差0.08～0.003 mm/μs。擬合的校正決定系數可以反映擬合結果的好壞，越接近1，擬合結果越好。本文中高溫實驗的校正決定系數為0.93，說明高溫實驗擬合結果很好。導波傳播速度由常溫時3.2 mm/μs減小至700 ℃時2.86 mm/μs，但是被測鋼板由室溫升至700 ℃的過程中，被測鋼板壁厚測量值范圍為9.63～10.1 mm，誤差范圍為0.16%～3.7%。上述結果驗證了即使在高溫環境中，利用導波桿和直入射橫波探頭可以對被測鋼板壁厚進行測量或監測。

4 結論及展望

本文研究表明2MHz中心頻率下的SH0模態導波在尺寸1 mm×15 mm×500 mm矩形橫截面導波桿中傳播的波形穩定，無頻散發生，且在界面反射時無波形轉換，導波傳輸信噪比高；通過特定夾具以干耦合方式將導波桿固定在被測結構表面可以實現對高溫被測部件實時定點測厚，在25～700 ℃溫度變化范圍內，鋼板壁厚的測量誤差較小，在0.16%～3.7%之間。未來，在此測厚技術的基礎上添加無線網絡設備，實現壁厚測量數據無線傳輸到中控室，通過數據管理系統對數據分析處理，彌補現有監測技術的缺點和不足，具有一定的創新性和應用價值。

[1] 田振華, 徐鴻, 李鴻源, 等. 基于單激發端多接收端壓電陣列的板內損傷檢測[J]. 中國機械工程,2014,25(22): 3077-3080,3087. TIAN Zhenhua, XU Hong, LI Hongyuan, et al. Damage Detection for a Plate Based on a Single-transmitter Multi-receiver PZT Array[J]. China of Mechanical Engineering, 2014,25(22):3077-3080，3087.

[2] 田振華, 徐鴻, 楊志磊. 基于扭轉模態的管道裂紋聚焦成像[J]. 中國機械工程, 2013,24(1):85-89. TIAN Zhenhua, XU Hong, YANG Zhilei. Focusing Imaging of Cracks in Pipes Based on Torsional Modes[J]. China of Mechanical Engineering,2013,24(1):85-89.

[3] MCNAB A, KIRK K J, COCHRAN A. Ultrasonic Transducers for High Temperature Applications [J]. Science Measurement and Technology, IEE Proceedings,1998,145:229-236.

[4] TITTMANN B, AASLAN M. Ultrasonic Sensors for High Temperature Applications [J]. Japanese Journal of Applied Physics,1999,38(5):3011-3013.

[5] CAWLEY P, CEGLA F B. Ultrasonic Non-destructive Testing: U.S. Patent 8381592[P].2013-02-26.

[6] LYNNWORTH L C, LIU Y, UMINA J A. Extensional Bundle Waveguide Techniques for Measuring Flow of Hot Fluids[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control,2005,52(4):538-544.

[7] 李金紅,張雅超，邸艷玲，等.采用導波桿方式超聲檢測高溫高壓管道壁厚的方法[J].NDT無損檢測，2009,31(8)：593-595,599. LI Jinhong, ZHANG Yachao, DI Yanling, et al. Ultrasonic Thickness Measurement Method for High Pressure and Temperature Tube by Waveg-uide Bar[J]. Nondestructive Testing, 2009, 31(8):593-595,599.

[8] YOUNGDAHL C A, ELLINGSON W A. Nondestructive Monitoring of Erosive Wear at Synfuels Pilot Plants[J]. Mater. Performance(United States),1985,24(1):48-53.

[9] ROSE J L. Ultrasonic Waves in Solid Media[M]. Cambridge: Cambridge University Press,1999.

[10] GIURGIUTIU V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors[M]. Boston, MA: Academic Press, 2008.

[11] CEGLA F. Energy Concentration at the Center of Large Aspect Ratio Rectangular Waveguides at High Frequencies[J]. The Journal of the Acoustical Society of America, 2008,123(6):4218-4226.

(編輯 袁興玲)

Thickness Measuring Method of High-temperature Power Plant Structures Based on SH Mode Waveguide

XU Hong GUO Peng LI Hongyuan TIAN Zhenhua DENG Bo

School of Energy, Power and Mechanical Engineering, North China Electric Power University, Beijing,102206

It is significant to put forward a thickness measuring method of high temperature power plant structures based on SH mode, which used a waveguide to isolate the transducers from the high-temperature measurement zones. It was found that a nondispersive SH mode guided wave in rectangular waveguide was employed to transmit the guided wave signals from the transducers to the measurement zones. In addition, experiments were investigated by dry-coupled to attach the waveguides to the components, which shows that clamping the waveguides to the component surfaces may get best results. By using Hanning window modulated sine wave signals with 2 MHz center frequency, the thickness difference of the measured values and actual values of wall thickness is 0.016 mm at the room temperature(25 ℃). Performance at high temperatures was tested without signal degradation. The error ranges of wave velocity measurement values and the velocities of the fitting curve are 0.1% to 2.5%.

ultrasonic guided wave; SH0 mode; waveguide; high temperature; thickness monitoring; numerical simulation

2016-11-02

國家自然科學基金資助項目(51134016)；中央高校基本科研業務費專項資金資助項目(2016XS25)

TB559;O347.4

10.3969/j.issn.1004-132X.2017.07.001

徐 鴻，男，1959年生。華北電力大學能源動力與機械工程學院教授、博士研究生導師。研究方向為電站設備狀態監測、控制與運行，結構健康監測，超聲無損檢測新技術。發表論文70余篇。E-mail：xuhong@ncepu.edu.cn。郭 鵬，男，1986年生。華北電力大學能源動力與機械工程學院博士研究生。李鴻源，男，1985年生。華北電力大學能源動力與機械工程學院博士研究生。田振華，男，1987年生。華北電力大學能源動力與機械工程學院博士研究生。鄧 博，男，1981年生。華北電力大學能源動力與機械工程學院博士研究生。