混頻器和濾波器非線性效應對MWC系統的影響
李萬泉,黃知濤,馮道旺,王 翔
(國防科學技術大學電子科學與工程學院, 湖南 長沙 410073)
混頻器和濾波器非線性效應對MWC系統的影響
李萬泉,黃知濤,馮道旺,王 翔
(國防科學技術大學電子科學與工程學院, 湖南 長沙 410073)
近年來提出的調制寬帶轉換器欠奈奎斯特采樣系統,可以在遠低于奈奎斯特頻率下無失真采樣寬帶稀疏多頻帶信號。但是實際系統中混頻器和低通濾波器非線性效應的影響會導致重構的信號存在失真。利用Rapp模型在理論上分析了器件的非線性效應造成信號重構誤差的原因,并通過仿真實驗,分析了非線性效應對支撐集重構概率的影響以及通道數和輸入信噪比在降低系統誤差上的作用。仿真結果表明,器件的非線性效應會降低系統的重構性能;提高通道數和輸入信噪比可以提高支撐集重構概率,改善系統的性能。
調制寬帶轉換器;欠奈奎斯特采樣;非線性效應;支撐集
0 引言
傳統的采樣要遵循奈奎斯特采樣定理,即采樣速率必須達到模擬信號帶寬的兩倍才能無失真地恢復原始模擬信號。由于接收信號頻譜范圍很寬,目前商用的ADC器件往往難以滿足Nyquist采樣頻率的要求。即使可以達到采樣率要求,其巨大的數據量也會給后續存儲、傳輸和處理造成較大壓力。2005年,壓縮感知理論[1-2]的提出為解決這一問題提供了新的思路與方法。2009年,以色列學者Mishali和Eldar提出了一種多通道結構的寬頻帶稀疏信號壓縮采樣結構——調制寬帶轉換器(MWC)[3-4],主要由混頻器、低通濾波器和低速ADC組成。調制寬帶轉換器理論上可通過現有的器件實現,降低了采樣率,并可以在不需要任何先驗信息的條件下全盲恢復原始信號[5-6]。基于MWC的欠奈奎斯特采樣技術在衛星導航、雷達探測、電子對抗等領域有著廣泛的應用前景。混頻器和低通濾波器是MWC系統中的關鍵器件,混頻器將系統前端接收到的信號與周期偽隨機序列混頻,讓信號的頻譜擴展到整個通頻帶;通過低通濾波器對混頻后的信號濾波,使得在基帶也包含有輸入信號的完整信息。然而,實際硬件系統中器件非線性效應的影響,導致MWC系統無法正確完成對輸入信號的重構。本文重點針對混頻器和低通濾波器的非線性效應對MWC系統的重構性能影響,展開理論和仿真分析,研究支撐集正確重構概率隨非線性度的變化關系。
1 MWC采樣理論
1.1 MWC采樣原理
MWC壓縮采樣系統通過多通道隨機序列混頻的方式將寬帶稀疏模擬信號的所有頻率成分調制到低頻段來實現低采樣率[3]。其系統原理框圖如圖1所示。
輸入信號同時進入m個通道,在第i個通道被周期為Tp(頻率為fp)的偽隨機序列pi(t)混頻,混頻后再經過截止頻率為1/2Ts的理想低通濾波器進行濾波,最后以1/Ts的速率進行低速采樣,得到各個頻帶內的m組采樣值,用于信號的重建。
偽隨機序列pi(t)由于具有周期性 ,每個周期內以伯努利分布隨機取值M個±。時域模型可以表示為:
pi(t)=αik,kTp/M≤t≤(k+1)Tp/M,0≤k≤M-1
(1)
式中,αit為{+1,-1}。可以得到周期函數pi(t)的傅里葉變換pi(f)為:
(2)
式中,Cil表示偽隨機信號的傅里葉系數:
(3)
信號與偽隨機信號相乘再通過理想低通濾波器H(f),然后以fs為采樣率進行低速采樣得到輸出yi(n),其DTFT可以表示為:
(4)
式中,L0=[fNYQ+fs/2fp?-1,fNYQ是信號x(t)的Nyquist采樣率。
將(4)式寫成矩陣的形式,得到MWC采樣系統在頻域上壓縮感知模型:
(5)
式中,Y(f)是大小為m×1的矩陣,第i個分量表示為yi(f)=Yi(e-j2πfTs)。m×L的矩陣A的元素系數為cil。Z(f)是大小為L×1的矩陣,表示為Z(f)=[z1(f),…,zL(f)]T。且zi(f)=X(f+(i-L0-1)fp),1≤i≤L,f∈[-fs,+fs],其中L=2L0+1。
對(5)式取逆離散時間傅里葉變換,可以得到MWC在時域上的壓縮感知模型:
y(n)m×d=Am×Lz(n)L×d
(6)
式中,下標d是采樣數據長度。
傳統雙邊匹配決策方法建立在期望效用理論基礎之上,假設匹配主體是完全理性的,然而在實際匹配過程中,匹配主體在行為上并非完全理性,而表現為參照依賴和損失規避等心理行為特征。1979年Kahneman和Tversky通過大量的實驗研究發現了決策者的實際決策行為與期望效用理論相背離的現象,并引入心理學的研究成果,提出了前景理論[22-23]。前景理論使用價值函數取代期望效用理論中的效用函數,能很好地描述和表達匹配主體在決策過程中的參照依賴和損失規避等心理行為特征。
給定A和Y(n),通過求解式(6),可以得到未知信號z(n),從而可以求得原信號。由于m 1.2 MWC采樣系統重構 從m個通道的低速采樣序列yn(n)中恢復信號x(t),主要包括兩個步驟:一是確定頻譜的支撐集;二是根據觀測方程,從采樣點中重構出信號。 對于未知的支撐集S=suppZ(Fp),可用連續到有限模塊(CTF)[3]求解,其結構如圖2所示。 CTF首先計算: (7) (8) 得到S后,取出A中所對應S所在的列構成新的矩陣As,從而可以計算各個子帶信號: (9) (10) 式中,h(t)=sinc(πt/Ts)。經過調制得到重構模擬信號: (11) 式中,Re(·)和Im(·)分別表示其實部和虛部。 2.1 問題描述 實際應用中,混頻器和低通濾波器的非線性效應是MWC硬件系統中一個很關鍵的非理想因素。當輸入信號大到一定程度時,混頻器和低通濾波器會進入非線性工作狀態,表現出非線性特性,輸出信號達到飽和,不再隨輸入信號線性變化。器件的非線性效應可用Rapp模型[8]描述,具體可用下式表示。 (12) 式中,Vfull scale為器件的飽和輸入電壓,r為平滑因子,決定著混頻器和低通濾波器由線性區過渡到飽和區的平滑程度。在進入飽和區前,r越大,輸出與輸入關系越接近線性,器件的線性度越好。可以改變r的值,得到混頻器和低通濾波器的不同非線性特性。Rapp模型非線性特性曲線如圖3所示。 2.2 影響分析 (13) (14) 式中,αmixer為混頻器的非線性因子,由于Vfull scale為輸入信號的滿幅度,因此x(t)/Vfull scale的最大值為1。在式(14)中,當pi(t)的傅里葉級數系數Cil所占權重相對較小,且平滑因子r相對較大時,非線性變化相對很小,混頻器基本工作在線性區域,信號幾乎不會發生非線性失真。 與混頻器類似,當處理的信號大到一定值時,低通濾波器會進入非線性工作狀態,使輸出信號發生非線性失真,導致支撐集正確重構概率降低。低通濾波器的非線性效應同樣可以用Rapp模型來描述,具體用公式表示為: *x(t)pi(t) (15) (16) 式中,αlpf為低通濾波器的非線性因子,h(t)與x(t)·pi(t)的卷積結果即為低通濾波器的輸出。由于低通濾波器的傳輸增益為1,并且它把帶外的能量全部濾除,信號幅度也比混頻器輸入信號的幅度要小,所以有: h(t)*x(t)pi(t)≤x(t)pi(t) (17) 從而,αlpf≤αmixer。當混頻器的非線性因子αmixer≈1時,低通濾波器也基本工作在線性區域,信號不會發生非線性失真,系統的重構性能不會受到影響。 本節通過仿真進一步分析混頻器和低通濾波器非線性效應對MWC系統的影響程度。選用一個頻帶數目的N=6多頻帶信號進行研究,多頻帶信號為: (18) 式中,sinc(x)=sin(πx)/(πx)。實驗設置B=50MHz,信號各頻帶能量系數為Ei=[1,2,3],時間偏移τi分別為0.788μs、1.379μs、0.394μs,信號Nyquist采樣率fNYQ=10GHz,每個頻帶的載頻在[-fNYQ/2,fNYQ/2]內隨機選取。采樣時MWC參數設置如下:fs=fp=51.28 MHz;L0=97,L=2L0+1=195。在輸入信噪比為10dB和25dB條件下,對不同的通道數分別進行仿真。仿真時,改變混頻器和低通濾波器的平滑因子r,在器件的不同非線性度的情況下,各進行100次實驗,計算出系統能夠正確重構支撐集的概率。 輸入信噪比為10dB和25dB時,支撐集正確重構概率隨混頻器非線性度的變化曲線如圖4和圖5所示。可以看出,在高輸入信噪比的條件下,系統能免受一定程度非線性效應影響,比低輸入信噪比的系統表現出更優越的重構性能。當系統的通道數大于或等于30時,混頻器的非線性效應不會大幅度地降低支撐集的正確重構概率。通道數越多,式(14)中pi(t)的傅里葉級數系數cil所占權重越小,單路通道混頻器非線性效應會降低,則非線性因子αmixer≈1,混頻器工作在線性區域,信號不會發生非線性失真,支撐集的重構概率也會隨之提高,這與實驗前的分析是一致的。 輸入信噪比分別為10dB和25dB,支撐集正確重構概率隨低通濾波器非線性度的變化曲線如圖6和圖7所示。和混頻器的非線性效應類似,當系統的通道數大于等于30時,低通濾波器的非線性效應不會大幅度地降低系統的重構性能,特別是輸入信噪比為25dB,重構概率幾乎不會下降,高輸入信噪比的系統表現出更佳的重構性能。在低通濾波器非線性最嚴重情況下,即平滑因子r= 1,系統的通道數為20,輸入信噪比為10dB和25dB時,重構概率分別為23%、59%;若非線性器件是混頻器,重構概率分別為15%和67%。可見,在相同條件下,混頻器和低通濾波器的非線性效應對系統的影響相差不大。提高通道數和輸入信噪比可以很明顯地提高支撐集正確重構概率,系統的重構性能也得到大幅度的改善。 本文介紹了MWC采樣系統的工作原理,利用Rapp模型在理論上分析了混頻器和低通濾波器非線性效應對MWC系統的影響,并對其進行了仿真驗證。仿真結果表明,器件的非線性效應會降低支撐集重構概率,影響系統的重構性能;提高通道數和輸入信噪比可以提高支撐集正確重構概率,降低混頻器和低通濾波器非線性效應對系統的影響,改善系統的性能。對于設計實現MWC系統具有一定的指導意義。■ [1] Donoho D. Compressive sensing[J]. IEEE Trans. Information Theory, 2006, 52(4): 1289-1306. [2] Baraniuk R.Compressive sensing [J]. IEEE Signal Processing, 2007, 24(4): 118-120. [3] Mishali M, Eldar YC. From theory to practice: Sub-Nyquist sampling of sparse wideband analog signals[J]. IEEE J. Select. Top. Signal Processing, 2010, 4(2): 375-391. [4] Mishali M, Eldar YC, Tropp JA. Efficient sampling of sparse wideband analog signals [C]∥2008 IEEE 25th Convention of Electrical and Electronics Engineers in Israel,2008: 290-294. [5] Mishali M, Eldar YC. Xampling: analog to digital at sub-Nyquist rates[J]. Circuits Devices & Systems, IET, 2011, 5(1): 8-20. [6] Mishali M, Eldar YC. Wideband spectrum sensing at sub-Nyquist rates[J]. Signal Processing Magazine, 2011, 28(4): 102-135. [7] Tropp JA, Gilbert AC. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Trans. on Information Theory, 2007, 53(12): 4655-4666. [8] Rapp C. Effects of the HPA-Nonlinearity on a 4-DPSK/OFDM signal for a digital sound broadcasting system[C]∥2nd ECSC Conf., 1991 :179-184. Analysis of the influence of non-lineartiy effects of mixer and filter on MWC system Li Wanquan, Huang Zhitao, Feng Daowang, Wang Xiang (College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, Hunan,China) In recent years, the sub-nyquist sampling system of modulated wideband converter (MWC) is proposed, and it could take sample of wideband sparse multiband signal without distoration far below the nyquist frequency. But in the actual system, the non-linearity effect of mixer and low pass filter can lead to the distortion of the reconstructed signal. The reason of signal reconstruction error caused by the non-linearity effects of the devices is analyzed theoretically by Rapp model. And through simulation experiment, the influence of the non-linearity effects on reconstruction probabilities of the support set and the effect of channel number and input SNR in reducing the system error are analyzed. The simulation results show that the non-linearity effects of the devices could decrease the reconstruction abilities of the system and it can increase reconstruction probabilities of the support set and improve the performance of the system by increasing the number of channels and input SNR. modulated wideband converter; sub-nyquist sampling; non-linearity effects; support set 2017-01-05;2017-02-26修回。 李萬泉(1992-),男,碩士研究生,主要研究方向為信號處理與壓縮采樣。 TN975 A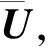
2 非線性效應分析
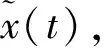
3 仿真實驗結果與分析
4 結束語

