基于議價模型的航空聯盟動態轉讓價格研究

顧穎菁，朱金福

（南京航空航天大學民航學院，江蘇 南京 211106）

基于議價模型的航空聯盟動態轉讓價格研究

顧穎菁，朱金福

（南京航空航天大學民航學院，江蘇 南京 211106）

隨著全球經濟一體化的發展，航空聯盟的不斷加深，航空聯盟成員如何合理地分配收益已經成為航空公司研究的重要問題。用討價還價動態博弈法研究了航空聯盟中市場航空公司與承運航空公司在完全信息與非完全信息下的轉讓價格問題，并建立了非完全信息下按比例分配多階段議價模型。研究結果表明：討價還價博弈下的轉移價格能夠激勵航空公司的銷售，市場航空公司在不完全信息情況下，會獲得較高收益；承運航空公司在非完全信息下，會獲得較高收益。非完全信息下按比例分配多階段議價模型彌補了現有分配方式不足，既保證有利于航空聯盟的票不被拒絕，也確保航空公司的利益不會減少。

航空聯盟；轉移價格；動態博弈；議價模型

航空公司即使在加入航空聯盟后，他們的最終目的還是自身利益最大化，Boyd[1]和Wright等[2]提出航空聯盟會在航線運營前制定收益分配協議（SPAs），該協議規定了收益分配是以怎樣的方式進行收益分配，主要有以下兩種方式：

1）按比例分配支付：根據航空聯盟協議，市場航空公司收到一個旅客請求，票價為，根據比例分配確保自己航段可售，將剩余票價給承運航空公司，承運航空公司確認可行，出售，確認不可行，拒絕。這種分配方式是目前航空聯盟里使用最多的方式，但可能會導致增加航空聯盟收益的票被拒絕，例如：航空公司1承運A—B航段，票價苊525，航空公司2承運B—C航段，票價苊1530，對于A—C段的票，分配比例為20%和80%。當航空公司1接收到一個旅客請求，價值苊2 250，對于整個聯盟，苊2 250>苊525+苊1 530，應出售，對于航空公司1，苊2 250×20%=苊450<苊525，所以拒絕。

2）支付轉讓價格：根據合作協議，市場航空公司在使用承運航空公司艙位時，支付給承運航空公司轉讓價格。Vinod[3]提出了影子價格為動態的轉讓價格，影子價格以承運航空公司的期望收益，但該分配方式對承運航空公司不利；Graf等[4]提出的基于期權方式，即市場航空公司通過預先支付期權價格給承運航空公司，保留一定數量的艙位，若使用則支付剩余價格，如不使用，期權價格將不退還；Cetiner等[5]提出用合作博弈論的方法研究航空聯盟的收益共享機制，通過計算“核”來評價現有分配機制的公平性，并且分析了相較于集中控制，非集中情況下收益分配是否受到了影響以及影響了多少，研究得出，基于航段自身價值的分配方式優于其它方式。

在航空聯盟收益管理中，收益分配與艙位控制相輔相成，De la Torr[6]討論了代碼共享下的艙位分配方法，一種是由運營商控制固定或非固定艙位數，這種區域空間代碼共享并沒有得到廣泛使用，另一種是自由銷售協議，也是目前最常用的，他還提出了由于高估代碼共享航線可能造成潛在損失，可以通過按比例分配收益來避免個體損失；Topaloglu[7]針對多航段聯盟網絡的艙位控制問題，在多航段聯盟網絡中，假設航空公司獨立地進行艙位容量控制的決策，只有出售機票的航空公司才能決定接受或拒絕旅客到達請求，建立了單一航空公司的艙位控制線性規劃模型，通過對偶方法得到航空公司的收益分配份額；Waldemar等[8]用納什均衡方法研究了平行聯盟和互補聯盟內的競爭模型，第一次在模型中考慮了多等級艙位。

目前確定轉讓價格多少在于航空聯盟協議或者市場航空公司報價，承運航空公司只能被動的接受或者拒絕，沒有再次議價的機會。本文使用了討價還價博弈方法，討價還價模型是一個完全信息動態博弈模型，通過共同收益，機會收益，以及對差值可接受的委曲程度共同作用于決策過程，是雙方共同作用的結果，通過討價還價博弈方法確定支付價格，可以最大程度上保證收益分配的公平性。在研究中，還涉及到EMSR方法，Peter[9]在他的博士論文中發展了Littlewood[10]的方法并給出嚴格的證明，該方法引起了許多后續研究，也在很多領域都得到應用。張秀敏等[11]使用投標價格法，在鐵路客運領域提出改進方法：隱藏價格（EMSR）法，對各區段座位實行嵌套結構管理。

蔣菱等[12]建立不完全信息條件下的討價還價模型，用逆襲歸納法解出了模型的理論均衡解，并得到了實驗均衡解，結果表明實驗均衡解達不到理論均衡解，并得出在不完全信息下，報價順序的先后決定了參與方分配利益的多少；詹文杰等[13]研究了有限理性假設下“多對多”討價還價的策略，建立“雙種群”復制動態模型，證明了只有嚴格納什均衡才能成為“多對多”討價還價的演化穩定策略；杜少甫等[14]用Nash討價還價博弈方法建立了供應鏈效用的公平關切框架，構建了描述性的行為運籌模型，探討零售商的公平關切程度如何影響供應鏈成員的決策；簡惠云等[15]分析與比較風險規避型供應鏈分別采取Stackelberg博弈和Nash討價還價博弈時的最優化決策，探討供應鏈主導方如何根據合作伙伴的風險規避水平選擇契約和博弈機制。

1 完全信息下的討價還價模型

互補型航空聯盟，即在一條航線上，成員航空公司分別承運不同的航段。市場航空公司是指在一條共同承運航線上出售機票的航空公司，承運航空公司是指未出售機票，但參與了承運的航空公司。成員航空公司共同運營的航線上都可以出售機票，市場航空公司和承運航空公司并不特指某一方，而是根據出售機票方，相互轉換。轉讓價格是指市場航空公司為使用承運航空公司艙位所支付給承運航空公司的價格，也是收益分配的一種方式。

1.1 條件假設與參數說明

1）完全信息是指市場航空公司和承運航空公司能夠了解各自的艙位等級、需求以及當前實際的銷售情況。

2）當市場航空公司收到一個票價為p聯運旅客的請求時，市場航空公司和承運航空公司單個航段上當前最低期望收益和最高期望收益為［a1，a2］，［b1，b2］，當前最低期望收益為此時的邊際收益，可用EMSR方法計算，當前最高期望收益為此航段上的最高票價。市場航空公司接受使用承運航空公司艙位的價格區間為［p-a2，p-a1］，承運航空公司同意承運的價格區間為［b1，b2］（其中p-a1為市場航空公司使用承運航空公司艙位的最高支付價格，b1為承運航空公司同意承運的最低接受價格，并且p-a1≥b1）。

3）令r為談判成功的最優解，則r∈［b1，p-a1］，其中p-a1－r為市場航空的剩余，r－b1為承運航空的剩余。

4）討價還價是動態博弈過程，分為若干階段，由市場航空公司先出價，承運航空公司同意即停止，若不同意，則由承運航空公司出價。

5）談判過程具有時間價值，隨著談判時間的加長，失去該旅客的幾率加大，雙方的收益都將有損耗。雖然失去旅客是共同行為，但是雙方對于失去該旅客的害怕程度不一樣，將害怕程度轉設為“客座率”，分別為σ1，σ2（0≤σ1≤1，0≤σ2≤1），σ1，σ2越大，表明“客座率”越高，害怕失去該旅客的程度越低。

1.2 模型建立

在完全信息狀態下，將談判區間［b1，p-a1］投影到［0，1］上，區間［0，1］中的r′為r在相應區間上的映射：r′＝（r－b1）／（p-a1－b1），可以轉化為經典魯賓斯坦的分蛋糕博弈。他的分析思路，是根據最后被接受的報價提出者的不同，為該參與人提出最“合理”的報價，這一報價是根據兩人議價能力（即貼現因子）而得出的一次性最優報價值。

當議價階段不受限制時，得到Nash均衡的結果是

由式（1）可知，由于市場航空公司接受旅客請求，具有先出價權，并且獲得的收益大于承運航空公司，該方式可以激勵成員航空公司售票；式（2）為具體轉讓價格。

1.3 完全信息下的艙位轉讓流程

航空公司1與航空公司2實行聯盟內合作，當航空公司1接收到一個票價為p的旅客請求，此時航空公司1為市場航空公司，如果票價小于兩家航空公司的最低期望收益之和，市場航空公司直接拒絕該旅客，如果票價大于或等于兩家航空公司的最低期望收益之和，市場公司同意接受該旅客，并與航空公司2，也就是承運航空公司進行討價還價博弈，確定最終轉讓價格，流程見圖1。

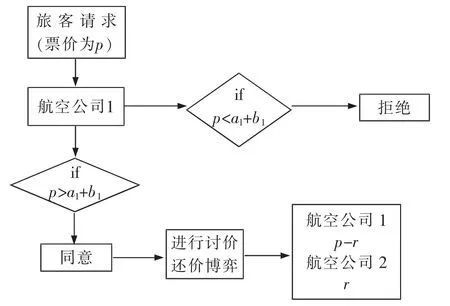
圖1 完全信息下的艙位轉讓流程Fig.1 Capacity transfer process with complete information

2 非完全信息下的討價還價模型

由于航空聯盟涉及到反壟斷法，以及技術上的欠缺，成員航空公司之間并不能完全信息共享，市場航空公司和承運航空公司不能知道對方的艙位等級、需求、以及當前的銷售數，需要改進完全信息下的討價還價模型。

2.1 參數說明

1）市場航空公司和承運航空公司可以通過銷售網站等途徑知道對方目前所開放的艙位等級的票價以及所在折扣。

2）市場航空公司與承運航空公司目前各自航段上開放的艙位等級的票價為a1′和b1′，市場航空公司認為b1′是承運航空最低期望收益，市場航空公司接受的價格區間為［b1′，p-a1］，承運航空公司接受價格區間為［b1，x1］，x1為承運航空公司認為市場航空公司所能承受的最大價格，x1=p-a1′；因此承運航空公司接受價格區間為［b1′，p-a1′］。

3）市場航空公司與承運航空公司當前預期收益為a1，b1，因為票賣出的概率小于1，所以b1′＞b1，a1′＞a1。

4）令ra′為市場航空公司認為談判成功的最優解，則ra′∈［b1′，p-a1］，rb′為承運航空公司認為談判成功的最優解，則rb′∈［b1，p-a1′］。

5）對于航空公司雙方怕失去旅客的程度，在上文中用客座率表示，在信息不完全的情況下，不知道相互航段當前的客座率，但可以用當前票價所在折扣預估當前的客座率，設為σ1′，σ2′（0≤σ1′≤1，0≤σ2′≤1），σ1′，σ2′越大，則當前票價折扣越高，怕失去該旅客的可能性越低。

2.2 模型建立

在不限次討價還價模型下，市場航空公司愿意支付給承運航空公司的價格ra′為

承運航空公司愿意接受的價格rb′為

由b1′＞b1，a1′＞a1，可得ra′＞rb′。若市場航空公司先出價ra′，ra′＞rb′，承運航空公司同意轉讓，此時市場航空公司支付的轉讓價格高于完全信息下。若承運航空公司先出價rb′，rb′＜ra′，市場航空公司也同意接受轉讓艙位，此時市場航空公司支付的轉讓價格低于完全信息下。由于是市場航空公司最后決定該票是否賣出，市場航空有權選擇利于自己的方式，讓承運航空先出價，那么市場航空公司的收益將高于完全信息下的收益。

3 非完全信息下的多階段議價模型

在市場航空不告知承運航空票價p為多少，并且互相不知道艙位等級、需求以及當前的銷售數，為了能夠解決不完全信息下有利于航空聯盟收益的票價被拒絕這一問題，建立多階段議價模型進行討論，該模型基于航空聯盟目前使用最多的按比例分配的基礎上，先在聯盟協議中確定基礎分配比例，再根據多階段議價模型確定最終轉讓價格。假設在航空聯盟中，博弈雙方都誠實守信，因為如果市場航空公司刻意降低轉讓價格，或承運航空公司刻意抬高轉讓價格，會使另一方的利益得到損害，并破壞聯盟的穩定性，一經發現會收到嚴重的懲罰。

3.1 議價步驟

實施動態議價的關鍵，在于兩點：一是市場航空公司確保所賣出的座位在聯盟網絡航線上可行，取決于市場公司所獲得的收益；二是承運航空公司是否同意接受市場航空公司旅客，主要取決于市場航空公司支付給承運航空公司的價格。

1）根據在航空聯盟協議中，收益分配比例確定為墜，1-墜。當市場航空公司收到一個票價為p聯運旅客的請求時，市場航空公司根據收益分配比例以及當前期望收益確定轉讓價格k1。

2）承運航空公司接收到轉讓價格k1之后，確定是否接受，若接受，結束；若不接受，向市場航空公司提出新的接受價格k2。

3）市場航空公司確定新提出的價格k2是否接受，若接受，結束；若不接受，向承運航空公司再次提出新的接受價格k3。

4）承運航空公司接收到新的轉讓價格k3之后，確定是否接受，若接受，結束；若不接受，則拒絕該票，結束。

3.2 模型建立

建立如下議價模型

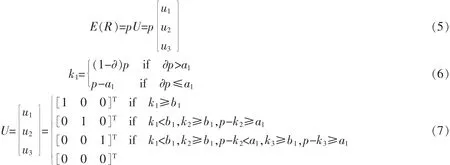
式（5）中E（R）為航空聯盟收益；U為議價結果；u1，u2，u3為議價階段決策變量，如果同意接受轉讓價格為1，否則為0。式（6）為市場航空公司確定首次轉讓價格，確保市場航空公司出售共同航段這張票的收益不比出售單獨航段票的收益少。式（7）為議價規則，其中a1，b1為市場航空公司和承運航空公司當前期望收益，保證了承運航空公司的收益也是大于或等于出售單獨航段的票。

該議價模型既可以保證有利于航空聯盟的票不被拒絕，又可以讓市場航空公司和承運航空公司的收益能夠大于或等于出售單獨航段的收益，使得聯盟更加穩定。

4 數據分析

聯盟內一家航空公司運用菲尼克斯（PHX）—芝加哥（ORD）的航線（Airline1），另一家航空公司運用芝加哥（ORD）—法蘭克（FRA）福航線（Airline2），可用座位分別為250座和200座，根據航空聯盟協議，航空公司協定好收益分配比例為40%和60%，航空公司加入航空聯盟前與加入航空聯盟后對于每個航段的票價和需求分別如表1所示。

根據EMSR方法，計算艙位分配如表2所示。

表1 兩家航空公司的票價與需求Tab.1 Fares and demands of two airlines’ODF

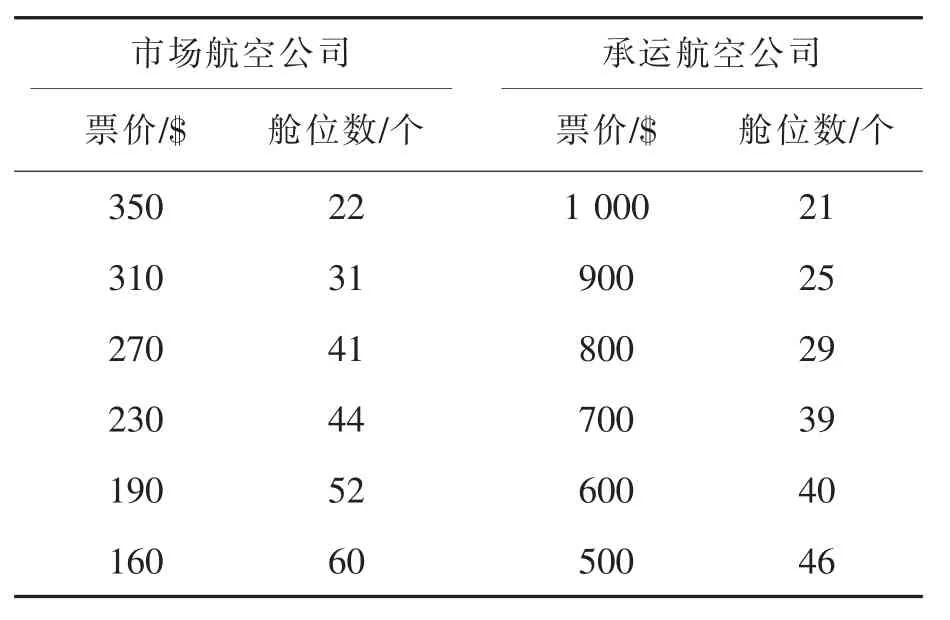
表2 票價等級和艙位分配Tab.2 Fare class and seat capacity allocation

選取任意5組銷售艙位組合下，市場航空公司的票價和期望收益見表3。

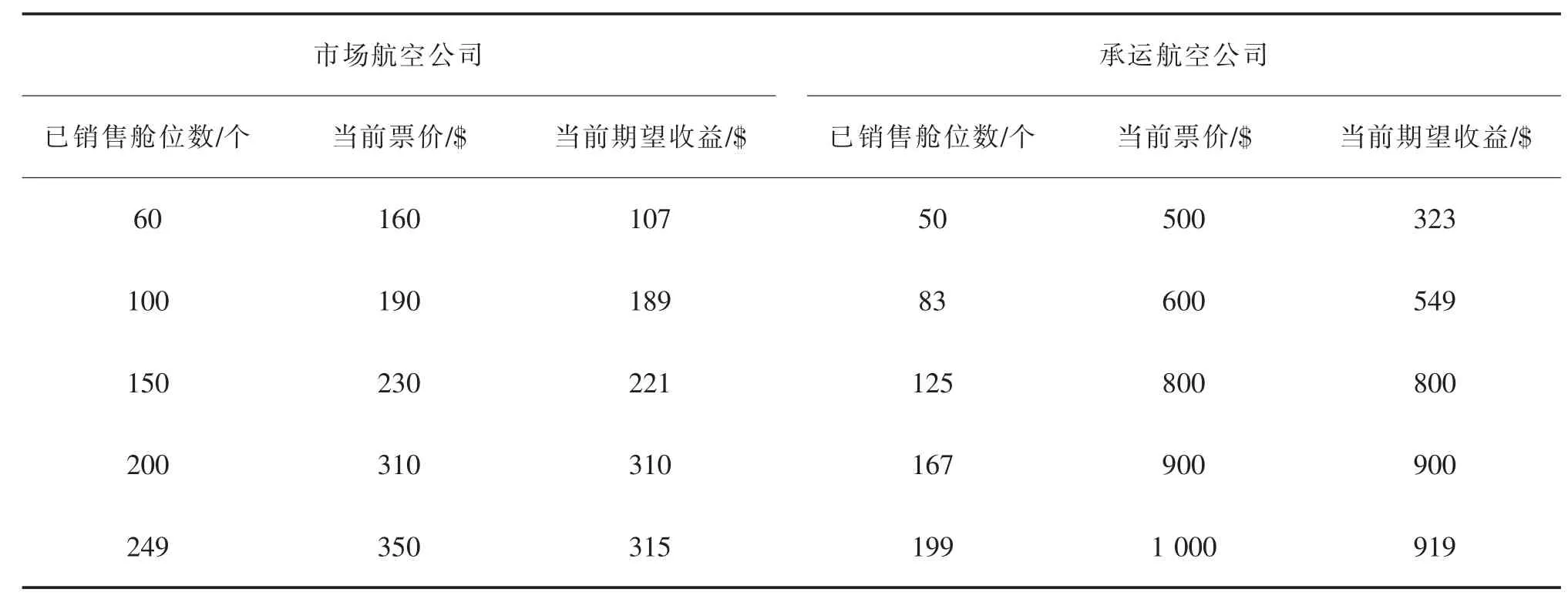
表3 已售艙位數及當前期望收益Tab.3 Capacity seat sold and expected revenue

根據公式分別計算出完全信息和非完全信息下的轉讓價格見表4和表5。

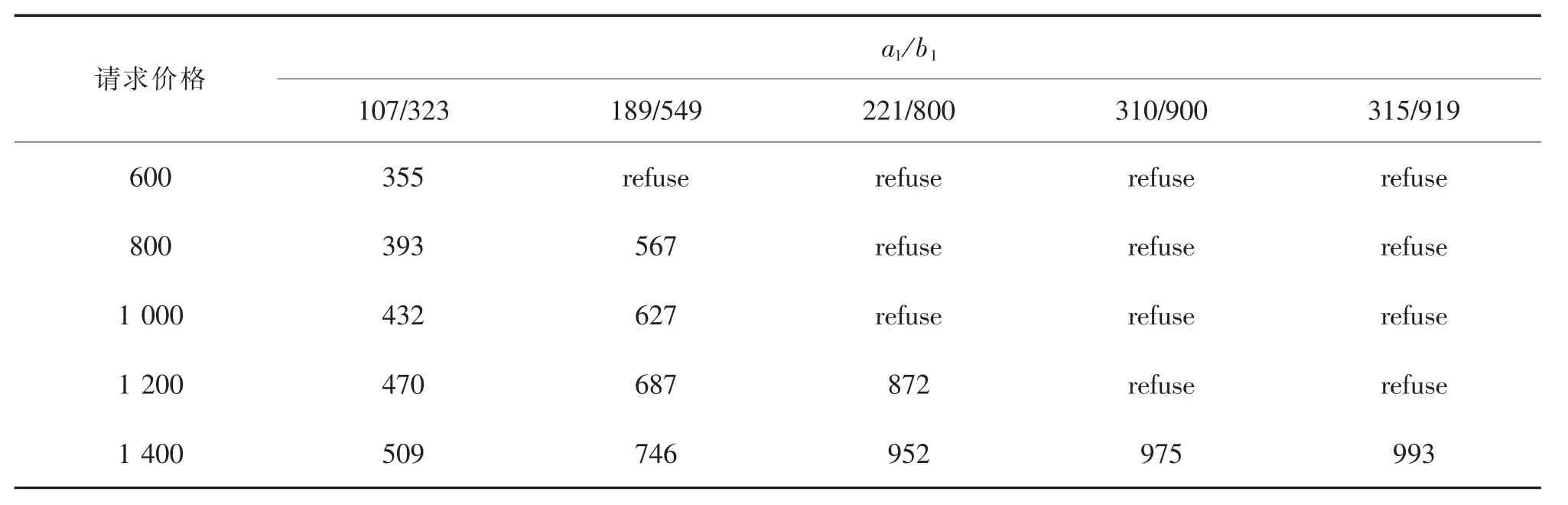
表4 完全信息討價還價下的轉讓價格Tab.4 Transfer price under complete information bargaining $

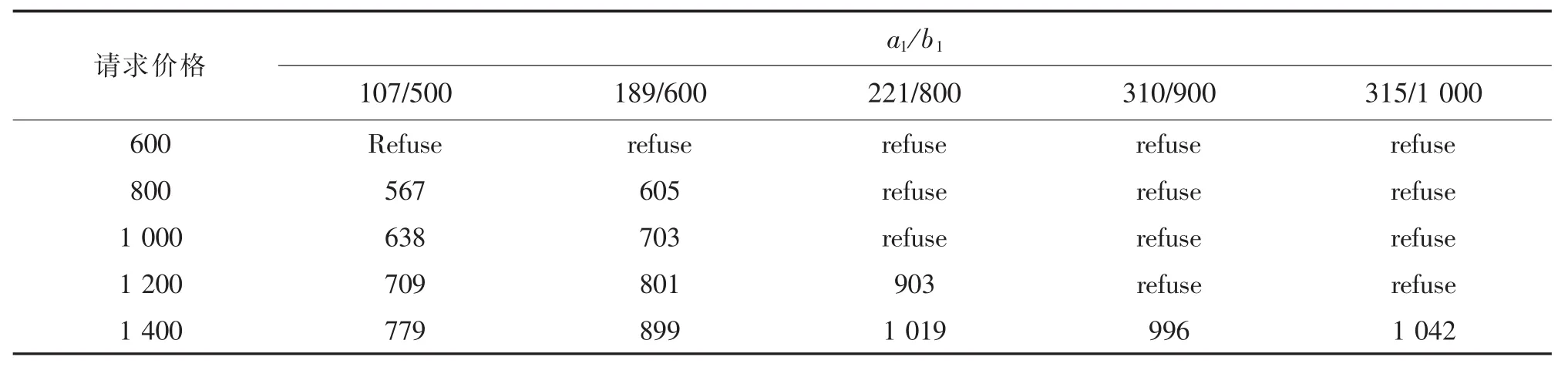
表5 非完全信息討價還價下市場航空公司先出價的轉讓價格Tab.5 Transfer price of the marketing airline under incomplete information bargaining $

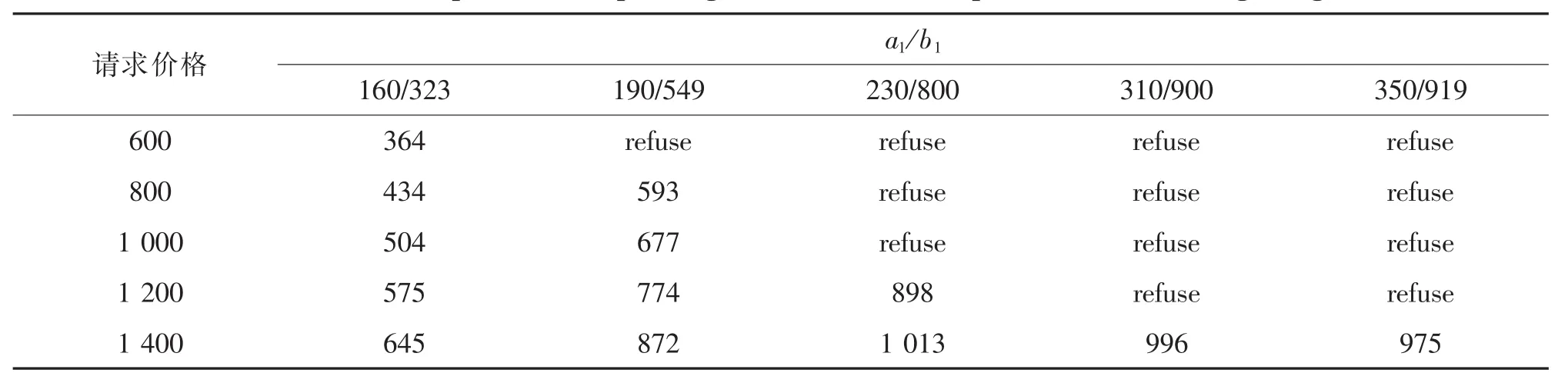
表6 非完全信息討價還價下承運航空公司先出價的轉讓價格Tab.6 Transfer price of the operating airline under incomplete information bargaining $

根據計算結果分析：在完全信息討價還價情況下，承運航空公司所獲得的轉讓價格最低，市場航空公司的收益比例最高；在非完全信息討價還價下，承運航空公司先出價，承運航空公司得到的轉讓價格較低，市場航空公司所得到的收益比例較高。可以說明在信息未知的情況下，市場航空公司由于不知道承運航空公司的情況，愿意出更高的轉讓價格“購買”承運航空公司的座位。對于承運航空公司來說，并不是知道的信息越多越好，在非完全信息下所獲得的轉讓價格反而更高。但是在非完全信息討價還價情況下，對于航空聯盟有利的票可能會被拒絕。見表7和表8。

表7 按比例分配收益Tab.7 Revenue sharing in proportion $

表8 非完全信息下多階段議價結果Tab.8 Revenue sharing of multi-stage bargaining under incomplete information $

比較表7和表8可以得出，多階段議價模型可以保證在非完全信息下，對航空聯盟有利的票不被拒絕，這改進了當前使用最廣泛的按比例分配方法，因為無論按照什么方法計算出的精確比例，都會存在這個問題。

5 結論

本文使用討價還價動態博弈模型，研究了完全信息下和非完全信息下市場航空公司所支付的轉讓價格，在完全信息下，所有對航空聯盟有利的票都會被接受，在非完全信息下，使用討價還價模型，會因為信息的不完全導致一部分對航空聯盟有利的票被拒絕。用討價還價方法得到的轉讓價格，是雙方博弈的結果，由于市場航空公司是機票銷售方具有最終決定權，因此在相同條件下對于增加部分收益分到的比例高于承運航空公司，除此之外，轉讓價格也跟航空公司的客座率相關，客座率越高，分到的比例越高，這可以激勵航空公司銷售。

建立的多階段議價模型，是基于航空公司目前使用最多的按比例收益分配的方式之上。在不違反反壟斷法的前期下，彌補了目前分配方式的缺陷，結果表明，多階段議價模型可以防止有利于航空聯盟的票被拒絕，并且保證各航空公司的利益不低于出售單航段票。

[1]BOYD A.Airline alliance revenue management：Global alliances within the airline industry add complexity to the yield management problem[J].OR MS Today，1988，25：28-31.

[2]WRIGHT C P.Dynamic revenue management in airline alliance[J].Transportation Science，2010：15-37.

[3]VINOD B.Alliance revenue management：Journal of revenue and pricing[J].Management Science，2005，4（1）：66-82.

[4]GRAF M，KIMMS A.Transfer price optimization for option-based airline alliance revenue management[J].International Journal of Production Economics，2013，9：281－293.

[5]QETINER D，KIMMS A.Assessing fairness of selfish revenue sharing mechanisms for airline alliances[J].Omega，2013，8：641－652.

[6]DE LA TORRE P E.Airline alliance：The airline perspective[R].London：Cambridge，Massachusetts Institute of Technology，Dept of Aeronautics and Astronautics，Flight Transportation Laboratory，1999：45－62.

[7]TOPALOGLU H.A duality based approach for network revenue management in airline alliances[J].Journal of Revenue&Pricing Management，2012，11（5）：500－517.

[8]WALDEMAR G，KIMMS A.Revenue management under horizontal and vertical competition within airline alliances[J].Omega，2015，6：1－28.

[9]PETER P B.Air travel demand and airline seat inventory management[D].Cam bridge：Massachusetts Institute of Technology，1987.

[10]LITTLEWOOD K.Forecasting and Control of Passenger Bookings[R].Israel：AGIFORS Symposium，1972：21-34.

[11]張秀敏，文曙東.基于投標價格法的鐵路客運收益管理方法改進[J].華東交通大學學報，2005，22（3）：63-66.

[12]蔣菱，王崢，黃仁樂，等.基于不完全信息下討價還價模型的動態聯盟利益分配研究[J].價值工程，2016（17）：231－234.

[13]詹文杰，鄒軼.基于演化博弈的討價還價策略研究[J].系統工程理論與實踐，2014（5）：1181－1187.

[14]杜少甫，朱賈昂，高冬，等.Nash討價還價公平參考下的供應鏈優化決策[J].管理科學學報，2013（3）：68-72.

[15]簡惠云，許民利.風險規避下基于Stackelberg博弈與Nash討價還價博弈的供應鏈契約比較[J].管理學報，2016（3）：447-453.

Research on Transfer Price of Airline Alliance Based on Bargaining Model

Gu Yingjing，Zhu Jinfu
（College of Civil Aviation，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China）

With the development of global economic integration and the deepening of aviation alliance,a major issue that needs to be addressed is how to share the revenue generated from selling tickets for products among the individual airlines.Through the theory of bargaining dynamic game,this paper analyzed the transfer price between marketing airline and operating airline with complete and incomplete information and established the multi-stage bargaining model of proportional distribution with incomplete information.The results showed that the transfer price based on bargaining game can encourage airlines to sell tickets,and marketing airlines yield high revenues with incomplete information.Conversely,operating airlines get higher transfer price with incomplete information than that of complete information.This model remedies the limitation of the existing distributive pattern,which may guarantee the enterprises’interest.

airline alliance;transfer price;dynamic game;bargaining model

F562

A

1005-0523（2017）03-0053-07

（責任編輯 姜紅貴）

2016－12－06

江蘇省博士生科研創新基金（KYLX_0292）

顧穎菁（1988—），女，博士研究生，研究方向航空聯盟收益管理。

朱金福（1953—），男，教授，博士生導師，研究方向為航空運輸最優化，不正常航班恢復。