模糊條件下配送中心選址評價方法研究
樓振凱,戴曉震
(溫州商學院管理學院,浙江 溫州 325035)
模糊條件下配送中心選址評價方法研究
樓振凱,戴曉震
(溫州商學院管理學院,浙江 溫州 325035)
在配送中心選址問題的背景下,從定性和定量兩個角度出發分析對比已有的選址評價方法,指出其適用對象。在此基礎上,結合指標對比關系的模糊性和指標數值的模糊性,對模糊條件下配送中心選址評價問題進行分類處理:模糊層次分析法確定指標對比關系模糊下的權重,并運用灰色綜合評價確定評價對象的優劣性;離差最大化法求得指標數值模糊下的權重,利用改進理想解排序法(TOPSIS)對評價對象按理想程度進行排序。并結合算例說明不同情形下方法的有效性和適用性。
評價方法;模糊指標;確定權重;灰色關聯度;離差最大化
作為供應商與客戶的橋梁,配送中心在物流系統中起著重要的承接作用。而配送中心的選址問題則是配送中心規劃與建設的關鍵一環,不僅決定了配送模式和配送距離,而且影響著整個系統的運作效率。關于配送中心選址的研究主要可以分為兩大類:一類是以數學規劃、智能算法為工具的節點尋找問題,通過建立選址模型求得理想節點;另一類是以評價模型為主的節點選擇問題,運用層次分析法、熵權法、理想解法等對備選地址進行篩選排序。
關于節點尋找問題,早期的研究中常用的模型和方法有混合整數規劃模型、鮑姆爾-沃爾夫法、逐次逼近模擬法等。后續的研究中,文獻[1]提出了基于軸不等式族的分支割平面法,在解決無容量限制的選址問題中取得滿意的效果;對于類似的問題,文獻[2]改進了半拉格朗日松弛算法,通過對偶上升算法尋找原始-對偶問題最優解;文獻[3]從圖論的角度出發,構建了加權動態圖的選址模型并通過實際案例分析了模型的合理性。然而,由于選址問題的實際約束大大多于理論約束,優化算法求得的理想解往往并不具有可行性,因此近幾年學者大多從對備選節點評價、排序的角度深入研究。文獻[4-9]分別從指標對比和指標數值的角度確定各指標的權重,并對指標數值進行標準化處理,從而得出每個備選節點的綜合評價值;文獻[10]考慮到熵權法片面地通過指標變化范圍確定權重的缺點,采用三角模糊數改進并取得了良好效果;文獻[11-13]分別從數據方差均值和歐氏距離的角度對灰色關聯度進行改進,提出改進的灰色綜合評價法解決選址問題。文獻[14]將特征值法和TOPSIS結合,求得備選點的綜合排序。
上述研究一定程度上解決了節點尋找和節點選擇問題。然而,現有文獻較少考慮到確定權重的時候指標重要性對比的模糊性以及指標數值本身的模糊性問題,而模糊性在現實問題中又普遍存在。本文在總結權重確定和備選點排序的評價方法的基礎上,對兩類模糊問題提出改進評價方法。對指標間對比關系模糊的問題,采用三角模糊數表示其決策矩陣,通過模糊層次分析確定權重,灰色綜合評價求得備選節點的優劣排序;對指標數值模糊的問題,采用離差最大化法確定指標權重,改進TOPSIS法對備選節點進行排序。
1 指標分析和方法比較
評價指標的選取取決于對選址影響因素的分析。對影響因素分析如下:
1)客戶信息分析。配送中心以提供給客戶更好的配送服務作為目標,對客戶信息進行分析是選址的首要任務,客戶信息分析的主要指標是客戶需求量以及客戶地理位置。現實問題中,地理位置一般是確定的,而需求量往往是模糊性指標。
2)交通便利性分析。配送活動包括裝車、運輸的過程,交通便利性越強,那么道路的通行效率相對越高,越便于車輛調度。
3)土地成本分析。配送中心建設成本是企業所關心的主要問題,選址位置的不同,直接導致土地使用成本的差異。
4)政策支持度分析。配送中心的建設和發展也離不開政策的支持,故應該考慮區域產業發展的情況。當地區域對物流的支持力度越大,往往獲得的優惠政策越多。
配送中心選址問題屬于多屬性決策問題,對多屬性決策問題的評價方法進行總結和比較如表1所示。
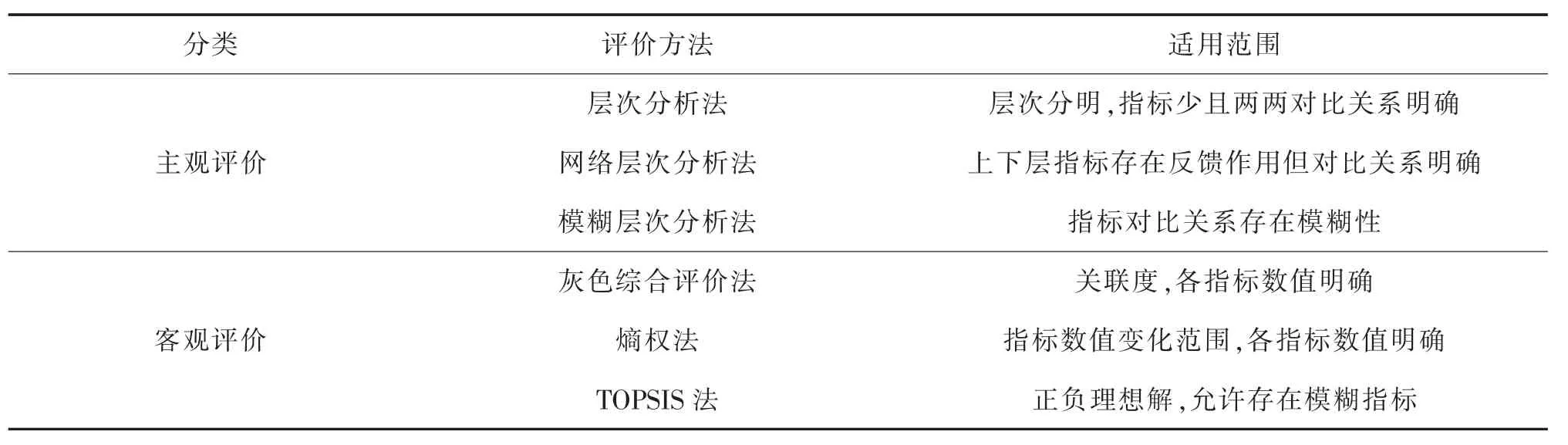
表1 評價方法比較Tab.1 Comparison of evaluation methods
在表1的方法中,各類層次分析、熵權法主要用于對指標權重的確定,灰色綜合評價和TOPSIS則解決評價對象的優劣排序問題。
2 對比關系模糊性問題
指標兩兩對比關系模糊,但指標數值確定的問題,給出模糊層次分析法確定指標的權重,并對指標數值標準化處理,構造參考數列,求各評價指標的關聯度并進行排序。
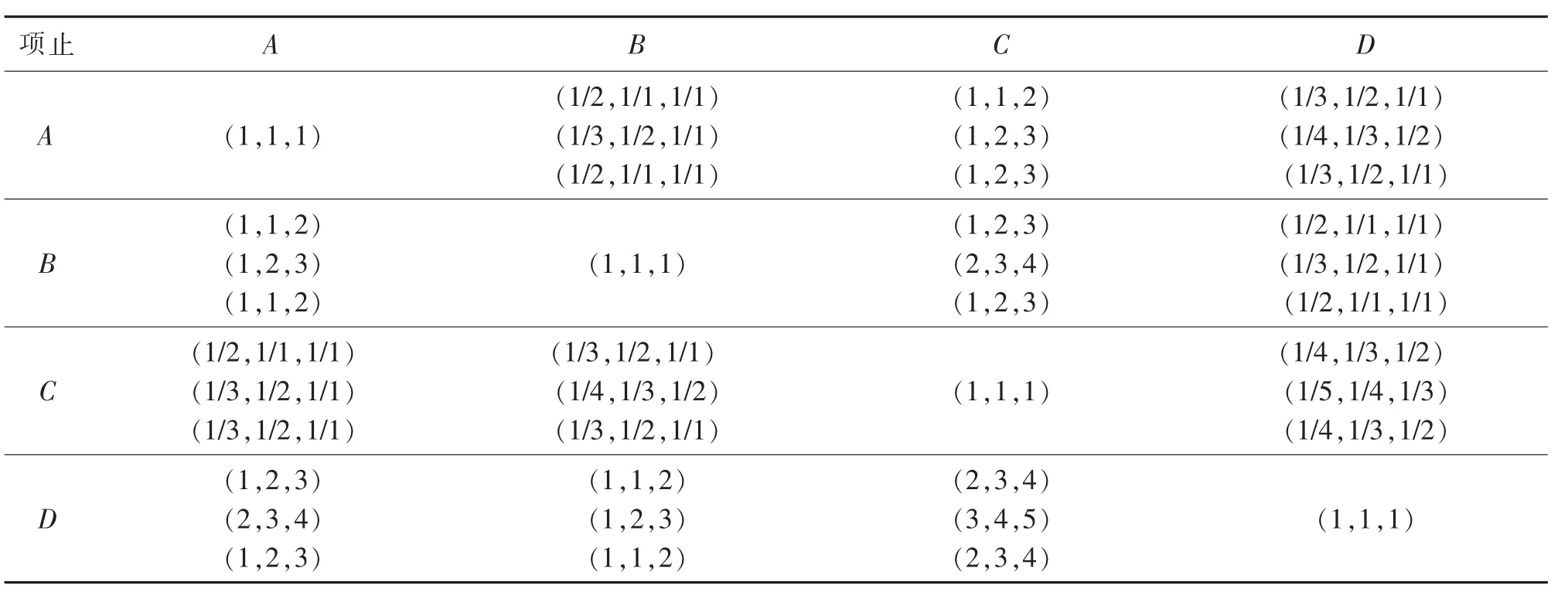
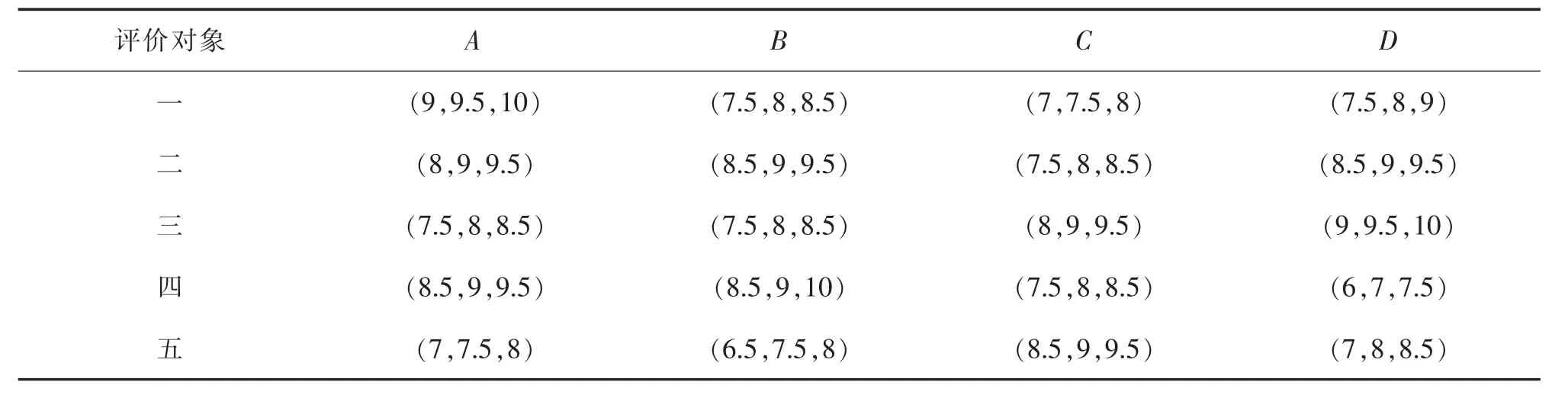
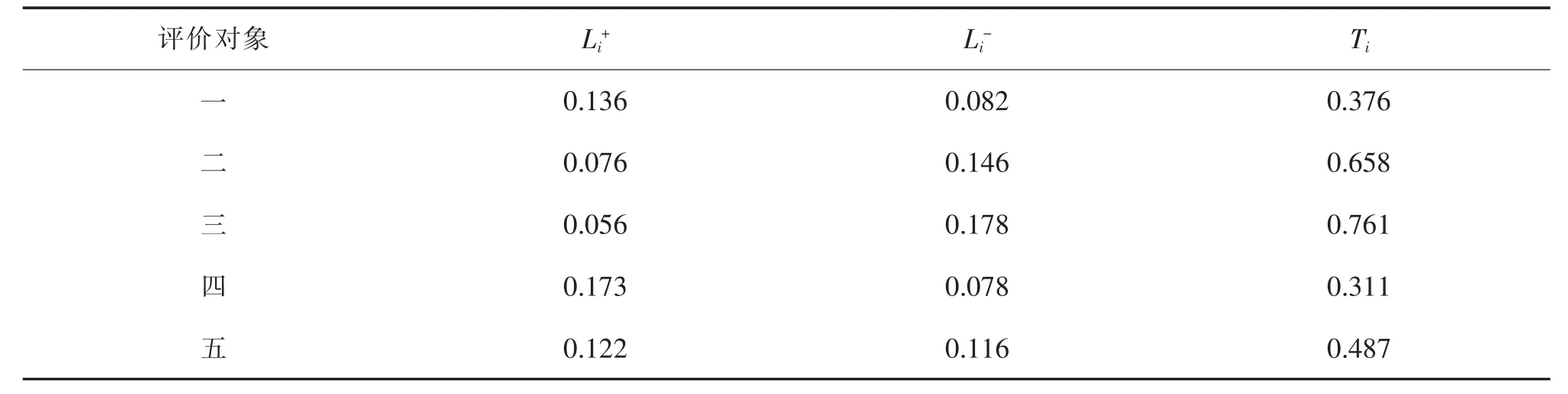
采用包括最低可能值、最可能值和最高可能值的三角模糊數作為專家評價的比較值。給出多個專家進行模糊打分情況下的模糊數整合規則。對于第i個評價對象在第j項指標上的測評值,n個專家模糊打分分別為X1=(a1,b1,c1),…,Xn=(an,bn,cn),其中ai 由介值定理可知,X仍然是一個三角模糊數。得到模糊決策矩陣A如下 式中:xmn表示整合的模糊值。計算指標i的模糊綜合值pi,按以下公式 得到各指標的模糊權重,最后通過模糊隸屬度函數去模糊化,并確定每個指標的權重P 將以上權重歸一化,得到各指標的主觀權重P=(p1,...,pn)。 灰色綜合評價的第一步是對指標數值進行同趨化和標準化處理,后者也稱無量綱化。對于效益型指標,將整列數值和其中最小值作比;對于成本型指標,取整列中最大值,和列中每個數值作比。灰色關聯分析常用的標準化處理有初值化和均值化,考慮到計算關聯度之前每個指標要乘上其權重,本文采用另一種同趨化和無量綱化同時處理的極差法,將指標數值規范在[0,1]之間。設評價指標數值矩陣Y=(yij)m×n,處理后的標準矩陣Z=(zij)m×n。 對于成本型指標 對于效益型指標 從加權標準化矩陣中選擇每個指標的最優值,組成參考數列。對于參考數列z0和比較數列zi,計算各指標對應的差的絕對值,記為Δmin和Δmax,則各評價對象各指標的關聯系數由以下公式確定 式中:ζ為分辨系數,根據序列的關聯程度選擇,一般取(0,0.5]。將每個評價對象各指標的關聯系數集中為一個值,也稱絕對關聯度ri,一般采用求平均數的方法 與之類似,加權關聯度Ri由以下公式確定 根據加權關聯度大小完成評價對象的優劣排序。與理想目標的關聯度越大,表示該評價對象的理想程度越高,在排序上也越優先。 很多時候指標數值無法確切給出,只能確定其范圍、程度,這類問題歸納為指標數值模糊性問題,這類問題同樣可以分成計算權重、評價對象排序兩個步驟。對于權重的計算,同樣可以通過層次分析法、模糊綜合評價等求得,然而主觀判斷獲得的比值有其難以克服的缺陷,本文結合模糊指標的特點,給出離差最大化法的權重客觀求法。在方法原理上,熵權法從指標數值變化范圍所反映的信息熵出發,確定各指標的權重;離差最大化法同樣以指標偏差大小為依據,以拉格朗日函數求得權重。給出離差最大化法計算過程。在獲得權重的情況下運用TOPSIS法計算評價對象到正負理想解的距離以及相對貼近度,并按貼近度的大小對評價對象進行優劣排序。 以三角模糊數表達指標數值,uij=(aij,bij,cij),則uij和ulj之間的歐式距離為 式中:qj為權重。運算遵循三角模糊數四則運算法則。離差最大化模型表達為 構造拉格朗日函數可求得 確定了指標權重,可以運用改進TOPSIS法對備選點排序。 步驟1:規范化決策矩陣。規范化的目的同樣是為了同趨化、歸一化,對正向指標和負向指標分開處理。對于三角模糊數,當指標屬于正向指標時 當指標為負向指標時 式中:λmaxj為每個指標的最大值;μminj為每個指標的最小值。 步驟2:確定加權規范化決策矩陣W 步驟3:確定正理想解I+和負理想解I-,其中模糊數的比較采用均值法 步驟4:計算第i個評價對象到正負理想解的歐式距離 步驟5:計算每個評價對象與理想目標的相對貼近度Ti 4.1 算例1 某地計劃新建一個配送中心,現有五個備選地址可供選擇,考慮的指標為土地成本、需求量、交通便利性和政策支持度等,這其中有準確數值、評分、百分比等,記為A,B,C,D。數據見下表。 表2 評價原始數據Tab.2 Original evaluation data 標準化數據之前,先確定各指標權重。利用三角模糊數來表達決策偏好。三位專家的打分表如下。 表3 模糊判斷矩陣Tab.3 Fuzzy judgment matrix 各指標權重P=(0.22,0.29,0.11,0.38)。標準化矩陣如表4所示,其中零為參考項。 表4 標準化矩陣Tab.4 Standardized matrix 求得各備選點的加權關聯度為(0.465,0.670,0.707,0.570,0.635)。可以看出,各備選地址的優劣順序為三,二,五,四,一。 4.2 算例2 同樣有5個備選地址,考慮的指標為土地成本、需求量、交通便利性和政策支持度。現實問題中,在投入運營之前無論哪個指標都無法給出確切數值,只能給出程度范圍,存在語言值向數值轉化的過程。因此用模糊性指標表達較符合實際,本文采用三角模糊數。基于偏好信息的專家打分如表5所示。 表5 模糊判斷矩陣Tab.5 Fuzzy judgment matrix 離差最大化法求得權重Q=(0.25,0.23,0.19,0.33),標準化處理后的加權決策矩陣如表6所示。 表6 加權決策矩陣Tab.6 Weighted decision matrix 由式(17),式(18)可得正負理想解為 由式(19),式(20)以及正負理想解計算各備選地址到正負理想解的歐式距離及相對貼近度,數據見表7所示。 表7 相關距離及貼近度Tab.7 Correlation distance and closeness degree 由理想解法貼近度大小排序知,備選地址的優劣排序為三,二,五,一,四。 配送中心選址的優劣對企業物流系統運作成本、效率有著深遠影響,而基于優化算法的節點尋找往往不能滿足實際問題的諸多定性約束。對備選地址進行分析、比較和評估,從中選擇最理想的地址作為配送中心的節點選擇問題引起更多關注和研究。 選址評價問題中,往往存在模糊性因素。本文將模糊選址評價問題分為兩類,即指標對比關系模糊性問題和指標數值模糊性問題,分別給出模糊層次分析法-灰色綜合評價法和離差最大化法-TOPSIS法,對兩類問題提供了可行的解決方法。算例分析表明,改進的評價方法具有可行性和適用性。文章的不足之處在于,沒有對主觀評價和客觀評價的優劣程度給出評判準則,后續的研究還可以對主客觀權重的平衡、指標數較多且相互關聯的問題展開研究。 [1]安邦,程朋.基于分支割平面的一類無容量限制設施選址問題求解算法[J].運籌學學報,2015,19(4):1-13. [2]張慧珍,魏欣,馬良.求解無容量設施選址問題的半拉格朗日松弛新方法[J].運籌學學報,2015,19(4):37-47. [3]劉欣.物流園區選址模型中的動態Voronoi圖問題及評價[J].價值工程,2015(21):168-169. [4]王曉博,李一軍.電子商務環境下物流配送中心選址模型與評價方法[J].系統管理學報,2006,15(3):199-204. [5]許德剛,肖人彬.基于智能優化的糧食物流中心選址評價體系[J].河南工業大學學報,2009,30(6):80-83. [6]劉謖汾,馬斌.煤炭物流園區多目標動態選址[J].工業工程,2015,18(6):110-115. [7]孔令明,王云峰.基于可拓層次分析法的物流中心選址評價[J].技術經濟與管理研究,2009(6):25-27. [8]田時中,趙鵬大.中部六省霧霾壓力動態綜合評價模型與實證[J].統計與信息論壇,2016,31(9):56-61. [9]王海濱,陳延君.物流配送中心選址的熵權法綜合評價研究[J].哈爾濱商業大學學報,2010(4):61-64. [10]遲國泰,王鈺娟,劉艷萍.基于三角模糊熵的經濟評價模型及副省級城市的實證研究[J].運籌與管理,2010,19(5):107-117. [11]陳戰波,黃小舟.物流配送中心選址的改進灰關聯度評價方法[J].統計與決策,2015(3):52-55. [12]朱清香,曹秋芳,劉晶.基于改進灰色關聯的商業網點最優選址研究[J].統計與決策,2016(8):51-53. [13]DYMOVA,PAVEL S,ANNA T.An approach to generalization of fuzzy TOPSIS method[J].Information Science,2013(238):149-162. [14]楊磊,黃曉燕.物流配送中心選址的設計及評價模型[J].統計與決策,2008(9):80-81. [15]趙萬華.區域物流配送中心選址的評價方法研究[D].武漢:武漢大學,2011. [16]王森,魏旭穎.基于模糊模型的網絡社會場系統的安全評估[J].華東交通大學學報,2016,33(5):132-138. Study on Evaluation Methods of Distribution Center Location under Fuzzy Condition Lou Zhenkai,Dai Xiaozhen Aiming at the distribution center location,this paper compared the existing location evaluation methods and discussed their applications from the two perspectives of qualitative and quantitative analysis.Combining the fuzziness of the indexes contrast relationship with the fuzziness of the indexes value,it classified and solved the evaluation problems of distribution center location under fuzzy conditions:fuzzy analytic hierarchy process was used to determine the weight of indexes for the fuzzy contrast relationship,and the grey comprehensive evaluation was applied to determine the superiority and inferiority of evaluated objects;the weights of fuzzy indexes was obtained by maximizing deviations,and improved TOPSIS method was adopted to rank the evaluated objects according to the ideal level.Finally,it illustrated the effectiveness and applicability of the evaluation methods under different circumstances through numerical examples. evaluation method;fuzzy index;weight decision;grey correlation degree;maximizing deviations F252 A 1005-0523(2017)03-0081-07 (責任編輯 姜紅貴) 2016-12-01 樓振凱(1989—),助教,碩士,主要研究方向為物流管理。








3 指標數值模糊性問題




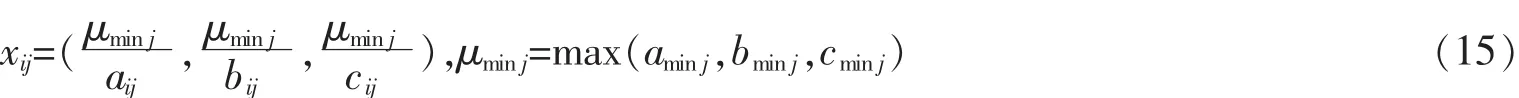

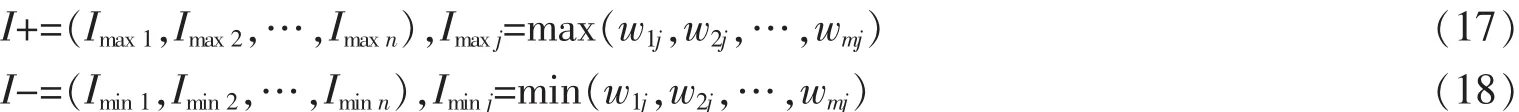


4 算例分析




5 總結
(School of Management,Wenzhou Business College,Wenzhou 325035,China)

