基于黃金分割遺傳算法的VISSIM仿真模型參數校正

楊文臣，張 輪，王 錚，胡澄宇

（1.云南省交通規劃設計研究院陸地交通氣象災害防治技術國家工程實驗室，云南 昆明 650031；2.同濟大學道路與交通工程教育部重點實驗室，上海 201804）

基于黃金分割遺傳算法的VISSIM仿真模型參數校正

楊文臣1，2，張 輪2，王 錚2，胡澄宇1

（1.云南省交通規劃設計研究院陸地交通氣象災害防治技術國家工程實驗室，云南 昆明 650031；2.同濟大學道路與交通工程教育部重點實驗室，上海 201804）

微觀交通仿真模型的準度直接決定所模擬交通場景的真實性。提出一種黃金分割遺傳算法的VISSIM仿真模型參數校正方法。首先，詳細梳理了VISSIM仿真的標準作業流程及模型參數的校正原理；接著，設計了以通過量為指標的目標函數和仿真參數個體的離散化方法；然后，采用黃金分割遺傳算法具體設計了VISSIM模型參數的校正方法；最后，以典型城市信控路口為例，分析參數校正后的仿真模型特性，并采用實測路口轉向流量數據驗證所提出參數校正算法的效用。

微觀交通仿真;參數校正;黃金分割遺傳算法;參數離散;VISSIM

微觀交通仿真軟件能對單一車輛行駛行為進行微觀處理，模擬、分析和評價實際道路上交通流的運行，是交通系統管理與控制的重要實驗工具[1]。作為一種無偏的可視化評價工具，VISSIM、PARAMICS、CORSIM等仿真軟件現已廣泛應用于交通流特性分析、交通控制方法驗證、交通設計方案評價、駕駛行為分析等智能交通領域的應用研究[2-3]。然而，當前主流交通仿真軟件的默認模型參數均源自國外交通流狀況的標定結果，這往往與我國城市道路的現實交通流特征不符。為確保交通仿真結果的可信度，必須采用實際數據標定仿真模型的參數，以建立精細化的仿真模型[4-5]。

仿真參數校正實質上是一個離散數據尋優的過程，遺傳算法模擬生物自然進化過程，從問題解的種群開始全局搜索，現已被廣泛應用于仿真模型參數校正。CHEU等構建了一個快速路系統FRESIM模型，并最早將遺傳算法應用于仿真參數校正[6]。LEE等以交通流量及占有率為指標，采用遺傳算法校正PARAMICS模型的車頭時距與平均反應時間[7]。PARK等采用階段式的校正策略提出一種基于遺傳算法的參數校正流程，并在CORSIM、PARAMICS與VISSIM中進行了驗證[8]。李志明等選取VISSIM的6項模型參數，以進口道延誤為指標，采用遺傳算法校正仿真參數[9]。孫劍等以行程時間和流量為指標，采用遺傳模擬退火啟發式算法對8類VISSIM仿真模型進行參數校正[10]。周素霞以路網車輛總數為評價指標，采用遺傳算法對2類VISSIM仿真模型參數校正[11]。唐少虎等以進口排隊長度為目標，采用人工螢火蟲算法校正了7類VISSIM仿真模型參數[12]。眾多學者已將遺傳算法應用于仿真模型參數校準問題，并已在校準流程、算法設計、實驗驗證等方面積累了較好的基礎。然而，既有研究多數缺乏VISSIM仿真參數校正機制及校正參數物理意義的詳細解析，且多數參數校正的研究考慮Wiedemann跟車模型參數，而較少系統地考慮跟馳、換道參數；同時，簡單遺傳算法容易陷入局部最優，雖然采用啟發式的混合群體智能算法能增強遺傳算法局部優化能力，但這類算法局部尋優計算相對復雜，較大限制了參數優化效率。

本文系統解析VISSIM模型參數校正的機理及模型參數的選取，并以實測路口流量數據為基準定義評標目標函數，引入黃金分割算子進行局部尋優，設計了基于黃金分割遺傳算法的VISSIM模型校正流程[9]。以典型城市信控路口為例，對比分析實測/仿真轉向流量數據，以及校準前/后平均停車間距等9個仿真模型參數，驗證提出算法的效用。

1 VISSIM仿真模型校正

1.1 交通仿真標準作業流程

微觀仿真應用的標準作業流程如圖1所示，包括3部分：交通基礎路網建模、交通流建模和智能交通仿真應用。基礎路網建模對基礎路網幾何設施和交通控制設施等進行可視化建模，配置路網OD和統計分析參數等。交通流建模通過仿真模型參數的校準實現，旨在使仿真模型最大程度地逼近現實道路交通流的運行狀況。為有效支持交通運營分析，智能交通仿真應用針對交通設計、管理與控制等應用問題展開具體評價、驗證及優化。可見，交通仿真軟件的建模精度直接決定著仿真結果的可信度。但是，實際工作中的許多交通仿真應用并不重視仿真模型參數校準。

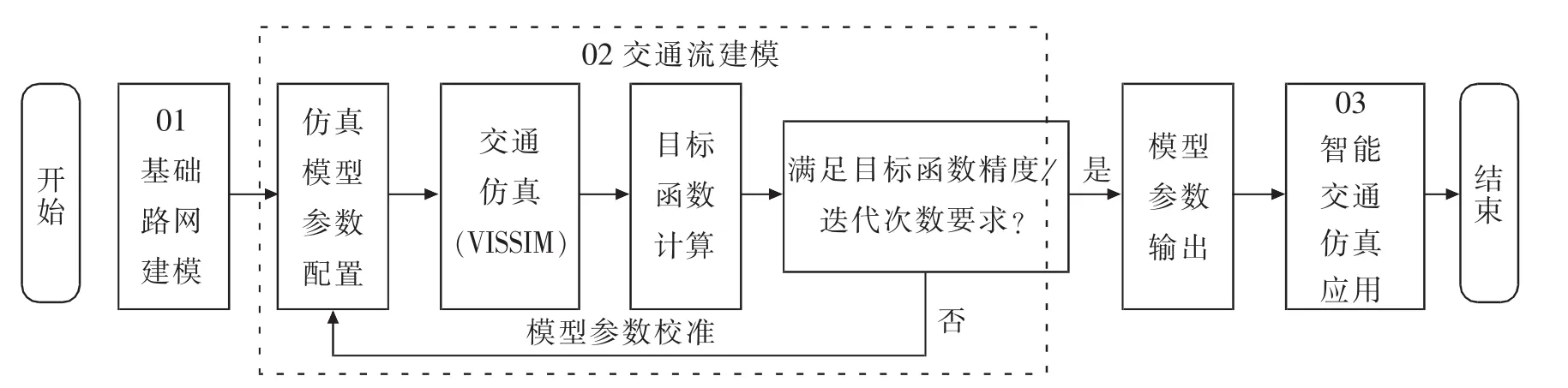
圖1 微觀交通仿真應用的標準流程Fig.1 Genetic process of microscopic traffic simulation application

1.2 參數校正機制

VISSIM交通仿真的交互機制如圖2所示，包括3部分：用戶、輸入/輸出接口、VISSIM仿真軟件[13]。用戶負責基礎路網的可視化建模和交通控制程序的二次開發；在用戶配置好交通控制環境后，控制程序作為外部程序獨立運行，采用輸出接口檢測交通數據，并采用相應的算法優化控制方案，進而通過輸入接口返還至VISSIM仿真軟件。VISSIM仿真器負責道路交通場景的模擬、交通數據的采集和控制方案的執行。輸入/輸出接口負責VISSIM仿真器與控制程序之間的實時數據交互，共有3種接口的開放機制，包括COM組件式對象接口函數、原始模型文本讀寫 （VISSIM的.inp模型文件）、DLL動態鏈接庫（數據交互）。

1.3 仿真模型參數

微觀交通需校準顯著影響路網通行能力、駕駛行為特征和車輛性能的參數。VISSIM城市道路模型是在Wiedemann 1974“生理-心理跟馳模型”的基礎上演化形成的[13]，開放的模型參數主要包括：跟馳行為、換道行為、優先規則、期望車速、加減速特性等5類。大量研究成果[1,4,8,12]表明，跟馳行為和車道變換是底層仿真模型的核心參數，必須進行校正；路網通行能力和車輛性能對優先規則、期望車速、加減速特性等對參數敏感，在進行場景的精細化建模時，需要正確配置。在信號控制路口，駕駛員嚴格按照信號燈色的有序通行，此時優先規則對通行能力的影響小，期望車速通常根據城市道路限速值采用“S”型速度分布進行標定。綜上分析，從城市道路駕駛行為和通行能力的角度出發，研究對Wiedemann 1974底層模型及跟馳、換道模型的9個參數進行校正，各參數的說明如表1所示

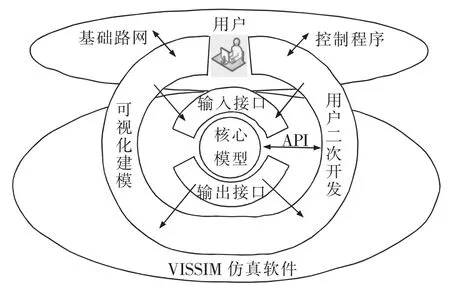
圖2 VISSIM交通仿真的交互機制Fig.2 The mechanism of VISSIM simulation modeling

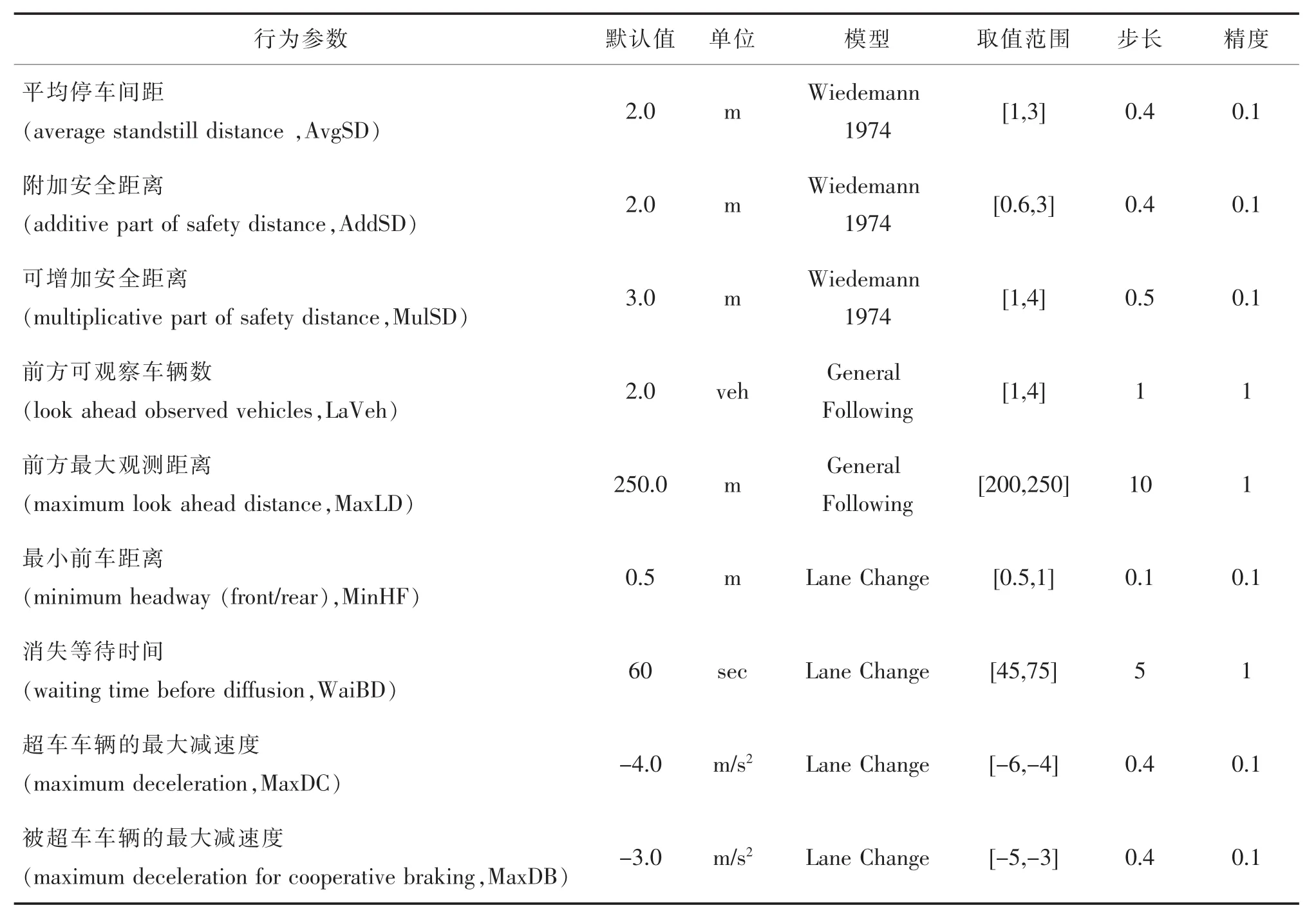
表1 城市道路VISSIM校正參數集及說明Tab.1 The VISSIM parameter set of urban road simulation model

表1中，平均停車間距、附加安全距離和可增加安全距離描述跟馳過程中兩停車車輛的平均停車距離和安全距離。前后車輛間的最小前車距離是影響道路通行能力及排隊長度的關鍵參數。前方可觀察車輛數及前方最大觀察距離決定駕駛員對環境的感知能力，可使駕駛員提早做出判斷。前車/后車最大減速度影響車輛的換道行為。在交通流量較多或配時方案不合理的條件下，處于分流點而不能順利換道的車輛顯著影響路口通行能力，消除前的等待時間決定了車輛等待變換車道空擋的最長時間。

2 仿真模型校正的算法設計

2.1 目標函數設計

平均絕對相對誤差（mean absolute percent error，MAPE）是衡量仿真效果準確性最重要的指標之一，直接反映整體的仿真準確性程度，MAPE的值越大，時段內的仿真誤差就越大；反之，仿真誤差就越小。以路口各流向通過車輛數的最佳匹配為目標，定義式（1）的MAPE函數來評價仿真模型的精度

式中：n為路口流向總數量，qir為斷面實際通過流量，qis仿真斷面通過流量。各流向的通過量采用布設在路口停前線前的線圈檢測器進行采集。

2.2 黃金分割遺傳算法

傳統的遺傳算法在求解時優化速度慢，且容易陷入局部最優，降低了尋優的速度與精度。對多約束的最優化問題，為克服遺傳模擬退火等混合算法的計算量大等不足，研究引入黃金分割比例確定局部最優點的搜索位置。黃金分割遺傳算法的具體描述和應用于交通控制問題的性能分析已在先前研究得到驗證[14-15]，其基本思想是：兩個局部最優個體將趨同于解空間的同一個“凹處”，因而，在兩個局部最優個體的基因之間，存在潛在的更優的基因位置。其局部尋優的計算原理如圖3所示。A和B為兩個相鄰的最優個體，C和C′為通過黃金比例得到的潛在最優點的位置，AC和AB、C′C和C′B的關系滿足黃金分割點定義。

圖3 黃金分割局部最優點的計算示意Fig.3 The illustration of golden-ratio based local optimal sets

2.3 仿真模型參數的離散化

表1中平均停車間距等6個仿真模型參數是連續的數值，且各參數的值域不同，連續型參數組合構成的取值空間在理論上是無限的。在數量有限的迭代次數內，巨大的取值空間將為最優模型參數的帶來顯著的不確定性，增加計算算雜度且容易限入局部最優。為降低群體搜索參數的復雜度，需對模型參數的數據進行離散化處理，以將大空間范圍內的參數數值離散為數量有限的幾個分級，原理如下：記模型參數i的值域為［li，ui］，優化步長為△Si，則參數i的分級數量Mi=（ui-li）/△Si。研究采用模型參數的離散化取值生成初始種群，1個個體表征9個模型參數的1種可能組合。記參數i的離散化取值為k，k是整數且k∈［0，Mi］，則參數i的第k個分級水平對應的實際參數值采用式（2）計算

2.4 算法校正步驟

基于黃金分割遺傳算法 （golden-ratio genetic algorithm，GRGA）的VISSIM模型參數校正的流程如圖4所示。整個過程采用GRGA進行參數群體的迭代尋優，對每一個可行的參數個體，在對應的交通仿真結束時計算其目標函數，以評價個體優劣。主要步驟如下：

步驟1：初始化。初始化遺傳算法和黃金分割算法的控制參數，并采用實數編碼生成初始種群PA和PB，其中，PA表示全局尋優種群，PB表示局部尋優種群，初始種群需滿足個體間互不相同準則，并預先加入已有文獻中的優秀個體。在算法參數中：進化代數Gen取100，PA種群規模Na取50，黃金分割尋優規模m取10，PB子種群規模Nb為2 m；MAPE的誤差為ρ；交叉和變異概率隨進化代數及適應度值自適應地動態調整[16]。

步驟2：VISSIM仿真及評價。對種群PA和PB中的新增參數個體，通過修改Vissim模型的.inp文件的參數，并采用COM接口調用VISSIM仿真函數運行一次仿真，在仿真結束時，根據統計的各流向轉向流量，計算個體的目標函數，即適應度。

步驟3：算法終止的判斷。如果適應度值滿足收斂條件或迭代次數達到預設的最大值，輸出最優的模型參數，反之進入下一步。

步驟4：采用Metropolis準則概率接受局部尋優種群PB的新個體，用接收的優秀個體依次替換種群PA最差的個體。

步驟5：局部尋優操作：為保持種群的多樣性，在簡單GA算法的每一新生代PA中，挑選最好的2 m個個體更新子種群PB，并從PB中隨機選取m個優秀個體作為初始向量，調用黃金分割算子強化遺傳算法（式1）的局部尋優搜索，更新局部尋優種群PB。

步驟6：遺傳算子操作[16]：采用“選擇、交叉和變異”算子全局優化種群PA，并轉向步驟2。

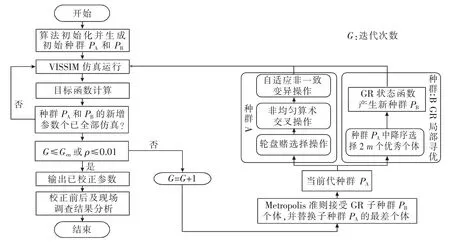
圖4 基于GRGA算法的VISSIM參數校正流程Fig.4 The calibration framework of VISSIM parameter based on GRGA

3 實例驗證

3.1 案例描述

選取深圳市某典型交叉口作為算法的驗證對象。此路口南鄰深圳市政府、北接北環大道，鄰近路段限速60 km/h，是深圳市關鍵交叉路口，具有交通設計規范、交通流量大等特征。路口采用多時段定時控制方案。該路口基礎路網、道路交通組織，以及標準四相位方案的VISSIM仿真模型如圖5所示，交叉口進口引道拓寬，且右轉交通渠化（不受信號燈控制）；采用一個月內路口感應線圈在順暢和擁擠狀態下實測交通量的均值作為狀態下交通需求OD，各流向的到達流量呈非均衡分布。

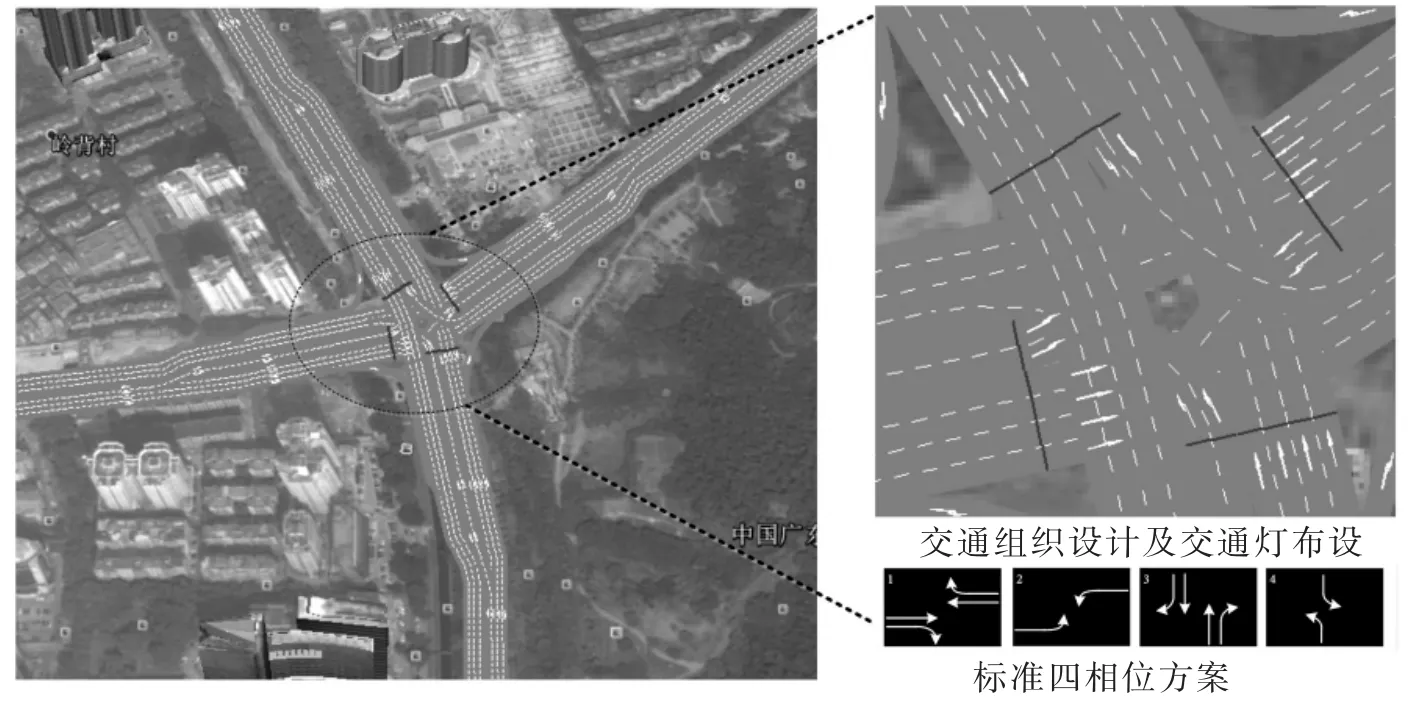
圖5 深圳某典型信控路口VISSIM仿真模型Fig.5 The VISSIM simulation model of a signalized intersection in Shenzhen

3.2 實驗設計

實現場景：①采用路口感應線圈在順暢和擁堵兩種狀態下的實測車流量的均值作為狀態的駛入流量（如表2示），仿真時長為2 h；② 為模擬路口短時交通流到達波動特性，根據線圈統計結果，在VISSIM的Routes文件中設置1 h內10 min間隔車輛的發車比例；③GRGA算法的每個個體決定每次仿真的9個模型參數。

實驗平臺：采用C#語言在Visual Studio 2010的.NET框架平臺上實現VISSIM仿真參數校正系統。受限于VISSIM 4.30的仿真實驗條件，研究采用文本讀寫的技術實現駕駛行為參數的校準，采用COM接口函數技術實現外部程序與VISSIM仿真交通數據和操作交互。

3.3 結果分析

1）校正后的模型參數。校正后的模型參數如表2所示。與表1默認的模型參數相比，平均停車間距(AvgSD)、附加安全距離(AddSD)、可增加安全距離(MulSD)減小達50%以上，消失等待時間(WaiBD)減小達25%，前方可觀察車輛數(LaVeh)增加1倍，超車/被超車車輛的最大減速度(MaxDC、MaxDB)增加50%以上，最小前車距離(MinHF)稍有增加，而前方最大觀測距離(MaxLD)不變。在校正后的參數中，AvgSD，AddSD以及MulSD三個值均明顯小于默認值，這表明與國外默認駕駛行為相比，校調后的駕駛行為更傾向于冒險，這與當前我國駕駛員的普遍侵略性駕駛習慣相符。

表2 校正后的VISSIM模型參數Tab.2 The calibrated parameters of VISSIM simulation model

2）各轉向小時交通量。模型參數校正前/后各轉向流量與現場實測觀測值的統計結果如表3所示。整體而言，仿真通過量均比實測通過量要小，這是因為研究以停車線前檢測線圈采集的通過量作為仿真輸入OD，有部分車輛仍在路段上離散行駛或在信控路口等待排隊。

表3 參數校正前/后各轉向的小時通過量Tab.3 The direction throughput before/after parameter calibration

在兩種交通狀態下，模型參數校正前/后各轉向流量絕對誤差的直觀描述如圖6示。在順暢狀態下，由于信控交叉口到達車流量較小，交通流干擾小，參數校正前/后駕駛行為的差異對各流向通過量的影響小，與校正前相比，校正后的MAPE減小了僅1.5%。在大流量的擁堵狀態下，對默認的模型參數，進口道小時通過量明顯失真，南進口直行流向的最大MAPE達17.9%；而校正后的結果與實測值相近，MAPE約為2.5%，與校正前相比，校正后的MAPE減小達16.5%，南進口直行的通過量顯著增加了400多輛。這是因為實驗路口各流向到達呈非均衡分布，交通強度最大的南進口左轉和直行車輛間跟馳換道行為頻繁，尤其在擁堵的交通條件下，受左轉排隊長度溢出專用展寬車道的影響，直行車輛因左轉車輛的阻擋不能順利通過，造成斷面變化區域的交通中斷，大幅減小了進口通過量。校正參數后，平均停車距離及附加安全距離的減小和前方可觀察的車輛數增加使得仿真車流中車間距減小，而減小的消失等待時間明顯降低溢出車輛的影響時間，這大幅提高了大流量進口的通過量。

圖6 模型參數校正前（-）后（+）各轉向流量絕對誤差Fig.6 The absolute error of throughput before and after parameter calibration

4 結論

在系統梳理VISSIM交通仿真作業標準流程、參數校正機制和仿真模型參數的基礎上，從減小混合遺傳算法局部尋優計算量的角度出發，本文引入黃金分割遺傳算法并設計了一種VISSIM仿真模型參數校正的算法，以典型城市信控路口為例，對仿真模型的9個參數進行校正。參數校正前/后仿真結果與實測數據的分析結果表明：采用黃金分割遺傳算法校準后的仿真模型更能描述實際的交通情況，且VISSIM仿真參數對交通流的運行狀況的影響在一定程度上與交通流的強度相關。這主要體現在中低流量的交通流條件下，不同行為參數間路口各流向通過量的差異不顯著，但是，在中高流量條件下，因行為參數差異導致的交通運行狀況的偏差很大，必須進行參數校準。

[1]鄒智軍.新一代交通仿真技術綜述[J].系統仿真學報，2010，22（9）：2037-2042.

[2]KOTUSEVSKI G，HAWICK K A.A review of traffic simulation software[J].Research Letter in the Information and Mathematical Science，2009（13）：35-54.

[3]周溪召，許琰.車道寬度對信控交叉口通行能力及車輛延誤影響研究[J].華東交通大學學報，2016，33（6）：38-42.

[4]SUN D J，ZHANG L，CHEN F.Comparative study on simulation performances of CORSIM and VISSIM for urban street network [J].Simulation Modelling Practice and Theory，2013（37）：18-29.

[5]何兆成，佘錫偉，楊文臣，等.結合Q學習和模糊邏輯的單路口交通信號自學習控制方法[J].計算機應用研究，2011，28（1）：199-202.

[6]CHEU R L，JIN X，NG K C，et al.Calibration of FRESIM for Singapore expressway using genetic algorithm[J].Journal of Transportation Engineering，1998，124（6）：526-535.

[7]LEE D，XU Y，CHANDRASEKHAR P.Parameter calibration for PARAMICS using genetic algorithm[C]//The 80th Transportation Research Board Annual Meeting，Washington D.C.，2001.

[8]PRAK B，QI H.Development and evaluation of simulation model calibration procedure[C]//The 84th Transportation Research Board Annual Meeting，Washington D.C，2005.

[9]李志明，閆小勇.基于遺傳算法的交通仿真模型參數校正方法研究[J].交通標準化，2006（4）：21-23.

[10]孫劍，楊曉光，劉好德.微觀交通仿真系統參數校正研究[J].系統仿真學報，2007，19（1）：48-50.

[11]周素霞，陳森發.基于遺傳算法的VISSIM參數校正及其交通流應用[J].交通科技，2009（2）：89-91.

[12]唐少虎，劉小明.基于IAGSO算法的VISSIM模型校正研究與實現[J].交通運輸系統工程與信息，2014，14（5）：74-80.

[13]PTV.VISSIM 5.4 User Manual[Z].PTV Planung Transport Verkehr AG，2012.

[14]楊文臣，張輪，饒倩，等.基于黃金分割點遺傳算法的交通信號多目標優化[J].交通運輸系統工程與信息，2013，13（5）：48-55.

[15]SUN Y X，VAN B J，WANG Z H.A new golden ratio local search based particle swarm optimization[C]//The 2012 International Conference on Systems and Informatics，2012：754-757.

[16]何兆成，楊文臣，梁詩，等.城市單交叉路口交通信號實時優化控制與仿真[J].計算機工程與應用，2010，46（33）：239-243.

Parameter Calibration of VISSIM Simulation Model Based on Golden-Ratio Genetic Algorithm

Yang Wenchen1，2，Zhang Lun2，Wang Zheng2，Hu Chengyu1
（1.National Engineering Laboratory for Surface Transportation Weather Impacts Prevention,Broadvision Engineering Consultants，Kunming 650031，China；2.Key Laboratory of Road and Traffic Engineering of the Ministry of Education,Tongji University，Shanghai 201804，China）

The accuracy of microscopic traffic simulation model has direct influence on the reality of the simulation scene.By using the golden-ratio genetic algorithm，this paper presented the parameter calibration of VISSIM simulation model.Firstly，the standard process of microscopic traffic simulation and the mechanism of parameter calibration of VISSIM simulation model were discussed in details.Then，based on the throughput index，the objective function and discretization of GA individual parameter were designed，and the calibration algorithm of VISSIM simulation model was developed by golden-ratio genetic algorithm.Finally，taking a typical signalized intersection as the example，it analyzed the characteristics of calibrated traffic flow model and explored the effectiveness of the proposed algorithm by comparing with the observed traffic data in the field.Results show that drivers in China have aggressive driving habits，and the proposed algorithm significantly improve the accuracy of simulation model，while the parameter calibration effectiveness is related to the traffic intensity at the intersection.

microscopic traffic simulation；parameter calibration；golden-ratio genetic algorithm；parameter discretization；VISSIM

1005-0523（2017）03-0095-08

TP391.9；U491.51

A

（責任編輯 姜紅貴）

2017－01－09

云南省交通廳科技計劃（云交科2014(A)23）；國家863計劃課題（2012AA112307）

楊文臣（1985—），男，博士，主要研究方向為人工智能、智能交通控制系統、交通安全。

張輪（1971—），男，教授，博士，博士生導師，主要研究方向為智能交通運輸系統。