充電模態下電動汽車動力電池模型辨識

劉偉龍 王麗芳 廖承林 王立業

(1.中國科學院電力電子與電力傳動重點實驗室(電工研究所) 北京 100190 2.中國科學院大學 北京 100049)

?

充電模態下電動汽車動力電池模型辨識

劉偉龍1,2王麗芳1廖承林1王立業1

(1.中國科學院電力電子與電力傳動重點實驗室(電工研究所) 北京 100190 2.中國科學院大學 北京 100049)

電池模型及參數辨識是電動汽車動力電池進行充、放電優化控制的基礎，同時模型參數受充、放電工況的影響。為對充電模態下的電動汽車動力電池進行建模與參數辨識，對動力電池建模方法、模型參數辨識算法展開研究，建立基于電極阻抗譜理論的可變階次電池等效電路模型，提出基于遺忘因子擴展遞推最小二乘算法(FFRELS)的模型參數辨識算法，構建基于貝葉斯信息準則(BIC)的電池模型最優階次選擇算法，創建基于晶格氣體模型(LGM)的電池開路電壓模型，對電池模型參數辨識算法進行修正，實現了充電模態下的電池模型參數辨識與最優階次選擇。仿真結果證明了該方法的有效性。

電池模型 參數辨識 遺忘因子 貝葉斯信息準則 晶格氣體模型

0 引言

電動汽車使用電能代替燃油，是解決能源危機與環境問題的重要手段。目前，電動汽車作為汽車產業的發展方向已經成為普遍共識。動力電池是電動汽車的主要能量來源，決定著電動汽車的續航里程、動力性能以及使用經濟性等。由于鋰離子電池具有能量密度高、工作電壓窗口寬、循環壽命長和沒有記憶效應的優點，已成為電動汽車動力電池的首要選擇。電動汽車在使用過程中，動力電池有充、放電兩種工作模態。因為相較于傳統汽車，電動汽車的能量補給速度有很大劣勢，所以動力電池充電成為制約電動汽車推廣的關鍵因素[1]。而電池模型及參數辨識是動力電池進行充電優化控制的基礎。因此，建立能夠通過動力電池的輸入(激勵電流)輸出(響應電壓)信息估算電池內部狀態的電池模型，并研究充電模態下的動力電池模型參數實時辨識方法具有重要意義。

目前，動力電池模型的研究主要分為三類：電化學機理模型[2,3]、經驗模型[4-6]和等效電路模型[7,8]。其中，電化學機理模型通過電化學反應第一性原理，以偏微分方程描述電化學動力學過程，含有大量先驗電化學參數，計算復雜，不具備通用性。經驗模型是基于實驗數據通過輸入輸出量的非線性關系來表征其外部特性，該模型依賴于實驗數據，很難滿足預測精度要求。等效電路模型是將電池等效為集總參數電路，具有便于分析應用、通用性好的優點，取得了廣泛應用。

在電池模型參數辨識方面，須基于一定的電池測試方法才能對電池模型參數進行辨識，現有的電池測試方法主要有兩種：基于電動汽車運行工況得到的電池電流-時間曲線[9]；基于統計學分析設計的電池電流-時間曲線[10]。當電池模型參數辨識方法應用于充電模態下的動力電池參數辨識時，卻有其局限性。常規充電模態主要有恒壓充電、恒流充電和恒流-恒壓充電。在常規充電模態下，電池的動態特性并不能得到充分激發，因此，電池模型參數辨識方法應用于充電模態時，并不能得到足夠精確的模型參數，需進一步對此結論進行驗證。綜上，本文從充電模態下電池模型參數辨識的角度，對電池模型建立與模型參數辨識方法展開研究。

1 鋰離子動力電池模型

建立電池模型是進行電池狀態觀測與優化控制的基礎[11-13]。電池在充、放電的過程中，內部狀態主要有歐姆極化、濃差極化和電化學極化[14]。典型的電池電路模型有Rint模型、Thevenin模型和DP模型等[15,16]。但這些模型的參數與電池內部狀態并不具備一一對應的關系。基于電極阻抗譜理論[17]，建立的電池電路模型如圖 1所示。圖1中：Uoc為電池開路電壓；Rs為電池等效內阻，與電池歐姆極化對應；Cdl為雙電層電容，與電池濃差極化對應；ZF為電化學阻抗，與電池電化學極化對應；Rt為電荷轉移電阻；n為模型階次，n=0,1,2,…；nRC對應于電化學極化遲滯效應，RC數量越多，電池模型的精度越高，運算越復雜；Ut為電池端電壓；iL為電池電流，充電為正，放電為負。下面對電池模型進行離散化處理，以便于應用參數辨識算法對電池模型參數進行辨識。

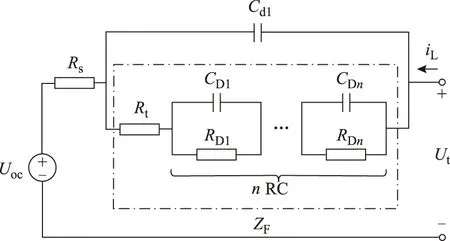
圖1 鋰離子動力電池電路模型結構Fig.1 Schematic of the lithium-ion power battery circuit model

首先，由基爾霍夫電壓定律得到動力電池模型輸出電壓與輸入電流的復頻域數學關系表達式為

(1)

式中

(2)

其次，利用雙線性變換法，將電池模型復頻域式(1)從s平面映射到Z域，映射公式為

(3)

式中，Δt為系統的采樣時間。將式(3)代入式(1)得電池模型Z域表達式為

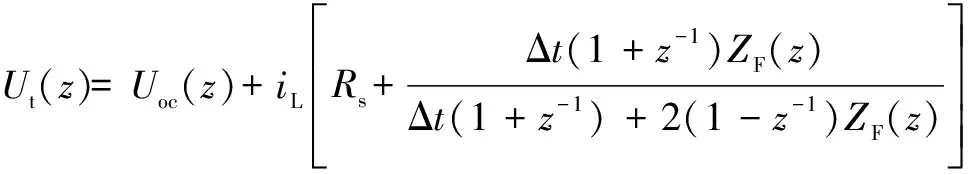
(4)

最后，因為動力電池開路電壓Uoc與荷電狀態(StateofCharge，SOC)、工作溫度T、老化狀態(State of Health，SOH)具有耦合關系，而通常情況下Δt非常小，所以在nΔt內假設SOC、T和SOH的變化均近似為0。因此，在nΔt內，電池開路電壓Uoc變化近似為0，即

Uoc,k≈Uoc,k-1≈…≈Uoc,k-n

(5)

式中，k為采樣時刻。對式(4)進行z逆變換，并將式(5)代入整理后，可得電池模型第k個采樣時刻輸出電壓的時間域離散表達式為

an+1Ut,k-n-1+an+2iL,k+an+3iL,k-1+…+a2n+3iL,k-n-1

(6)

式中，ai為電池模型參數構成的待辨識參數，i=1,2,…,2n+3。

2 電池模型參數辨識方法

鋰離子動力電池是一個參數時變的系統。本文鋰離子動力電池模型參數辨識方法采用遺忘因子擴展遞推最小二乘(ForgettingFactorRecursiveLeastSquare,FFRELS)算法，FFRELS結合遺忘因子遞推最小二乘算法和遞推擴展最小二乘(RecursiveExtendedLeastSquare,RELS)算法，繼承了FFRLS和RELS算法的優點，可以解決因采集數據的增多出現的“數據飽和”問題，并且可以將每一次預測值相對測量值的偏差作為下一時刻的輸入，進行迭代運算，提高了參數辨識的精度。

2.1FFRELS辨識算法

對于式(6)所示的電池輸出表達式，可將其改寫為矩陣相乘的形式，即

Ut,k=Φn,kθn,k

(7)

其中

Φn,k=[1,Ut,k-1,…,Ut,k-n-1,iL,k,…,iL,k-n-1]

(8)

θn,k=[a0,a1,…,a2n+3]T

(9)

(10)

式中，Φn,k為數據矩陣；θn,k為參數矩陣。

以yk表示電池電壓的測量值，則電池系統方程可表示為

yk=Φn,kθn,k+ek

(11)

式中，ek為電池系統的有色噪聲，其計算式為

ek=ξk+c1ξk-1+…+cncξk-nc

(12)

將ξk-i(i=1,…,nc)作為系統的輸入置入系統數據矩陣，則電池系統方程可改寫為

(13)

其中

(14)

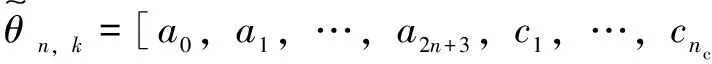
(15)

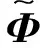
(16)

(17)

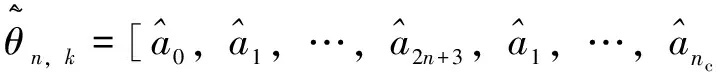
(18)

根據指數遺忘法，設定FFRELS的性能指標為

(19)

式中，λ為遺忘因子,0<λ≤1，本文取0.99；L為電池測試數據長度。使式(19)最小的電池系統參數矩陣為最優估計。該方法對測試數據施加了時變加權系數，最新的數據用1加權，而前面第n個采樣周期的數據則用λn加權。為實現電池模型參數在線實時辨識，須將上述算法轉換為遞推算法，推導過程參考遞推最小二乘算法[18]，得到FFRELS遞推公式為

(20)

2.2 電池模型階次選擇

基于以上模型參數辨識算法，進行模型參數辨識，還須確定電池的模型階次。電池模型階次越高，模型對電池系統的輸出預測精度就越高，但計算越復雜。因此，需要對電池模型階次進行優化選擇。

本文基于貝葉斯信息準則(BayesianInformationCriterions,BIC)選擇最優模型階次。BIC是考評綜合最優配置的指標，為模型估計精度和模型參數數量的加權函數，是對赤池信息準則(AkaikeInformationCriterion,AIC)[19]的改進，考慮采集數據長度的影響。基于本文的電池模型，簡化后的BIC為

(21)

式中，N為BIC采用的數據窗口寬度，N=10；p為電池模型參數數量，是模型階次的函數，p=2n+3。式(21)右邊第一項表示模型階次對計算復雜度的影響，lnN為懲罰系數；右邊第二項表示模型的預測精度。最小BIC值對應的模型階次為最優階次。

2.3 參數辨識算法與模型階次選擇實現

FFRELS算法的實現步驟為：

1)設置初始模型階次n為0。

3)采樣當前輸出數據yk和輸入數據iL,k。

6)數據更新迭代，時刻由k→k+1，返回步驟3，進行循環直至完成參數辨識計算。

7)BIC判定，根據式(21)計算BIC值，模型階次加1，返回步驟2，重新進行循環，再次計算BIC值，直至得到不同階次電池模型的BIC值，某一時刻最小BIC值對應的模型階次即為這一時刻模型的最優階次。

3 電池實驗測試方法

本文選用雙登50 A·h磷酸鐵鋰電池作為實驗對象，電池參數見表 1。電池模型參數辨識算法是利用電池測試方法激發的電池動態特性來辨識模型參數，所以對電池測試方法的要求是能有效激發電池所有的動態特性，或者是能有效激發電池使用工況下的所有動態特性。傳統的電池模型參數辨識實驗測試方法通常是在放電模態下對電池進行測試，并不適用于動力電池充電模態下的模型參數辨識。常規動力電池充電方法中的恒流-恒壓充電是目前應用最為廣泛的充電方法。因此，本文采用恒流-恒壓充電方法對實驗電池進行充電測試，測試曲線如圖 2所示。其中，恒流充電階段采用恒流10 A充電，恒壓充電階段采用3.65 V進行充電，當恒壓充電階段充電電流小于0.5 A時，充電結束。為驗證FFRELS算法的有效性和電池測試方法對電池模型參數辨識的影響，對電池進行了放電測試作為對比實驗。放電測試實驗采用由FUDS(federal urban driving schedule)工況對應的電池電流-時間曲線，如圖 2所示。

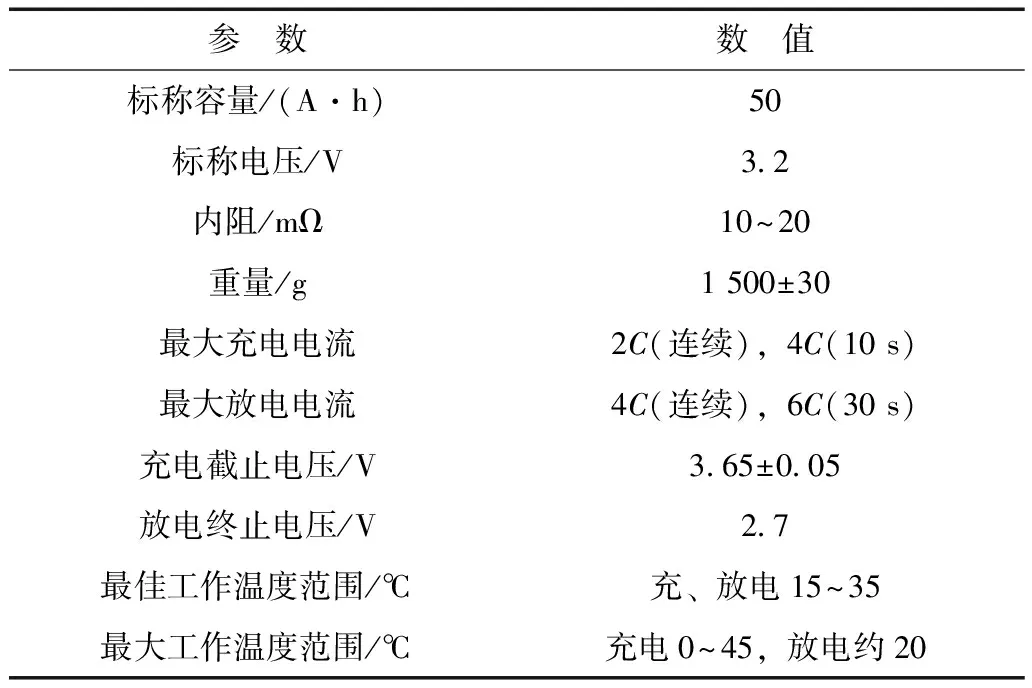
表1 磷酸鐵鋰動力電池技術規格

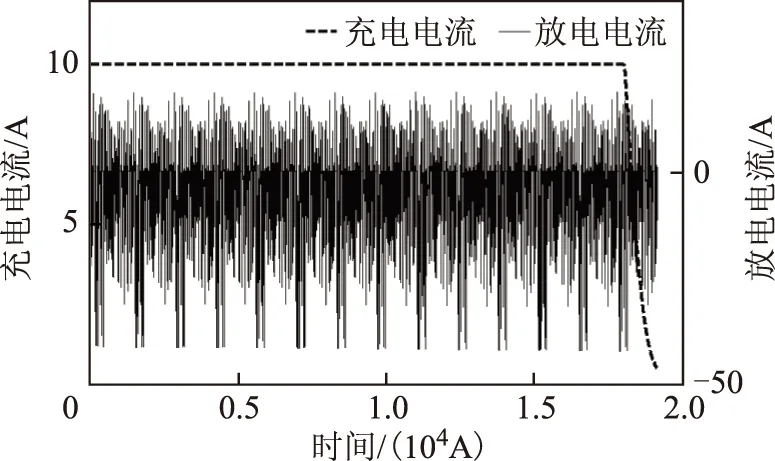
圖2 動力電池充、放電測試曲線Fig.2 Charging and discharging test curves of the power battery

4 參數辨識方法驗證與優化

基于上述鋰離子動力電池模型與電池實驗測試方法，對FFRELS進行驗證。驗證分為兩方面：FFRELS有效性驗證；測試工況對FFRELS的影響驗證。其中，FFRELS有效性驗證也包括兩方面：算法估計電池端電壓準確度驗證;算法辨識模型參數有效性驗證。對于算法估計電池端電壓準確度的驗證，通常采用實驗電池標稱電壓的1%作為判斷依據，即當最大辨識誤差小于32 mV時，認為估計電壓精度滿足要求。對于算法辨識模型參數有效性的驗證，電池模型參數中開路電壓Uoc可測量得到，因此本文將其作為參數辨識有效性的判斷依據。下面將基于電池0～5階模型對參數辨識方法進行驗證。

4.1 參數辨識方法的驗證

首先，基于動力電池放電測試數據，驗證FFRELS對電池端電壓估計的準確度和放電測試工況對FFRELS算法的影響。基于不同階次模型的FFRELS電池端電壓估計誤差如圖 3所示，算法收斂后的估計誤差始終小于11mV，小于電壓估計準確度評判標準32mV，參數辨識結果初始誤差較大，但算法能較快實現收斂。初始辨識誤差大的原因是電池模型參數初始設置值與真實值之間存在較大差異。由圖 3局部放大圖可以看出，不同階次模型的電壓估計誤差呈現規律近似的波動特性，對照圖 2中的放電工況，可以看出放電工況的劇烈變化影響參數辨識算法的電壓估計誤差。不同階次模型對應的BIC值如圖 4所示，不同階次模型的BIC值隨時間呈現一定的波動特性，由局部放大圖可以看出并不存在始終最優的模型階次。FFRELS對不同階次模型的電壓估計誤差分析見表 2，不同階次模型的電壓估計誤差平均值均小于1mV，而電壓估計誤差最大值均小于80mV，這是因為FFRELS尚未收斂導致。由分析可知，在放電模態下FFRELS收斂后對電池模型電壓估計準確度有效，放電工況影響FFRELS的電壓估計誤差，并且不同階次模型的BIC值隨放電工況呈現一定的波動特性，不存在始終最優的模型階次。

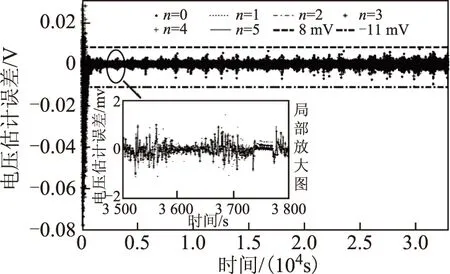
圖3 放電模態不同階次電池模型電壓估計誤差Fig.3 Voltage estimation deviations of different order battery models with discharging data

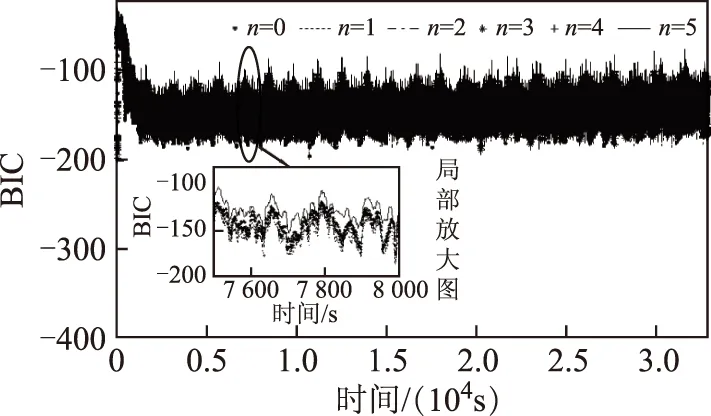
圖4 放電模態不同階次電池模型BIC值Fig.4 The BIC of different order battery models with discharging data

其次，基于動力電池充電測試數據，驗證FFRELS對電池端電壓估計的精準確度和充電測試工況對FFRELS的影響。不同階次模型對應的電池端電壓估計誤差如圖5所示，不同階次模型電池端電壓估計誤差始終小于10mV，小于電壓估計準確度評判標準32mV，FFRELS實現了快速收斂，但是FFRELS電壓估計誤差存在大量奇異值。由圖 5局部放大圖可以看出，不同階次模型的端電壓估計誤差呈現規律近似的波動特性，對比圖 3局部放大圖可知,平穩的充電測試工況帶來電池端電壓估計誤差的平穩波動特性，劇烈變化的放電測試工況導致電池端電壓估計誤差的劇烈波動。充電模態下不同階次模型對應的BIC值如圖 6所示，可以看出充電模態下不同階次模型的BIC值同樣存在波動特性，由局部放大圖可以看出，不存在始終最優的模型階次。不同階次模型的FFRELS電壓估計誤差分析見表 3，可知FFRELS對不同階次模型輸出電壓的平均估計誤差均小于0.05 mV，最大電壓估計誤差均小于10 mV。對比圖 3和圖 5可知，FFRELS在充電測試工況下可以更快地實現收斂。因此，FFRELS在電池充電模態下對電池端電壓估計的準確度有效，并且與放電模態相比擁有更高的估計精度，電池的充放電測試工況影響電池端電壓估計誤差，不同模型階次的BIC值隨充電工況呈現一定的波動特性，不存在始終最優的模型階次。

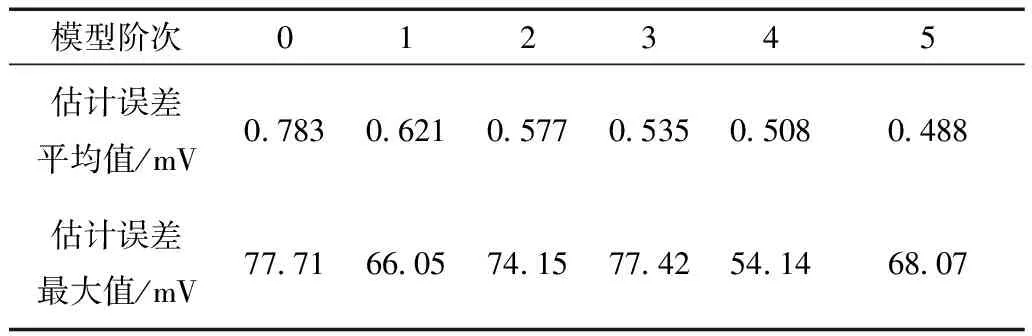
表2 放電模態下不同階次模型電壓估計誤差分析

圖5 充電模態不同階次電池模型電壓估計誤差Fig.5 Voltage estimation deviations of different order battery models with charging data

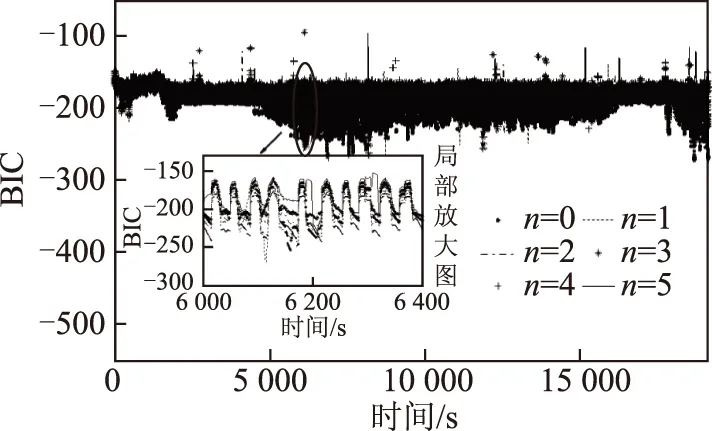
圖6 充電模態不同階次電池模型BIC值Fig.6 The BIC of different order battery models with charging data

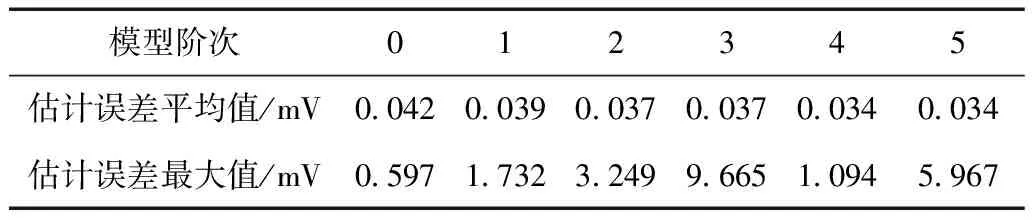
模型階次012345估計誤差平均值/mV0 0420 0390 0370 0370 0340 034估計誤差最大值/mV0 5971 7323 2499 6651 0945 967

最后，基于動力電池的放電和充電測試數據，驗證FFRELS辨識模型參數的有效性。對電池0～5階模型，采用FFRELS分別辨識電池充、放電模態下的開路電壓，結果如圖7所示。本文實驗用的動力電池的開路電壓范圍在2.7～3.5 V之間，并且由上文假設在采樣時間Δt內，SOC變化近似為0，根據電池開路電壓與SOC的對應關系可知，在某個測試點附近電池開路電壓應基本保持不變。但是由圖7a所示放電模態下開路電壓的估計值在大部分測試時間內遠小于2.7V，圖7b所示充電模態下開路電壓估計值存在大量-400～100V之間的奇異值，并且從圖7a、圖7b局部放大圖看，開路電壓估計值波動劇烈。因此，可知FFRELS對電池開路電壓辨識結果是不準確的。這是因為辨識的電池模型參數表示的是電池測試曲線所激發的電池動態特性，并不能反映電池的本征特性，所以不同測試工況將影響電池模型參數的準確辨識。同時，由于FFRELS在充電模態下對電池模型參數的辨識結果產生了奇異值，這也影響電池模型參數的求解，因此在充電模態下電池開路電壓的估計值也產生了大量奇異值。

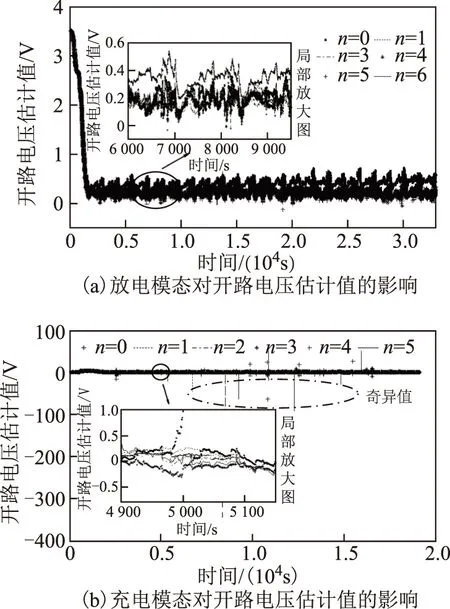
圖7 充、放電模態對動力電池開路電壓估計值的影響Fig.7 The influence of charging and discharging mode to the power battery′s open circuit voltage estimations

綜上分析，不論FFRELS在電池放電模態下還是充電模態下，都可以對電池端電壓進行有效地估計，但是電池測試工況會對FFRELS的電壓估計精度、算法收斂速度和電池模型參數估計造成影響。即基于測試數據辨識得到的電池模型，具有與測試電池相同的輸出特性，但電池模型參數卻并不能表征電池的內部狀態，此時的電池模型參數只與電池測試方法相關。因此，要辨識得到電池模型的準確參數，就必須對辨識算法進行優化改進。

4.2 參數辨識算法的優化

參數辨識算法的修正可以從兩個方面進行考慮：①設 計可以激發動力電池全部動態特性的電池測試方法；②從修正電池部分狀態參量估計值的角度對參數辨識算法進行改進，即對動力電池的開路電壓估計值進行實時修正，從而實現對電池其他狀態參量的精確估計。

對于前者，很難設計可以完全激發電池動態特性的測試曲線。同時，電池在充電模態下進行參數辨識，可供選擇的充電方法有限。因此，采用開路電壓修正的參數辨識算法是較為可行的方案。

電池的開路電壓通常采用多項式進行擬合，而此種方式擬合的結果并不理想。因此本文采用基于晶格氣體模型[20](LatticeGasModel，LGM)的鋰離子動力電池開路電壓模型來描述鋰離子動力電池開路電壓。對于晶體嵌入材料，因LGM考慮了離子電勢、嵌入離子熵值、離子相互作用對電勢的影響和嵌入電子電勢，在計算電池電動勢領域得到了成功的應用。LGM的表達式為

(22)

式中，U為電極電勢；E0為離子電勢；k為玻耳茲曼常數；T為熱力學溫度；xr為晶格中離子的占有率；Wxr為離子間相互作用對電勢的影響；Vel為嵌入電子電勢。

基于LGM的鋰離子動力電池開路電壓模型為

Uoc=a+bz+cz2+dz3+ez4+fz5+gz6+hz7+

(23)

式中，a、b、c、d、e、f、g、h、i、j、l、m、n、p、q為模型擬合參數；z為電池的SOC值，具體推導過程見附錄。電池開路電壓數據采用充、放電5A·h靜置2h取平均值的方法得到，并使用最小二乘法進行曲線擬合，擬合曲線如圖 8所示。需要說明的是，本文采用電池SOC的定義為電池可用于充、放電的容量與電池標稱容量之比。由于本文測試電池的充、放電容量大于標稱容量，所以此電池充滿電時SOC大于1。

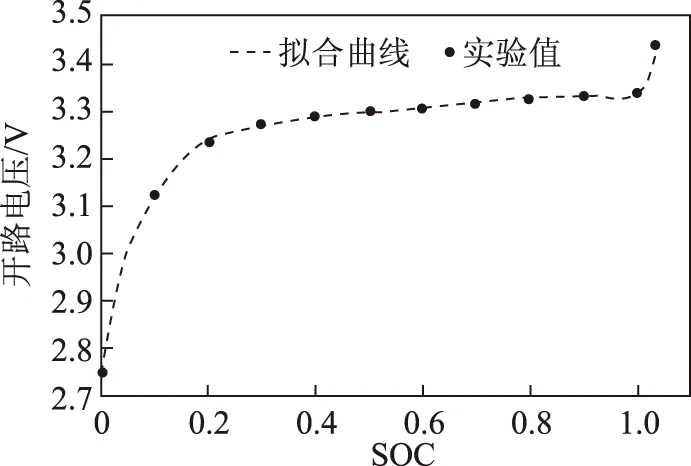
圖8 開路電壓擬合曲線Fig.8 The fitting curve of open circuit voltage

采用LGM開路電壓模型修正的FFRELS流程如圖 9所示，其中，Ek為電池的極化電壓，包括歐姆極化電壓、濃差極化電壓和電化學極化電壓，Ek=yk-Uoc,k。基于動力電池的充電測試數據，使用修正的FFRELS對動力電池0～5階模型進行參數辨識。不同模型階次對應的電池端電壓估計誤差如圖 10所示，不同階次模型輸出電壓最大估計誤差不超過0.4mV，相比算法修正前有明顯的改善，遠小于電壓估計精確度評判標準32mV，并且算法不存在電壓估計奇異值，可實現快速收斂。不同階次模型參數辨識算法估計值分析見表 4，不同階次模型輸出電壓的平均估計誤差均小于0.04mV，相比算法修正前電壓估計精度也有提高。

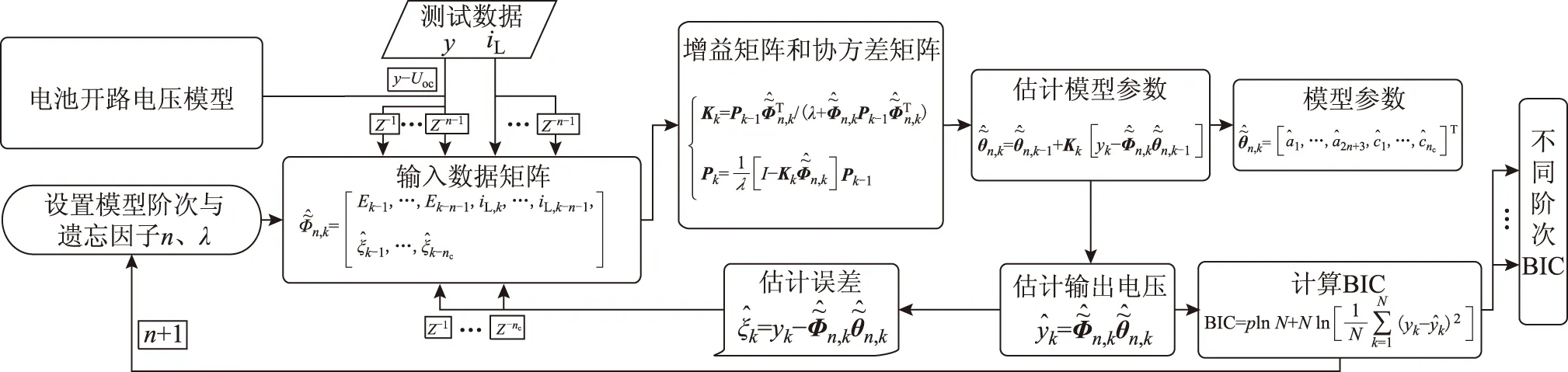
圖9 LGM開路電壓模型修正的FFRELS算法流程Fig.9 The amended FFRELS algorithm with the LGM open circuit voltage model

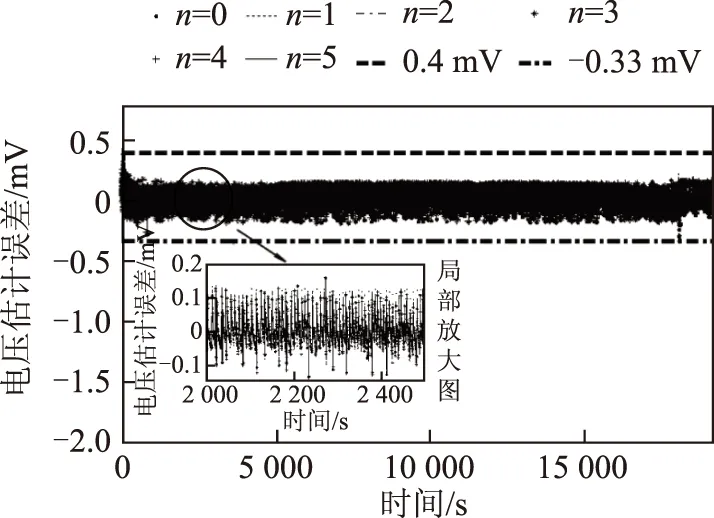
圖10 充電模態修正的模型電壓估計誤差Fig.10 Amended voltage estimated deviations of different order battery models with charging data

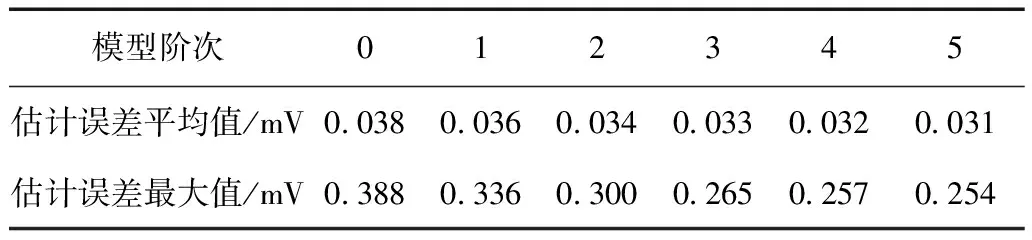
模型階次012345估計誤差平均值/mV0 0380 0360 0340 0330 0320 031估計誤差最大值/mV0 3880 3360 3000 2650 2570 254

修正的FFRELS對動力電池0～5階模型辨識的BIC值如圖 11所示，由圖可看出修正算法對不同階次

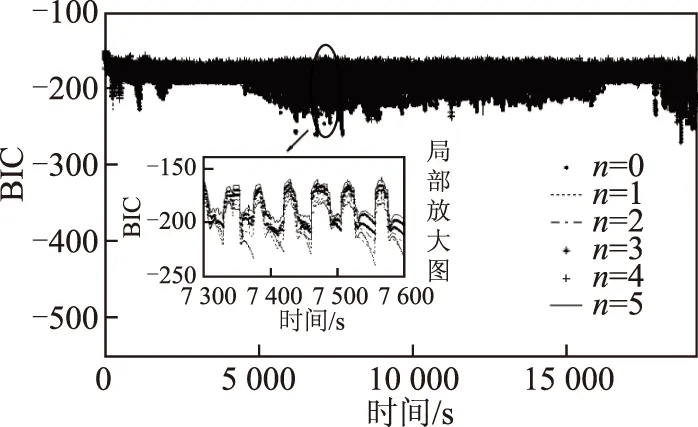
圖11 充電模態下修正的模型BIC值Fig.11 The amended BIC with charging data

模型的BIC值也存在一定的波動狀態，由局部放大圖可以看出不存在始終最優的模型階次。最小的BIC值對應的最優模型階次的時間與整個充電過程時間之比用餅狀圖 12表示，可以看出0和1階次作為電池模型最優階次的時間占比99%，為電池模型主要的最優階次，考慮到修正FFRELS對動力電池0～5階模型的電壓估計始終滿足精確度評判標準，可認為在本文測試充電模態下，電池模型的最優階次可通過BIC在0和1之間選取。

修正的FFRELS對電池開路電壓估計值及估計誤差如圖13所示，由于對FFRELS采用LGM開路電壓模型進行了修正，所以電池開路電壓估計誤差與電池端電壓估計誤差相等；并且電池測試方法不再對電池的開路電壓辨識造成影響，而是對電池模型極化參數產生作用，因此修正的FFRELS辨識得到的是與電池測試方法相關的電池極化參數，可以表征電池在特定測試方法下的內部極化狀態。同時，該修正的FFRELS也適用于電池放電模態下的模型參數辨識，限于本文篇幅，在此不進行討論。

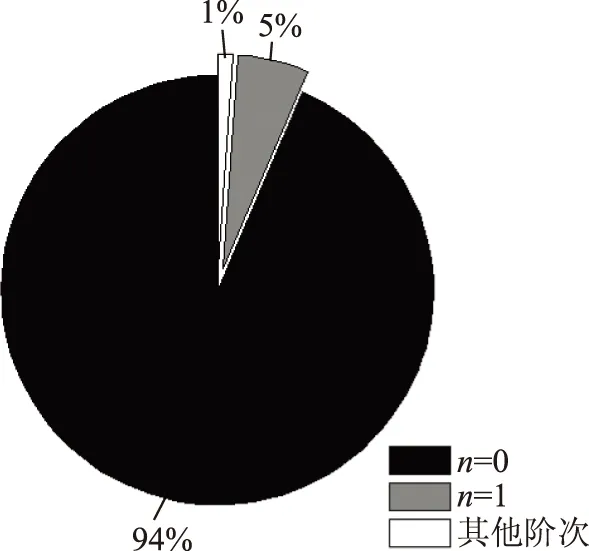
圖12 最優模型階次時間占比餅狀圖Fig.12 The pie chart of optimal battery model′s time ratio

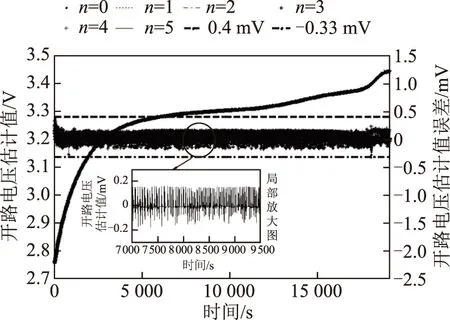
圖13 充電模態下修正的模型開路電壓估計值及誤差Fig.13 Amended open circuit voltage and estimated deviations with charging data

5 結論

本文圍繞充電模態下電動汽車動力電池模型辨識這一核心問題，提出基于FFRELS的參數辨識算法，建立基于電極電化學阻抗譜理論的電池電路模型，并進行模型參數辨識研究，采用BIC準則對電池模型階次進行優化選擇，并使用基于LGM的電池開路電壓模型對參數辨識算法FFRELS進行修正。

通過對模型參數辨識算法的驗證表明，FFRELS滿足動力電池模型輸出電壓精度的評判標準，并且不依賴于電池的工作模態與測試工況，但辨識得到的動力電池模型參數有效性與電池工作模態和測試工況相關。針對充電工況選擇有限的問題，采用基于LGM的電池開路電壓模型對FFRELS進行修正，修正的FFRELS可以避免測試工況對電池開路電壓參數辨識的影響，辨識得到的動力電池模型參數可以反映該測試工況下的電池極化特性，修正的FFRELS對電池端電壓及開路電壓的平均估計誤差小于0.04 mV，最大估計誤差小于0.4 mV，可以很好地滿足電動汽車的使用需求。

通過BIC計算表明，不同階次動力電池模型的BIC值呈現波動特性，不存在始終最優的模型階次。通過對不同階次模型BIC值分析得到0和1為本文恒流-恒壓充電模態下動力電池模型的主要最優階次，在滿足電壓估計精度評判標準的前提下，通過BIC可在0和1之間選擇動力電池模型最優階次。由于本文提出的電池模型及參數辨識算法并不依賴于本文使用的鋰離子電池，因此具有較好的普遍適用性。

附錄 鋰離子動力電池開路電壓模型

鋰離子動力電池由正、負兩電極組成，因此開路電壓可表示為

Uoc=U+-U-

(A1)

式中，U+為正極電勢；U-為負極電勢。

在鋰離子動力電池充、放電循環過程中，為保護電極材料晶體結構，須防止電極材料中鋰離子過度脫嵌[21]，即電極材料中有部分鋰離子并不參與充、放電。因此正、負極材料晶格中鋰離子的占有率可以表示為

(A2)

式中，C+、C-分別為正、負電極內鋰離子數；Cm+、Cm-分別為正、負電極內鋰離子最大數；Czm+、Czm-分別為正、負電極內參與一次充電或放電的鋰離子最大數，Czm+=Czm-=Czm；Cz+、Cz-分別為當前正、負電極材料內可用于充電或放電的鋰離子數，Cz++Cz-=Czm；C0+、C0-分別為正、負電極不用于充電或放電的鋰離子數，且均大于零。電池的標稱容量對應的鋰離子數用C表示，正、負極材料晶格中鋰離子的占有率可改寫為

(A3)

式中，Cz-/C為電池的荷電狀態，即SOC；Czm/C為電池真實容量與標稱容量之比，用1+r′替代；C0+/C表示電池正極不參與充放電的容量與標稱容量之比，用p′代替；C0-/C為電池負極不參與充放電的容量與標稱容量之比，用n代替。則正、負極材料晶格中鋰離子的占有率可改寫為

(A4)

將式(A4)代入式(22)可得

(A5)

將式(A5)代入式(A1)得

Uoc=E0+-E0--(Wxr+-Wxr+)+Vel+-Vel-+

(A6)

式中，E0+-E0--(Wxr+-Wxr+)+Vel+-Vel-與電池的荷電狀態z相關，本文采用多項式擬合的方式得到，因此式(A6)可改寫為

Uoc=a+bSOC+cSOC2+dSOC3+eSOC4+fSOC5+gSOC6+

(A7)

LGM模型描述的是理想晶格材料的電勢特性，并在xr等于0或1時模型失效。根據上文討論，因C0+、C0-均大于零，所以由式(A2)可知xr>0。為提高模型適用性并解決xr=1模型失效的問題，采用擬合參數j、l代替式(A7)中的參數kT和增加擬合參數m的方法，則

Uoc=a+bSOC+cSOC2+dSOC3+eSOC4+fSOC5+gSOC6+

(A8)

令r′+p′=p、r′+m=q，滿足m>0，且1+q大于電池充滿電時SOC，可得鋰離子動力電池開路電壓模型為

Uoc=a+bSOC+cSOC2+dSOC3+eSOC4+fSOC5+gSOC6+

(A9)

[1] 黨杰, 湯奕, 寧佳, 等. 基于用戶意愿和出行規律的電動汽車充電負荷分配策略[J]. 電力系統保護與控制, 2015, 43(16): 8-15.DangJie,TangYi,NingJia,etal.Astrategyfordistributionofelectricvehicleschargingloadbasedonuserintentionandtriprule[J].PowerSystemProtectionandControl, 2015, 43(16): 8-15.

[2]SmithKA,RahnCD,WangCY.ControlorientedIDelectrochemicalmodeloflithium-ionbattery[J].EnergyConversionandManagement, 2007, 48(9): 2565-2578.

[3]SmithKA,RahnCD,WangCY.Model-basedelectrochemicalestimationandconstraintmanagementforpulseoperationoflithium-ionbatteries[J].IEEETransactionsonControlSystemsTechnology, 2010, 18(3): 654-663.

[4]ShenWX,ChanCC,LoEWC,etal.Anewbatteryavailablecapacityindicatorforelectricvehiclesusingneuralnetwork[J].EnergyConversionandManagement, 2002, 43(6): 817-826.

[5]ChauKT,WuKC,ChanCC.Anewbatterycapacityindicatorforlithium-ionbatterypoweredelectricvehiclesusingadaptiveneuro-fuzzyinferencesystem[J].EnergyConversionandManagement, 2004, 45(11-12): 1681-1692.

[6] 孫丙香, 高科, 姜久春, 等. 基于ANFIS和減法聚類的動力電池放電峰值功率預測[J]. 電工技術學報, 2015, 30(4): 272-280.SunBingxiang,GaoKe,JiangJiuchun,etal.ResearchondischargepeakpowerpredictionofbatterybasedonANFISandsubtractionclustering[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(4): 272-280.

[7]WaagW,FleischerC,SauerDU.On-lineestimationoflithium-ionbatteryimpedanceparametersusinganovelvaried-parametersapproach[J].JournalofPowerSources, 2013, 237(3): 260-269.

[8]WaagW,SauerDU.Adaptiveestimationoftheelectromotiveforceofthelithium-ionbatteryaftercurrentinterruptionforanaccuratestate-of-chargeandcapacitydetermination[J].AppliedEnergy, 2013, 111(4): 416-427.

[9]HeHongwen,XiongRui,GuoHongqiang.Onlineestimationofmodelparametersandstate-of-chargeofLiFePO4batteriesinelectricvehicles[J].AppliedEnergy, 2012, 89(1): 413-420.

[10]李勇, 王麗芳, 廖承林, 等. 基于子空間技術的電動汽車電池模型辨識研究[J]. 電工電能新技術, 2015, 34(1): 1-6.LiYong,WangLifang,LiaoChenglin,etal.Researchonsubspace-basedidentificationofbatterymodelforelectricvehicles[J].AdvancedTechnologyofElectricalEngineeringandEnergy, 2015, 34(1): 1-6.

[11]程澤, 董夢男, 楊添剴, 等. 基于自適應混沌粒子群算法的光伏電池模型參數辨識[J]. 電工技術學報, 2014, 29(9): 245-252.ChengZe,DongMengnan,YangTiankai,etal.Extractionofsolarcellmodelparametersbasedonself-adaptivechaosparticleswarmoptimizationalgorithm[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(9): 245-252.

[12]馮飛, 宋凱, 逯仁貴, 等. 磷酸鐵鋰電池組均衡控制策略及荷電狀態估計算法[J]. 電工技術學報, 2015, 30(1): 22-29.FengFei,SongKai,LuRengui,etal.EqualizationcontrolstrategyandSOCestimationforLiFePO4batterypack[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(1): 22-29.

[13]馮飛, 逯仁貴, 朱春波. 一種鋰離子電池低溫SOC估計算法[J]. 電工技術學報, 2014, 29(7): 53-58.FengFei,LuRengui,ZhuChunbo.StateofchargeestimationofLi-ionbatteryatlowtemperature[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(7): 53-58.

[14]MitsudaK,TakemuraD.Polarizationstudyofalithium-ionbatterywithanextrapositiveelectrodeusingeightreferenceelectrodes[J].Electrochemistry, 2008, 76(12): 880-885.

[15]HeHongwen,XiongRui,GuoHongqiang,etal.Comparisonstudyonthebatterymodelsusedfortheenergymanagementofbatteriesinelectricvehicles[J].EnergyConversionandManagement, 2012, 64(4): 113-121.

[16]劉艷莉, 戴勝, 程澤, 等. 基于有限差分擴展卡爾曼濾波的鋰離子電池SOC估計[J]. 電工技術學報, 2014, 29(1): 221-228.LiuYanli,DaiSheng,ChengZe,etal.Estimationofstateofchargeoflithium-ionbatterybasedonfinitedifferenceextendedkalmanfilter[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(1): 221-228.

[17]HuetF.Areviewofimpedancemeasurementsfordeterminationofthestate-of-chargeorstate-of-healthofsecondarybatteries[J].JournalofPowerSources, 1998, 70(1): 59-69.

[18]龐中華, 崔紅. 系統辨識與自適應控制MATLAB仿真[M]. 北京: 北京航空航天大學出版社, 2013.

[19]商云龍, 張奇, 崔納新, 等. 基于AIC準則的鋰離子電池變階RC等效電路模型研究[J]. 電工技術學報, 2015, 30(17): 55-62.ShangYunlong,ZhangQi,CuiNaxin,etal.Researchonvariable-orderRCequivalentcircuitmodelforlithium-ionbatterybasedontheAICcriterion[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(17): 55-62.

[20]KalikmanovVI,KoudriachovaMV,deLeeuwSW.Lattice-gasmodelforintercalationcompounds[J].SolidStateIonics, 2000, 136(11): 1373-1378.

[21]IslamMS,FisherCAJ.Lithiumandsodiumbatterycathodematerials:computationalinsightsintovoltage,diffusionandnanostructuralproperties[J].ChemicalSocietyReviews, 2014, 43(1): 185-204.

(編輯 張洪霞)

Parameters Identification Method of Battery Model for Electric Vehicles under the Charging Mode

LiuWeilong1,2WangLifang1LiaoChenglin1WangLiye1

(1.Key Laboratory of Power Electronics and Electric Drives Institute of Electrical Engineering Chinese Academy of Science Beijing 100190 China 2. University of Chinese Academy of Sciences Beijing 100049 China)

The battery model and parameters identification are the base of the charge and discharge optimal control of electric vehicle traction batteries. And the parameters of the battery model are affected by the working condition of the traction battery. In order to model the traction battery and identify the model parameters, modeling algorithm of traction battery and parameters identification method were studied in this paper. A variable order equivalent circuit model was established, which is based on the electrode impedance spectrum theory. A parameter identification algorithm was proposed, which is based on the forgetting factor recursive extended least square (FFRELS). A selection algorithm for the optimal order of the battery model was built, which is based on the Bayesian information criterions (BIC). A battery open circuit voltage model that was used for calibration of the proposed parameter identification algorithm was created, which is based on the lattice gas model (LGM). In the end, the battery model parameters identification algorithm and the optimal order selection under the charging mode was achieved. Validation results show that the proposed modeling and parameters identification algorithm is efficient.

Battery model, parameters identification, forgetting factor, Bayesian information criterions, lattice gas model

國家重點研發計劃項目(2016YFB0101801,2016YFB0101800)和國家電網公司科技項目“電動汽車基礎設施運行安全與互聯網互通技術”資助。

2016-03-05 改稿日期2017-01-04

TM912.8

劉偉龍 男，1988年生，博士研究生，研究方向為電動汽車電池管理技術。

E-mail：liuweilong@mail.iee.ac.cn(通信作者)

王麗芳 女，1971年生，博士，研究員，研究方向為電動汽車電池管理技術和電動汽車無線充電技術等。

E-mail：wlf@mail.iee.ac.cn