矩陣理論在AES中的應用

王志俊 姜詠梅

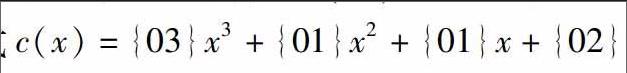
【摘要】矩陣是現(xiàn)代數(shù)學中最基本的概念之一.本文從矩陣運算的角度對高級加密標準中的字節(jié)代替變換和列混合變換給予解釋，說明了字節(jié)代替變換是狀態(tài)數(shù)組字節(jié)上的仿射變換，列混合變換是狀態(tài)數(shù)組列上的線性變換.

【關鍵詞】矩陣；高級加密標準；仿射變換；線性變換

2001年美國國家標準技術研究所（NIST）正式公布了高級加密標準（AES），并于2002年5月正式生效.AES被認為是沒有明顯缺點和安全漏洞的，能夠抵抗目前已知各種方法攻擊的、安全性能良好的密碼體制.AES是一種分組密碼，分組長度為128 bits，其加密和解密中的每個中間狀態(tài)也是128 bits.

設s是一個中間狀態(tài)，將s按從左到右的順序分為16個字節(jié)，然后，將這16個字節(jié)排成一個稱為狀態(tài)數(shù)組的4階方陣

一、字節(jié)代替變換

字節(jié)代替變換是將狀態(tài)數(shù)組中的每個字節(jié)通過S盒非線性地變換為另一個字節(jié).在教學過程中如果只簡單地通過S盒查表得到字節(jié)代替變換的輸出，會使部分學生產生一些困惑：這個S盒是如何得到的？為什么會有這樣的輸出？有了狀態(tài)數(shù)組矩陣，S盒產生輸出的過程就可以用矩陣的加法和乘法運算來代替：設a0a1a2a3a4a5a6a7是字節(jié)替代變換前狀態(tài)數(shù)組中（i，j）位置的一個字節(jié)，并將其看成是有限域GF（28）中的元素，先求出其乘法逆元，不妨假設為b0b1b2b3b4b5b6b7，則在字節(jié)替代變換后狀態(tài)數(shù)組中（i，j）位置的結果是通過下面的仿射變換得到的.

這樣的解釋既能夠讓學生聽懂，揭開S盒的神秘面紗，又可以讓學生學習到一個新的數(shù)學概念——仿射變換.

二、列混合變換

列混合變換是對狀態(tài)數(shù)組逐列進行變換，它將狀態(tài)數(shù)組中的每一列看作GF（28）上的一個多項式，然后，與多項式 做模x4+1乘法.客觀地說，要從這個角度講清列混合變換是有一定難度的，比如，為什么要與多項式c（x）做乘法，為什么模多項式是x4+1，等等，這需要具有有限域上多項式環(huán)、商環(huán)等抽象代數(shù)的基礎.基于這個原因，上面對列混合變換的處理顯得比較抽象，由于學習本課程的學生已經具備線性代數(shù)的基礎，我們可以用簡單的矩陣乘法來代替：任意取列混合變換前狀態(tài)數(shù)組的一列，比如，第j列，則列混合變換后狀態(tài)數(shù)組的第j列可以通過下面的矩陣乘法來表示

用上面矩陣乘向量（也可以理解為線性變換）來解釋列混合變換比較直觀，學生容易接受.當然，這樣處理也會產生一個問題：上面兩種處理列混合變換的方法是否等價？具體來講，給定狀態(tài)數(shù)組的一列，用上面兩種方法得到的結果是否相同？對此問題我們可以通過下面的計算給出簡單的證明.

將所得多項式的系數(shù)寫成列向量的形式就會發(fā)現(xiàn)它恰好可以用上面矩陣的乘法來表示.

三、結束語

現(xiàn)代密碼學與代數(shù)學（包括線性代數(shù)和抽象代數(shù)）之間有著緊密的聯(lián)系，許多密碼體制（比如，EIGamal公鑰密碼體制）的安全性都是基于代數(shù)學中的一些問題的難解性.所以，要在現(xiàn)代密碼學有深入的研究，離不開堅實的代數(shù)學知識.

【參考文獻】

[1]林東岱，曹天杰.應用密碼學[M].北京：科學出版社，2009：73-82.

[2]陳魯生，沈世鎰.現(xiàn)代密碼學[M].北京：科學出版社，2008：58-72.

[3]江龍，程林鳳，胡建華，魏琦瑛.線性代數(shù)[M].北京：高等教育出版社，2012：21-33.

[4]付麗，丁慧.代數(shù)在密碼學中的應用[J].通化師范學院學報，2014（35）：29-31.