智慧的教師需要“知錯而后教”

施凌燕

【摘要】學生錯誤的回答通常不是粗心所致，也不是教師沒有教過這方面的知識，而是對題目背后的概念理解不到位，或被題中非本質屬性的數據干擾，導致在解題時出現認知偏差.從一定程度上反映了學生的認知結構不完整，對知識的類比遷移能力較弱，所以，探求學生錯誤背后的原因，顯得非常重要.

【關鍵詞】錯誤；遷移

皮亞杰說過：“錯誤是有意義的學習所必不可少的.”錯誤是正確的先導，錯誤是學習的必然經歷.用皮亞杰的話來說，學習時犯錯誤是應該的，引發了學生的認知沖突或不平衡，引起認知圖式的順應或實現新的同化.我常反思：為什么有的知識教師利用最佳時間進行了反復的強化，學生再次碰到時仍出錯？筆者認為很大程度上是我們忽視了學生的學習實際，忽視了“錯誤”的價值及開發.

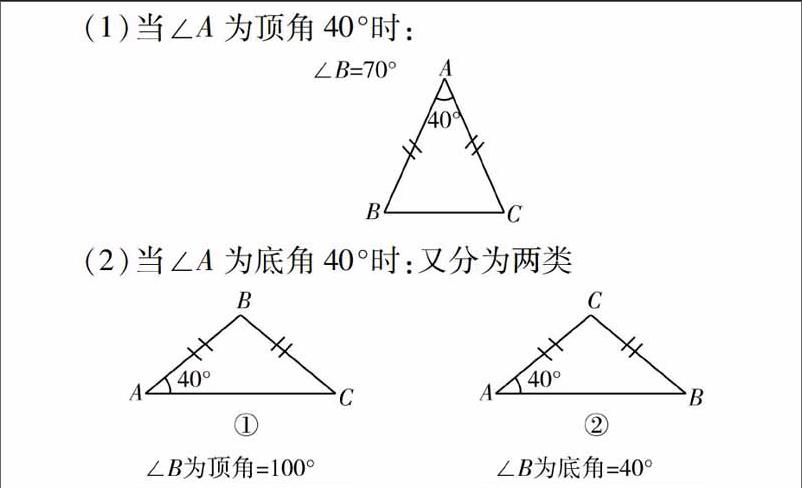
等腰三角形這一章分類討論的題目很多，如一個常見題：在等腰△ABC中，∠A=40°，求∠B的度數.學生往往只寫出一個或兩個答案，而正確答案有三個，我們會告訴學生等腰三角形的分類問題一般按頂點分三類才會不重不漏：∠A為頂角；∠B為頂角；∠C為頂角.可是學生下次再做同樣的題還是會漏寫答案，問題到底出在哪呢？是我們講解得不夠清晰透徹嗎？不是，我們若不能蹲下來去了解學生的需要、了解學生錯誤的原因，又何談有效教學呢？筆者采訪了幾位錯誤的學生，讓他們講一下自己的思路，原來學生大多數是這樣想的：當∠A為頂角40°時，∠B為底角=70°；當∠A為底角40°時，∠B為頂角=100°.也就是在第二類中學生定式地認為∠B為頂角，這就是病根，只有治好了這里，才能把學生治愈.按照學生的思路數形結合與學生共同探討得出：

教材中的習題是經過精挑細選的，具有一定的代表性，內隱著相關概念的本質屬性.作業中的“差錯”是一個信號，暴露出學生真實的思維過程，不同的錯誤反映了學生不同的思維誤區.學生只有知道自己錯在哪了，才不會犯同樣的錯誤，我決定抓住這個契機讓學生知道自己錯誤的真正原因，按照自己愿意接受的方式去理解，通過觀察圖形，會發現這與按頂點分成三類是相通的，比較之下還不會少情況，至于學生選擇哪種由他們自己去決定，不要強求，只要學生掌握了本質，又何必在乎形式呢！適合自己的方法就是最好的方法.最后，再總結出此類分類討論問題的一般思路，便于今后學習的遷移.

“錯題”讓課堂充滿生機和活力，教師應及時捕捉學生的錯題并因勢利導，讓學生在自我構建中掌握知識，避免在以后的學習中重蹈覆轍.教師與學生是需要互相學習的，教師的智慧是從學生中來再到學生中去.學生的智慧是需要教師去激發和挖掘的，他們能夠一通百通，這才是一名智慧的教師對于學生思維的真正引領.

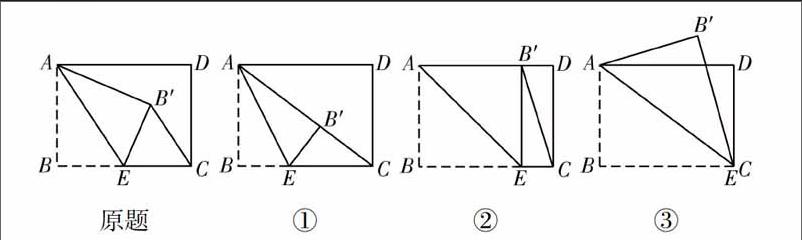
后續應用：如圖，在長方形ABCD中，AB=3，BC=4，點E是BC邊上一點，連接AE，把∠B沿AE折疊，使點B落在點B′處，當△CEB′為直角三角形時，BE的長為.

等腰三角形與直角三角形都是特殊三角形，由等腰三角形的分類討論思路遷移到直角三角形上來，學生自然會聯想到△CEB′的三個頂點在運動的過程中都可能成為直角頂點，所以按直角頂點分為三類，這是學生在自己的錯誤中吸取的教訓，更體現了數學教與學的精華之所在——融會貫通.

① 點B為直角頂點時；② 點E為直角頂點時；③ 點C為直角頂點時.

一個智慧的教師應該充分利用錯題，幫助學生分析錯因、走出思維的誤區，加深對數學知識與方法本質的理解，精講一個題，推廣一大類，為實現遷移提供最有力的保障.

學生學習數學的過程應該是一個不斷出錯、反復糾錯的過程.當學生出現錯誤時，不能簡單地歸結為“粗心”，大多數時候是由學生感知、注意、思維、記憶、情感等因素造成的，關鍵是找到學生在理解方面所存在的問題.學生需要經歷一些認知沖突，順化自己的知識結構，并把新的知識同化到修正過的知識結構中.要讓學生明白產生錯誤并不意味著失敗，它是學習過程中一個重要的必不可少的部分.對一個智慧的教師而言，“差錯”是一個信號，很好地暴露了學生真實的思維過程，是課堂教學中寶貴的教學資源.

【參考文獻】

[1]歐陽明.教師教育智慧的修煉[M].北京：北京師范大學出版社，2011.

[2]謝華勇.新課程標準下數學課堂教學理念的轉變[J].紹興文理學院學報（教育版），2006（11）：107-109.