構(gòu)造輔助圓解題

文 /沈岳夫

構(gòu)造輔助圓解題

文 /沈岳夫

責(zé)任編輯：王二喜

在解幾何與代數(shù)的綜合題時，有時遇到一些用常規(guī)方法較難解決的問題. 這時，我們可以構(gòu)造輔助圓來使問題轉(zhuǎn)化，從而簡捷地解決問題.

例 1 （2015年威海卷）如圖1，已知AB=AC=AD，蟻CBD=2∠BDC，蟻BAC=44°，則∠CAD的度數(shù)為（ ）

A.68°. B.88°. C.90°. D.112°.

解：如圖1，∵AB=AC=AD，

∴ 點B、C、D在以點A為圓心，以AB為半徑的圓上，

∵∠CBD=2∠BDC，蟻BAC=2∠BDC，蟻CAD=2∠CBD，∴∠CBD=∠BAC，

∴∠CAD=2∠BAC，而蟻BAC=44°，

∴∠CAD=88°. 選B．

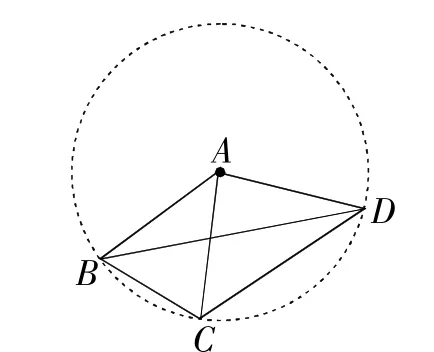
圖1

點評：該題主要考查圓周角定理及其推論的應(yīng)用.作輔助圓，將分散的條件集中，便于解題.

例 2 在△ABC中，蟻ABC=45°，tan∠ACB=．如圖2，把△ABC的一邊BC放置在x軸上，OB=14，OC=，AC與y軸交于點E．

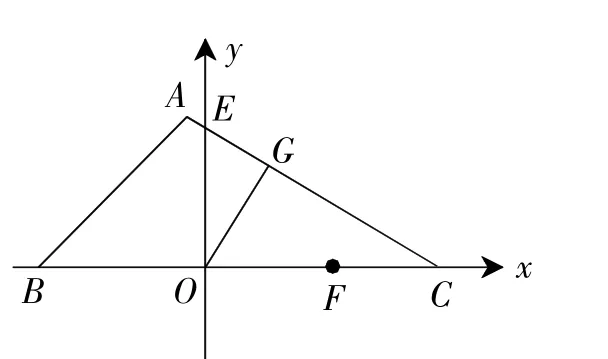
圖2

（1）求AC所在直線的解析式；

（3）已知點F（10，0），在△ABC的邊上取兩點P，Q，是否存在以O(shè)，P，Q為頂點的三角形與OFP全等，且這兩個三角形在OP的異側(cè)？若存在，請求出所有符合條件的點P的坐標；若不存在，請說明理由．

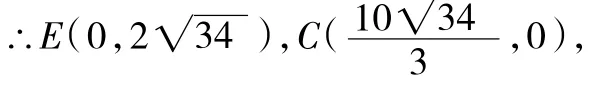
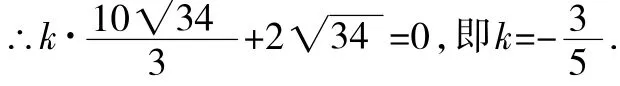
所以EG=6，OG=10，

（3）要使以O(shè)，P，Q為頂點的三角形與△OFP全等，且這兩個三角形在OP的異側(cè)，則只存在兩種情況：即OF=OQ或OF=PQ．

①當OF=OQ時，以O(shè)為圓心，OF長為半徑畫圓，確定點Q的位置（如圖3、4），作∠FOQ的角平分線確定P點.

當點Q在AC上（如圖3），由（2）知OG=10，則點G與點Q重合.

由△OP1F≌△OP1Q1，則有P1Fx軸，

由于點P1在直線AC上，

當x=10時，

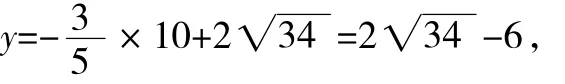
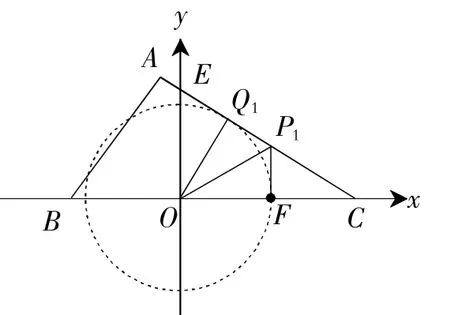
圖3

設(shè)OH=a，則BH=QH=14-a.

在Rt△OQH 中，a2+（14-a）2=102，解得a1=6，a2=8，

所以Q2（-6，8）或Q3（-8，6）．

連接QF交OP2于點M，則M是QF的中點，

當匝3（-8，6）時，則點1（1，3）．

設(shè)直線OP2的解析式為y=kx，把M（2，4）代入，解得k=2，

所以y=2x．

圖4

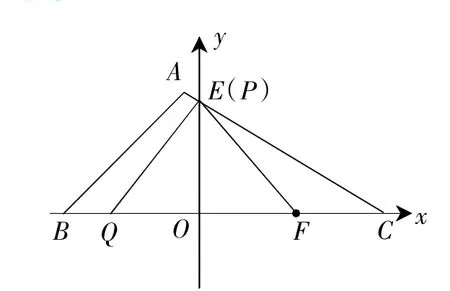
圖5

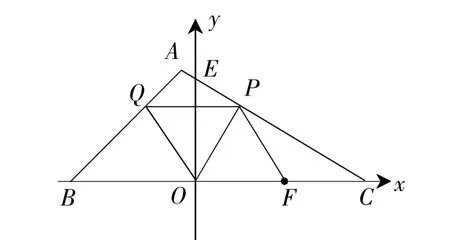
圖6

當M1（1，3）時，同理可求得

當Q在BC邊上（如圖5），OQ=OF=10，點P4在E點，

②當OF=PQ，QP∥OF時（如圖6），顯然四邊形OFPQ是平行四邊形，

設(shè)P的橫坐標為x，則點Q的橫坐標為x-10.

因為yP=yQ，又可求得直線AB的函數(shù)解析式為y=x+14，

綜 上 所 述 ， 滿 足 條 件 的 P點 坐 標 為

點評：構(gòu)造輔助圓，可使隱性問題顯性化，由三角形全等，確定思維方向，從而解問題．