考慮異常值的基于數學規劃法的案均賠款法

閆春+張靜+蘇瑞

摘 要：在存在異常值的情況下，非壽險公司應用傳統案均賠款法估計準備金常出現估計精度不高的問題。在分析傳統案均賠款法中進展因子和結案率估計方法的缺陷之后，引入數學規劃法對估計方法進行改進，建立進展因子和結案率的二次規劃和目標規劃模型，并引入權重因子弱化異常數據對進展因子和結案率估計結果的影響，運用一組流量三角形數據進行實證分析，結果表明：數學規劃法可以有效估計進展因子和結案率，弱化異常數據對準備金估計結果的影響。

關鍵詞： 案均賠款法；異常數據；數學規劃法

中圖分類號：F840.65 文獻標識碼： A 文章編號：1003-7217（2017）03-0046-06

一、引 言

未決賠款準備金是非壽險公司準備金估計中最重要的部分，公司的經營業績和經營風險受準備金估計值的影響顯著。存在異常數據時，非壽險公司應用傳統準備金估計方法估計的未決賠款準備金存在較大偏差。因此，為減弱異常數據對未決賠款準備金估計的影響，保證最終估計結果的準確度，有必要對流量三角形中的異常數據進行診斷并弱化其影響。

在準備金評估異常數據的診斷方面，國外學者最先進行了一些開創性研究。Carroll和Pederson（1993）在廣義線性模型（GLM）框架下對準備金估計模型受原始數據中異常值的影響程度進行了研究[1]。Preisser和Qaqish（1999）在廣義估計方程（GEE）的一般框架下，考慮了一類穩健估計量[2]。Cantoni和Ronchetti（2001）在GLM框架下應用擬似然估計方法提出一種穩健推斷工具，最終得到有界的預測值的影響函數[3]。Verdonck等（2009）在多種準備金估計方法中考慮了異常數據的影響，討論了鏈梯法中穩健性問題，并提出了穩健鏈梯模型[4]。Verdonck和Debruyne（2011）對廣義線性模型下準備金估計結果對異常數據的敏感程度進行了定量分析，構造診斷方程，并有效識別了流量三角形中異常值的位置[5]。之后，Anderson Paulo等（2014）也對穩健估計量進行深入探討，對穩健統計進行了廣泛研究[6]。

在國內，雖然這方面的相關研究開展得較晚，但也出現了很多成果。逯敏（2013）基于對鏈梯法的改進，引入穩健鏈梯模型和穩健廣義線性模型，并提出了兩階段的穩健廣義線性模型[7]。段白鴿、張連增（2014）考慮了一種穩健鏈梯模型，擴大了異常值的檢索范圍，減小了異常值對索賠準備金估計的影響[8]。盧志義等（2015）在鏈梯法中建立二次規劃和目標規劃模型對進展因子進行估計，引入權重因子，并應用一組模擬數據對所述方法進行實證分析[9]。閆春等（2015）在案均賠款法中考慮離群值的影響，運用殘差箱線圖法和兩點法對相關索賠數據進行離群值檢驗，然后針對離群值提出了一種穩健的案均賠款法[10]。

綜上，對于考慮異常數據影響的非壽險準備金的研究方法，主要集中于廣義線性模型及穩健鏈梯模型等，并且對于準備金評估方法的改進大多是針對鏈梯法的，而案均賠款法在鏈梯法的基礎上增加了案件數信息，使評估信息更加充分，但目前國內外對案均賠款法的研究成果比較少。鑒于此，本文在傳統案均賠款法中考慮異常數據，首先，對其進行敏感性分析，并對進展因子和結案率估計方法的不足進行簡要說明，提出數學規劃法對進展因子和結案率建立二次規劃模型和目標規劃模型。然后，在此模型下同時引入權重因子，分別對進展因子和結案率進行估計，區別不同數據信息對估計結果的作用，將此類方法與傳統案均賠款法結合，弱化異常數據對進展因子和結案率估計的影響，從而保證未決賠款準備金估計的準確度。最后，應用一組經典數據對所述的方法進行驗證，比較分析最終的估計結果。

二、案均賠款法準備金評估及敏感性分析

案均賠款是賠款與案件數的比值。基本假設：各事故年的案均賠款保持著相對穩定的趨勢。案均賠款法根據是否已經結案可以分為已報案案均賠款（PPCI）和已結案案均賠款（PPCF）。本文以PPCF法為例，進行詳細介紹及模型構建。

PPCF方法應用累計已報案件數Ni，j流量三角形、累計已結案件數Di，j流量三角形和增量已結案賠款Yi，j流量三角形對準備金進行估計。具體步驟為：第一，預測最終已報案案件數。對累計已報案件數Ni，j流量三角形應用鏈梯法預測各事故年的最終案件數。第二，計算已結案案件數。從累計已報案案件數中減去未結案的案件數即可得到最終已結案案件數。第三，預測未來的已結案案件數。首先，計算結案率及其平均值，結案率是指已結案的累計案件數在已報案的總案件數中所占的比重，其計算公式為：vi，j=Di，j/Ni，n。其中，Ni，n表示事故年i發生的保險事故所導致的總索賠次數。計算出結案率以后，選定結案率的平均值作為各進展年的結案率，且尾部結案率估計值假定為1。然后，預測未來已結案的案件數，根據結案率的選定值乘以總索賠次數，計算出年末累計已結案索賠次數的預測值，用后一個進展年的結案次數減去前一個進展年的結案次數，得到增量已結案件數流量三角形i，j。第四，計算案均賠款。將已結案賠款與已結案案件數相除，計算公式為：i，j=Yi，j/i，j。同樣，運用鏈梯法預測已結案案均賠款流量三角形i，j的下三角部分。第五，估計未決賠款準備金。將已結案均賠款與已結案件數一一對應相乘可得到未決賠款的預測值，未決賠款預測值流量三角形下三角部分的數據加總可得到最終的未決賠款準備金。

可以看出，案均賠款法是一種鏈梯模型，但其同時兼顧案件數（頻率）和賠款額（強度）兩種信息，核心問題是計算案均賠款。

案均賠款法隱含的基本假設是不同事故年的案均賠款相對穩定，但在實際的非壽險數據中并不總能得到滿足。當流量三角形中數據出現異常值時，使用案均賠款法評估準備金，將會對準備金的估計結果產生較大影響。因此，對流量三角形中的數據進行檢測是否存在異常值至關重要。

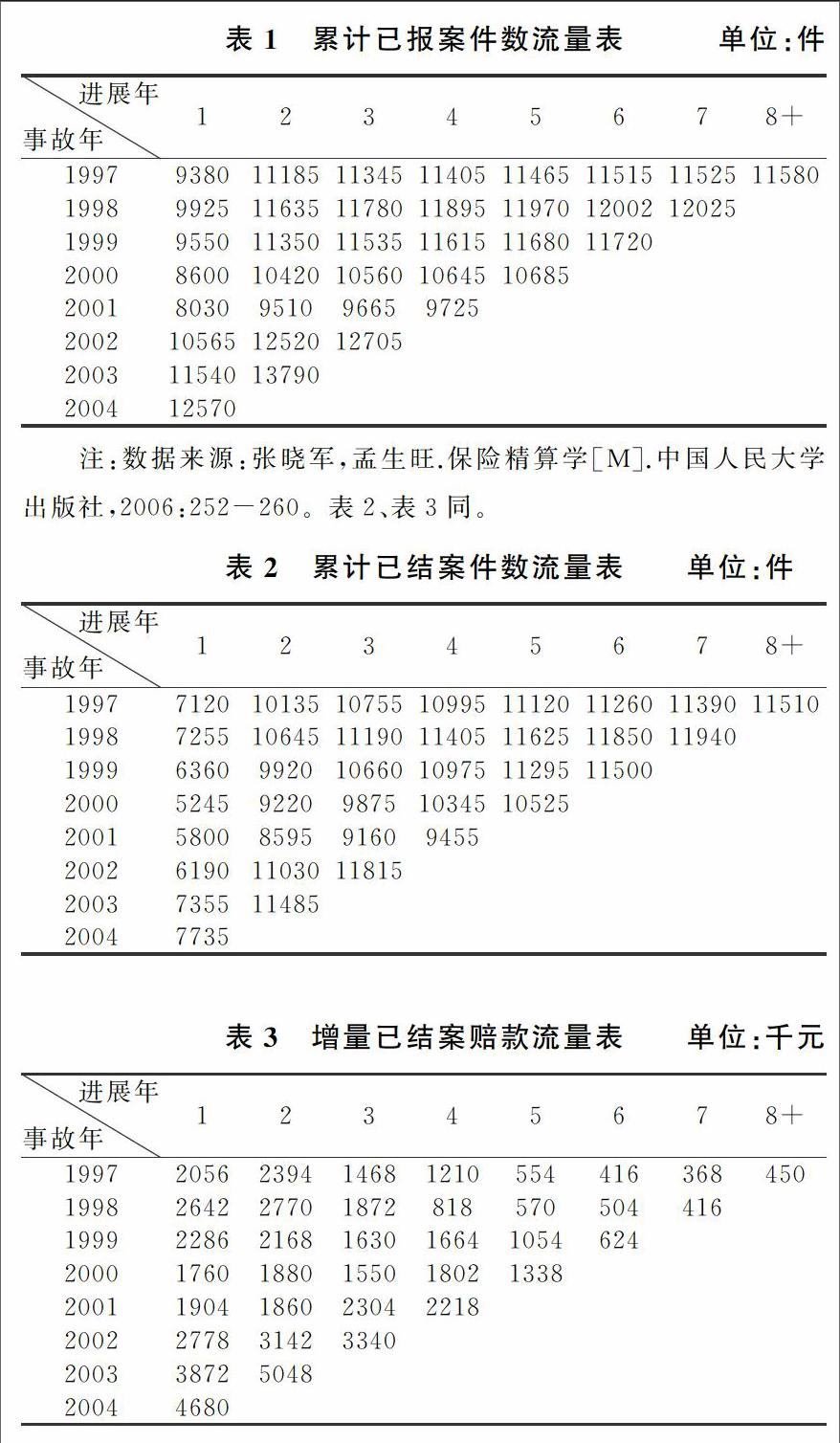
下面選取張曉軍、孟生旺《保險精算學》里的一組數據，來驗證并分析案均賠款法對異常數據的敏感程度[11]，見表1～3。其中，表1為累計已報案案件數Ni，j，表2為累計已結案案件數流量表Di，j，表3為增量已結案賠款流量表Yi，j。

對表1數據應用鏈梯法得到流量三角形的下三角部分，預測各事故年的最終案件數，再求得結案率。根據結案率數據，可以用各事故年最終的累計已報案件數分別乘以對應進展年的結案率的選定值，即可求得累計已結案索賠次數流量三角形的下三角部分；然后，將累計已結案案件數流量表轉化為增量已結案案件數流量表；最后，用表3的賠款數據除以增量已結案案件數上三角部分，即可得到已結案案均賠款流量。

對已結案均賠款流量表應用鏈梯法得到未來各年已結案均賠款的預測值，用已結案均賠款預測值乘以已結案索賠次數預測值，即可得到未決賠款準備金的估計值。

為了探究異常賠款數據對傳統案均賠款法準備金估計值的影響程度，對表2中事故年為1999年、進展年為3的已結案案件數縮小10倍進行異常化處理，得到新的結案率。然后，按照傳統的PPCF模型對準備金進行估計，得到沒有異常值情況下的估計結果為71 095千元，存在異常值情況下的結果為187 506千元。

比較數據可知，將表2中的已結案案件數流量表中的某一數值設為異常數據后，存在異常值情況準備金估計值比不存在異常值情況下估計值增加了1倍多，而且這只是在存在單一異常數據的情況下比較結果得出的差異。由此可見，傳統的案均賠款法受異常值的影響程度較大，需要我們探索一種新的方法來降低其對異常數據的敏感性。

三、數學規劃法估計進展因子和結案率

由于傳統的案均賠款法對準備金的估計結果容易受異常數據的影響，為此，對該方法的這一缺陷進行改進，弱化異常數據對結案率及進展因子的影響。考慮到數學規劃法的研究對象是數值的最優化問題，解決的主要問題是在給定條件下，按某一衡量指標來尋找安排的最優方案，可表示成求函數在滿足約束條件下的極大極小值問題，其優點是可將復雜過程通過映射直觀反映于目標函數，建立相應的數學模型從而優化最終的估計結果[12]。我們將進展因子和結案率的偏差函數最小作為目標函數，嘗試建立二次規劃模型和目標規劃模型，并引入權重因子對進展因子和結案率進行估計，同時，也可以在該數學規劃模型的約束條件中加入有關進展因子和結案率的其他相關信息，使進展因子和結案率的估計值更穩健，從而提高準備金估計的精確度。

（一）傳統案均賠款法進展因子和結案率的估計及不足

由式（1）可看出，用原始加權法得到的進展因子是各事故年逐年進展因子的加權和。這種方法估計的進展因子受流量三角形中數據的影響程度較大，即對數據變化較為敏感，并且不能反映不同的數據信息對進展因子估計的不同作用，也不能有效降低進展因子估計值對異常數據的敏感性。

在已結案均賠款法中，結案率vi，j的值受累計已結案流量三角形Di，j和累計已報案流量三角形Ni，j的影響，若兩個流量三角形中有一個出現異常數據都會導致結案率出現異常。由此可知，結案率對觀察值的變化敏感性較高，結案率的異常也必然會影響最終的準備金估計結果。

針對案均賠款法中進展因子和結案率估計不足的缺陷，下面運用最優化理論方法給出最優進展因子和最優結案率的評價標準，并將此標準作為目標函數，建立二次規劃和目標規劃模型對進展因子和結案率進行估計。

（二）二次規劃法①[13]優化進展因子和結案率

在案均賠款法假設條件下，數學規劃法確定進展因子和結案率的思想是：在特定進展模式下通過最小化誤差的平方和找到一組數據的最佳函數匹配。

1.二次規劃法優化進展因子模型。

其中，v*i，j=Di，j+d+*i-d-*iNi，n是經過校正后的結案率。從式（15）可以看出，偏差函數的絕對值可以很好地衡量結案率估計方法的優劣性和可行性，并且目標規劃法使得偏差函數絕對值總和達到最小。同二次規劃法一樣，結合了目標規劃法的案均賠款法更具有靈活性和適用性。加權二次規劃法和加權目標規劃法在原有方法的基礎上引入了權重因子，可以反映不同日歷年數據對進展因子和結案率估計的影響程度，這使得進展因子和結案率的估計值更加符合較近日歷年賠款模式，選擇對應的權數也增強了估計的穩健性，弱化了異常數據對準備金估計結果的影響。

四、實證分析③

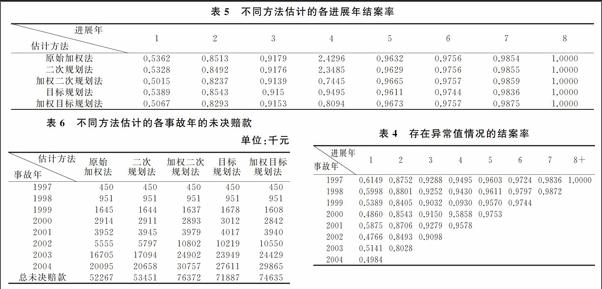
已知表1和表2中的數據是不存在異常數據的，為了驗證數學規劃法對異常數據的弱化作用，提高準備金估計的準確度，需要通過對比添加異常值后的改進案均賠款法和傳統案均賠款法結案率估計值及最終賠款估計值的差異，來度量兩種方法對異常數據的敏感性。將表2事故年1999年、進展年4的數據縮小10倍，事故年2000年、進展年4的數據擴大10倍作為異常數據，該數據可以解釋為人為輸入有誤所致，得到表4即存在異常值情況下的結案率。

權數的選取采用如下方法進行：由方程∑n-j+1k=1wk=1解得w各事故年對應相應的權數，對于高階方程可以使用Matlab進行求解。在實務中，權數的選取要有依據，例如表4中進展年4的結案率，事故年1999年的數據明顯偏小，而事故年2000年的數據明顯偏大，可以看作異常數據，在選取權數時，為避免該異常數據對結案率估計的影響，事故年1999年應賦予較大權重，事故年2000年應賦予較小權重。其次，考慮日歷年因素，較近日歷年賦予較大權重。解方程∑5k=1w5=1得w=0.5087，選取各事故年相應的權數為0.0669、0.1316、0.5087、0.0341、0.2587。根據不同方法估計的結案率如表5所示。

由表5可以看出，用二次規劃法估計的各進展年的結案率與原始加權法得到的結案率估計值相差不大，對進展年4的異常結案率也沒有做出相應的修正，而目標規劃法的估計結果對異常結案率進行了較好的修正。同時可以發現，加權二次規劃法和加權目標規劃法對結案率的估計結果也相差不大，對于進展年4的結案率估計時，對事故年1999年的結案率賦予較大權數，對事故年2000年的結案率賦予較小權數，從而加權二次規劃法和加權目標規劃法有效降低了結案率估計的敏感性，減弱了異常數據對結案率估計的影響，同時，權數的選取也體現了較近日歷年準備金的進展模式。

分析表6可知，二次規劃法雖然為結案率的估計給出了明確的目標函數，使得估計方法更加靈活，但當數據中存在較大（小）異常數據時，二次規劃法求得的最終賠款準備金的準確度與原始加權法相差不大，對異常數據較敏感，估計準確度較低。而考慮了權數的二次規劃法，則可以對結案率的估計進行“修勻”，使得到的估計值受異常數據的影響較小。目標規劃法和加權目標規劃法較其它估計也可以弱化異常數據對結案率估計的影響，從而提高準備金估計的準確度，使準備金估計更加合理。并且加權二次規劃法和加權目標規劃法在選取權數方面考慮日歷年因素，較近日歷年選取較大權數，區分不同信息對結案率和進展因子估計的作用。

五、結 論

以上采用數學規劃法對傳統案均賠款法中的進展因子和結案率進行估計，結果顯示：（1）設定明確的目標函數對進展因子和結案率進行估計，并在此目標函數下運用二次規劃模型和目標規劃模型可以估計出最優的進展因子和結案率。（2）簡潔靈活的數學規劃法作為進展因子和結案率估計的優化方法，可充分利用歷史賠款數據，有效提高約束條件的可靠性，得到優化的估計結果。（3）考慮到權重因素，在目標函數中引入權重因子，反映出進展因子和結案率的估計值受不同的數據信息的影響程度，從而可以體現其對不同日歷年數據的偏重程度，降低準備金估計結果對異常數據的敏感性，從而為進展因子和結案率的估計提供了更加靈活的方法。

注釋：

①二次規劃法是指目標函數是二次函數、約束條件為線性等式或不等式約束的數學規劃問題。二次規劃是線性規劃問題向非線性規劃問題的自然過渡，是最早研究的一類非線性規劃問題，同時也是一類非常重要的約束優化問題，在實際中應用廣泛。

②目標規劃是對一組目標進行優化，并且考慮目標的優先順序因素，尋找在多個預定目標前提下的滿意解（通常稱為最優解），使得計算得到的目標值盡量達到預定目標值，亦即使實際目標值與預定目標值之差的偏差變量的取值最小。目標規劃法是在一般線性規劃和多目標規劃的基礎上發展起來的一種數學規劃法，其數學模型由求極小值的達成函數和約束條件構成。

③這里仍采用張曉軍、孟生旺《保險精算學》里的數據對本文所述的數學規劃模型進行驗證和對比。

參考文獻：

[1]Carroll R J，Pederson S.On robustness in the logistic regression model[J].Journal of the Royal Statistical Society，Series B，1993，55（3）：693-706.

[2]Preisser J S，Qaqish B F.Robust regression for clustered data with applications to binary regression[J].Biometrics 1999，55（2）：574-579.

[3]Cantoni E，Ronchetti E.Robust inference for generalized linear models[J].Journal of the American Statistical Association，2001，96（455）：1022-1030.

[4]Verdonck T，Van Wouwe M，Dhaene J.A robustification of the chain-ladder method[J].North American Actuarial Journal，2009，13（2）：280-298.

[5]Verdonck T，Debruyne M.The influence of claims on the chain-ladder estimates：analysis and diagnostic tool[J].Insurance：Mathematics and Economics，2011，48（1）：85-98.

[6]Anderson Paulo de Paiva，José Henrique F.A multivariate robust parameter optimization approach based on principal component analysis with combined arrays [J].Computer&Industrial Engineering，2014（74）：186-198.

[7]逯敏.保險公司異常賠款數據對準備金估計的影響研究[D].天津：天津財經大學，2013.

[8]段白鴿，張連增.考慮離群值的穩健鏈梯法[J].數理統計與管理，2014（7）：1-21.

[9]盧志義，劉樂平，張慧.鏈梯法中進展因子估計的數學規劃法[J].數學的實踐與認識，2015（5）：249-255.

[10]閆春，李延星，孫曉紅，劉志博.考慮離群值的非壽險準備金案均賠款法[J].保險研究，2015（11）：15-24.

[11]張曉軍，孟生旺.保險精算學[M].北京：中國人民大學出版社，2006：242-260.

[12]智庫百科.數學規劃[EB/OL].http：//wiki.mbalib.com/wiki/%E6%95%B0%E5%AD%A6%E8%A7%84%E5%88%92，2016-10-12.

[13]黃正海，苗新河.最優化計算方法[M].北京：科學出版社，2015：132-135.

[14]江道琪，何建坤，陳松華.實用線性規劃方法及其支持系統[M].北京：清華大學出版社，2006：259-264.

（責任編輯：寧曉青）

Abstract：In the presence of outlying values，the traditional payments per claim method of estimating reserving in non-life insurance companies lack accuracy.First，the drawbacks of traditional payments per claim method in progress factors and settlement rate are analyzed briefly.Then introduced mathematical programming into the estimation method，and quadratic programming and objective programming are established to estimate progress factors and settlement rate.Meanwhile，weight is proposed to abate the influence of the outlying values in the estimate of the progress factors and settlement rate，and using a set of run off triangle data to provided.The results has shown that the mathematical programming method can effectively estimate progress factor and settlement rate，weakening the influence of outlying values on the estimation of reserves.

Key words：Payments per claim method；Outlying values；Mathematical programming method