應用均值換元法解高考最值問題
江蘇省泰州市姜堰區蔣垛中學 (225503) 徐愛芳
應用均值換元法解高考最值問題
江蘇省泰州市姜堰區蔣垛中學 (225503)
徐愛芳
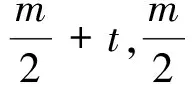
1.應用均值換元法解最大值問題
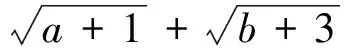
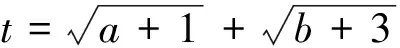
評注:此題從表面上看似乎與均值換元無關,使人陷入“山窮水盡疑無路”之境,但仔細觀察題目條件的特點,充分展開聯想,經過變形化簡,發揮思維的創造性,利用不等式簡捷明快地求得了最大值,可謂解法靈活巧妙,思路匠心獨具,不得不令人拍案叫絕.
2.應用均值換元法解最小值問題
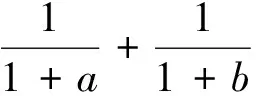
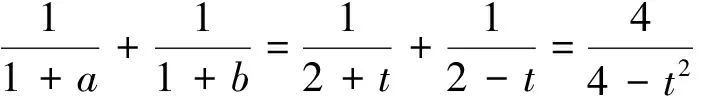
評注:本題由a+b=2,直接聯想到平均值換元,思路明析,目標明確,方法簡捷,別具風味.
3.應用均值換元法解最大值和最小值問題
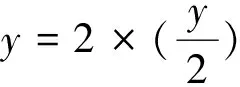
評注:本題如用常規方法求最大值,可將原式兩邊平方后,通過化簡變形去尋找解題途徑,然而應用均值換元解,不僅方法新穎,而且簡捷別有風味.本題解法的巧妙之處在于通過均值換元后,大大減少了計算量,降低了解題的難度,充分顯示了均值代換的優越性.
例4 (2010年浙江大學自主招生考試題)設x,y≥0,2x+y=6,求z=4x2+3xy+y2-6x-3y的最大值和最小值.
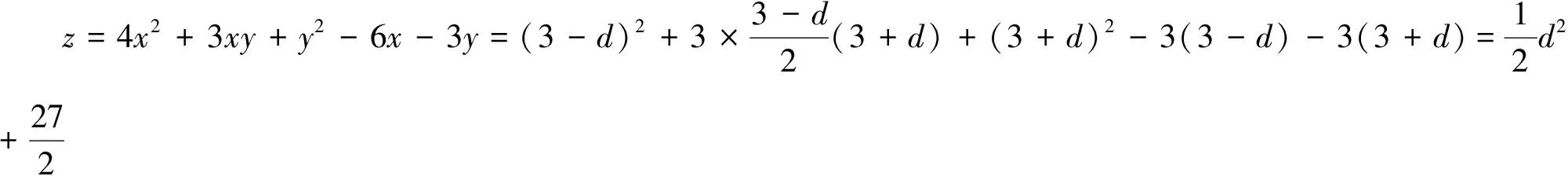
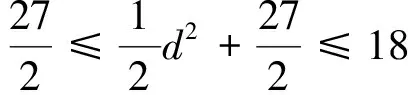
評注:本題用一般的思維方式考慮,很難找到解題的方法或是過程相當復雜,而通過2x+y=6=3+3,聯想我們設2x=3-d,y=3+d,從而溝通了題設與結論的關系,使問題輕松得到解決,此法不僅別具一格,方法新穎,而且解題過程充分體現了均值換元思想的應用價值,更加顯示出均值代換在解題中的重要作用.
例5 (江蘇省蘇北四市2015年春高三一模試題)設x、y、z為非負數,且x+y+z=1,求xy+yz+zx-2xyz的最大值和最小值.
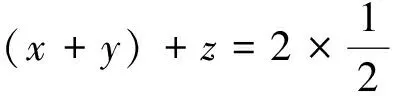
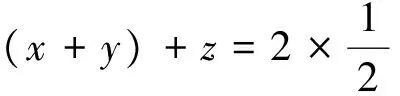
縱觀以上五例可以看出應用均值換元法求最大(小)值,其關鍵是要從問題的背景出發,根據題設及所求題目的結構特征經過合理的推理,探究出問題中隱藏的均值關系,列出符合題意的關系式,以達到解題的目的.
[1]趙春,孫健.應用均值代換法智解競賽最值問題.中學數學雜志(高中版)2016,1.
[2]于志洪.應用三角換元法解競賽最值問題.數學通訊(上半月).2015,4.

