用基本不等式巧證2017年數學奧林匹克試題

江西省南昌市第十四中學 (330003) 吳倩倩

用基本不等式巧證2017年數學奧林匹克試題

江西省南昌市第十四中學 (330003)
吳倩倩

本文旨在給出2017年國際數學奧林匹克不等式題的巧妙且通俗的證明，供老師和同學學習和參考.

例1 (2017年土耳其數學奧林匹克)已知a,b,c是滿足a+b+c=3的正數，求證：a3b+b3c+c3a+9≥4(ab+bc+ca).

證明：由均值不等式可得a3b+b3c+c3a+9=a3b+b3c+c3a+(a+b+c)2=(a3b+b2)+(b3c+c2)+(c3a+a2)+2(ab+bc+ca)≥4(ab+bc+ca).

注1：此題證明的關鍵是大方向明確，依序進行.

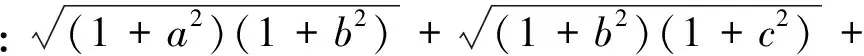
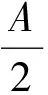
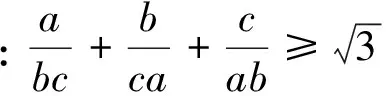
注3：合理分析，步調一致.

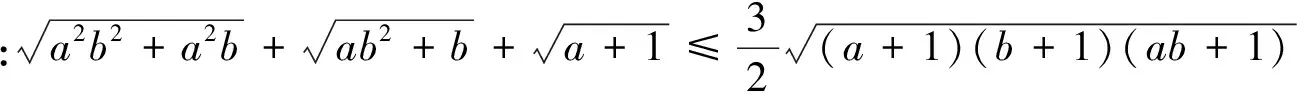
證明：由均值不等式可得

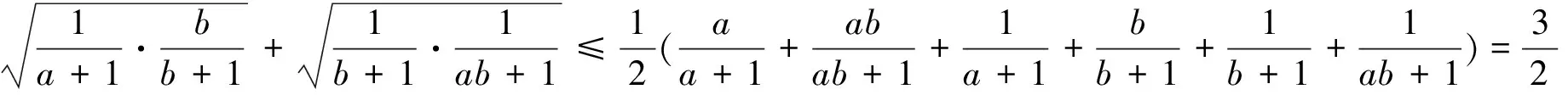
注4：還是恒等變形唱主角.

例5 (2017年摩爾多瓦數學奧林匹克)

已知n是正整數，求證：

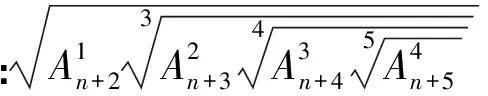
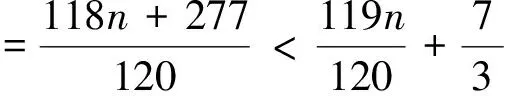
注5：做題得細心,而且要有耐心.

例6 (2017年IMO中國國家隊選拔考試三試題1)已知x1,x2,…,xn(n≥4)是滿足x1+x2+…+xn=1的非負實數，求x1x2x3+x2x3x4+…+xnx1x2的最大值.

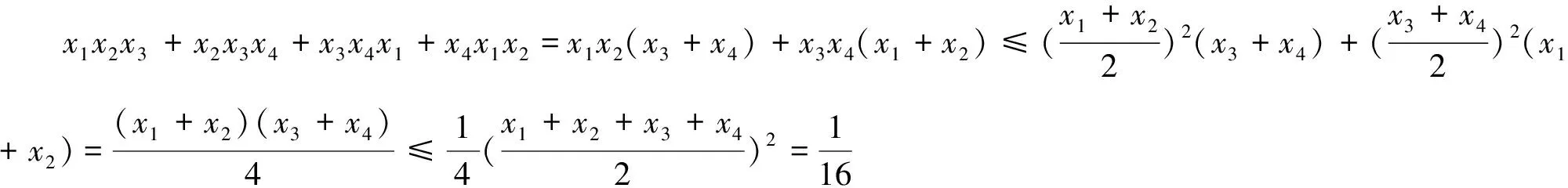
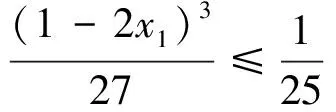
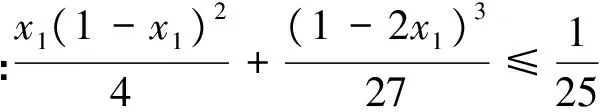
注6：題目雖然難，但是證明的工具只是基本不等式.