圓珠筆頭自動裝配過程中強度的有限元分析

李恒，李正軍，胡鼎，楊雷

(山東省科學院海洋儀器儀表研究所，山東 青島 266000)

?

【新材料】

圓珠筆頭自動裝配過程中強度的有限元分析

李恒，李正軍，胡鼎，楊雷

(山東省科學院海洋儀器儀表研究所，山東 青島 266000)

針對圓珠筆裝配中出現(xiàn)筆頭斷裂破損的情況，運用Pro/Engineer建立了圓珠筆頭及其裝配設(shè)備的3D模型，并通過有限元軟件ANSYS對其進行分析。利用數(shù)據(jù)采集系統(tǒng)采集筆頭在裝配各個階段的受載，再通過ANSYS對其進行應(yīng)力分析，找出最大應(yīng)力和應(yīng)力集中位置，并進行相關(guān)的實驗，驗證了有限元分析的正確性，得出了筆頭破壞的原因，最終提出了具有可行性的解決方案。

圓珠筆;圓螺紋連接；受力研究;有限元分析;解決方案

中國的圓珠筆裝配設(shè)備處于一個低水平的階段，其中一個顯著的問題是大量模仿國外設(shè)備進行設(shè)計。雖然這種做法取得了一定的成效，但是在模仿設(shè)計的過程中，只注重結(jié)構(gòu)功能的模仿，不注重機理性的研究，對設(shè)計中的受載情況和動態(tài)性能等方面缺乏相應(yīng)的數(shù)據(jù)支持[1-2]。

在傳統(tǒng)的筆頭連接方式當中，圓螺紋連接應(yīng)用很常見，但是針對圓螺紋裝配連接的應(yīng)力應(yīng)變分析卻非常少。現(xiàn)有的螺紋應(yīng)力應(yīng)變測量方法，成本非常高，對儀器要求嚴格，難以實現(xiàn)。有限元分析在制造業(yè)中的應(yīng)用越來越廣泛[3-5],但利用有限元分析來研究圓珠筆裝配設(shè)備的工程問題，在國內(nèi)還很少見[1]。應(yīng)用有限元方法與全尺寸實驗相結(jié)合，分析圓螺紋連接的應(yīng)力分布，可以對螺紋連接做出精確的應(yīng)力、應(yīng)變分析，為優(yōu)化圓珠筆頭的螺紋裝配環(huán)節(jié)提供理論數(shù)據(jù)支持。

1 有限元模型及輸入條件

1.1 圓螺紋筆頭三維模型的建立

有限元分析計算的精度與模型有很大關(guān)系，目前，對于螺紋的有限元模型的建立，國內(nèi)外研發(fā)技術(shù)人員通常采用下列三種方法[6]：

(1)梁單元模型。采用梁單元來模擬實際的螺紋連接，在分析中可以大量地節(jié)省計算機的資源，但因其未考慮螺紋的一些細節(jié)，應(yīng)力的大小、應(yīng)變的分布計算結(jié)果誤差較大，應(yīng)用范圍很小。

圖1 螺紋的三維螺旋模型Fig.1 Three-dimensional spiral model of thread

(2)二維軸對稱模型。對模型軸進行對稱性的分析，把實際的三維問題轉(zhuǎn)化為相對簡單的二維問題來進行研究。運用該模型對二維軸對稱結(jié)構(gòu)的分析，其結(jié)果雖有誤差但卻不大；對非軸對稱結(jié)構(gòu)的分析考慮了螺紋的細節(jié)，但是卻忽視了螺旋效應(yīng)對結(jié)果的影響，而且假定對稱加載，無法用于載荷偏置的場合，計算結(jié)果誤差較大。

(3)三維軸對稱模型與三維螺旋模型。三維軸對稱模型能在載荷偏置的場合應(yīng)用，但是忽略了螺紋升角對模型的影響。三維螺旋模型，是按照實際尺寸做出螺紋連接模型，可以得到零件精確的應(yīng)力、應(yīng)變分布，計算非常準確，但是模型十分復(fù)雜，自由度很多，導(dǎo)致計算量太大，計算時間長，成本非常高[7-8]。

考慮到圓螺紋筆頭在裝配中受到的復(fù)雜的載荷情況，我們不能采用簡化的模型，于是選擇了三維螺旋的螺紋模型。如圖1所示。

1.2 有限元分析輸入條件

1.2.1 材料參數(shù)

圓珠筆頭和筆桿的材料是PP塑料，其破壞強度值是272 MPa。主軸材料是45號鋼，還有一些橡膠，對其質(zhì)量進行了等效處理，采用的參數(shù)同45號鋼，其破壞強度值是600 MPa。相關(guān)參數(shù)見表1和表2。

表1 PP材料的具體參數(shù)

表2 45鋼的具體參數(shù)

1.2.2 網(wǎng)格處理

在網(wǎng)格劃分時，采用ANSYS Workbench的自動網(wǎng)格劃分。將筆頭分成26 578個單元，主軸系統(tǒng)分成了36 784個單元，網(wǎng)格劃分如圖2所示。

圖2 ANSYS-Workbench網(wǎng)格劃分Fig.2 ANSYS-Workbench mesh generation

1.2.3 約束和載荷

在筆頭與筆桿對應(yīng)位置添加摩擦和固定約束，在主軸上相應(yīng)的位置處添加軸承的約束。

圓珠筆頭在裝配中所承受的載荷是多方面的，包括旋轉(zhuǎn)工作頭施加的沖擊力、壓力、扭矩、慣性力、離心力以及振動而引發(fā)的載荷等。在其裝配的各個階段，受到的載荷是不同的。通過分析，我們確定筆頭破壞最有可能發(fā)生在兩個受載比較大的階段，即裝配的前期和后期。

為確定筆頭在各個階段的受載情況，對于能夠直接測量的載荷，應(yīng)用LabVIEW編寫了數(shù)據(jù)采集主界面，然后應(yīng)用NI數(shù)據(jù)采集系統(tǒng)采集該圓珠筆裝配設(shè)備在筆頭的裝配過程中，在不同階段筆頭所受的力、扭矩等載荷。對于不能直接測量的載荷，應(yīng)用測速儀和高清相機測量筆頭的轉(zhuǎn)速和加減速時間，計算動載荷、離心力等載荷。其中，數(shù)據(jù)采集系統(tǒng)如圖3所示。

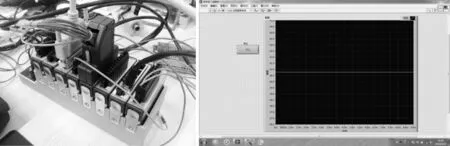
圖3 數(shù)據(jù)采集系統(tǒng)Fig.3 Data collection system

在裝配的前期，圓珠筆頭受到旋轉(zhuǎn)工作頭的沖擊力，該力大小基本是穩(wěn)定的，我們進行了24次測量，得到了裝配前期的24組沖擊力的數(shù)據(jù)，對這些數(shù)據(jù)值進行了分析，統(tǒng)計結(jié)果如表3所示。

表3 初始階段沖擊力的24次采樣數(shù)據(jù)統(tǒng)計結(jié)果

最終，選擇最大的沖擊力22.65 N作為裝配前期分析所用的壓力。

在裝配的后期，圓珠筆頭承受的載荷是多方面的，主要包括旋轉(zhuǎn)工作頭施加的壓力、主動扭矩、慣性力、離心力等，我們選擇測量和計算其中最主要的壓力載荷和動載荷。在裝配的最后階段，我們同樣進行了24次測量，得到了裝配后期的24組沖擊力的數(shù)據(jù)統(tǒng)計結(jié)果，如表4所示。

表4 最后階段壓力的24次采樣數(shù)據(jù)統(tǒng)計結(jié)果

最終，選擇最大的沖擊力19.7 N作為裝配后期分析所用的壓力。

圓珠筆頭裝配是一個先加速再減速到停止的過程，在這個過程中，會出現(xiàn)一個最高的轉(zhuǎn)速，在減速到停止的過程中，會出現(xiàn)動載荷。我們先用測速儀測量筆頭在裝配中的最高轉(zhuǎn)速，一共測了10組數(shù)據(jù)，因為動載荷是影響圓珠筆裝配質(zhì)量的重要因素，所以對測得的10組數(shù)據(jù)不進行統(tǒng)計，而是分別記錄，這10組最高轉(zhuǎn)速的數(shù)據(jù)結(jié)果如表5所示。

表5 10組最高轉(zhuǎn)速數(shù)據(jù)Table 5 10 sets of data for the highest speed

利用高速相機拍攝筆頭的減速過程，我們用軟件對圖片處理后得到一個筆頭裝配的完整過程,如圖4所示。

圖4 一個裝配周期圖Fig.4 An assembly cycle

減速時間為0.5 s，有了轉(zhuǎn)速和減速的時間，就能算出加速度值，再結(jié)合其他參數(shù)進行計算，我們得出了筆頭的10組慣性力矩的數(shù)值，結(jié)果如表6所示。

表6 10組慣性力矩數(shù)值

2 有限元模擬結(jié)果及分析

2.1 零件強度分析

2.1.1 裝配前期的靜力分析

工作頭對筆頭的作用力并不是穩(wěn)定不變的，而是有一些小幅的波動，但其大小基本是穩(wěn)定的，我們選擇最大的力22.65 N作為分析所用的壓力。約束和載荷施加完成后，執(zhí)行SOLVE命令開始計算求解。

圓珠筆頭處于初始階段時的應(yīng)力云圖，如圖5所示。

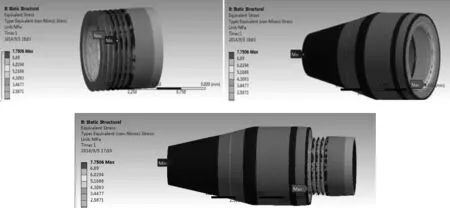
圖5 外螺紋和內(nèi)螺紋的應(yīng)力云圖(初始位置)Fig.5 Stress cloud chart of the external and internal thread

通過觀察應(yīng)力云圖，可知在圓珠筆頭初始階段時，最大的應(yīng)力值為7.750 6 MPa，應(yīng)力比較大的位置多集中在接觸的齒根圓上。由此可知，最大的應(yīng)力非常小，遠小于強度極限值，因此可以得出筆頭的破壞不在裝配初期，并不是由旋轉(zhuǎn)工作頭的沖擊力造成的。

2.1.2 裝配后期的動態(tài)分析

選擇最大的力19.7 N作為分析所用的壓力。通過計算，又得出了10組裝配后期施加在旋轉(zhuǎn)工作頭上慣性力矩，其中慣性力矩臨界值是264 N·mm，該臨界值的概念是指處在19.7 N的壓力和264 N·mm的扭矩下時，筆頭剛好處于破壞強度臨界點

10組慣性力矩中，有2組數(shù)據(jù)在仿真分析時其最大應(yīng)力值超過了材料極限強度，有1組數(shù)據(jù)正好處于臨界應(yīng)力值，即筆頭發(fā)生了不同程度破壞，其破壞位置正好與實際相符。筆頭在臨界破壞載荷下的應(yīng)力云圖如圖6所示。

圖6 外螺紋和內(nèi)螺紋的應(yīng)力云圖(最后位置)Fig.6 Stress cloud chart of the external and internal thread

通過觀察應(yīng)力云圖，可知在裝配圓珠筆頭最后階段時，最大的應(yīng)力值為332.78 MPa，應(yīng)力最大的部位與筆頭實際破壞的部位一致，即大端面的外沿。在計算破損率時，我們將臨界狀態(tài)視為已破壞，故10組測得的數(shù)據(jù)中有3組會導(dǎo)致筆頭破壞，故認為筆頭在裝配后期的破損率為30%。

2.2 旋轉(zhuǎn)主軸的模態(tài)分析

旋轉(zhuǎn)主軸是該筆頭裝配設(shè)備的關(guān)鍵部件，其動態(tài)特性很大意義上影響著筆頭裝配的質(zhì)量。主軸旋轉(zhuǎn)產(chǎn)生的振動是該設(shè)備的主要振動源，工作頭運轉(zhuǎn)的平穩(wěn)性對于圓珠筆頭的裝配質(zhì)量有著十分重要的影響[8-9]。

通過分析，得出該圓珠筆裝配設(shè)備的主軸系統(tǒng)的固有頻率，見表7。

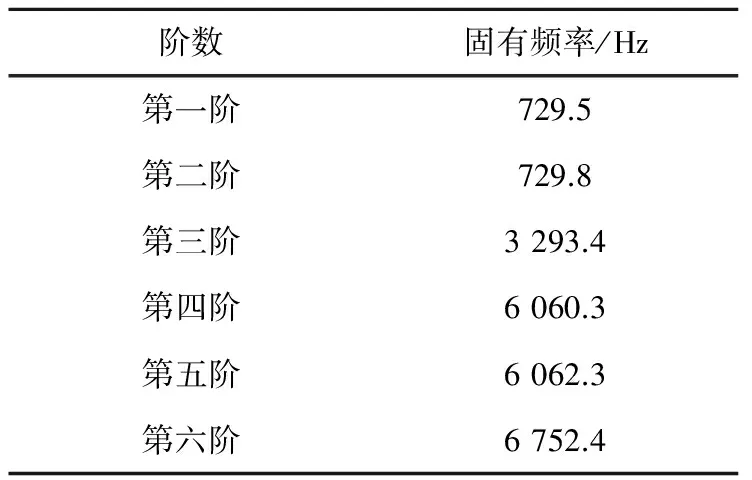
表7 主軸系統(tǒng)的固有頻率

主軸系統(tǒng)的前六階振型如圖7所示。

圖7 主軸系統(tǒng)的振型圖Fig.7 The vibration models of the spindle system

根據(jù)公式n=60f，其中f是系統(tǒng)的固有頻率，n是轉(zhuǎn)速，已知主軸系統(tǒng)的固有頻率，計算出各階的臨界轉(zhuǎn)速。主軸的工作轉(zhuǎn)速低于40 000 r/min，就可以有效地避開共振區(qū)。在實驗中利用測速儀測量圓珠筆生產(chǎn)線上正常工作主軸的轉(zhuǎn)速為3 000 r/min，主軸工作穩(wěn)定，不會造成筆頭的破壞。

2.3 解決方案

針對現(xiàn)有的問題，提出了更換彈簧的方法。在專配設(shè)備中，該處彈簧可以調(diào)整壓力的大小，直接改變壓力值，間接改變了動載荷，對動載荷的影響在于摩擦力變小，減速停止的時間變長，從而動載荷和減小了。這個方法簡單易實現(xiàn)，不會提高成本，而且工作可靠。通過更換一個彈性系數(shù)更小的彈簧，可以同時降低筆頭在裝配后期受到的3個載荷的值，降低了筆頭在裝配中的破損率，提高了圓珠筆的合格率。

針對彈簧的選擇，我們應(yīng)用不同彈性系數(shù)的彈簧進行實驗，記錄其破損率。對筆頭進行速度的測量，并利用1.2.3節(jié)提到的方法進行載荷的計算，與我們得出的臨界載荷的數(shù)據(jù)進行對照。彈簧的彈性系數(shù)不能太低，在小到一定數(shù)值時，就不能保證筆頭的正常裝配了。最終得到一個最優(yōu)的彈性模量的范圍值為0.6～0.8 N/mm。

3 結(jié)語

針對圓珠筆頭在裝配中出現(xiàn)筆頭斷裂破損的情況，建立了圓珠筆頭和圓珠筆頭裝配設(shè)備的3D模型，并通過有限元軟件ANSYS Workbench對其進行強度分析和動態(tài)分析。找出了最大應(yīng)力和應(yīng)力集中位置，得出了筆頭破壞的原因，最終提出了具有可行性的解決方案。本文對于改進圓珠筆生產(chǎn)加工設(shè)備，提高圓螺紋接頭的連接質(zhì)量，促進圓珠筆裝配設(shè)備的研發(fā)具有積極的意義。

[1]馬云虎. 我國圓珠筆工業(yè)的現(xiàn)狀和發(fā)展方向[J]. 中國制筆, 1995(3/4)：22-24.

[2]施偉, 李夢甦, 吳文英. 我國制筆業(yè)和裝備的現(xiàn)狀及發(fā)展趨勢[J]. 中國制筆, 2005 (3): 38-41.

[3]高斌, 宋小文, 盧斌, 等. 發(fā)動機氣缸體螺紋聯(lián)接強度有限元分析[J]. 工程設(shè)計學報, 2005, 12(4): 227-231.

[4]夏衛(wèi)明, 鄭翔, 楊曉俊, 基于ANSYS的盲孔螺栓聯(lián)接的有限元仿真[J]. 機械設(shè)計與制造,2009(7)：42-44.

[5]周星, 高學仕, 李文勇. 雙級套管螺紋連接有限元分析[J]. 管道技術(shù)與設(shè)備, 2009(5): 31-32.

[6]何平, 劉光復(fù), 谷葉水, 等. 基于三維精確建模法的螺栓有限元分析[J]. 中國機械工程, 2012, 23(16): 1991-1996.[7]呂端, 曾東建, 于曉洋, 等. 基于ANSYS Workbench的V8發(fā)動機曲軸有限元模態(tài)分析[J]. 機械設(shè)計與制造，2012(8)：11-13.

[8]周海超，左言言，鮑林曉．四缸柴油機曲軸的自由模態(tài)分析[J]. 噪聲與振動控制, 2010(6): 63-64.

[9]李松波, 馬星國, 韓輝．發(fā)動機曲軸的模態(tài)分析[J]. 沈陽工業(yè)學院學報,2003，22(4)：72-74.

The finite element strength analysis of the ballpoint pen tip in automatic assembly

LI Heng, LI Zheng-jun, HU Ding, YANG Lei

(Institute of Oceanographic Instrumentation,Shandong Academy of Sciences，Qingdao 26600, China)

∶In view of the ballpoint pen tip fracture damages emerged during the assembly process of certain type of ballpoint pen equipment, 3D model of the ballpoint pen tip and the corresponding assembly equipment was constructed by Pro/Engineer,and process stress was analyzed by means of finite element analysis software ANSYS.The forces and failure patterns during various stages of assembly were acquired by means of data collect system, then the process stress was analyzed by means of finite element analysis software ANSYS,finding the maximum stress and stress concentration position.Furthermore,the related experiment was carried out to demonstrate the validity of the finite element analysis,then the reasons for damage of ballpoint pen head were found out, finally feasible solutions were put forward.

∶ballpoint pen; threaded connection; stress research; finite element analysis; solutions

10.3976/j.issn.1002-4026.2017.03.010

2017-01-13

海洋公益性行業(yè)科研專項(201505031)；山東省自然科學基金(ZR2015YL020)；山東省科學院青年基金(2014QN036，2015QN028)；青島創(chuàng)業(yè)創(chuàng)新領(lǐng)軍人才計劃(13-CX-24)

李恒(1988—)，男，碩士，研究方向為海洋儀器儀表。

TH122

A

1002-4026(2017)03-0051-07