數形結合思想在高中數學教學中的應用

韓玉紅

摘要：數形結合思想貫穿著整個高中數學內容的始終，同時它在高考中占有非常重要的地位。所謂數形結合思想，就是在研究問題時把數和形結合起來考慮。通過“以形助數，以數解形”，能夠使復雜問題簡單化，抽象問題具體化。在應用數形結合思想方法的同時注意遵循等價性原則、雙向性原則、簡單性原則。

關鍵詞：數形結合思想方法 數學解題 應用策略

一、引言

數學思想是數學的靈魂，是數學知識的高度概括，是學生解決問題的手段。最常用的數學思想有函數與方程思想、轉化與化歸思想、分類討論思想、數形結合思想。其中，數形結合思想在數學中的地位尤為重要，是數學思想方法的精髓之一。我國著名數學家華羅庚先生在1964年1月撰寫的《談談與蜂巢的結構有關的數學問題》用一首詩完美的闡述了數形結合的價值和本質，即“數形本是相倚依，焉能分作兩邊飛。數缺形時少直覺，形缺數時難入微。數形結合百般好，隔裂分家萬事休。幾何代數統一體，永遠聯系莫分離。”

數形結合思想的應用十分廣泛，運用數形結合思想可以解決高中數學中的與集合、函數、方程與不等式、三角函數、向量、線性規劃、數列、解析幾何、立體幾何等有關的問題。縱觀歷年高考題，數形結合思想在歷年高考題中的體現逐漸加強。高中數學教學應該培養學生數形結合的解題思想，使學生在解題時有效的運用數形結合思想，做到舉一反三、觸類旁通。

二、數形結合方法的應用原則

數形結合的思想方法中數與形相互轉化時，要借助于基本的知識和方法才能實現，如果對基本知識和方法了解不深刻，就會容易犯錯。高中數學教學應用數形結合思想方法需要掌握以下原則。

1.等價性原則

在數形結合的過程中，數和形的轉化要遵循等價原則，即數和形所反應的對應關系是一一對應的。注意轉化過程要等價，避免定義域擴大或縮小。在畫圖時，注意對交點，極大（小）值點，最大（小）值點，數軸等的精確描繪。

2.雙向性原則

在運用數形結合思想解題時，進行幾何直觀分析時應該與代數計算相結合，“以形助數，以數解形”，用直觀的幾何反應抽象的公式，用精確的代數規范幾何圖形。

3.簡單性原則

“以形助數”進行由數到形的轉換時，應盡可能使構造的圖形簡單、易懂。“以數解形”在代數計算中盡量避免繁瑣復雜的計算。

三、數形結合思想解決的問題

數形結合思想是高中數學教學中解題的主要方法之一，下面是利用該方法可以解決的高中數學問題。

（1）解決集合問題。在關于集合之間的關系和運算的教學中，使用Venn圖是重要的，有助于學生學習、掌握、運用集合語言和其他數學語言。

（2）解決函數問題。函數是描述變量之間的依賴關系的重要數學模型。要求掌握幾種不同增長的函數模型（指數函數、對數函數、冪函數、反函數等），另外，數形結合還可以解決函數和方程的解的問題。

（3）解決方程與不等式問題。處理方程問題時，把方程的根的問題看作兩個函數的交點問題；處理不等式時，從題目的條件和結論出發，聯系相關函數，著重分析其幾何意義，從圖形上找出解題的思路。

（4）解決三角函數問題。單位圓是研究三角函數的重要工具，借助它的直觀，可以使學生更好地理解三角函數的概念和性質，體現了數形結合的思想。

（5）解決線性規劃問題。線性規劃問題是在約束條件下求目標函數的最值的問題，在解題時注意運用數形結合思想。

（6）解決數列問題。數列是一種特殊的函數，數列的通項公式和前n項和的公式可以看作關于正整數n的函數，借助函數圖像對數列進行直觀分析。

（7）解決解析幾何問題。解析幾何的本質是用代數方法研究圖形的幾何性質。解析幾何的研究對象是幾何圖形（平面解析幾何研究的是曲線），研究方法是用代數方法研究幾何解析幾何所要解決的主要問題有兩個：一是根據結合幾何性質求出曲線的方程，這體現了幾何向代數的轉化；二是根據方程研究曲線，這體現了由代數向幾何的轉化。

（8）解決立體幾何問題。教師可以使用具體的長方形的點、線、面之間的關系作為載體，使學生在直觀感知的基礎上認識空間中的一般的點、線、面之間的位置關系，通過對圖形的觀察、實驗和說理，使學生進一步了解平行、垂直關系的基本性質和判定方法。立體幾何中用坐標的方法將點、線、面的性質和相互關系的問題轉化為純粹的代數問題。

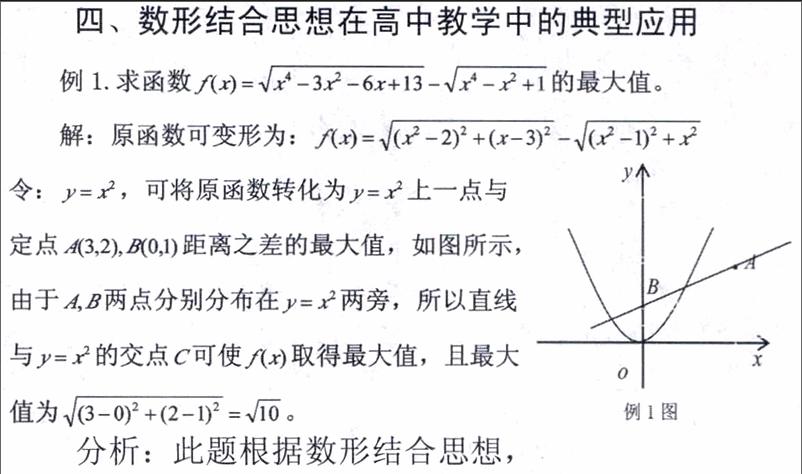
四、數形結合思想在高中教學中的典型應用

分析：此題根據數形結合思想，講求函數的值域問題轉化為

幾何圖形問題，把利用幾何圖形的性質把結論還原到函數問題。

此題最關鍵的是對函數的轉化，如果學生對距離公式有比較深刻的認識，那么就能夠解出這種類型的題。

分析：單位圓是表示三角函數的重要依托，本題將分式轉化為斜率，使解題過程清晰、簡明。此外，以后解題時遇到平方和式可轉化為距離，分式可轉化為斜率。

分析：通過已知，在坐標上畫圖，在解題時設的未知量在圖像中用輔助線表示出來，再將所得的未知點帶入方程中，求得結果即可，體現了數形結合的思想。向量具有兩個明顯的特點—“形”的特點和“數”的特點，這就使得向量成了數形結合的橋梁，向量的坐標實際是把點和數聯系了起來，進而可把曲線與方程聯系起來。這樣就可以用代數方程研究幾何問題，同時也可以用幾何的觀點處理某些代數問題，在教學中注意這種思想方法的運用。

五、結語

綜上所述，數形結合思想應用十分廣泛。在解題時對于某些較復雜的問題，可以運用數形結合思想將復雜的問題轉化為簡單的問題求解，大大簡化了解題過程，尤其在選擇題和填空題中更有其優越性。因此，在日常的教學中，教師要注意培養學生應用數形結合思想的意識，靈活運用數形結合，提高解題能力。

參考文獻：

[1]徐漢文.中學數學課程標準與教材分析.北京：科技出版社，2014.

[2]顧亞萍.數形結合思想方法之教學研究[D].南京師范大學，2004.

[3]劉紅艷.高中生運用數形結合思想解題的調查研究[D].南京師范大學，2014.

[4]李雪川.高中數學數形結合思想的研究和應用[D].河北師范大學，2013.