基于ANSYS優化技術的非對稱管板的分析與設計

孫偉明，石秀真，周 文，常 波，李劍虹

(1.浙江工業大學 化工機械設計研究所，浙江 杭州 310014；2.衢州市特種設備檢驗中心，浙江 衢州 324000)

基于ANSYS優化技術的非對稱管板的分析與設計

孫偉明1，石秀真1，周 文2，常 波1，李劍虹1

(1.浙江工業大學 化工機械設計研究所，浙江 杭州 310014；2.衢州市特種設備檢驗中心，浙江 衢州 324000)

非對稱管殼式蒸發器是低溫余熱發電的核心設備，在近年來應用越來越廣泛.非對稱管板即管板的管束布置呈非對稱狀，而管束的特殊分布使得管板的應力情況復雜，目前沒有非對稱管板板厚的具體計算公式，只能借助數值求解的方法來計算.從安全生產的角度出發，為了在滿足結構強度的要求下達到成本最小的目的，利用ANSYA有限元軟件對構件進行了應力分析，通過ANSYS優化技術，選取管板厚度為設計變量，蒸發器質量為目標函數，對管板參數進行優化，最終得出了合理的結果.

非對稱管板；有限元；優化設計

膨脹機蒸發器是一種有特殊用途的管殼式換熱器，應用于石油相關的氣體加工、能量回收、蒸汽與各種氣體的減壓等場合[1].膨脹機蒸發器在設計時為給殼程一個氣相膨脹空間，設計成上下非對稱管板，換熱管布置在管板下半部分.由于蒸發器管板的形狀和受力復雜，所以在結構設計時不能依據常規設計標準熱交換器GB/T 151—2014[2].隨著有限元分析技術的出現，人們越來越多地將這種技術應用于非對稱管殼式換熱器的管板結構設計.有限元設計方法能滿足結構強度的要求，但不一定是結構設計中的最優方法[3-10].有限元計算和優化方案相結合，是尋找最優方案的一種有效方法.利用ANSYS提供的參數優化功能，提出了非對稱式管殼式換熱器管板的優化設計的方法.

1 蒸發器結構和參數

蒸發器為固定管板式換熱器，管板下半部分的換熱管采用對稱式布置，共有換熱管1 850根，管長9 000 mm，換熱管與管板之間采用脹接方式連接，其管板結構如圖1所示.

這里重點研究的是蒸發器的管板，管板初始厚度為79 mm，假設為平蓋厚度按照壓力容器GB 150—2011[11]確定.管板的主要性能參數如表1所示.

表1 管板主要參數

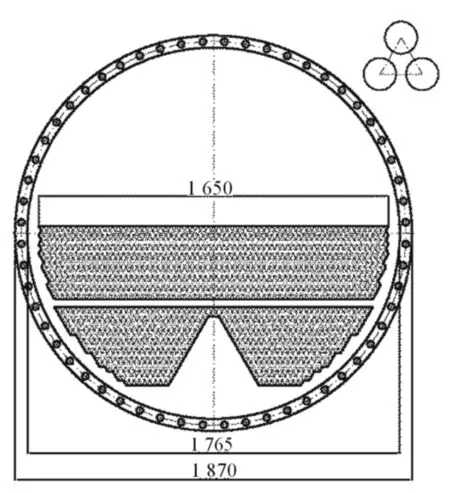
圖1 管板結構及布管方式Fig.1 The tube sheet and piping manner

2 有限元分析

2.1 有限元模型

如圖1所示，蒸發器為左右對稱結構，為了減少計算的量，建模時取其1/2對稱模型.由于本次計算主要是針對管板的厚度，在計算過程中只考慮與管板有關的法蘭、殼體和換熱管而忽略了殼體內部的其他非承壓部件.模型采用solid186單元對模型進行網格劃分.模型中，共有384 780個單元，609 524個節點，其模型如圖2所示.

圖2 有限元模型圖Fig.2 Finite element model

2.2 約束和載荷

管板在工作中承受管程壓力、殼程壓力、墊片壓緊力和螺栓預緊力的作用.其中管程壓力和殼程壓力為已知條件，墊片壓緊力和螺栓預緊力根據GB 150—2011進行計算，計算公式為

Fp=6.28DGbmpc

(1)

(2)

式中：Fp為墊片壓緊力，N；DG為墊片壓緊力作用中心圓直徑，mm；b為墊片有效密封寬度，mm；m為墊片系數；pc為計算壓力，MPa；Wp為螺栓預緊力，N.蒸發器中共有螺栓56個，通過計算得到墊片壓緊力為4.92N，單個螺栓的預緊力為13 338N.

從工作參數可以看到蒸發器的殼程設計溫度為144 ℃，管程設計溫度為150 ℃，由于法蘭、管板、殼體和換熱管的溫度在144～150 ℃范圍內，溫差較小，可以忽略不計，本次有限元分析過程中未考慮溫度場對管板的影響.

2.3 結果分析

根據設計條件，對蒸發器管板在管程與殼程同時承受壓力、管程單獨受壓以及殼程單獨受壓等三種情況下進行應力計算分析，得到管板最大應力位置處應力情況如表2所示.由表2可知：當殼程單獨受壓時，產生的Stressintensity應力強度、一次薄膜應力值和彎曲應力值等皆大于管程單獨受壓、管程與殼程同時承受壓力時的應力值，所以，以下優化計算中以殼程單獨受壓為準.

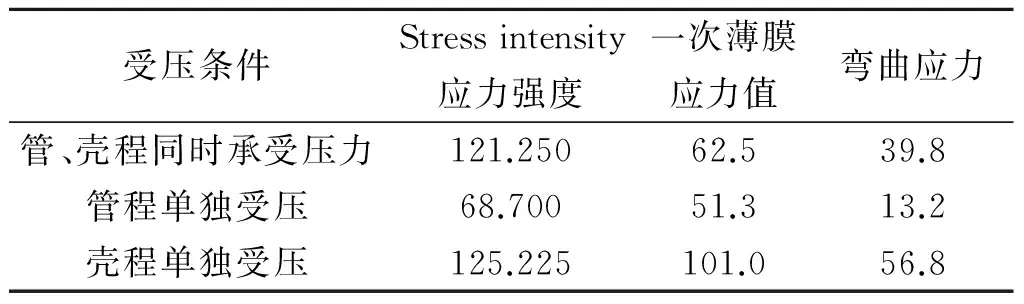
表2 管板應力

從上述計算結果可以看出：三種加載情況下最大應力值都出現在管板與筒體連接的焊縫上，如圖3(a)所示.根據平板的受力情況可知，筒體內應力均勻分布，最大應力出現在管板與筒體連接處.而均勻布管管板，由管板彎矩分布及彎曲應力分布情況得出，管板最大徑向彎矩及彎曲應力出現在布管區邊界位置.而非對稱管板布管在下半部分，管板上半部分為平板，管板承受內壓，布管區有換熱管支撐，所以最大應力發生在上半部分，又焊縫處應力集中，所以非對稱管板應力分布介于平板和均勻布管管板之間.

1—焊縫/最大應力位置；2—管板中心；3—邊緣；4—布管邊界圖3 管板應力分布云圖Fig.3 Stress contour plot of tube sheet

管板的安全分析不只取決于最大應力值發生位置，由JB/T 4732—2005[12]可知：平板的危險位置有板邊緣處、板中心處以及板與筒體連接處，而均勻布管管板需要進行應力校核的地方有管板中心、管板布管區與非布管區邊界處以及管板邊緣處.因為非對稱管板的特殊性，結合平板與管板，對其板中心、布管區與非布管區邊界處、管板與筒體連接的焊縫上以及邊緣處等進行應力分析.表3為對各處的應力進行分類得出的結果.

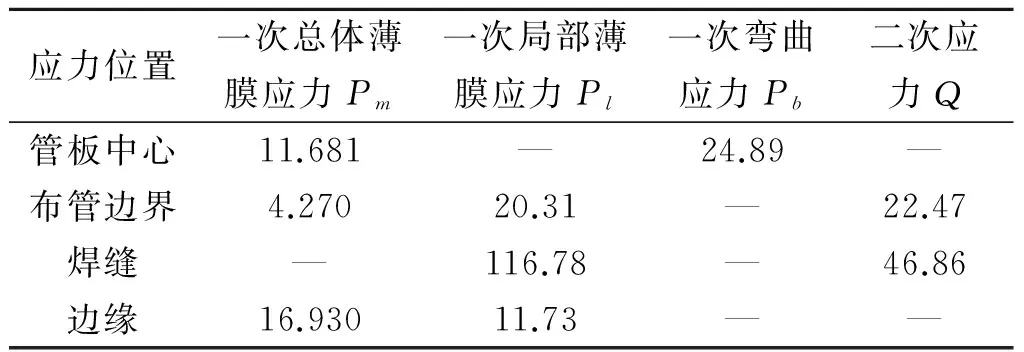
表3 各危險界面應力分類

2.4 對比分析

目前，對于非對稱管板的厚度計算以及應力校核都沒有具體公式，所以針對這類管板的設計與應力校核都存在一定困難.由上文可知：此類管板的應力分布介于平板與均勻布管管板，在此根據JB/T 4732—2005計算平板邊緣處、板中心處以及板與筒體連接處的最大應力強度，根據GB/T 151—2014計算均勻布管管板中心、管板布管區與非布管區邊界處以及管板邊緣處的最大應力強度.

表4為通過JB/T 4732—2005，GB/T 151—2014中的公式對平板及均勻布管管板的邊緣、中心、板與筒體連接處以及布管區與非布管區邊界處等危險界面進行應力計算得出的結果，與表3中非對稱管板的應力強度進行對比.

由上述對比結果可知：非對稱管板的最大應力粗略校核可參考相同工況下的平板與管板.具體危險界面的參考如下：管板中心及布管邊界可參考相同工況下的均勻布管管板，焊縫處及管板邊緣可參考相同工況下的平板.

表4 平板與管板各危險界面的應力

2.5 基于ANSYS進行優化

由上述分析可知：最危險的位置位于管板與筒體連接的焊縫上，以下優化部分則針對此位置進行.

管板與筒體的焊縫上，存在一次應力和二次應力.JB/T 4732—2005中有關應力強度的許用極限的規定：一次薄膜應力加一次彎曲應力小于等于1.5倍許用應力，一次應力加二次應力小于等于3倍許用應力.而GB/T 151—2014中規定，僅殼程壓力作用，不計膨脹差時，最大應力強度應小于1.5倍許用應力；計入膨脹差時，最大應力強度應小于3倍許用應力.本次計算中，忽略熱膨脹，綜合考慮JB/T 4732—2005和GB/T 151—2014，選取最大應力強度σmax<1.5[σ]，一次薄膜應力與彎曲應力的和σn<1.5[σ].由計算結果可知σmax=125.225 MPa.在最大應力發生位置進行應力分類，σn=157.8 MPa.σn，σmax都遠小于材料的1.5[σ]=250 MPa，雖然滿足了安全要求，但是材料利用率太小，導致經濟成本升高.

優化設計是一種尋找最優設計方案的設計方法，而最優設計方案是既能夠滿足所有設計要求的方案，又能保證支出(如體積、重量和費用等)最小，是最有效率的方案.ANSYS有限元軟件提供了適用于優化分析的一階優化方法[13].

由于優化計算是針對管板強度的安全設計，所以在保證安全的情況下，是以確定用材最少的設計方案為計算目的的.因此，除板厚之外其他尺寸不得改變.為使結構能滿足設計要求，選擇Stress intensity應力強度為狀態變量，確定管板厚度為設計變量.因為材料密度為常數，尋找滿足安全要求的最小管板厚度，同時也是構件的最小質量，因此可以選擇構件的質量作為目標函數.狀態變量為，假設管板厚度為T，變化范圍為20～100 mm，那么該問題的數學模型[14]可表示為

設計變量：T

目標函數：minWT(x)

當20 mm

按照優化過程的步驟，以原有計算模型為基礎，根據上述優化數學模型，采用參數化設計語言[15]，由ANSYS軟件的一階優化方法進行運算，在第8個循環步結束時得到了最優結果，計算終止.表5給出了每個循環步的計算結果，從表5中的數據可以看出：蒸發器非對稱管板經ANSYS軟件優化，最大應力強度已經從125.225 MPa升高到了250.99 MPa，管板厚度變為43.594 mm，對比初始值79 mm降低了43%，構件質量從2 630.8 kg降低到了2 325.5 kg，且滿足安全要求，大大提高了材料的利用率，降低了產品成本.因此最終優化結果應選擇表5中第8步的計算結果.

表5 優化數據的變化情況

注：1) 第8步為最優設計.

對設計變量優化結果T進行圓整，為方便加工，取管板厚度T=45 mm.修改計算模型，重新計算，得到管板應力云圖，其中最大應力強度σmax=249.30 MPa，一次薄膜應力加一次彎曲應力σn=204.43 MPa，構件應力強度云圖如圖3(b)所示.由圖3(b)看出：管板厚度發生變化后，最大應力位置沒有改變，且對比其他危險截面，焊縫處應力明顯大于其他危險截面，故在對管板進行優化設計時，僅考慮焊縫處.

根據GB/T 151—2014規定，對帶法蘭的管板的厚度進行設計時，不僅要保證管板的強度，也要保證管板的剛度以及換熱管的軸向應力σt，根據GB 150—2011，帶法蘭管板剛度指數J及換熱管軸向應力的計算式分別為

(3)

(4)

式中：VI為整體法蘭系數；M0為法蘭設計力矩，N·mm；λ為系數；δ0位法蘭有效厚度，mm；KI為剛度系數，取0.3；h0為參數；a為1根換熱管管壁金屬的橫截面積，mm2；d為換熱管外徑，mm；σt為換熱管軸向應力，MPa；[σ]t為設計溫度下換熱管材料的許用應力，MPa.換熱管選用材料為20號鋼，外徑為19 mm，壁厚為2 mm.

通過式(3，4)計算得出管板剛度指數J=6.72×10-5<1，軸向應力|σt|=2.92 MPa<[σ]t=147 MPa.計算結果滿足標準要求，可以保證管板優化后的結構安全.

3 結 論

借助ANSYS有限元分析軟件對蒸發器非對稱管板進行應力校核，并提供了一種簡略的校核方法.利用有限元優化模塊，在滿足強度要求的前提下建立數學模型，對管板的結構參數進行優化，可得出最優設計方案.利用ANSYS有限元優化技術求解結構優化問題，最突出的優點就是可避免煩瑣的建模、計算工作，從而可以提高設計效率，同時也滿足了機械設計中安全性、經濟性的需要.

[1] 陸征,蔣國.螺桿膨脹機的發展及應用[C]//2010年設備、機泵、攪拌年會會刊.大連：全國化工設備設計技術中心，2010.

[2] 中國國家標準化管理委員會.熱交換器: GB/T 151—2014[S].北京：中國標準出版社，2015:2.

[3] 徐學真,黃建冰,孫偉明.帶金屬O型環法蘭的密封性能有限元分析[J].浙江工業大學學報,2014,42(6):686-689.

[4] 劉天豐,陳建良,林興華.非對稱管殼式換熱器的三維有限元結構分析[J].壓力容器,2009(8):27-31.

[5] LIU Jingcheng, ZHANG Shuyou, ZHAO Xinyue, et al. Influence of fin arrangement on fluid flow and heat transfer in the inlet of a plate-fin heat exchanger[J]. Journal of zhejiang university science a,2015,16(4):279-294.

[6] 劉天豐.非對稱管殼式換熱器結構分析及改進中的問題研究[D].杭州:浙江大學,2005.

[7] 祝鈴鈺,姜波,任奕丞.基于集合算法的復雜精餾建模與求解[J].浙江工業大學學報,2014,42(2):152-156.

[8] 譚蔚,楊星,楊向濤.高參數換熱器管板熱應力分析模型的研究[J].壓力容器,2011,28(2):44-50.

[9] 徐璋,霍玉雷,陳勇,等.新型組合式垂直軸風機的優化設計與性能研究[J].浙江工業大學學報,2015,43(3):261-264.

[10] 郭奇凡.非對稱管殼式換熱器結構分析及改進中的問題研究[J].中國化工貿易,2013(4):90-90.

[11] 中國國家標準化管理委員會.壓力容器:GB 150.1-150.4—2011[S].北京：中國標準出版社,2011.

[12] 原全國壓力容器標準化技術委員會(SAC/TC 262).鋼制壓力容器—分析設計標準:JB/T 4732—2005[S].北京：中國標準出版社,2005.

[13] 王金龍,王清明,王偉章.ANSYS12.0有限元分析與范例解析[M].北京:機械工業出版社,2010：203-241.

[14] 陳水生,屠立群,孫偉明.基于ANSYS優化技術的不等截面塔連接部位強度設計[J].化工裝備技術,2006(4):56-59.

[15] 龔曙光,謝桂蘭,黃云清.ANSYS操作命令與參數化編程[M].北京:機械工業出版社,2004：343-355.

(責任編輯：陳石平)

Strength analysis and design of asymmetric tube sheet based on ANSYS optimization techniques

SUN Weiming1, SHI Xiuzhen1, ZHOU Wen2, CHANG Bo1, LI Jianhong1

(1.Institute of Process Equipment and Control Engineering, Zhejiang University of Technology, Hangzhou 310014, China；2.Quzhou Special Equipment Inspection Center, Quzhou 324000, China)

Unsymmetrical shell and tube evaporator is the core equipment, and it is used in the low temperature waste heat power generation process in recent years. Because of the tube bundle is asymmetric so the stress of the unsymmetrical tube sheet is very complicated, and there is no specific formula to calculate the thickness of the unsymmetrical tube sheet. From the safety purpose and the minimum cost, the tube sheet thickness is selected as design variable, component quality is selected as objective function. The stress of tube sheet is analyzed by ANSYS finite element method, and the thickness of the tube sheet is optimized and the reasonable result is got finally.

unsymmetrical tube sheet; finite element method; design optimization

2016-11-06

國家質量監督檢驗檢疫總局科技計劃項目(2014QK195)

孫偉明(1964—)，男，浙江杭州人，教授，博士，研究方向為過程裝備的結構完整性技術，E-mail：wmsun@zjut.edu.cn.

TB653

A

1006-4303(2017)04-0366-04