二階互補濾波姿態求解器的設計

南余榮,宛冬晴,潘 帥,姚亞楠

(浙江工業大學 信息工程學院，浙江 杭州 310023)

二階互補濾波姿態求解器的設計

南余榮,宛冬晴,潘 帥,姚亞楠

(浙江工業大學 信息工程學院，浙江 杭州 310023)

為了降低小型四旋翼姿態解算的成本和提高姿態輸出精度，采用了低成本MPU-9250作為IMU，設計了一種二階互補濾波姿態求解器.二階互補濾波算法所產生的計算量不大并且對處理芯片的性能要求不高，從而達到降低成本的目的.通過實際測試,以成品AHRS100作為航姿參考系統，得出姿態角度動態誤差在3°以內.實驗結果表明：所設計的姿態求解器能較精確地解算出四旋翼的姿態角度，滿足了小型四旋翼對輸出姿態精度的要求.

四旋翼；二階互補濾波；姿態角度

隨著科技的進步和時代的發展，無人機憑借自身特有的優勢，在民用軍事和農業中得到了廣泛的應用[1]，例如可以用無人機進行航拍攝影，電力巡檢，新聞報告，噴灑農藥，偵查敵情，還可以用無人機來送快遞，在這些方面無人機有著人工所不具備的特有優勢，無人機成為當下科技行業研究的熱點.一直以來，在諸多研究問題中，飛行器的姿態解算問題都是研究的重點[2-3].在小型四旋翼姿態解算中一般采用低成本捷聯慣性導航測量單元，主要由陀螺儀，磁力計和加速度計組成，陀螺儀具有很好的動態跟蹤特性[4-5]，在飛行器飛行過程中測得的角速度會比較準確，實際上單獨用陀螺儀也能解算出四旋翼的姿態，但是由陀螺儀測量得到的積分角度會產生誤差的累積，如果不加以補償，長時間可能引起嚴重的偏差，所以筆者利用加速度計和磁力計對陀螺儀解算的角度進行誤差補償[6-7].

計算四旋翼在三維空間的旋轉有很多種等價的表示方法，常見的有方向余弦、四元數和歐拉角[8].歐拉角雖然簡單易于表示和理解，但是由于其自身的姿態表示特點導致萬向節死鎖，不能全方位地解算出四旋翼的姿態方位，方向余弦法雖然能滿足四旋翼全方位姿態解算的要求，但是需要的運算量太大[9-10]，在采用低成本處理芯片的平臺中，導致姿態不能實時輸出.故筆者采用四元數來表示姿態變化，四元數有一些其他角位移表示方法所沒有的優點如平滑插值，能和矩陣形式快速轉換等[11-12].融合加速度計，陀螺儀和磁力計測得數據的方法有一階互補濾波，二階互補濾波和擴展卡爾曼濾波等[13]，擴展卡爾曼算法雖然比較先進，解算出來的角度能很好地跟蹤飛行器真實的角度，但其設計復雜，計算量大，在小型四旋翼中普遍使用的低成本慣性測量單元不滿足其對IMU性能的要求[14].一階互補濾波算法雖然設計簡單，易于調試，只需調節一個參數，但解算精確度差.故筆者采用了二階互補濾波算法，以STM32F103C8T6為CPU，IMU采用MPU-9250，這兩個模塊累計成本在30元左右，而卡爾曼濾波算法采用的CPU和IMU模塊累計成本普遍在80～120元之間，加入PI環節補償單獨用陀螺儀測量所產生的誤差，通過調節兩個參數KP和Ki最終解算出了較精確的姿態[15-16]，滿足了小型低成本四旋翼飛行器求解姿態過程中對成本和精度的綜合要求.

1 系統建模

對四旋翼進行姿態解算前首先要建立導航坐標系n系和機體坐標系b系，建立的導航坐標系坐標原點位于四旋翼的質心，xn軸指向北，yn指向東，zn指向地即東北地坐標系，三條軸之間都是倆倆垂直的，同理建立四旋翼的機體坐標系，機體坐標系和四旋翼固聯，隨著四旋翼的旋轉而旋轉，坐標系如圖1所示.

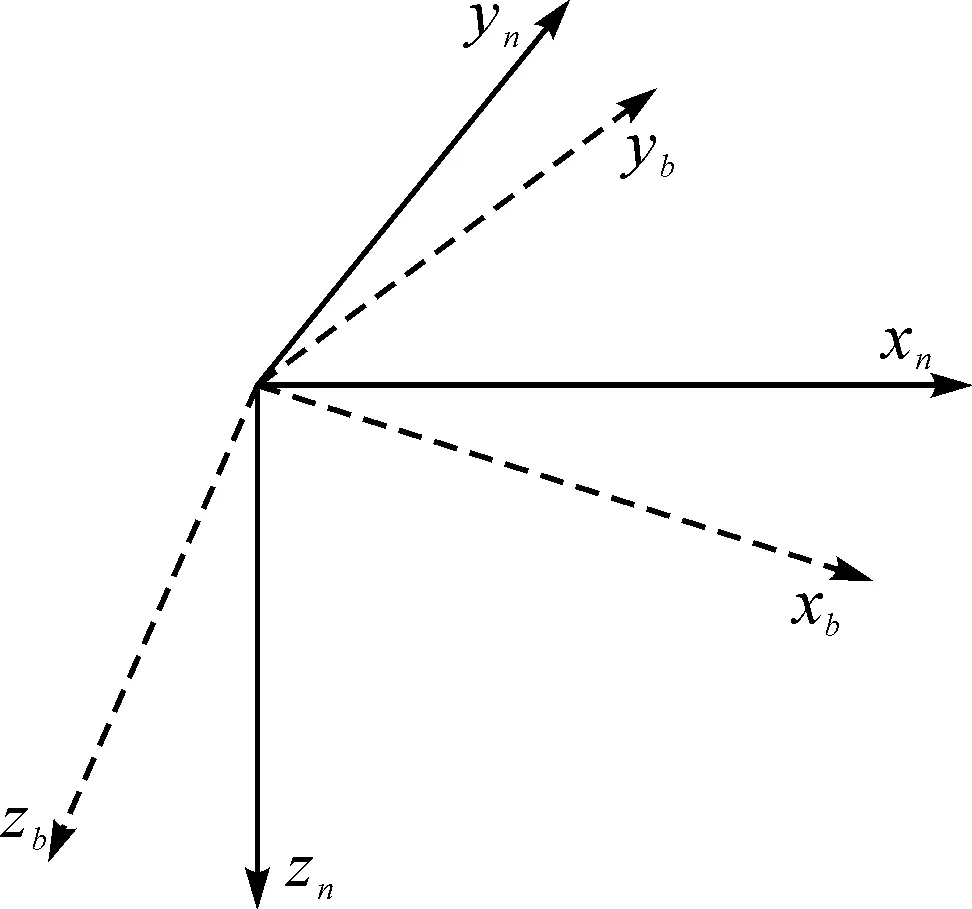
圖1 機體坐標系和導航坐標系Fig.1 Body axes coordinate system and navigation coordination system

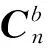
(1)

四元數是一種高階復數，能很方便地刻畫飛行器繞任意軸的旋轉，且計算量小.四元數q的表達式為

(2)

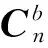
(3)

2 二階互補濾波算法設計和姿態解算過程

陀螺儀動態響應好，積分后可測傾角，但在解算姿態的過程中，會產生累積誤差和零漂等，在低頻段信號不好.磁力計和加速度在低頻段表現優秀，但是瞬時特性很差，當四旋翼姿態劇烈變化時，不能滿足四旋翼實時解算的要求.因此可以結合它們分別在高頻段和低頻段的優勢，利用互補濾波原理對陀螺儀測得的姿態角度進行高通濾波，對磁力計和加速度計測得的姿態角度進行低通濾波，得到在高頻段和低頻段都較好的信號，濾波原理如圖2所示.

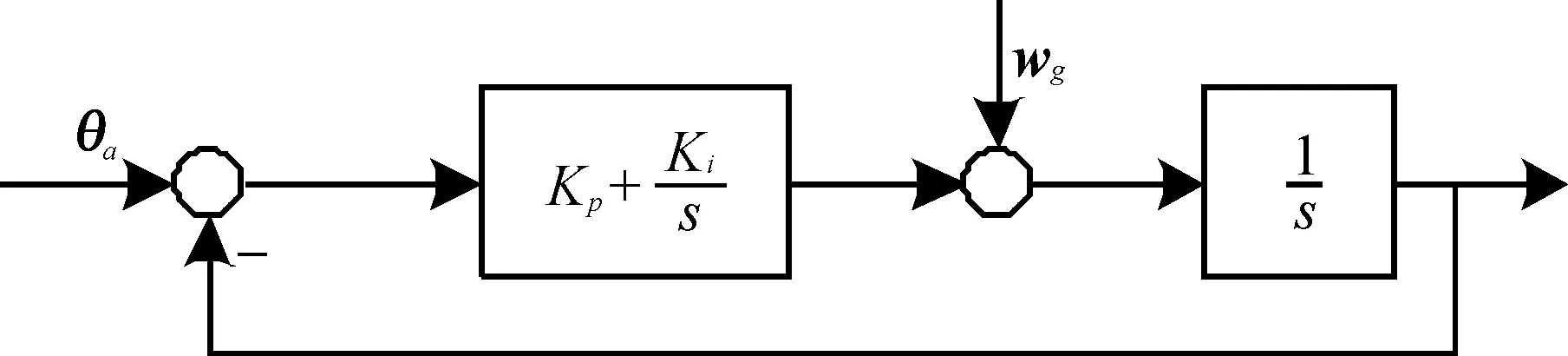
圖2 二階互補濾波原理Fig.2 The principle of second order complementary filter algorithm

由圖(2)可以進一步得到二階互補濾波公式為

(4)

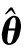
(5)

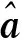
(6)

總的誤差向量e為

(7)

式中：e1為加速度計測得的單位向量與從四元數那里獲得的重力向量之間的誤差向量；e2為磁力計測得的單位向量與從四元數那里得到的單位向量之間的誤差向量.令δ=(Kp+Ki/s)·e，陀螺儀測得的角速度為wg，將δ與wg進行疊加得到修正后的角速度w，最后來更新四元數，得

(8)

式中w=0+wxi+wyj+wzk，由式(8)可以得到四元數的迭代方程式為

(9)

由式(9)可知：只需傳入角速度在三個軸的分量和周期T即可求得下一周期的四元數值，將求得的四元數進行單位化，得到最終表示四旋翼姿態的歐拉角為

(10)

詳細的姿態解算過程，如圖3所示.

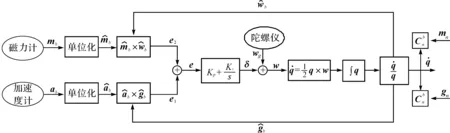
圖3 姿態解算過程Fig.3 The process of attitude calculation

3 實驗測試和結果分析

3.1 實驗平臺

我們選用STM32F103C8T6為CPU，IMU采用MPU-9250，MPU-9250是一個QFN封裝的復合芯片，它由兩部分組成，一組是3軸加速度計和3軸陀螺儀，另一組則是AKM公司的AK896 3軸磁力計.采用AHRS100成品航姿系統作為參考系統進行對比，AHRS100在各種惡劣條件下均能精確解算出四旋翼的姿態.

3.2 測試結果和分析

將一階互補濾波算法和二階互補濾波算法的廉價IMU單元與AHRS100固定在四旋翼上并在實際場景下飛行，通過計算機串口同時讀取3個測量單元的數據進行實時姿態解算，采樣時間為60s，以AHRS100成品航姿系統測得的姿態數據為參考標準進行MATLAB繪圖.圖4為一階互補濾波姿態求解器、二階互補濾波姿態求解器和參考航姿系統所測得的俯仰角輸出對比情況，進一步利用MATLAB內置的計算工具，求出俯仰角誤差，如圖5所示，可以很明顯看到大部分時間里一階解算角度誤差都是大于二階解算角度誤差，二階解算角度誤差第4s和第6s左右達到最大，接近2°.而一階解算角度最大誤差在第25s達到了3.2°.

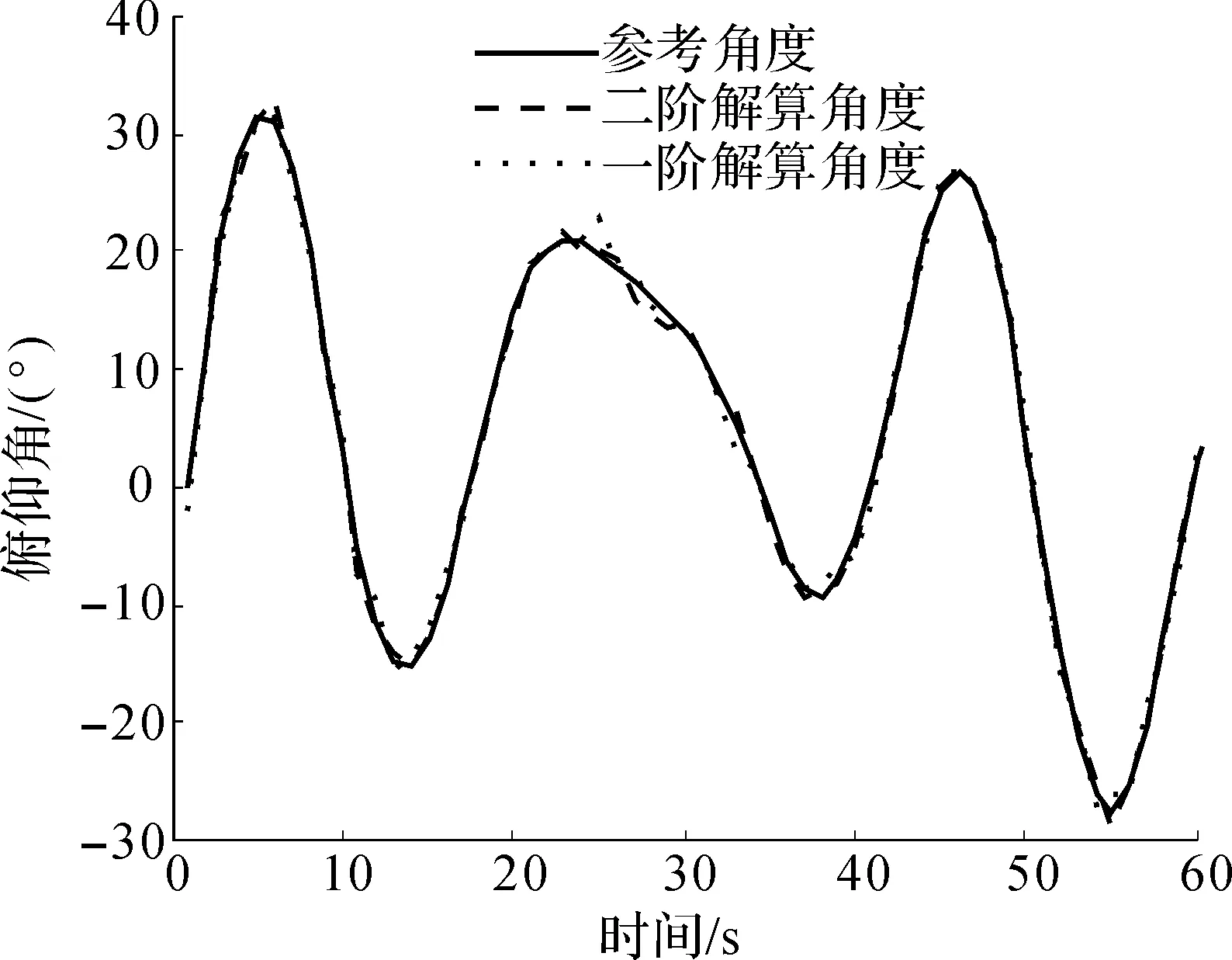
圖4 俯仰角對比情況Fig.4 Contrast of pitch angle

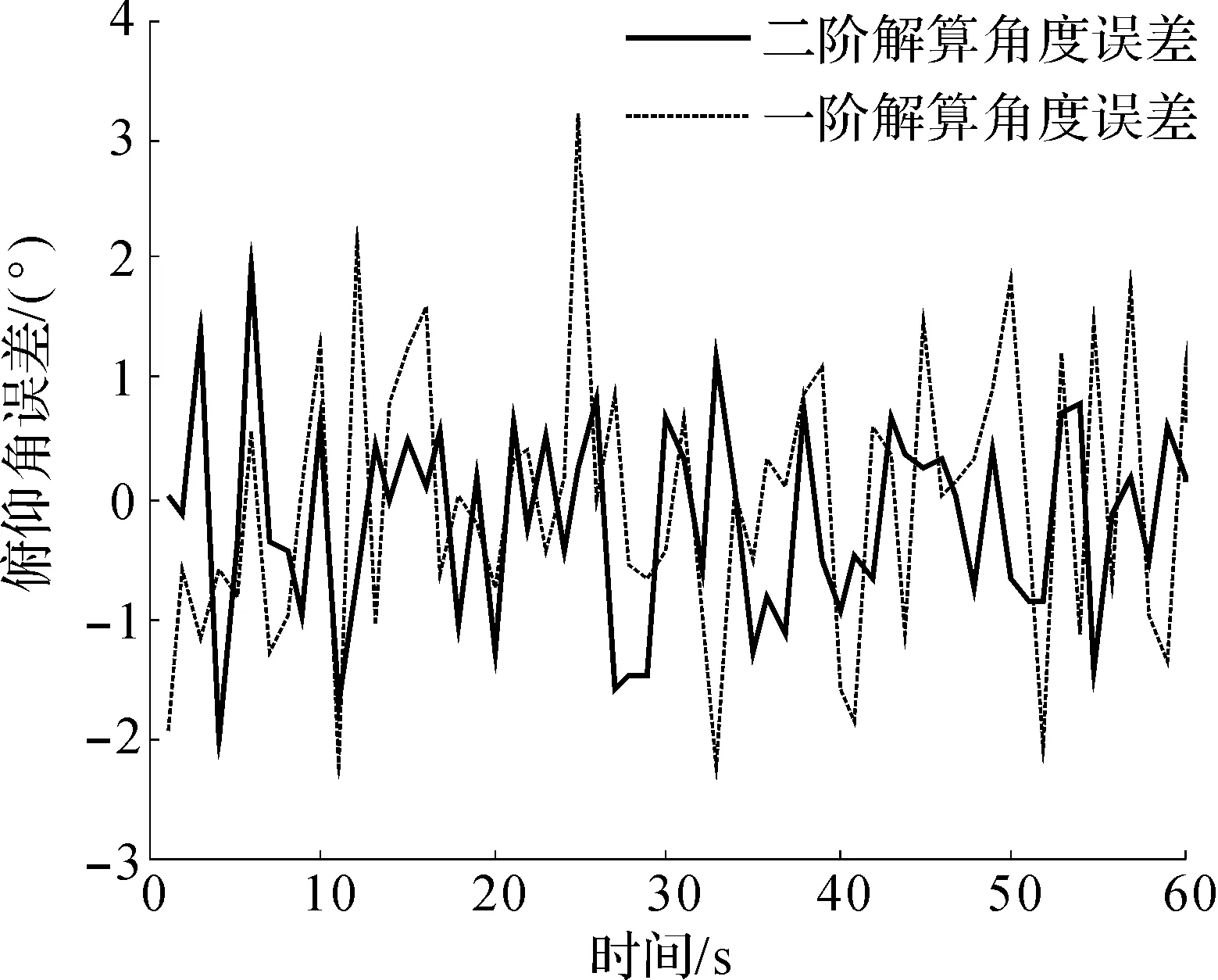
圖5 俯仰角誤差Fig.5 Error of pitch angle

圖6為測得的橫滾角輸出對比情況，進一步繪制出橫滾角誤差(圖7)，可以很明顯看到大部分時間里一階解算角度誤差都是大于二階解算角度誤差.在幾個特殊的時間點由于飛行器姿態變化劇烈導致姿態求解角度和真實角度偏差較大，在第18s左右二階解算角度誤差達到最大，達到2.3°.而一階解算角度最大誤差在第39s左右達到了4.3°.

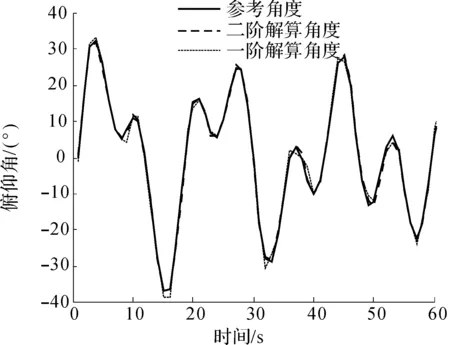
圖6 橫滾角對比情況Fig.6 Contrast of roll angle

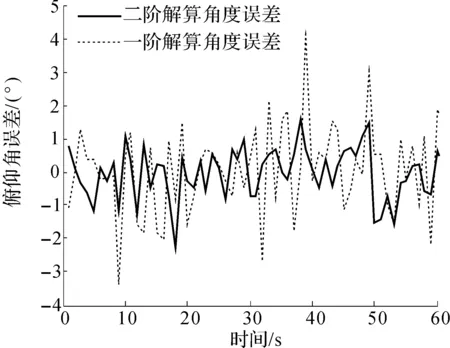
圖7 橫滾角誤差Fig.7 Error of roll angle

圖8為測得的偏航角輸出對比情況，進一步繪制出偏航角誤差，如圖9所示，可以很明顯看到大部分時間里一階解算角度誤差都是大于二階解算角度誤差.二階解算角度誤差大多在1.5°以內.而一階解算角度誤差在很多時刻都超過了1.5°，解算精度明顯低于二階解算精度.

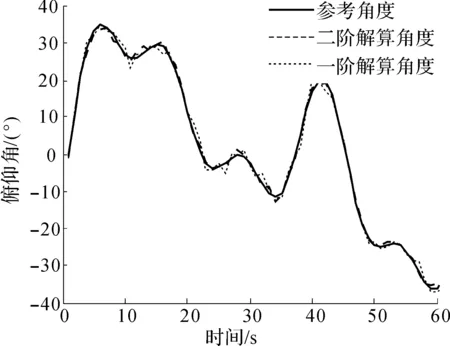
圖8 偏航角對比情況圖Fig.8 Contrast of yaw angle

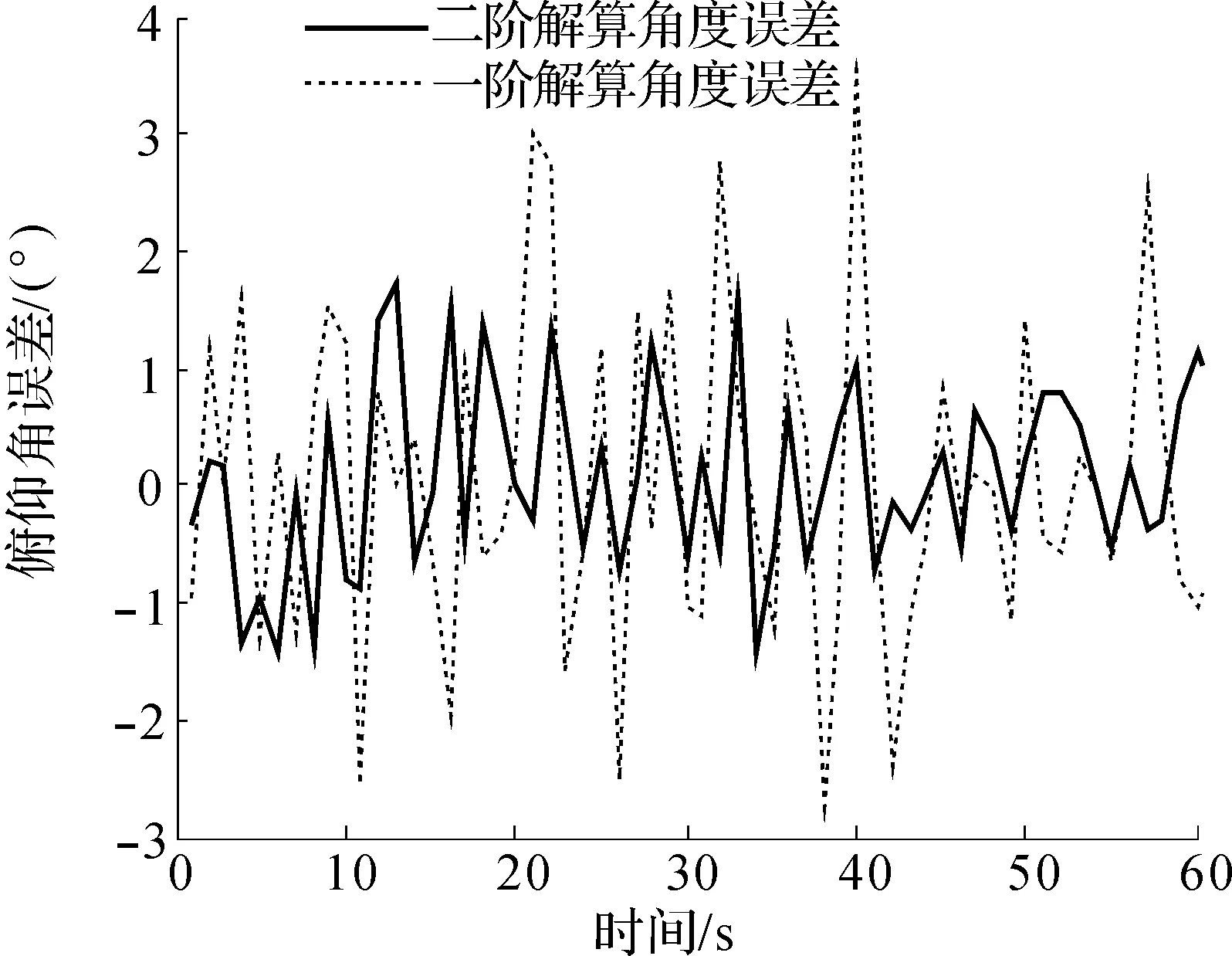
圖9 偏航角誤差Fig.9 Error of yaw angle

可以得到四旋翼在飛行過程中，無論是俯仰角，橫滾角還是偏航角，一階解算的精確度都是明顯低于二階解算的精確度.大多數時間內二階解算俯仰角誤差，橫滾角誤差和偏航角誤差分別控制在2°，1.5°，1.5°以內，姿態角最大動態誤差小于2.5°，滿足小型低成本四旋翼飛行器對輸出姿態精度的要求.

4 結 論

針對小型四旋翼姿態解算這一問題進行了詳細的分析，通過對比一階互補濾波算法，卡爾曼濾波算法，二階互補濾波算法最后設計了一種基于四元數的二階互補濾波姿態求解器，并對解算的原理和流程做了詳細介紹.以四旋翼飛行器為實驗平臺，通過實際飛行測試，對比二階互補濾波姿態求解器和一階互補濾波姿態求解器解算出的角度誤差，得出了二階解算精度明顯高于一階解算精度的結論，驗證了筆者所設計的二階互補濾波算法在提升輸出姿態精度上的有效性.

[1] 郭曉鴻，楊忠，陳喆，等.EKF和互補濾波在飛行姿態確定中的應用[J].傳感器與微系統，2011，30(11):56-58.

[2] 王立波.捷聯慣導系統設計與數據處理技術研究[M].北京：科學出版社，2006.

[3] 史智寧，韓波，徐玉，等.基于重力場自適應互補濾波的無人直升機水平姿態估計方法[J].傳感技術學報，2009，22(7):993-996.

[4] 方路平，高坤，潘清，等.基于陀螺儀的穿刺手術導航系統設計[J].浙江工業大學學報，2016，44(2)：129-133.

[5] 王宇，董輝，徐建明，等.一種新的智能小車控制策略[J].浙江工業大學學報，2012，40(2)：217-221.

[6] 胥芳，倪紫京，占紅武.自平衡小車的模型分析與數據處理[J].浙江工業大學學報，2016，44(3)：288-291.

[7] 張榮輝，賈宏光，陳濤，等.基于四元數法的捷聯慣性導航系統的姿態解算[J].光學精密工程.2008，16(10):1963-1970.

[8] 張承岫，李鐵鷹，王耀力.基于MPU6050和互補濾波的四旋翼飛控系統設計[J].傳感技術學報，2016，29(7)：1011-1015.

[9] 蔡磊，牛小驥，張提升，等.MEMS慣導在四旋翼飛行器中導航性能的實驗分析[J].傳感技術學報，2016，29(5)：711-715.

[10] 彭孝東，張鐵民，李繼宇，等.基于傳感器校正與融合的農用小型無人機姿態估計算法[J].自動化學報，2015，41(4)：854-860.

[11] 王延東，賈宏光.組合導航系統濾波器截斷誤差抑制方法[J].傳感技術學報，2014，27(5)：616-621.

[12] 鄭君里，楊為理，應啟珩.信號與系統[M].北京：高等教育出版社，2000.

[13] 文常保，高麗紅，方吉善，等.基于改進型限幅平均濾波法的高精度稱重系統研究[J].傳感技術學報，2014，27(5)：649-653.

[14] 張洪濤.四旋翼微型飛行器位姿及控制策略的研究[D].哈爾濱：哈爾濱工業大學，2014.

[15] 傅忠云，劉文波，孫金秋，等.自適應混合濾波算法在微型飛行器姿態估計中的應用[J].傳感技術學報，2014，27(5)：698-703.

[16] 彭孝東，張鐵民，李繼宇，等.基于傳感器校正與融合的農用小型無人機姿態估計算法[J].自動化學報，2015，41(4)：854-860.

(責任編輯：陳石平)

Design of second order complementary filter attitude solver

NAN Yurong, WAN Dongqing, PAN Shuai, YAO Yanan

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

A second order complementary filter solver is designed in order to reduce the cost and improve the output precision of small quad-rotors in attitude calculation process. The Low-cost MPU-9250 is adopted as IMU in this paper. The second-order complementary filtering algorithm produces little computation and the performance requirement of the processing chip isn’t high. It will achieve the purpose of reducing cost. Through the practical test, using AHRS100 as attitude reference system, and the dynamic error of the attitude angle is less than 3°. The experimental result show that the solver designed in this paper can calculate the attitude angle fairly accurately and meet the requirement of output precision of small quad-rotors.

quad-rotors; second order complementary filter; attitude angle

2016-11-30

浙江省自然科學基金資助項目(Z12E070003)

南余榮(1966—)，男，浙江樂清人，教授，博士，研究方向為電力傳動及其自動化，E-mail：nyr@zjut.edu.cn.

TP273

A

1006-4303(2017)04-0416-05