大長細比導彈的氣動彈性降階模型1)

楊執鈞 黃 銳 劉豪杰 趙永輝 胡海巖,2) 王 樂

?(南京航空航天大學機械結構力學及控制國家重點實驗室，南京210016)?(中國運載火箭技術研究院，北京100076)

大長細比導彈的氣動彈性降階模型1)

楊執鈞?黃 銳?劉豪杰?趙永輝?胡海巖?,2)王 樂?

?(南京航空航天大學機械結構力學及控制國家重點實驗室，南京210016)?(中國運載火箭技術研究院，北京100076)

對于大長細比導彈，需要在設計階段準確計算氣動彈性/氣動伺服彈性，但其復雜的氣動力給計算帶來困難，因此氣動力降階模型是突破大長細比導彈跨音速氣動彈性分析與控制瓶頸的關鍵技術.雖然氣動力模型降階方法已在預測二維機翼結構的氣動彈性方面取得重要進展，但幾乎未見關于全機模型的氣動力降階模型研究報道.本文基于遞歸Wiener模型的氣動力降階方法，利用CFD計算的氣動力作為模型辨識數據，用魯棒子空間和Levenberg-Marquardt算法辨識降階模型參數，建立了大長細比導彈氣動力降階模型.在此基礎上與大長細比導彈有限元模型相結合，構造出氣動彈性降階模型，并在數值仿真中測試氣動彈性降階模型在不同馬赫數下的適用性.數值仿真結果表明，該氣動彈性降階模型能夠精確預測導彈模型在不同飛行條件下的非定常氣動力和導彈模型的氣動彈性頻率響應特性.

大長細比導彈，氣動力降階模型，遞歸Wiener模型，顫振邊界，極限環顫振

引言

飛行器氣動彈性力學是涉及飛行器設計、空氣動力學、結構動力學的交叉學科[1]，對于大展弦比飛機、大長細比導彈等柔性飛行器的研制尤為重要.在航空航天科技發展歷程中，曾有若干飛行器由于在設計階段未充分考慮氣動彈性問題，導致副翼效率下降、機翼顫振斷裂等.為了確保飛行器在使用過程中的安全，在飛行器研制過程中必須進行氣動彈性數值仿真，并通過風洞試驗、飛行試驗來驗證其氣動彈性特性.

非定常氣動力建模是氣動彈性力學研究的難點之一，其計算精度和效率直接影響到氣動彈性分析的精度和效率.在20世紀30年代，Theodorsen提出了適用于二元機翼的非定常氣動力模型[2]，隨后又有人又提出了核函數法[3]和偶極子網格法[4]，可分別求解三維振蕩機翼和復雜升力面的非定常氣動力.此后隨著計算能力提升，用計算流體力學(computational flui dynamics,CFD)[5]求解歐拉方程和N-S方程獲得了非定常氣動力.航空航天界普遍認為，CFD方法給出的非定常氣動力最接近實際，但該方法巨大的計算量限制了其在氣動彈性力學領域的應用.

因此，許多學者嘗試利用不同方法構造低維、高精度的空氣動力降階模型來代替CFD，在此基礎上進行飛行器氣動彈性/氣動伺服彈性分析[6].關于降階模型的研究可以分為3類：第1類是利用子空間方法構造降階模型，如特征正交分解(proper orthogonal decomposition,POD)方法[78]；第2類是依賴廣義差值算法，如徑向基函數、Kriging[9]等方法；第3類是采用基于輸入輸出的系統辨識算法構造降階模型，如神經網絡算法[1011]、Volterra級數[12].目前，上述氣動模型降階方法[13]在預測外形較為簡單的氣動彈性問題方面取得了成功，但對于外形復雜的非線性氣動彈性/氣動伺服彈性問題尚缺少充分研究.

早期導彈的結構剛度較大，氣動載荷與結構彈性變形的耦合不明顯，故在設計中可不考慮彈體結構的氣動彈性效應.近年來，為了滿足高機動、高速度等要求，導彈的長細比大幅增大[14]，有的達到20以上.此時，極易發生彈體剛體模態和彈性模態相耦合的氣動彈性問題，對導彈的飛行性能產生嚴重影響.因此，有必要對大長細比導彈進行氣動彈性/氣動伺服彈性分析.例如，楊超和吳志剛[15]用細長體理論和氣動導數方法分別計算作用于導彈的非定常氣動力，并分析了考慮導彈剛體平動、轉動和一階彎曲振動情況下的氣動伺服彈性穩定性問題，發現兩種方法計算的導彈氣動伺服彈性穩定性結果一致.在此基礎上，吳志剛和楊超[16]基于準定常氣動力分析了導彈在連續陣風和離散陣風下的氣動伺服彈性系統響應和穩定性，其結果表明結構彈性模態對控制器設計存在不利影響.全景閣等[17]采用當地活塞流理論研究軸向載荷對大長細比導彈氣動彈性穩定性影響，發現大長細比導彈的剛性模態和彈性模態極易發生耦合失穩現象，且失穩速度隨軸向載荷增大而降低.

上述研究采用簡化的氣動力模型，其計算效率較高，但結果的有效性受到簡化氣動力模型的制約.為了提高計算結果的有效性，需要發展基于CFD的高精度氣動彈性/氣動伺服彈性分析方法，同時又需要對基于 CFD的氣動力模型進行降階，進而提高計算效率.此外，大部分導彈采用全動平尾控制飛行姿態，且全動平尾與彈體之間留有間隙，通常的CFD網格處理方法(如嵌套網格等)會增加網格生成與流場計算的復雜程度，因此還需要簡化網格處理方法.

本文基于已有的遞歸Wiener模型降階方法，利用CFD計算數據作為降階模型的輸入輸出來實現氣動力模型降階[18]，并首次將其與導彈結構有限元模型相結合，構造大長細比導彈氣動彈性模型.為了驗證降階模型的有效性并獲得使用經驗，先將其應用于相對簡單的BACT機翼的氣動彈性分析；然后再將其應用于較為復雜的某大長細比導彈的氣動彈性分析.在大長細比導彈模型的氣動力CFD計算中，對舵面偏轉采用blended mesh方法來簡化處理控制面間隙，在網格生成和流場計算程序不變的前提下，模擬導彈全動平尾偏轉.

1 非線性氣動力降階方法

1.1 遞歸Wiener模型

遞歸Wiener模型是若干個Wiener單元的組合，每個Wiener單元由前置線性部分和后置非線性部分串聯組成，能夠較為精確地模擬非線性、時滯等因素.單元的線性部分可由傳遞函數、狀態方程等線性動力系統的數學模型來描述，非線性部分可采用非線性函數、分段非線性函數、神經網絡等數學模型來描述.

在本研究中，Wiener單元的線性部分采用狀態方程描述，非線性部分采用神經網絡描述，其數學表達式如下

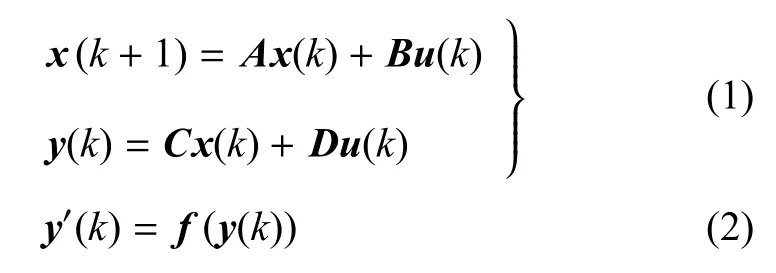
其中，x∈Rp,u∈Rm,y∈Rn和y′∈Rn分別為線性部分的狀態向量、輸入向量、輸出向量和非線性部分輸出向量；A ∈ Rp×p,B ∈ Rp×m,C ∈ Rn×p和 D ∈ Rn×m分別為線性部分的系統矩陣、輸入矩陣、輸出矩陣和直接反饋矩陣；f為非線性神經網絡系統.

遞歸 Wiener模型采用多層 Wiener單元構成復合系統，其模擬復雜非線性因素的能力強于單層Wiener單元.采用輸入輸出數據訓練遞歸Wiener模型時，第一層訓練數據即為輸入輸出訓練數據，第i層訓練數據中輸入數據不改變，輸出數據為原始輸出數據與前i-1層Wiener單元輸出數據之差，可以理解為下一層Wiener單元彌補了前面i-1層Wiener單元逼近能力的不足.訓練結束后，遞歸Wiener模型的最終輸出為

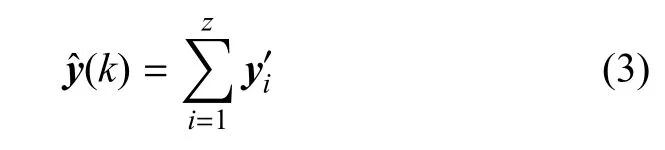
1.2 遞歸Wiener模型辨識

對遞歸Wiener模型中的線性部分，可采用魯棒子空間(PBSID)算法[1920]辨識其系統矩陣.該算法具有辨識精度高、模型階數低、辨識系統穩定性高和可應用于閉環系統等優點，而且該方法僅需輸入輸出數據.利用PBSID方法辨識由CFD獲得的系統廣義位移與廣義氣動力數據，即可求得線性非定常氣動力狀態方程的參數.

線性部分的向量自回歸表達式為

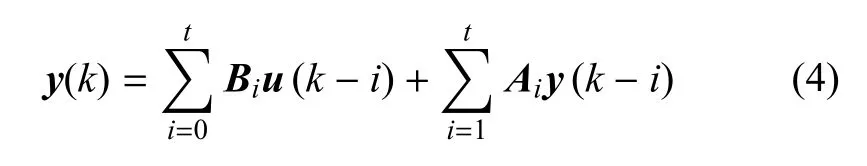
其中，t∈ R+為過去影響因子，Ai∈ Rp×p和 Bi∈ Rp×m為需辨識的參數.為了簡化辨識，可將Ai和Bi整合為矩陣Θ∈Rn×(m(t+1)+nt)統一辨識，故定義

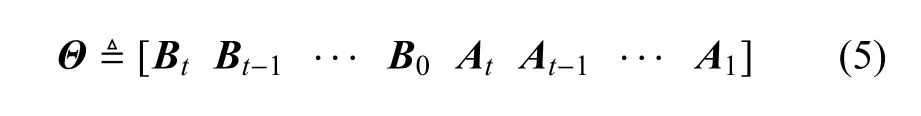
通過最小二乘法可辨識獲得

其中，(·)+為廣義逆矩陣符號，Y ∈Rn×(N-t)和 Ω ∈R(m(t+1)+nt)×(N-t)定義如下

方程(1)的系數矩陣A,B,C,D可以通過子空間辨識方法來確定[2021]，將辨識結果記為

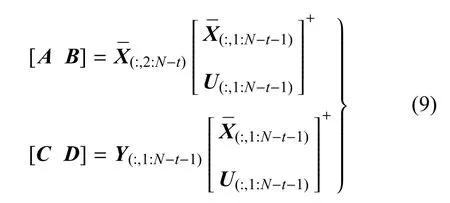
其中u∈Rm×(N-p)定義如下

為了計算狀態矩陣ˉX，定義

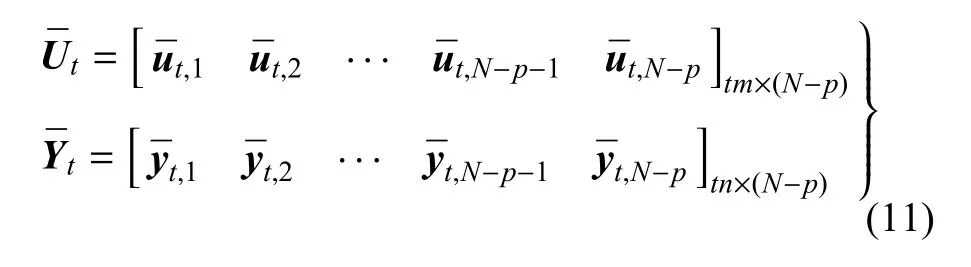
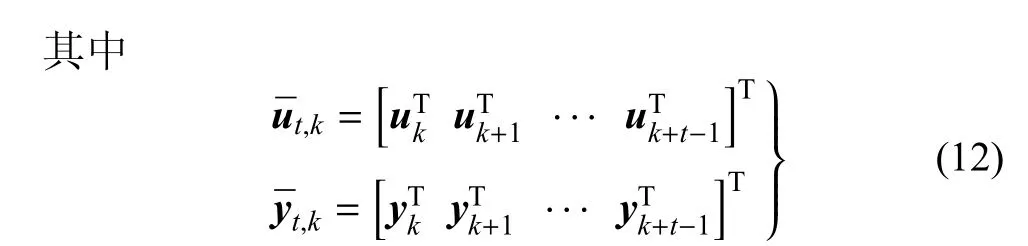
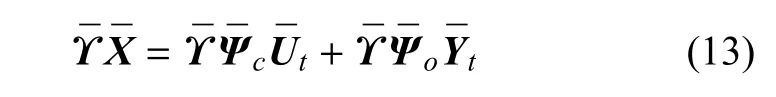
其中

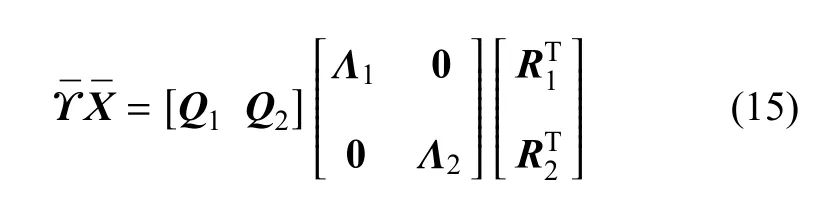
令Λ2≈0，可求得狀態矩陣ˉX為

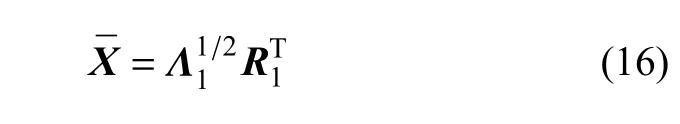
在辨識非線性神經網絡參數時，首先求解白噪聲輸入下遞歸Wiener模型的線性部分輸出數據，將線性部分輸出數據和CFD計算數據作為神經網絡辨識所需的訓練信號，利用 Levenberg-Marquardt(LM)[22]辨識算法確定遞歸Wiener模型中非線性神經網絡參數.神經網絡的神經元采用tanh函數，其個數z由經驗給定.對于單層Wiener單元，z取1到12即可.獲得非線性神經網絡參數后，應將遞歸Wiener模型的線性和非線性參數再次采用LM方法進行聯合辨識.在辨識過程中對參數進行適當調整，以提升降階模型所預測氣動力與真實氣動力的吻合度.

用同樣方法辨識下一層Wiener單元前，需計算本層預測氣動力與真實氣動力的VAF值作為循環是否結束的標志，其中VAF值定義為

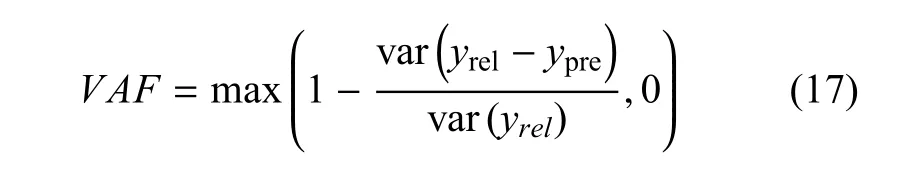
VAF值隨著兩個信號相同程度增加而變大，當VAF值到達100%時，代表兩個信號完全相同.若計算i層的VAF值低于5%，則認為該層未包含逼近真實氣動力所需必要信息，可停止遞歸過程，取前i-1層組成遞歸Wiener模型.

2 氣動彈性模型

為了采用遞歸 Wiener模型較為細致地研究飛行器結構氣動彈性問題，本文考察兩個氣動彈性模型，即較為簡單的BACT機翼模型和較為復雜的大長細比導彈模型.

BACT模型是基于NACA0012翼型生成的矩形機翼，具有后緣控制面和上下表面擾流片.該模型作為顫振主動抑制研究的標準模型，運動形式較為簡單且CFD網格量較小，獲得的降階模型可用于顫振主動抑制研究.因此，本文首先基于BACT機翼進行降階模型精度對比.將BACT機翼作為三維剛性機翼模型，其運動形式為剛體運動，而且其氣動布局簡單，氣流流動分布較為平緩.

BACT機翼模型能夠作為三維剛性機翼處理，原因在于其根部由PAPA系統支撐，系統彈性模態的固有頻率遠高于剛體沉浮、俯仰模態的固有頻率，彈性模態對結構動力學行為影響較小，因此可僅考慮沉浮和俯仰兩個剛體自由度.對于其控制面，僅考慮不同偏轉角對氣動力的影響，不考慮舵面變形引起的氣動彈性.根據拉格朗日方程，BACT機翼模型的運動微分方程如下

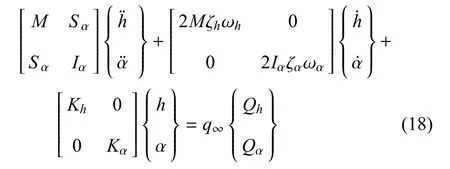
其中，h,α為沉浮位移和俯仰角位移;q∞為無窮遠處流場動壓；Qh和Qα為非定常升力和力矩，它們是h,α及控制面偏轉角β的函數，其值由CFD或降階模型計算獲得.將方程(18)轉化為模態空間的運動微分方程如下

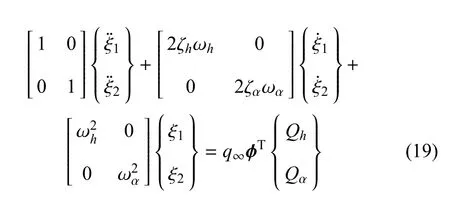
其中，φ是模態矩陣，ξ1和ξ2是第一、二階模態位移.方程(19)可寫作狀態空間方程

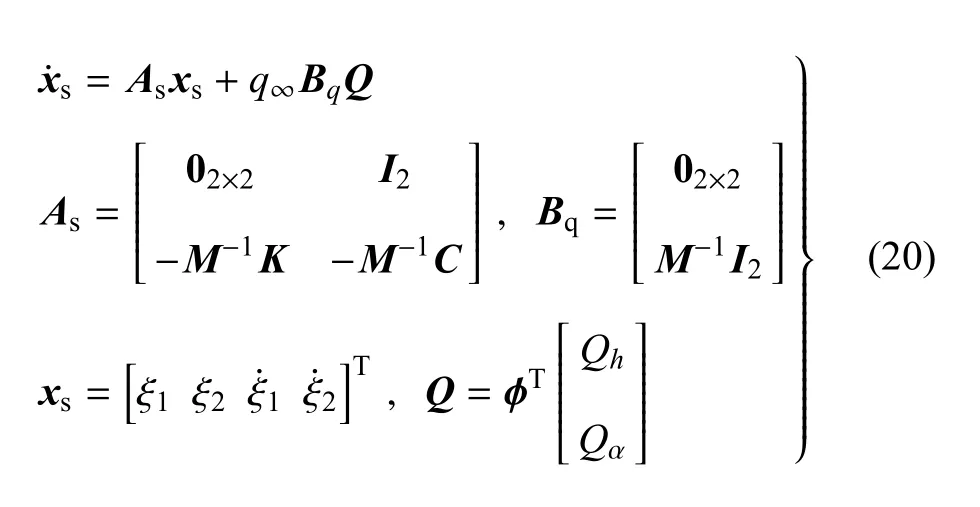
其中,xs為狀態矢量，Q為輸入矢量.

對于大長細比導彈的氣動彈性問題，本文不考慮其剛體運動引起的氣動力變化，僅考慮其前兩階彈性振動模態引起的氣動彈性響應.對于其控制面，同樣僅考慮不同偏轉角對氣動力影響，不考慮舵面變形引起的氣動彈性.利用有限元程序獲得該導彈模型的廣義質量歸一化模態信息后，即可建立與方程(19)類似的模態空間下運動微分方程，并轉化為狀態方程(20)形式.

圖1是大長細比導彈模型的幾何造型和有限元網格.采用Patran/Nastran建立結構有限元模型，計算獲得其前兩階彈性模態如圖2所示，對應的模態阻尼比取為零.

建立上述模型的氣動彈性方程后，即可根據其運動過程中受到的非定常氣動力，采用數值積分方法求解任意時刻的系統狀態.

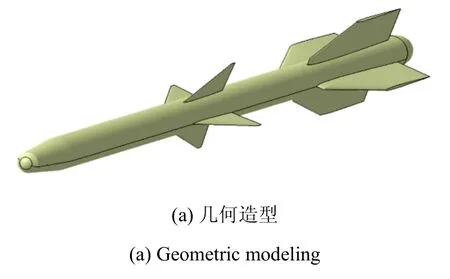
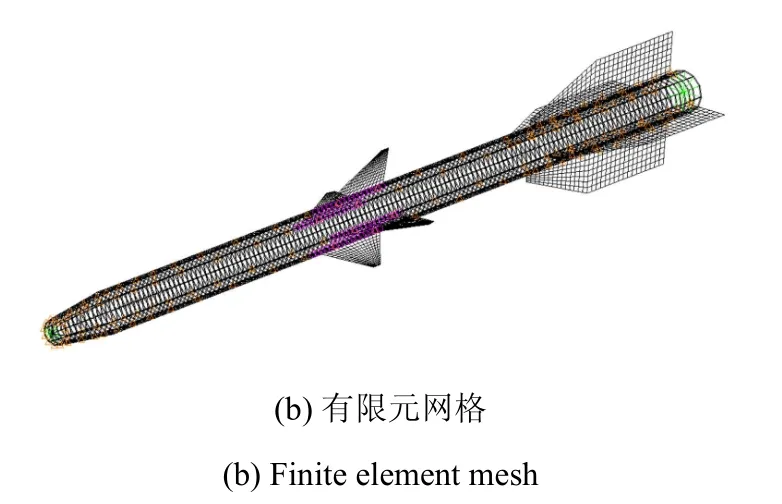
圖1 大長細比導彈模型及其有限元模型Fig.1 A slender missile model and the mesh of finit elements

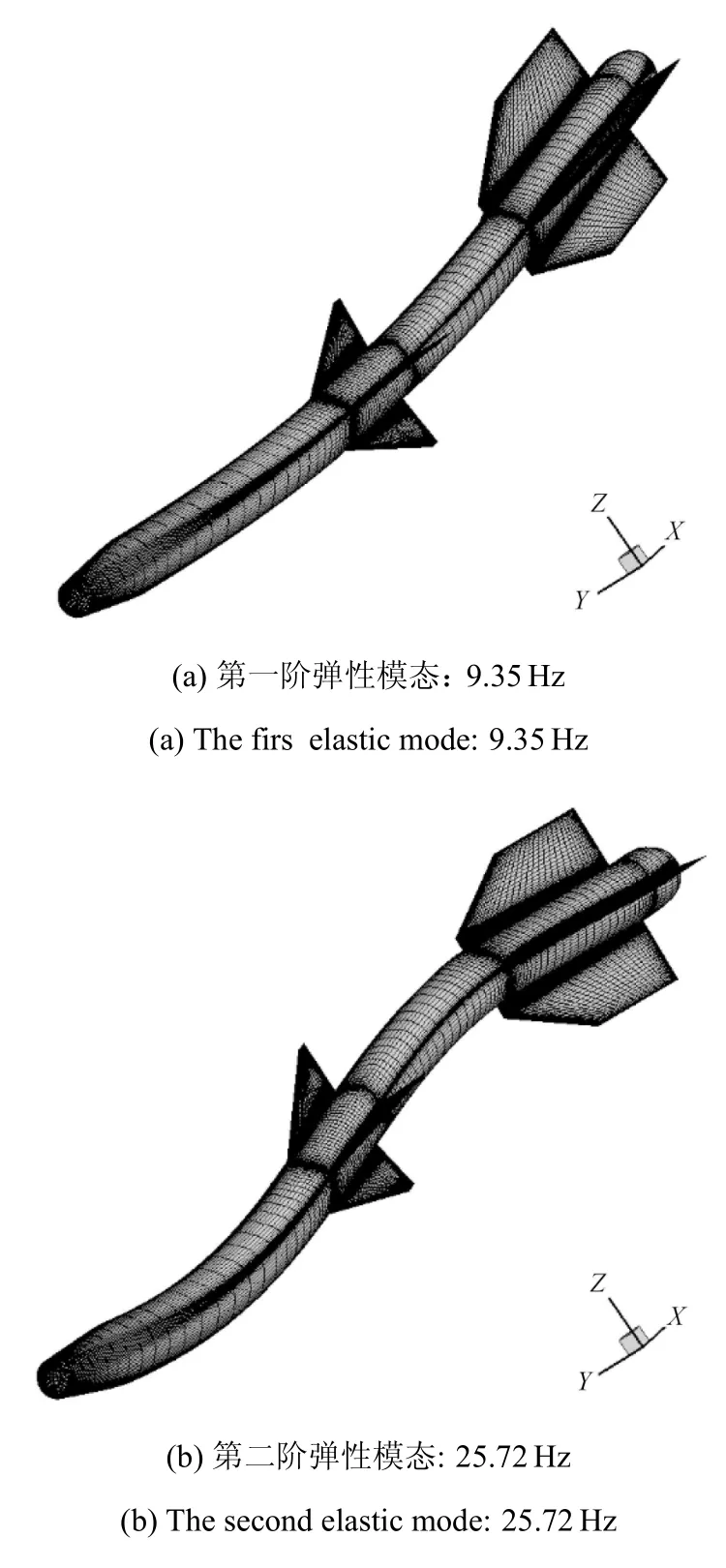
圖2 大長細比導彈模型的前兩階彈性模態Fig.2 First two elastic modes of the slender missile model

3 算例與分析

將第1節提出的非線性氣動力降階方法應用于第2節的兩個模型，分別構造其氣動力降階模型.建立氣動力降階模型時，首先基于模型的幾何外形建立CFD網格，隨后進行CFD計算獲得訓練模型所需的氣動力數據.為了保證CFD計算的氣動力訓練信號能夠包含所研究氣動彈性響應所對應的非定常氣動力，需要給遞歸Wiener模型提供廣義位移運動信號作為計算流場參數.鑒于有限帶寬白噪聲信號可包含結構的寬帶動響應，因此將其作為結構模型的廣義位移和控制面偏轉角信號，然后通過CFD計算結構在此狀態下受到的非定常氣動力.

為了考察該降階模型對于復雜氣動力模擬的精度，文中隨后對某大長細比導彈模型建立降階模型，并檢驗其預測初始擾動下氣動彈性響應的精度.大長細比導彈是三維彈性體，氣動布局比較復雜.本文側重于氣動彈性問題，故僅考慮導彈的彈性變形引起的氣動力變化，不考慮其剛體運動引起的氣動力變化.

3.1 BACT機翼模型的氣動彈性響應

考察帶后緣控制面的BACT機翼模型，方程(18)中參數如下[23]：M =88.73kg,Sa=0.063kg·m,ζh= 0.0014,ζα= 0.001,ωα= 32.72rad/s,ωh=21.01rad/s,Kh=39199.03N/m,Kα=4067.43N/m,Iα=3.80kg·m2.

采用 N-S方程計算 BACT機翼模型周圍的流場，將比熱比取為 1.132，雷諾數取為 3.96×106，BACT機翼模型的廣義位移最大值為0.2，控制面偏轉角最大值為5?，動響應頻率范圍均為0～300rad/s.在CFD計算中，物理時間步長為1ms，訓練信號取為6000步，即6000組訓練數據.為了驗證降階氣動力模型在不同條件下的精度，對控制面偏轉角給予頻率25.13Hz、幅值4?的正弦信號，用CFD計算BACT機翼模型的氣動力，作為考察氣動力降階模型精度的參考依據.

給定馬赫數0.63,0.70,0.71,0.75,0.77,0.8,0.82,0.825，通過CFD計算獲得氣動力數據后建立氣動力和氣動彈性降階模型.現重點討論馬赫數0.825飛行條件下的模型精度.此時，取狀態方程階次為8、神經網絡的神經元數為10，辨識出的遞歸Wiener模型逼近非線性氣動力的精度最高.圖3給出CFD計算的廣義氣動力訓練數據和降階模型預測的廣義氣動力對比；其中一階廣義力信號的VAF值為99.86%，二階廣義力信號的 VAF值為 99.77%.圖 4給出CFD計算的廣義氣動力驗證數據和降階模型預測的廣義氣動力對比；其中一階廣義力信號的VAF值為99.89%，二階廣義力信號VAF值為的99.47%.在其他馬赫數下，CFD計算和降階模型預測的廣義氣動力VAF值均高于99%.這說明，在不同飛行條件下建立的氣動力降階模型均能夠精確預測氣動力，即該降階模型對很寬的飛行速度范圍具有適應性.

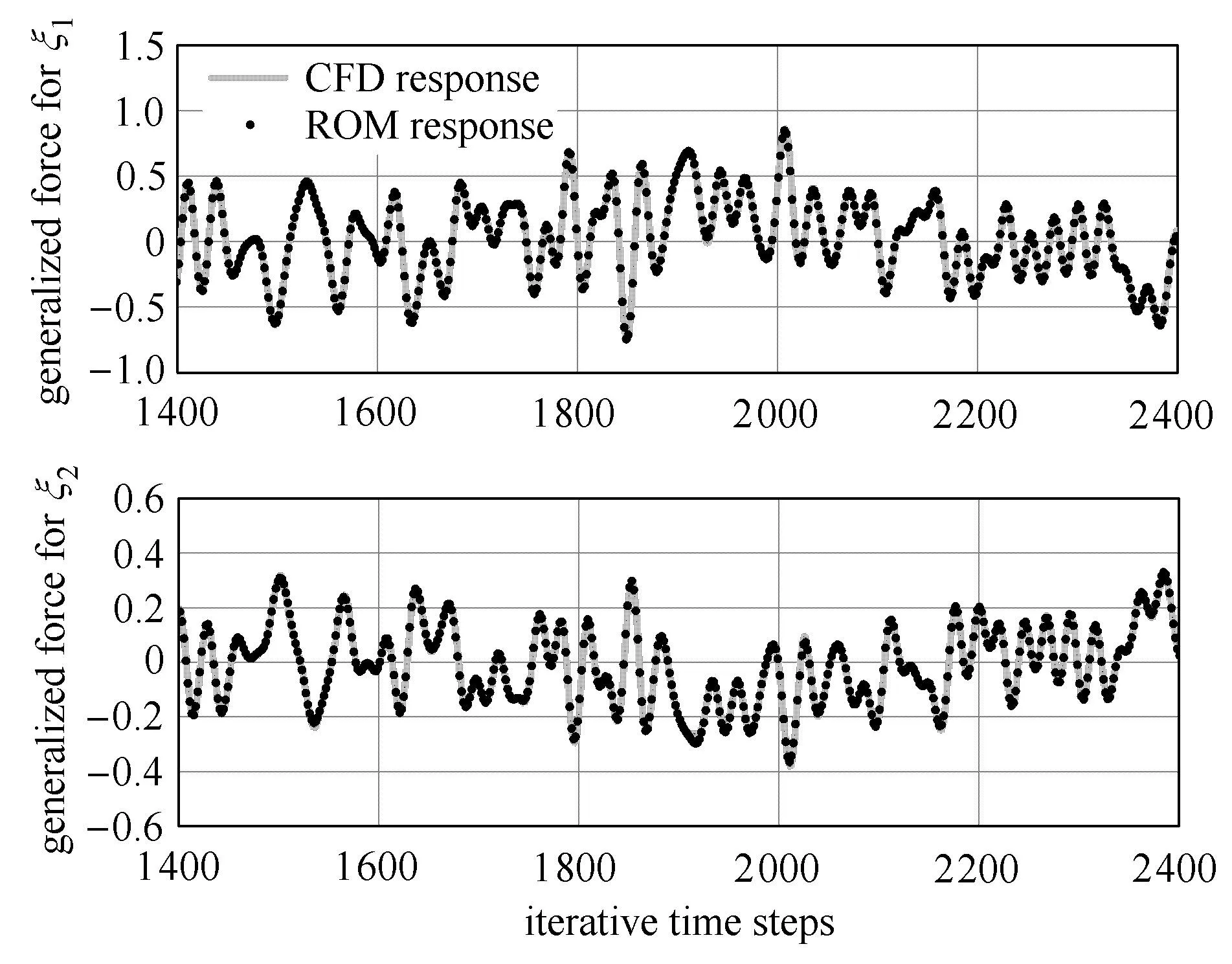
圖3 BACT機翼模型的氣動力訓練信號Fig.3 Training signal of aerodynamic load on the BACT wing model

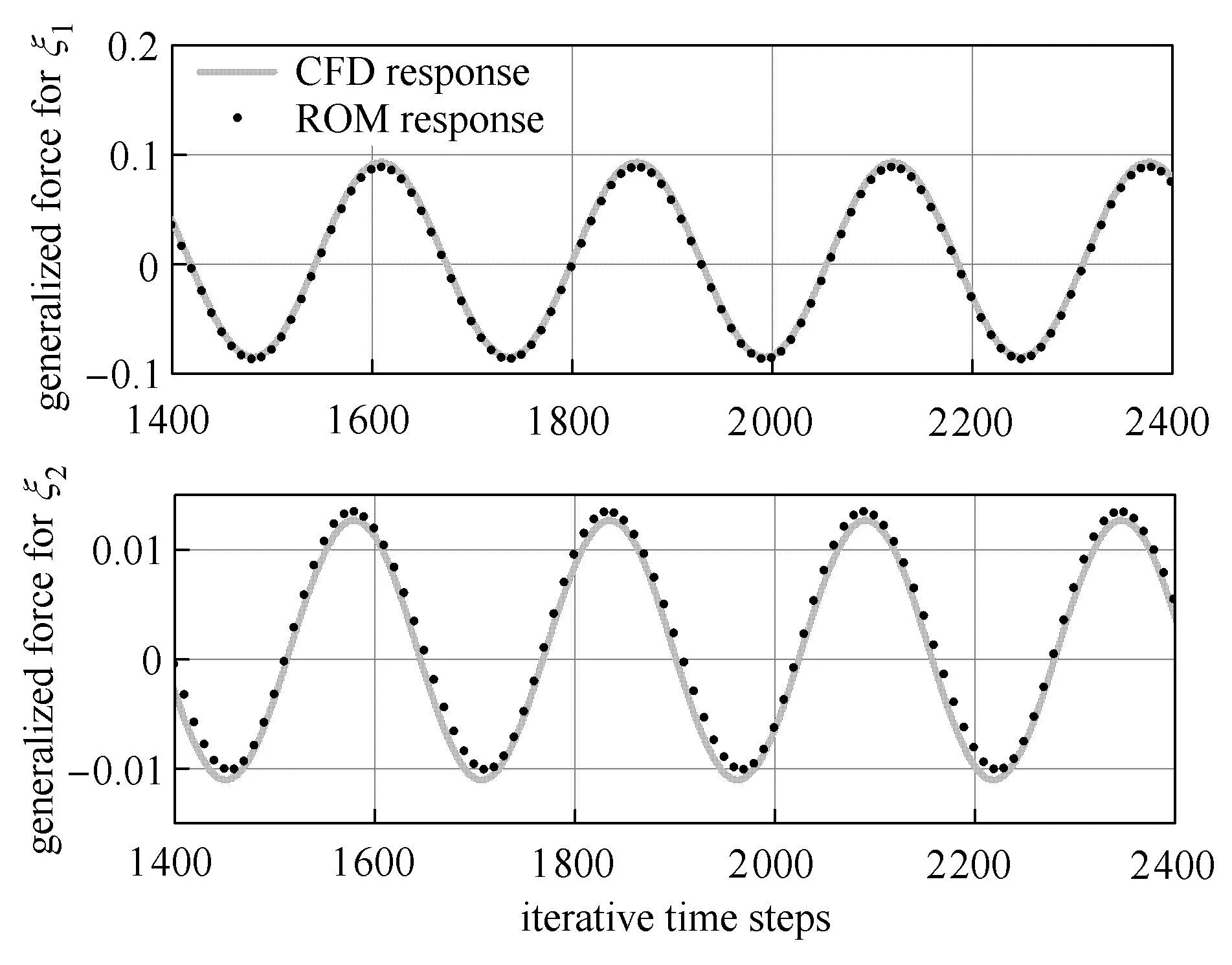
圖4 BACT機翼模型的氣動力驗證信號Fig.4 Verificatio signal of aerodynamic load on the BACT wing model

經過上述預測精度驗證后，可將氣動力降階模型并入結構氣動彈性方程，進而計算結構氣動彈性響應，尤其是預測顫振邊界[2426].為了驗證該氣動彈性降階模型預測結構顫振邊界的能力，在上述馬赫數下建立氣動彈性降階模型，并逐漸增大動壓尋找顫振動壓邊界.為了考核該降階模型預測顫振邊界的精度，將其與CFD計算的顫振邊界對比并計算誤差，同時與線性降階模型預測的顫振邊界進行對比，結果如圖5所示.由圖可見，遞歸Wiener降階模型能夠精確預測各馬赫數下的顫振動壓，其誤差均處于2%以下，比線性降階模型預測的顫振邊界精度大為提高.這說明，該降階模型能夠精確模擬非線性氣動彈性現象.

為了進一步考察降階模型預測非線性氣動彈性的能力，現考察極限環顫振問題[2732].在馬赫數0.825、動壓9.10kPa的飛行條件下，基于CFD和降階模型得到的氣動力與結構動力學相耦合，獲得的極限環顫振幅值對比結果如圖6.由圖6可見，降階模型能較為精確地預測極限環顫振幅值，證明遞歸Wiener模型有模擬較強非線性氣動力的能力.

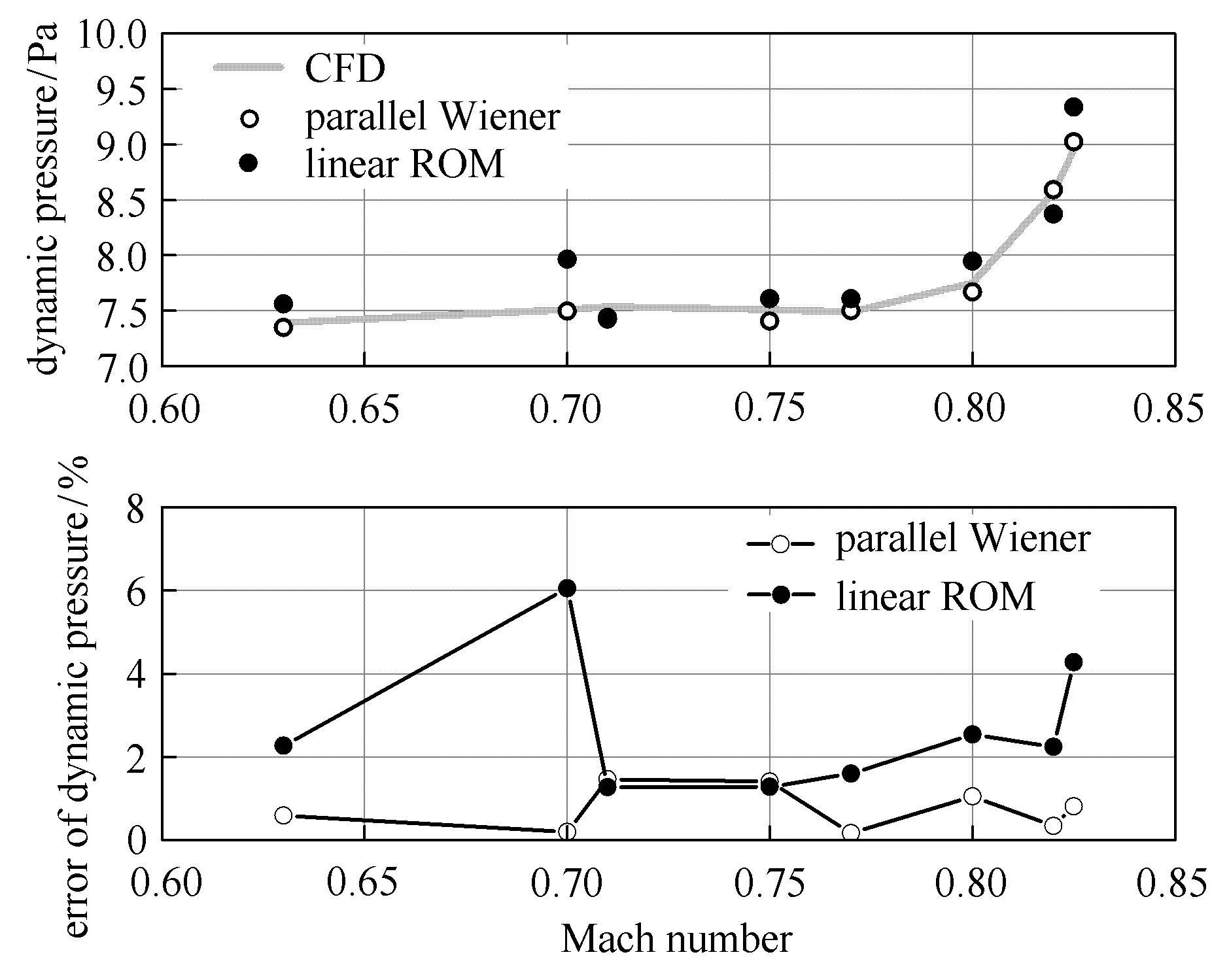
圖5 BACT機翼模型的顫振邊界Fig.5 Flutter boundary of the BACT wing model

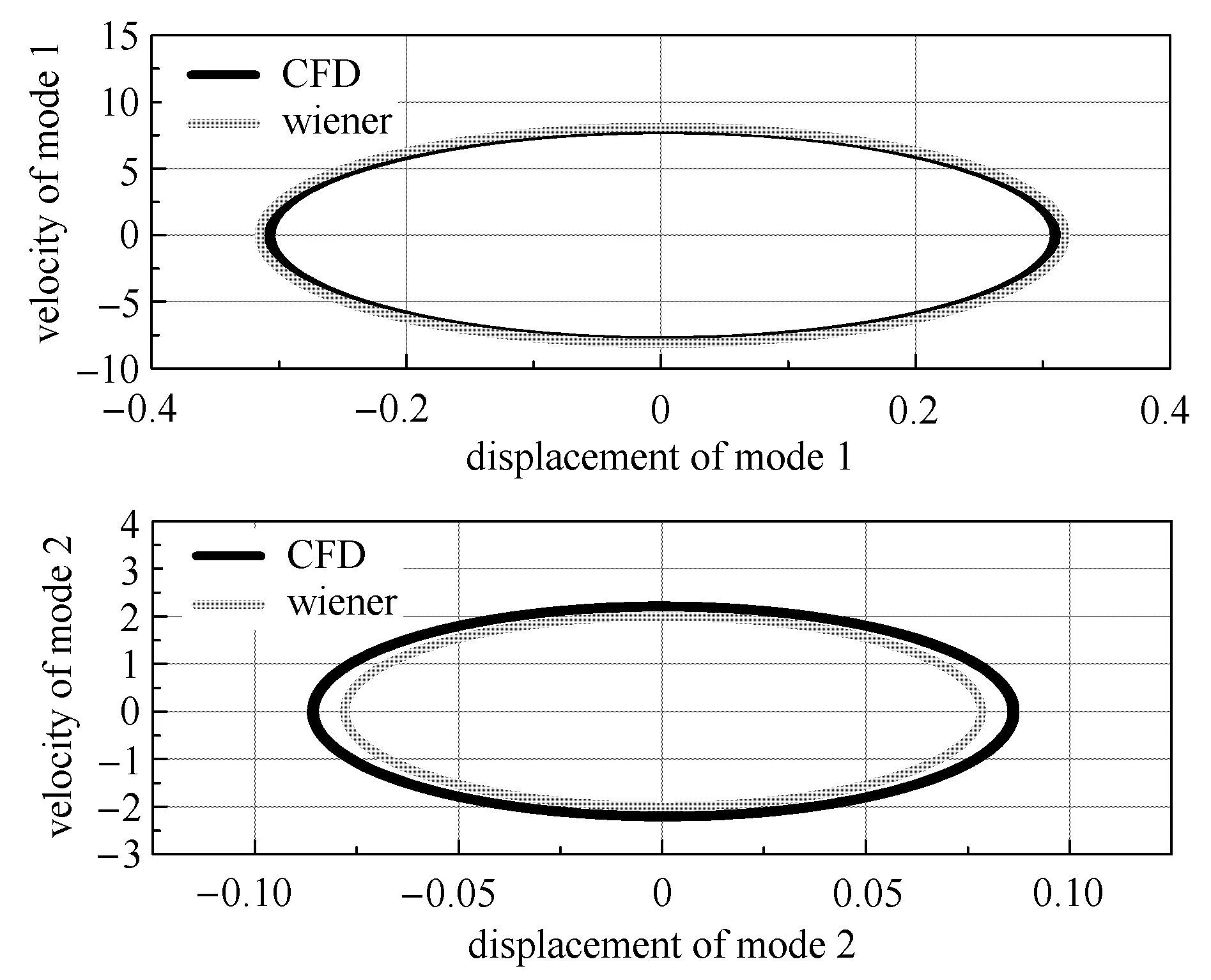
圖6 BACT機翼模型的極限環顫振幅值Fig.6 Amplitude of the limit cycle flutte of the BACT wing model

3.2 大長細比導彈模型的氣動彈性響應

基于歐拉方程計算導彈模型的流場，圖7是流場的CFD網格.圖8是在馬赫數0.8和2.0、攻角為0?的飛行條件下，計算得到的導彈模型表面壓力分布系數.由圖可見，導彈模型表面的壓力分布系數符合實際，因此可用該網格進行CFD計算.

在導彈飛行過程中，通常需要偏轉舵面來實現控制，精確計算舵面偏轉產生的非定常氣動力是進行導彈飛行控制的關鍵.為了計算舵面偏轉引起的氣動力載荷，通常要加密舵面和彈體間隙處的流場網格，或采用嵌套網格,而這使得網格生成和流場計算的復雜性顯著提高.為了簡化該問題，利用blended mesh方法描述舵面偏轉.該方法忽略舵面和彈體之間的間隙，將二者視為一個光滑曲面.偏轉后舵面上點的坐標為

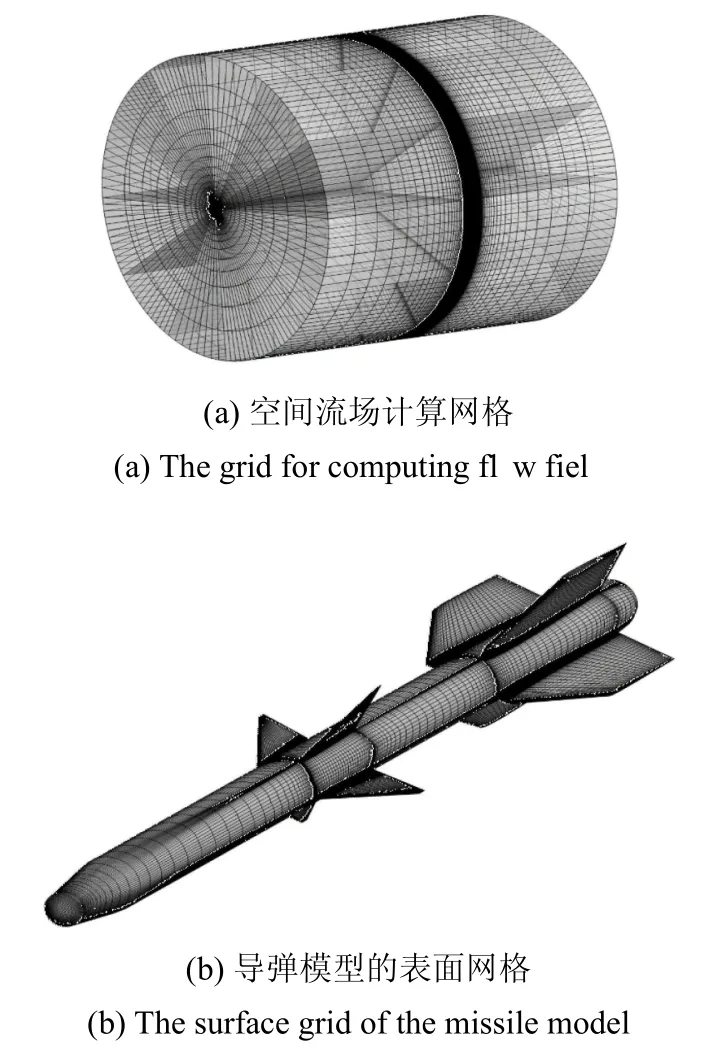
圖7 大長細比導彈的CFD網格Fig.7 CFD grid for a slender missel model

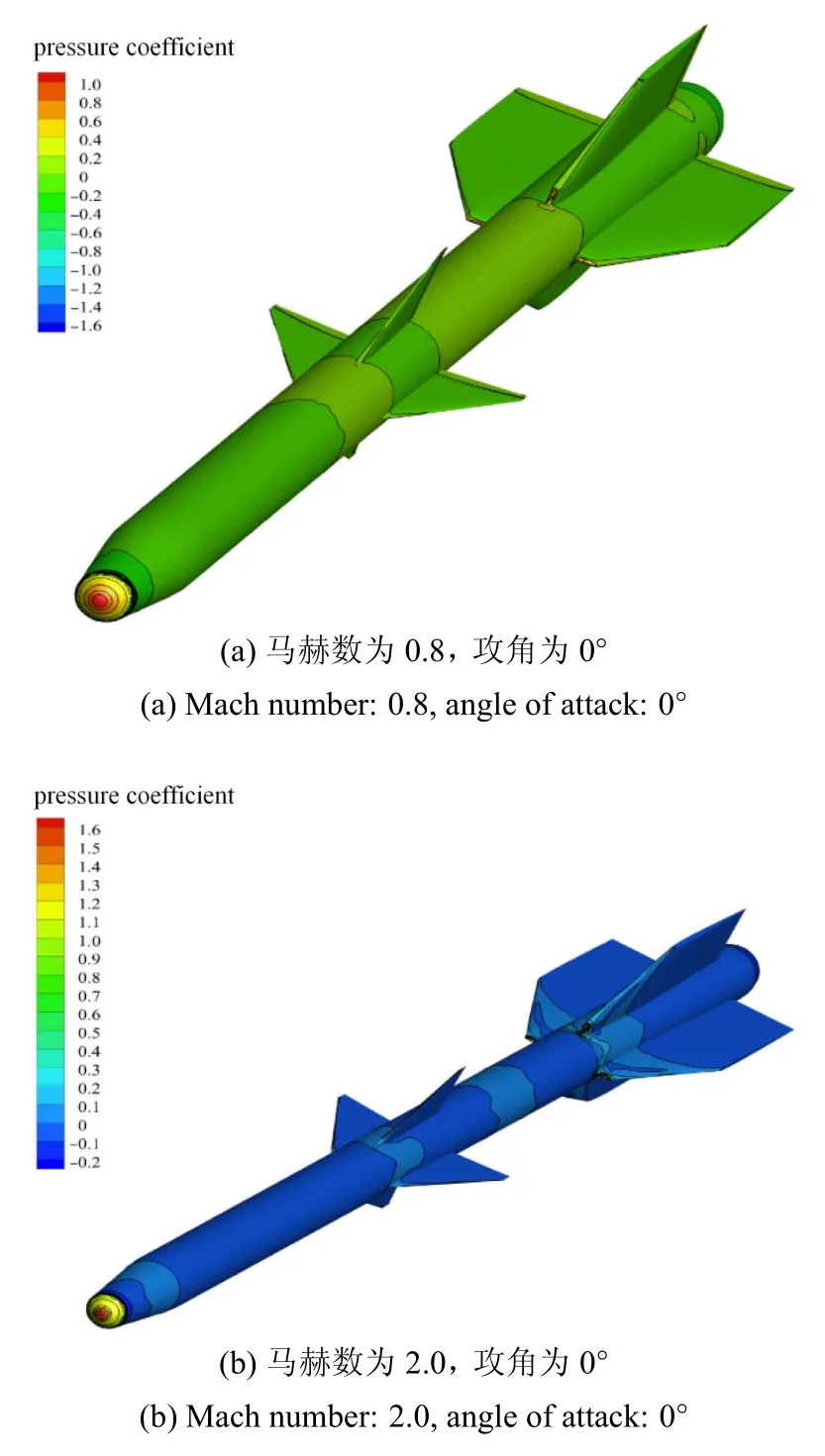
圖8 導彈模型表面壓力分布系數Fig.8 Surface pressure distribution coefficient on the slender missile model

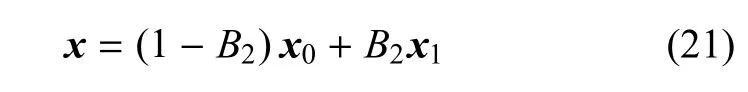
式中，x為經協調處理后的偏轉舵面上點的坐標，x0為未偏轉舵面上點的坐標，x1為未協調處理的偏轉舵面上點的坐標，協調參數B2定義為

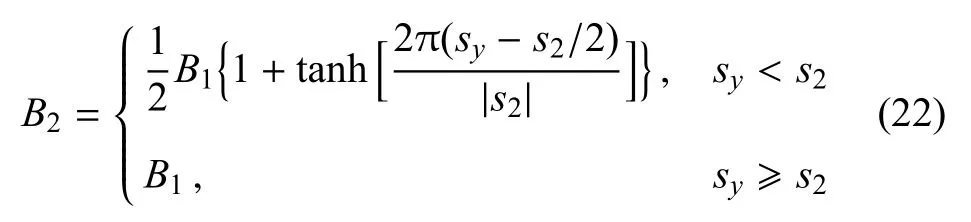
其中，sy為舵面上網格點與彈體—舵面間間隙之間的展向距離，s2為設定的展向協調寬度，B1為弦向協調參數，其定義如下

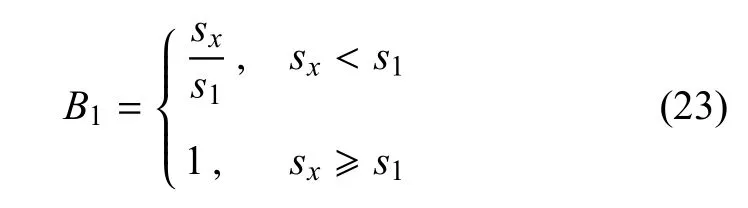
其中，sx為為舵面上網格點與舵面鉸鏈線之間的弦向距離，s1為設定的弦向協調寬度.為了驗證這種處理舵面偏轉的簡化方法，定義尾舵的鉸鏈線位于y=2500mm，展向協調參數s2和弦向協調參數s1分別取為10mm和20mm，尾舵偏轉3?和尾舵偏轉6?時導彈模型表面的CFD網格變形如圖9所示.

仍采用有限帶寬白噪聲信號作為結構響應訓練信號，其廣義位移最大值達1.2，控制面偏轉角最大值為3?，信號頻率范圍均為0～200rad/s.在CFD計算中，物理時間步長取為0.5ms，訓練信號取6000步，即6000組訓練數據.為了驗證降階模型的精度，給定控制面偏轉角為頻率為23.88Hz、幅值為2?的正弦運動.利用CFD計算導彈模型在此運動狀態下的廣義氣動力并和降階模型預測的廣義氣動力進行對比.

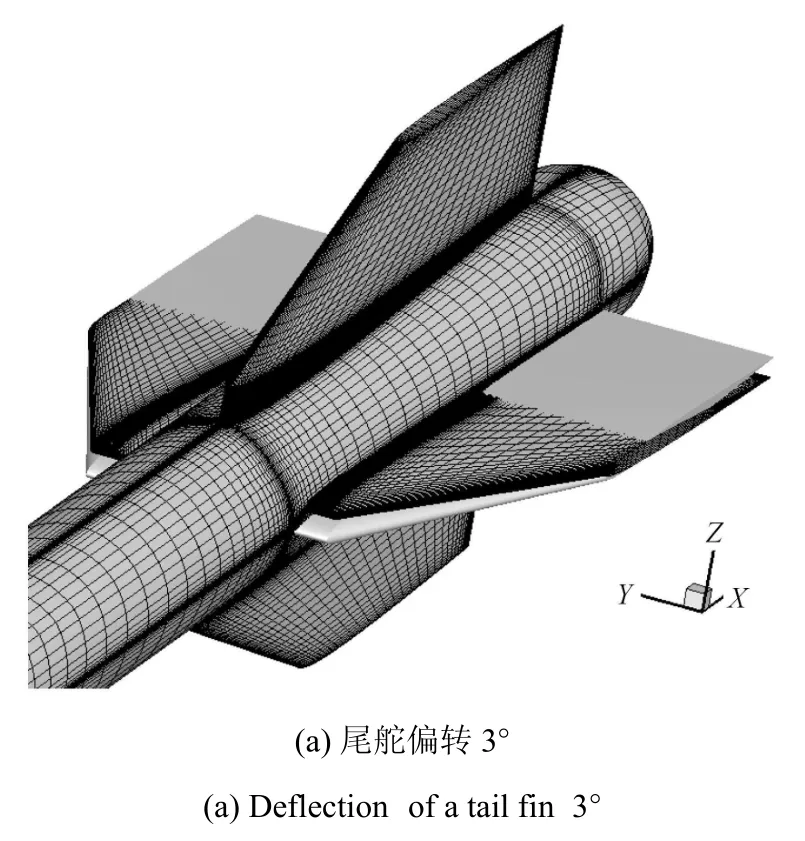
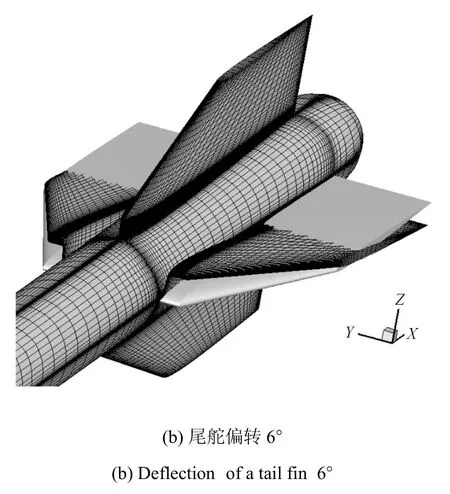
圖9 不同尾舵偏轉時導彈模型表面的CFD網格Fig.9 CFD grid on the missile model for di ff erent deflection of a tail fi

在馬赫數0.8時，取狀態方程階次為26，神經網絡中神經元個數為2，辨識的遞歸Wiener模型預測的非線性氣動力精度最高.圖10給出CFD計算的廣義氣動力訓練信號和降階模型預測的廣義氣動力信號對比.其中一階廣義力信號的VAF值為98.82%，二階廣義力信號的VAF值為97.23%.圖11是CFD計算的廣義氣動力驗證信號和降階模型預測的廣義氣動力信號對比.其中一階廣義力信號的VAF值為98.81%，二階廣義力信號的VAF值為97.84%.

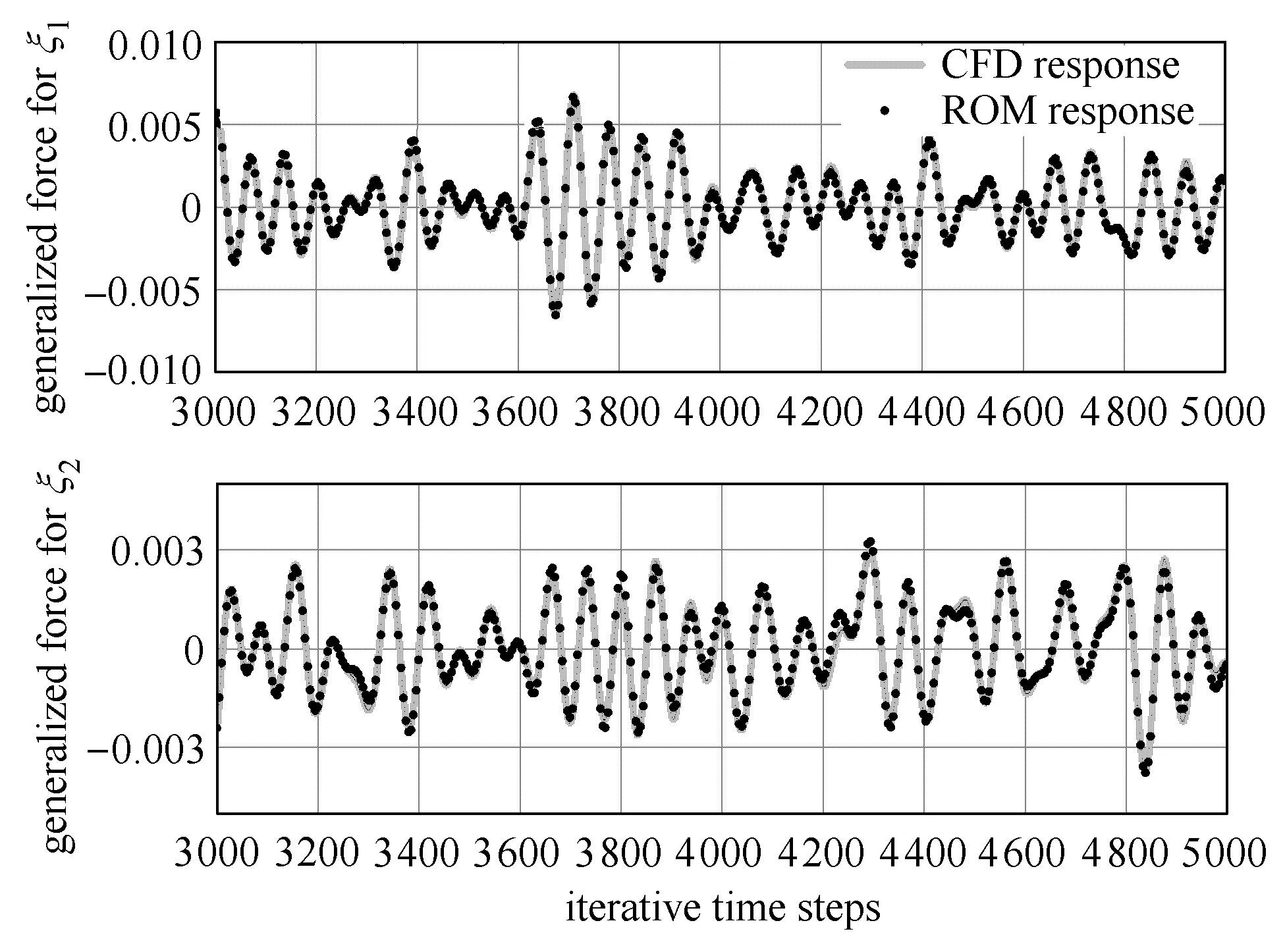
圖10 導彈模型的氣動力訓練信號Fig.10 Training signal of aerodynamic load on the missile model

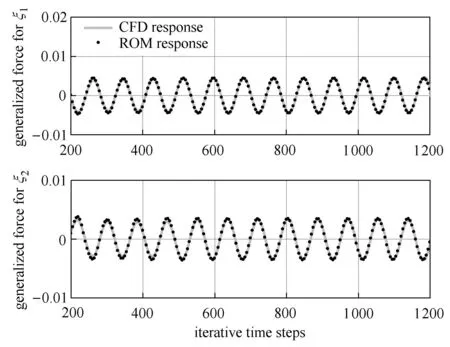
圖11 導彈模型的氣動力驗證信號Fig.11 Verificatio signal of aerodynamic load on the missile model

在馬赫數2.0時，取狀態方程階次為24、神經網絡中神經元個數為3，辨識出的遞歸Wiener模型預測非線性氣動力的精度最高.此時，CFD計算的廣義氣動力訓練信號與降階模型預測的廣義氣動力信號相比，一階廣義力信號的VAF值為99.94%，二階廣義力信號的VAF值為99.69%；而CFD計算的廣義氣動力驗證信號與降階模型預測相比，一階廣義力信號的VAF值為99.98%，二階廣義力信號的VAF值為99.82%.

由此可見，不論在亞音速、跨音速或者超音速條件下，遞歸Wiener模型均能精確模擬非線性氣動力，并對不同的馬赫數具有適應性.對于大長細比導彈模型，跨音速條件下的預測精度低于超音速，也同樣略低于BACT機翼模型在跨音速條件下的預測精度.但當飛行器模型在某一小幅度范圍內運動時，該模型仍能較為精確地預測復雜非線性氣動力.這表明該方法可應用于復雜飛行器模型的氣動力降階.

為了驗證大長細比導彈氣動彈性降階模型的有效性，在馬赫數 0.8條件下對比基于 CFD和遞歸Wiener模型所建立氣動彈性模型計算的氣動彈性響應.在給定第二階模態速度˙ξ2為10.0、其余模態位移和速度為零條件下，圖12給出用不同方法計算的氣動彈性響應對比.由圖可見，降階模型可精確預測短時間內的氣動彈性響應問題.需要指出的是，當降階模型用于計算長時間范圍內的氣動彈性響應時，誤差會比較大.表1是計算圖12中氣動彈性響應所需的時間對比.可以看出，大長細比導彈氣動彈性降階模型可在較為精確預測氣動彈性響應的前提下，大幅度縮短計算所需時間.

為進一步考察導彈模型的氣動彈性響應，分別在馬赫數0.8和2.0、動壓45.3kPa的條件下，建立導彈氣動彈性降階模型.設導彈控制面角度運動規律為多組不同頻率的正弦運動，其幅值均為2?，頻率由5Hz連續變化到30Hz.利用導彈氣動彈性降階模型計算此狀態下導彈模型的各階模態位移，對穩定的氣動彈性響應實施FFT.圖13是馬赫數0.8和2.0條件下的一階模態幅頻、相頻曲線，圖14是對應的二階模態幅頻、相頻曲線.由計算結果可見，導彈模型的各階模態位移振動幅值在控制面偏轉運動頻率位于其固有頻率附近時達到最大.當馬赫數為0.8時，一階模態位移峰值點為(8.6,0.752)，二階模態位移峰值點為(24.8,0.443)；當馬赫數為2.0時，一階模態位移峰值點為(9.2,0.763)，二階模態位移峰值點為(25.5,0.216).由此可見，共振頻率隨著馬赫數增大而增大.對應兩個不同馬赫數，一階模態位移峰值僅差僅1.3%，差距較小；而馬赫數0.8時，二階模態位移峰值比馬赫數2.0時高102.2%，差距較大.這說明，在跨音速條件下，大長細比導彈的氣動彈性問題更為顯著.需要指出的是，圖13和圖14的計算結果未與CFD計算結果進行對比.一方面，因為在前面的算例中已對降階模型在預測氣動力、氣動彈性等方面的能力與CFD計算結果進行了對比，證實其可替代CFD來預測控制面激勵下的導彈氣動彈性響應.另一方面，由于CFD計算量大，消耗時間過長，難以進行全面分析對比.

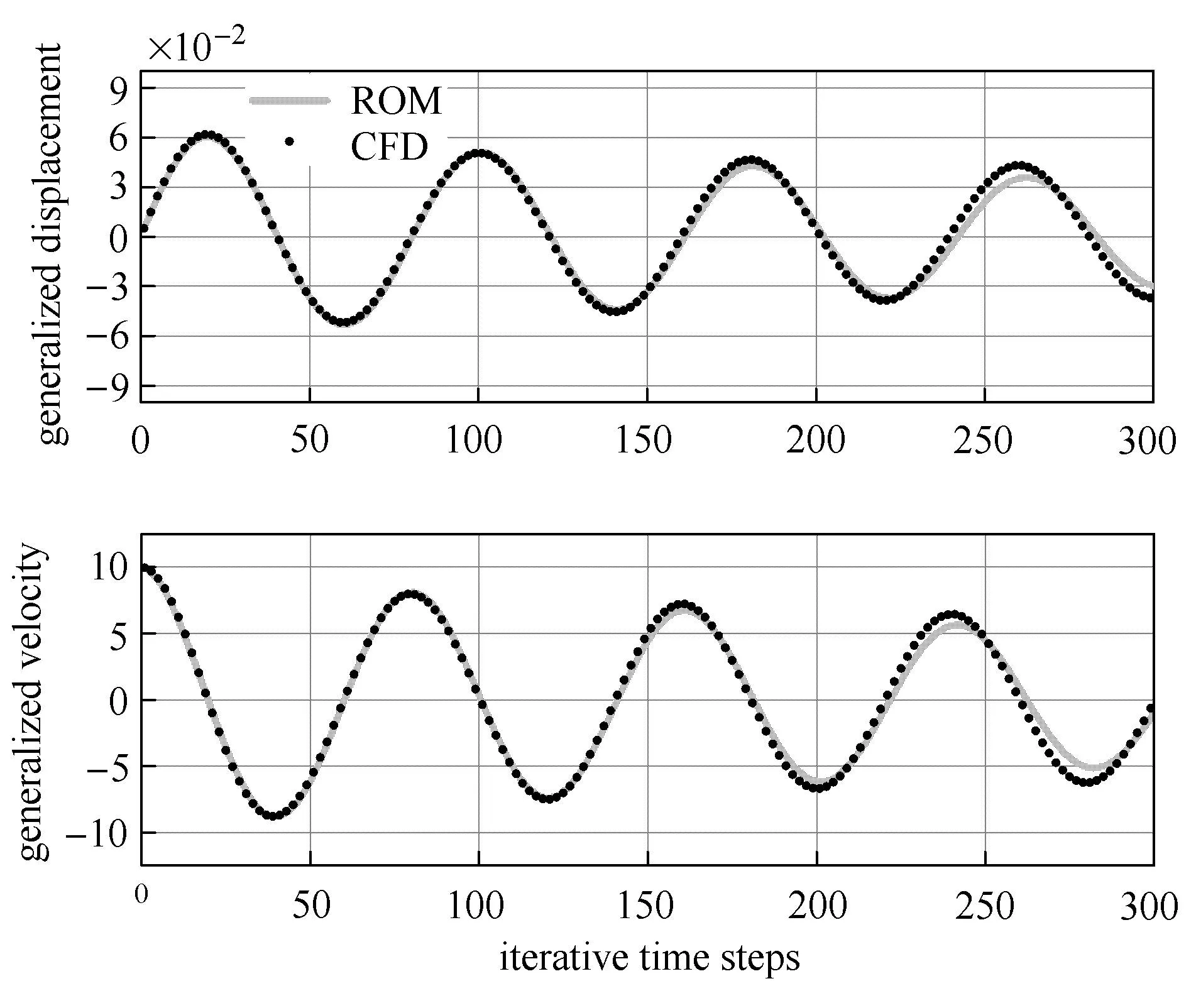
圖12 導彈模型的氣動彈性響應Fig.12 Aeroelastic responses of the missile model

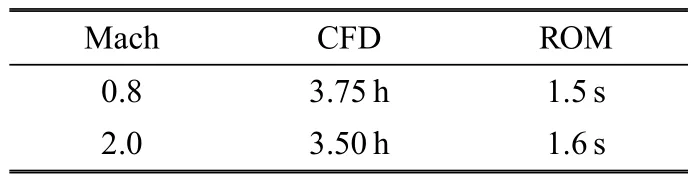
表1 導彈模型氣動彈性響應計算時間Table1 Computation time for aeroelastic responses of the missile model

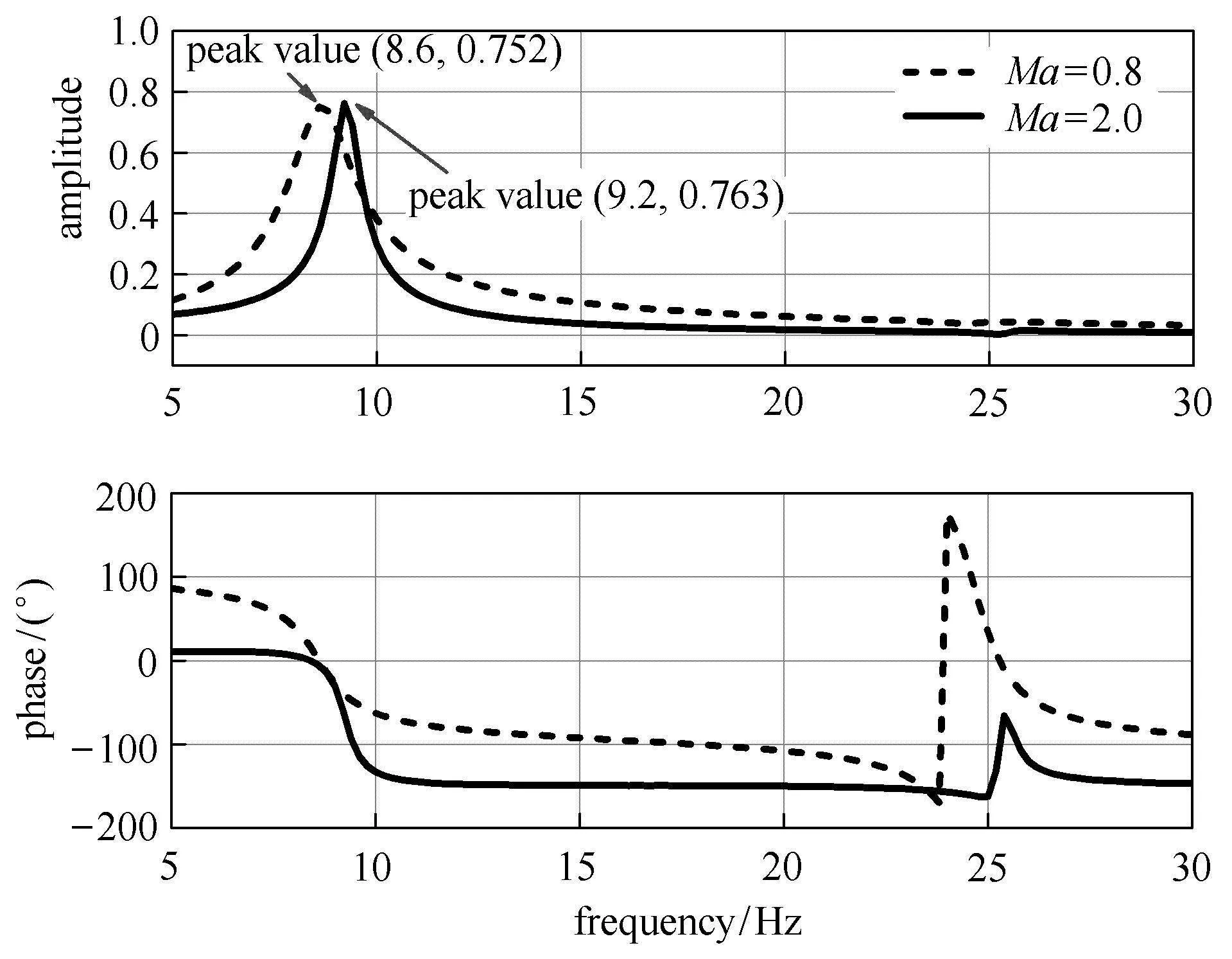
圖13 導彈模型的一階模態位移頻譜Fig.13 The frequency spectrum of the first-orde modal displacement of the missile model

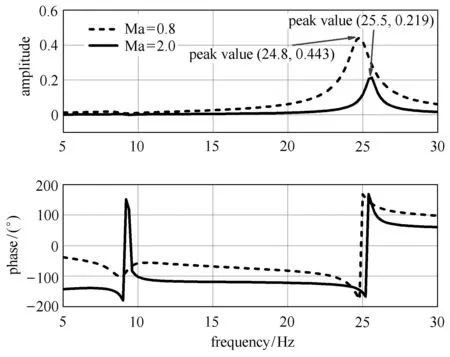
圖14 導彈模型的二階模態位移頻譜Fig.14 The frequency spectrum of the second-order modal displacement of the missile model

4 結論

本文基于 CFD計算的氣動力數據構造遞歸Wiener模型，在亞、跨、超音速等多馬赫數條件下建立了大長細比導彈的氣動彈性降階模型.數值計算結果表明，遞歸Wiener模型可描述較寬馬赫數范圍的氣動彈性問題，并且能夠精確預測顫振邊界、極限環顫振幅值、給定初始狀態的氣動彈性響應.所建立的氣動彈性降階模型能大幅度降低CFD計算消耗的時間，可方便地應用于后續主動控制器設計.研究發現，該降階模型應用于氣動外形復雜的大長細比導彈時，其預測精度比應用于BACT機翼時略有下降，其主要原因在于氣動非線性更加顯著.

值得指出的是，在本研究中采用blended mesh方法來簡化舵面偏轉時的流場網格生成和計算.由于舵面偏轉后流場網格生成依賴于網格變形程序，對大長細比導彈，舵面偏轉角度最大值可達8?左右，優化網格和網格變形程序能夠增加最大可偏轉角度，但在大角度舵面偏轉算例中無法完全代替嵌套網格等方法.

此外值得關注以下兩方面工作：一是改變降階模型的數學形式或辨識方法，以提高其應用于復雜氣動外形模型的精度；二是根據所設計的氣動彈性降階模型進行主動控制器設計.

致謝 感謝張冬云在導彈模型的氣動力網格生成方面給予有價值的建議；感謝陳志強在結構有限元建模方面提供的幫助.

1胡海巖,趙永輝,黃銳.飛機結構氣動彈性分析與控制研究.力學學報,2016,48(1)：1-27(Hu Haiyan,Zhao Yonghui,Huang Rui.Studies on aeroelastic analysis and control of aircraft structures.ChineseJournalofTheoreticalandAppliedMechanics,2016,48(1)：1-27(in Chinese))

2陳桂彬,鄒叢青,楊超.氣動彈性設計基礎.北京：北京航空航天大學出版社,2004(Chen Guibin,Zou Congqing,Yang Chao.Fundamentals of Aeroelastic Design.Beijing：Press of Beijing University of Aeronautics and Astronautics,2004(in Chinese))

3 Bismarck-Nasr MN.Kernel function occurring in subsonic unsteady potential fl w.AIAA Journal,1991,29(6)：878-879

4 Rodden WP,Taylor PF,McIntosh SC.Further refinemen of the subsonic doublet-lattice method.Journal of Aircraft,1998,35(5)：720-727

5 Liu F,Cai J,Zhu Y,et al.Calculation of wing flutte by a coupled fluid-structur method.Journal of Aircraft,2001,38(2)：334-342

6 Marques FD,Anderson J.Identificatio and prediction of unsteady transonic aerodynamic loads by multi-layer functionals.Journal of Fluids and Structures,2001,15(1)：83-106

7 Hall KC,Thomas JP,Dowell EH.Proper orthogonal decomposition technique for transonic unsteady aerodynamic fl ws.AIAA Journal,2000,38(10)：1853-1862

8 Xie D,Xu M,Dowell EH.Proper orthogonal decomposition reduced-order model for nonlinear aeroelastic oscillations.AIAA Journal,2014,52(2)：229-241

9 Liu Haojie,Hu Haiyan,Zhao Yonghui,et al.Efficient reduced-order modeling of unsteady aerodynamics robust to fligh parameter variations.Journal of Fluids and Structures,2014,49(8)：728-741

10 Mannarino A,Mantegazza P.Nonlinear aeroelastic reduced order modeling by recurrent neural networks.Journal of Fluids and Structures,2014,48：103-121

11 Zhang Weiwei,Wang Bobin,Ye Zhengyin,et al.Efficient method for limit cycle flutte analysis based on nonlinear aerodynamic reduced-order models.AIAA Journal,2012,50(5)：1019-1028

12陳剛,徐敏,陳士櫓.基于Volterra級數的非線性非定常氣動力降階模型.宇航學報,2009,25(5)：492-495(Chen Gang,Xu Min,Chen Shilu.Reduced-order model based on volterra series in nonlinear unsteady aerodynamics.Journal of Astronautics,2009,25(5)：492-495(in Chinese))

13陳剛,李躍明.非定常流場降階模型及應用研究進展與展望.力學進展,2011,41(6)：686-701(Chen Gang,Li Yueming.Advances and prospects of the reduced order model for unsteady fl w and its application.Advances in Mechanics,2011,41(6)：686-701(in Chinese))

14 Wu Zhigang,Chu Longfei,Yuan Ruizhi,et al.Studies on aeroservoelasticity semi-physical simulation test for missiles. Science China Technological Sciences,2012,55(9)：2482-2488

15楊超,吳志剛.導彈氣動伺服彈性穩定性分析.飛行力學,2000,18(4)：1-5(Yang Chao,Wu Zhigang.Aeroservoelastic stability of missile.Flight Dynamics,2000,18(4)：1-5(in Chinese))

16吳志剛,楊超.彈性導彈的連續與離散陣風響應.北京航空航天大學學報,2007,33(2)：136-140(Wu Zhigang,Yang Chao.Continuous and discrete gust responses of elastic missiles.Journal of Beijing University of Aeronautics and Astronautics,2007,33(2)：136-140(in Chinese))

17全景閣,葉正寅,張偉偉.軸向載荷對大長細比導彈穩定性的影響研究.兵工學報,2015,36(1)：94-102(Quan Jingge,Ye Zhengyin,Zhang Weiwei.Analysis on stability of a slender missile under axial loads.Acta Armamentarii,2015,36(1)：94-102(in Chinese))

18 Huang Rui,Li Hongkun,Hu Haiyan,et al.Open/closed-loop aeroservoelastic predictions via nonlinear,reduced-order aerodynamic models.AIAA Journal,2015,53(7)：1812-1824

19 Chiuso A,Picci G.Consistency analysis of some closed-loop subspace identificatio methods.Automatica,2005,41(3)：377-391

20 Chiuso A.The role of vector autoregressive modeling in predictorbased subspace identification Automatica,2007,43(6)：1034-1048

21 Houtzager I,Wingerden JW,Verhaegen M.Recursive predictorbased subspace identificatio with application to the real-time closed-loop tracking of flutte.IEEE Transactions on Control Systems Technology,2012,20(4)：934-949

22 Mor′e JJ.The Levenberg-Marquardt algorithm：implementation and theory//Numerical analysis.Berlin Heidelberg：Springer,1978：105-116

23 Waszak MR.Modeling the benchmark active control technology wind-tunnel model for application to flutte suppression.AIAA Paper,1996,3437

24 McNamara JJ,Friedmann PP.Flutter boundary identificatio for time-domain computational aeroelasticity.AIAA Journal,2007,45(7)：1546-1555

25 Borglund D,Ringertz U.Efficient computation of robust flutte boundaries using the mu-k method.Journal of Aircraft,2006,43(6)：1763-1769

26 Guruswamy GP.Frequency domain flutte boundary computations using Navier-Stokes equations on superclusters.Journal of Aircraft,2014,51(5)：1640-1642

27張偉偉,王博斌,葉正寅.跨音速極限環型顫振的高效數值分析方法.力學學報,2010,42(6)：1023-1033(Zhang Weiwei,Wang Bobin,YeZhengyin.HighefficientnumericalmethodforLCOanalysis in transonic fl w.Chinese Journal of Theoretical and Applied Mechanics,2010,42(6)：1023-1033(in Chinese))

28 Denegri CM.Limit cycle oscillation fligh test results of a fighte with external stores.Journal of Aircraft,2000,37(5)：761-769

29 Thomas JP,Dowell EH,Hall KC.Modeling viscous transonic limit cycle oscillation behavior using a harmonic balance approach.Journal of Aircraft,2004,41(6)：1266-1274

30 Chen YM,Liu JK,Meng G.Equivalent damping of aeroelastic system of an airfoil with cubic sti ff ness.Journal of Fluids and Structures,2011,27(8)：1447-1454

31 Cui Peng,Han Jinglong.Numerical investigation of the e ff ects of structural geometric and material nonlinearities on limit-cycle oscillation of a cropped delta wing.Journal of Fluids and Structures,2011,27(4)：611-622

32 Stanford B,Beran P.Direct flutte and limit cycle computations of highly fl xible wings for efficient analysis and optimization.Journal of Fluids and Structures,2013,36(1)：111-123

AEROELASTIC MODEL OF REDUCED-ORDER FOR A SLENDER MISSILE1)

Yang Zhijun?Huang Rui?Liu Haojie?Zhao Yonghui?Hu Haiyan?,2)Wang Le??(College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)?(China Academy of Launch Vehicle Technology，Beijing 100076，China)

In the design phase of slender missiles,it is essential to predict their aeroelastic/aeroservoelastic behaviors accurately.The accurate prediction,however,is faced with the tough problem of CFD for the aerodynamic loads on slender missiles.How to establish the aerodynamic models of reduced-order is the key technology to break through the bottleneck in the transonic aeroelastic analysis and control of the slender missiles.Although the aerodynamic reducedorder methods have made important progress in predicting the aerodynamic loads and aeroelastic response of the twodimensional airfoil,still there are few research reports about the aerodynamic reduced-order models of the more complex airplane models.In this study,the recursive Wiener model of reduced-order is constructed for the aerodynamic loads on a slendermissileaccordingtothetrainingdataofCFD,whiletheparameters ofthemodelcanbeestimatedviathepredictorbased subspace identificatio algorithm and Levenberg-Marquardt algorithm.The recursive Wiener model of reducedorder can be integrated with the finit element model of the missile structure so that the aeroelastic/aeroservoelastic model of reduced-order is established for the missile.The accuracy of the aeroelastic models of reduced-order is tested under di ff erent Mach number in the numerical simulations.The numerical simulations show that the aeroelastic modelsof reduced-order can accurately predict the unsteady aerodynamic loads and the aeroservoelastic frequency response of the slender missile model under di ff erent fligh conditions.

slender missile,aerodynamic model of reduced-order,recursive Wiener model,flutte boundary,limit cycle flutte

V211,V215.3

：A

10.6052/0459-1879-16-358

2016–11–30 收稿，2017–03–20 錄用,2017–03–21 網絡版發表.

1)國家自然科學基金(11502106),航空科學基金(2015ZA52),江蘇省自然科學基金(BK20150736)和江蘇省普通高校研究生科研創新計劃(KYLX15-0251)資助項目.

2)胡海巖,中國科學院院士,教授,主要研究方向：飛行器結構動力學與控制.E-mail：hhyae@nuaa.edu.cn

楊執鈞,黃銳,劉豪杰,趙永輝,胡海巖,王樂.大長細比導彈的氣動彈性降階模型.力學學報,2017,49(3)：517-527

Yang Zhijun,Huang Rui,Liu Haojie,Zhao Yonghui,Hu Haiyan,Wang Le.Aeroelastic model of reduced-order for a slender missile.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：517-527