基于復合多層 RBF網絡的組合預測的研究
——以商業銀行農村信貸為例

盛國敏，莊 健

（1.中國農業銀行 天長市支行，安徽 天長 239300；2.安徽工業大學 商學院，安徽 馬鞍山 243000）

基于復合多層 RBF網絡的組合預測的研究
——以商業銀行農村信貸為例

盛國敏1，莊 健2

（1.中國農業銀行 天長市支行，安徽 天長 239300；2.安徽工業大學 商學院，安徽 馬鞍山 243000）

為了解決多元線性回歸和 logistic 回歸在預測中的精度不高問題，運用組合預測的思想，提出通過開發運用復合多層 RBF 神經網絡將多元線性回歸和 logistic 回歸組合的預測方法，并應用于商業銀行的個人信用評估中，其結果表明組合預測方法能夠獲得比單層 RBF 網絡法和單一回歸方法更高的預測精度。

多元線性回歸；logistic 回歸；復合多層 RBF 神經網絡；組合預測；個人信用評估

信用伴隨人們一生，是一生積累的信任度和誠信度的體現。在商品交換等經濟活動中，它是一種價值的運動，是整個市場經濟發展的基石。 在我國，信用已經是人們立信他人的基礎，是社會經濟活動的“身份證”。 我國信用基礎建設發展緩慢，尤其是個人信用額度預測體系建設很不完善，失信違約事件時常發生已成為當前市場經濟發展的基本特征，阻礙著我國消費經濟的快速發展。

在 很 多 發 達 國 家 中 ，個 人 信 用 評 估 方 法[1]已 經 發展到成熟地步。除各種統計方法外，人工智能技術如神經網絡、專家系統、分類樹以及遺傳算法也得到了廣泛的重視。雖然現在已經有很多高新技術工具和各類軟件在商業經濟中加以使用，但是由于我國個人信用體系建設的較晚，已有的信用評價機制發展相對落后，在評估方法的精確度方面不盡人意。因此本文試圖通過構建新的復合多層 RBF 神經網絡來評估個人信用，為解決上述問題進行的嘗試。

徑 向 基 函 數 網 絡[2]是 一 種 性 能 優 良 的 前 饋 型 網絡，具有不存在局部最優解和學習速度快的優點，因此被廣泛應用到各個領域。徑向基函數網絡自提出以后，發展了許多算法，這些算法大都旨在改進中心的選取，寬度系數的確定，徑向基函數個數的確定方法 和減少 計 算量，具 體 見文獻[3-8]。

1 模型構建原理

個人信用評估可以被看作是模型識別中的異類分類問題——通過歷史上不同類別的 （信用好和信用不好）的若干樣本，從調研的樣本中提取、分析其規律，建立數學模型，然后用于新樣本的判斷。 直觀地說，就是將個人信用的評估轉化為各種指標體系的量化問題——貸款申請者最后能否還本付息取決于其個人基本的經濟和信用狀況。目前個人信用評價機制主要有多元判別分析法等數學模型方法和神經網絡法等人工智能方法。

從總體上說，這些模型均可以統一為分類問題，就是按照歷史數據建立判別模式，將新的需要分類的樣本數據代入，得到一個輸出值，從而確定樣本的分類。這些方法可以說是信用評估過程中的主流方法，得到了廣泛的應用，但應該說不同的方法都存在一定的問題，如多元判別分析模型是根據特定樣本數據建立的，一個地方建立的模型不一定適合其他地方，還要求樣本滿足正態分布、協方差等過于嚴格的前提條件，并且模型有用性比較差。 而 RBF 神經網絡也存在隱層神經元個數難以確定，各層核函數的中心不能很好分配在恰當的位置上等問題。從信息論的角度來看，每一種預測方法都包含其特殊的信息，即便是相對比較差的預測方法，也一定會包含著其他的方法所不具有的獨特信息。因此，為了盡可能多的利用全部有效信息，可以采用一定的方法和手段對不同的方法進行組合，這就是所謂的組合預測[9]。

這里選取個人信用評估過程中應用比較成熟、效果比較明顯的線性回歸和 logistic 回歸方法，通過基于復合多層 RBF 神經網絡構建的組合預測模型，希望將復合多層 RBF 神經網絡的高精度和線性回歸、logistic 回歸方法的高穩健性有效結合，并克服各自的缺點。

1.1 多層 RBF 網絡中的聚類算法

構建第一層的輸出網絡。程序中輸入樣本X為

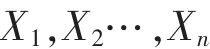
和它們所對應的期望輸出值是

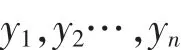
做增廣樣本為

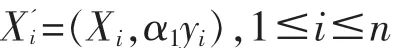
這里 α1＞0。 再用 K-mean 法將

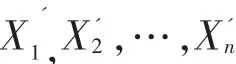
分成 m1個聚類

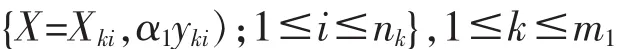
這樣得到 m1個樣本聚類

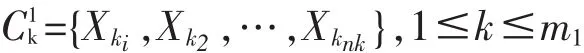
把每個聚類的均值作為聚類中心，即

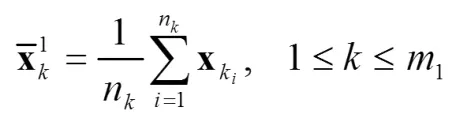
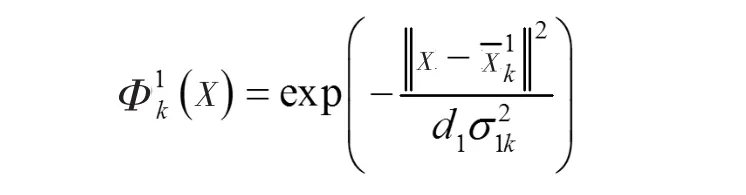
于是網絡第一層表達式為

這里

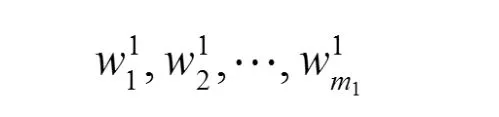
表示權重，使用最小二乘法計算，使下列擬合殘差平方和

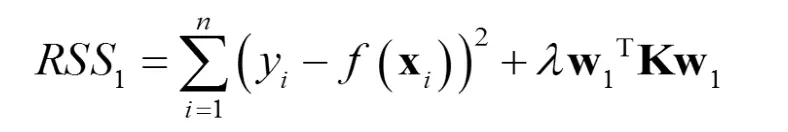
聚類時，我們采用了增廣樣本。這樣得到的聚類

其中包含我們期望輸出的信息，可以得到采用增廣樣本的徑向基函數網絡的精度高很多。 α1的取值不同，得到的聚類不同，網絡的精度也不同，所以 α1也是一個需要優化的參數。

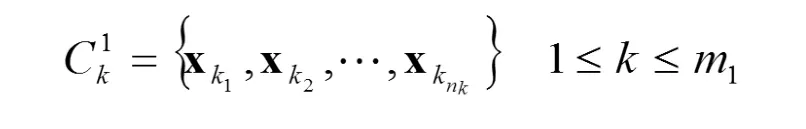
構建第二層的輸出網絡。首先計算第一層網絡的擬合誤差

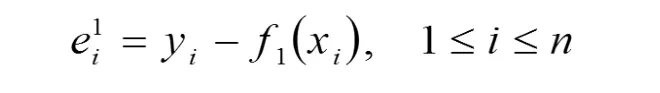
然后把輸入樣本與前一層的誤差項組合在一起，得到增廣樣本

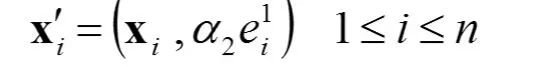
這里 α2＞1。

然后再用 K-mean 法將

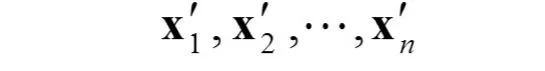
分成 m2個聚類

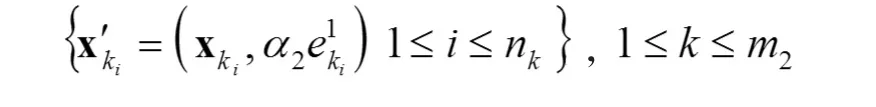
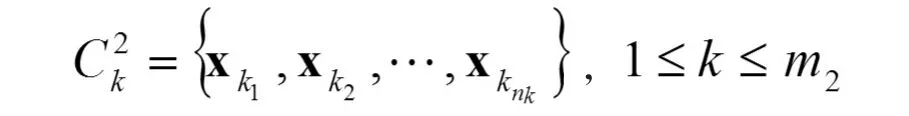
再 令 寬 度 系 數 為 d1， 其 中為 聚 類的 樣 本 方差，而 d2是有待優化的參數。

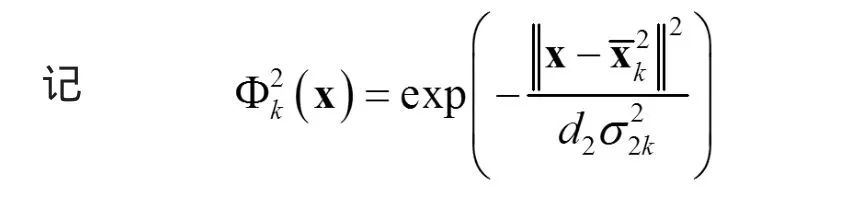
于是第二層網絡的輸出函數為

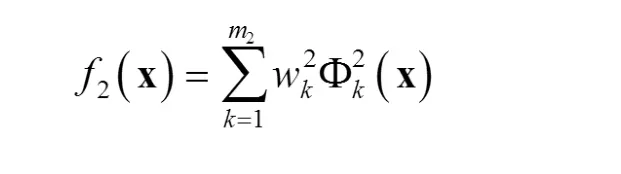
各個聚類的中心為

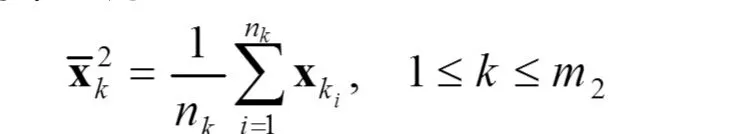
這樣得到了 m2個新的樣本聚類

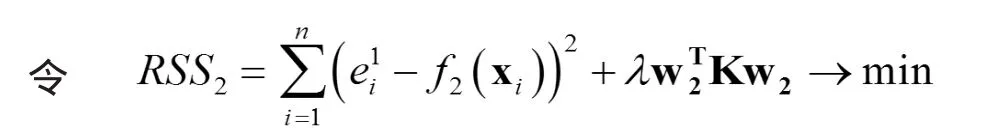
可以得到第二層網絡的加權系數的值。 若取 λ=0，則 W2為普通最小二乘法；若取 λ＞0，則 W2為正則最小二乘法。

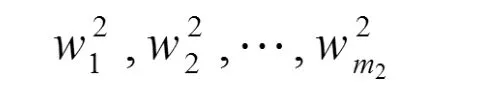
這樣得到了一個更精確的模型

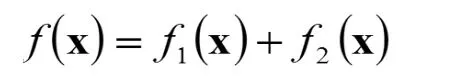
需要說明的是，在增廣樣本

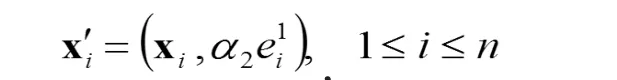
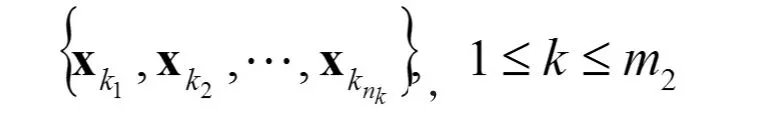
受到擬合殘差的影響就小，所得到的函數 f2（X）對殘差的抵消作用就小。 α2也是要優化的。

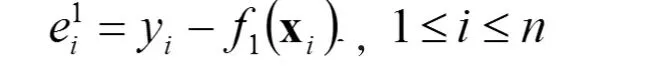
循環往復計算每一層網絡，把每一層網絡相加，最后可以構建一個高精度的徑向基函數神經網絡。

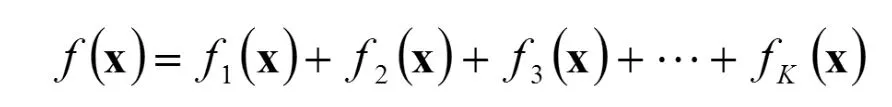
1.2 復合多層 RBF 網絡構建原理

在上述聚類算法中，函數在每一個聚類上的值用一個徑向基函數來逼近。這樣網絡的逼近精度是有局限的。 于是，做出改進，將一個聚類中的每個樣本都看成一個徑向基函數的中心，一個樣本對應一個徑向基函數。對每個聚類，我們構建一個子 RBF 網絡，每個徑向基函數的中心就是這個聚類中樣本。

設 Ck是一個聚類，Ck中的樣本記為

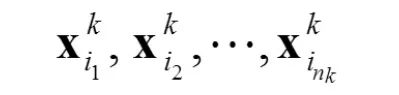
于是這個子 RBF網絡為

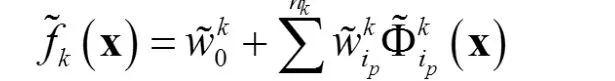
其中

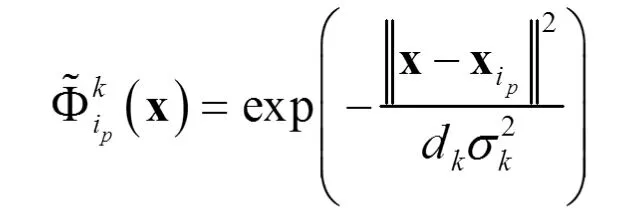
記權重向量為

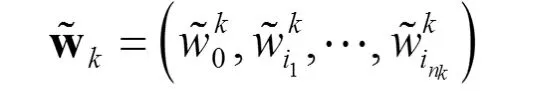
定義殘差平方和

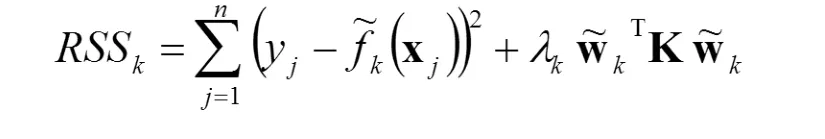
若 λk＞0，則得正則最小二乘解

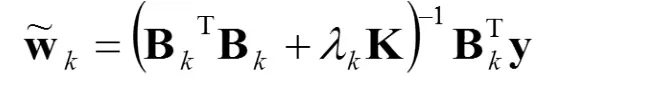
若令 λk=0，采用廣義逆矩陣法，得最小二乘解

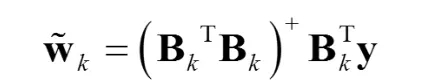
其中

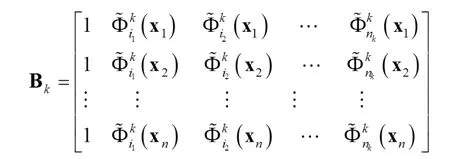
子網絡的 GCV 計算公式如下：

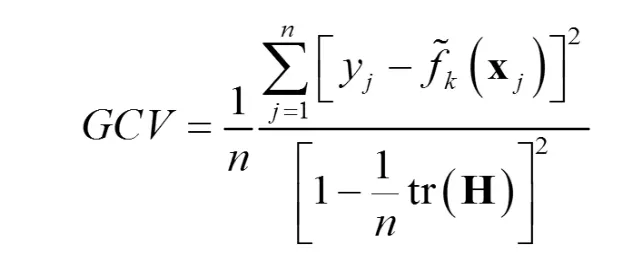
其中，

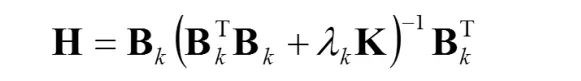
子網絡的參數 dk和 ap的優化是使 GCV 最小。

再把得到的所有這些子網絡整合起來。設共有K個子網絡，整個網絡就是輸出的加權和

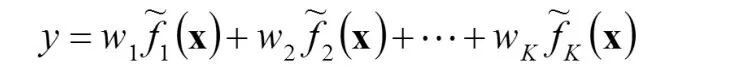
當 X取遍所有的樣本時，得到

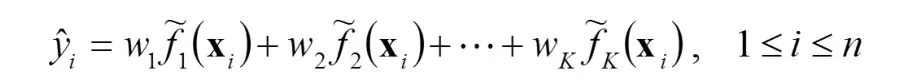
令

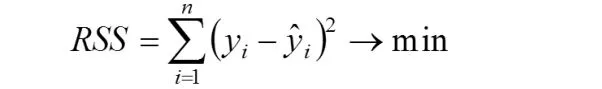
于是就得到了 的最小二乘解，

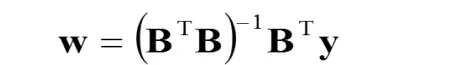
這樣整個網絡構建完畢。

2 變量和樣本數據的選取

文中選取的輸入變量包括 10 項， 用 xi表示；輸出變量 1 項，用 y 表示。 具體如表 1。

文中采用某商業銀行的個人貸款數據。為保證數據的普遍性進行再選擇，目的是調整 y=0 和 y=1的數據選擇比例。由于整體樣本數據數量大，數據結構比較多樣，差異比較大，因此采取分層抽樣的方法，先依照是否給予貸款將整體分成為兩份，然后從每一組中隨機抽取 400 個樣本， 從而使兩者之比近似為 1∶1。 最終得到 850 個數據，其中訓練學習數據包括 420 個樣本；其余 430 個樣本構成檢驗數據，用于單一模型的訓練學習和檢驗。最后用單一模型的結果計算作為組合模型的輸入變量。

表1 輸入變量和輸出變量

3 模型的構建

3.1 多元線性規劃模型

建立因變量y 對自變量 xi的線性回歸模型方程為：

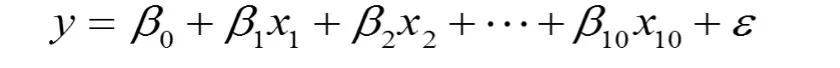
在建立理論回歸模型方程后，利用已有的訓練數據，使用 Stata 軟件進行計算。 在本文中，采用顯著性逐級檢驗分析進行多元線性回歸分析，結果自變量x1，x3，x6，x9通過了顯著性檢驗，得到的回歸方程為：

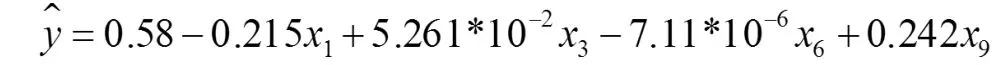
從上述模型可以看出，能否獲得貸款y與模型中自變量 x1，x3，x6，x9聯系相對較大。 并且通過方程可以看出與自變量 x3，x9為正線性相關的關系；與x1，x6，為負線性相關的關系。 通過 Stata 統計軟件中的 z檢驗和 t檢驗對方程的系數和方程整體的顯著性進行檢驗，結果均顯著成立，表明方程建立成功。

3.2 Logistic 回歸模型

建 立因變 量 y 對自 變量 xi的 logistic 回歸模型方程為：

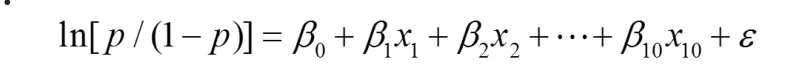
從模型可以看出：貸款能否取得y也是與模型中的自變量 x1，x3，x6，x9聯系相對較大。 該模型的樣本決定系數 R2為 0.82，取得了很好的擬合效果。

3.3 復合多層 RBF 網絡組合模型

組合模型的基本原理如下：

yt（t=1，2， … ，n） 表 示 實 際 觀 察 值 ；yit（i=1，2， … ，m；t=1，2，… n）表 示 第 i 種 方 法 的 預 測 值 ；則 eit=yt-yit（i=1，2，…m；t=1，2，…n）表示第 i種預測方法對第 t個數據進行預測時的誤差。

若用m種方法進行組合預測，設各預測方法的系數分別為 k1，k2，…，km，km，滿足

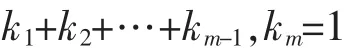
本文中把誤差平方和 RSS 最小作為評定組合預測模型最優的標準，既求 k1，k2，…，km-1，km，使取得最小值。 其中均方根誤差 RMSE，平均絕對誤差MAE也在本文中列出作為比較。 根據多元函數求極值的方法，用 Q 分別對（i=1,2,…,m）求導，求 得駐點（使取得極小值的點）。 再加上限制方程 k1+ k2+…+km-1，km=1。 就可解得的 k1，k2，…，km-1，km。

本文選定神經網絡核函數第一層個數為 40，以后各層為 120 個。 在訓練的過程中依據網絡層數從少到多的變化，觀察誤差的變化，學習速率會很明顯的優于單層徑向基函數網絡。 在復合多層 RBF 網絡設計的過程中，關鍵是增加網絡層數。隨著徑向基函數網絡層數的不斷增加，每一層網絡對前一層網絡的誤差進行擬合，這樣使得神經網絡的誤差降到一定的程度，最終使得多元實函數和 Logstic 模型組合預測的步長和精度大大提高。 當預測步長達到 32時，預測誤差超過控制線 0.03。 本文訓練的誤差變化情況如圖1。

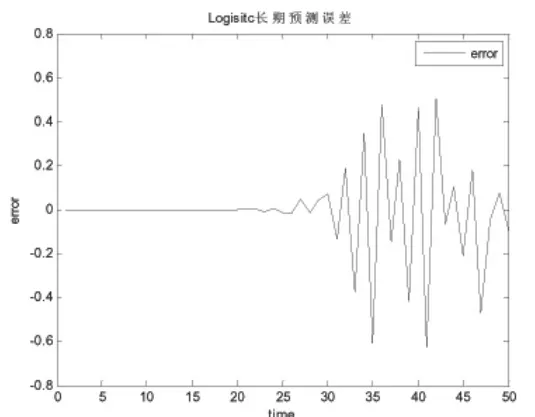
圖1 復合多層 RBF神經網絡訓練誤差曲線

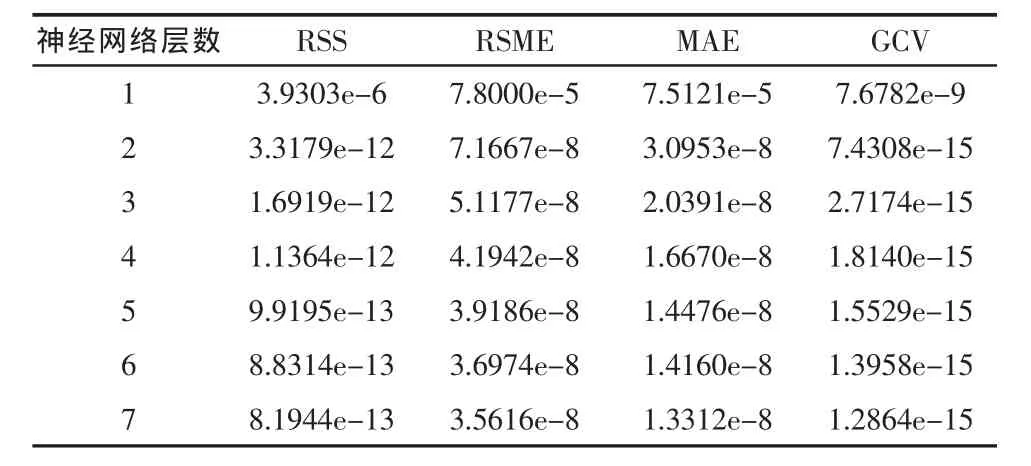
表2 復合多層 RBF網絡每一層的訓練誤差

表3 復合多層 RBF網絡的預測結果

由表2和表3可知，復合多層徑向基函數網絡的訓練層數達到 7 層，訓練誤差達到 8.1944e-13，預測誤差達到 7.8981e-14，實現了訓練的目的。

4 結果分析

通過構建的復合多層徑向基函數網絡，對預測精度的比較，來評價所構建的3個個人信用評估模型。 為了保持數據的一致性，本文選擇 3個模型中均使用的后 430 個，模型的預測結果作為評定的基礎。需要說明的是前2種方法在判定貸款者的類型的時候，是以 0.5 作為臨界值的，即將預測值大于等于 0.5稱為信用好，反之則認為信用不好。比較結果見表 4。

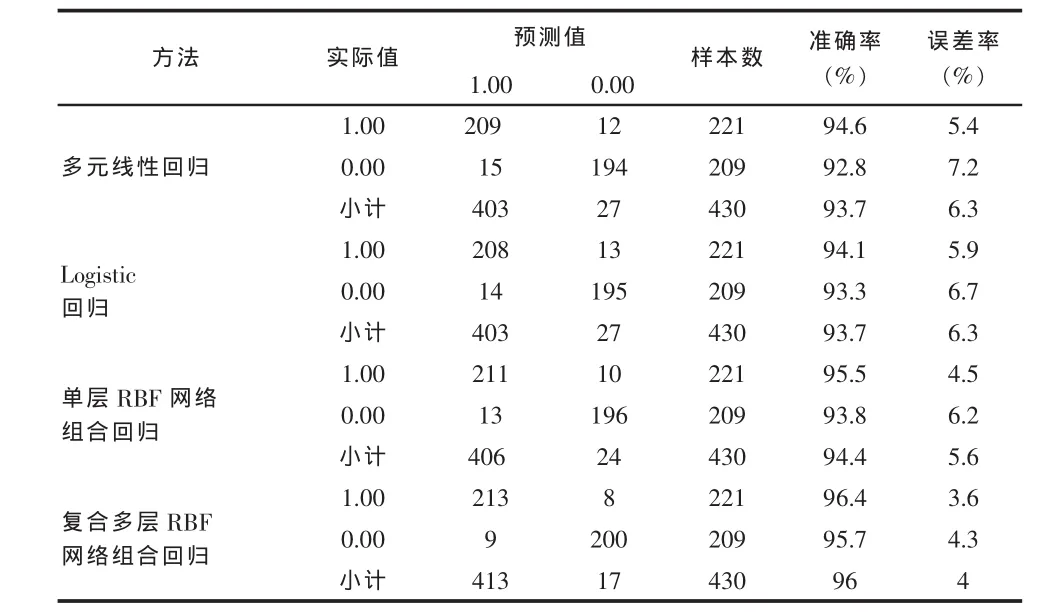
表4 3種個人信用評估方法的預測精度的比較

由表4可以看出，基于復合多層徑向基函數網絡的多元線性回歸和 Logistic 回歸的組合預測模型，預測準確率遠比2個單一模型的準確率高很多。在實際操作過程中，要盡量避免將無法按期償還貸款者當成能夠按期償還貸款者發放貸款，這樣會導致壞賬的形成。復合多層徑向基函數網絡組合預測模型將犯此錯誤的概率由多元線性回歸模型的 7.2%和 Logistic 回歸模型的 6.7%和單層徑向基函數網絡組合模型的 6.2%，降低到 4.3%。 這在實際操作過程中規避信用風險具有更大的實際意義。

上述結果足以表明，復合多層徑向基函數網絡組合預測模型，更加優于多元線性回歸和 Logistic 回歸模型，組合預測可以作為個人信用評估的可供選擇的更為精確的方法。

[1]石慶焱，靳云匯．多種個人信用評分模型在中國應用的比較研究[J]．統計研究，2004,20（6）：43-47．

[2]Moody J,Darken C.Fast learning in networks of locallytuned processing units.Neural Computation[J].1989，16（1）: 281-294.

[3]Chen S,Cowan CFN.and Grant PM.Orthogonal least squares learning algorithm for radial basis function networks[J].IEEE Transactions on Neural Networks,1991,2（2）:302-309.

[4]Chen S，Cheng ES,Ai Kadhimi,K.Regularized least squares learning algorithm for constructing radial basis function networks [J].International Journal of Control,1996，64 （5）：829-837.

[5]Guang-bin H,Saratchandran P,Sundararajan N.A generalized growing and pruning RBF （GGAP-RBF）neural network for function approximation [J].IEEE Transactionson Neural Network,2005,16（1）:57-67.

[6]Broomhead DS,Lowe D.Multi-variable functional interpolation and adaptive networks.[J].Complex System,1988,2（2）: 321-335.

[7]王凌,鄭大鐘.徑向基 函數神經網 絡 結 構 的 混 合 優 化 策 略[J].清華大學學報：自然科學版，1999，39（7）：50-53.

[8]陳政,楊天奇．基于 RBF 神經網絡的股票市場預 測[J].計算 機應用與軟件，2010，27（6）：108-110.

[9]王春峰，萬海暉，張維．組合預測在商業銀行信用風險評估中的應用[J]．管理工程學報，1999，13（1）：5-10．

責任編輯：胡德明

Research on Composite Prediction Based on Composite Multilayer RBF Neural Network——Taking Rural Credit in Commercial Banks As an Example

Sheng Guomin1,Zhuang Jian2
(1.Tianchang Branch,Agricultural Bank of China,Tianchang 239300,China; 2.School of Business,Anhui University of Technology,Ma'anshan 243032,China)

For solving the problem that the multiple linear regression and logistic regression are not highly accurate in prediction and with the idea of combination prediction,the prediction method of combining multivariate linear regression and logistic regression by developing and using composite multi-layer RBF neural network is proposed and applied to personal credit evaluation of commercial banks.The results show that the combination forecasting method can obtain higher prediction accuracy than single RBF network method and regression method.

multiple linear regression;logistic regression;compound multilayer RBF neural network; combination forecasting;personal credit evaluation

O241

：A

：1672-447X(2017）03-0014-05

2016-12-28

盛國敏（1989-），安徽天長人，中國農業銀行安徽滁州天長市支行經濟師，研究方向為機器學習及應用；

莊健（1957-），上海人，安徽工業大學商學院博士研究員，研究方向為機器學習。