無線信道指紋特征識別技術研究

張雷+王軍

摘 要： 無線信號識別在無線信號傳輸和監測中占有重要地位，為了減少各類干擾源和白噪聲對傳播信號造成的影響，提高信號識別準確度，分析了基于PCA和小波變換法的特征提取技術，提出積分包絡法來提取接收信號特征的模型，采用不同信號樣本包絡之間的貼近度構建簡潔而明確的評價指標以驗證有效性，同時利用模糊數學識別功能計算樣本與區域劃分之間的貼近度，通過貼近度差值來判斷和識別無線信號。實驗結果表明，該算法識別性能較好，不僅具有較高的識別率和良好的穩健性且計算復雜度較低。

關鍵詞： 積分包絡； 模糊數學； 小波變換； 貼近度

中圖分類號： TN92?34 文獻標識碼： A 文章編號： 1004?373X（2017）13?0013?04

Abstract： The wireless signal recognition plays a crucial role in the wireless signal transmission and monitoring. In order to reduce the effect of various interference sources and white noise on transmission signal， and improve the signal recognition accuracy， a feature extraction technology based on principal component analysis （PCA） and wavelet transform method is analyzed， and a model to extract the characteristics of received signal with integral envelope method is proposed. The close degree among the envelopes of different signal samples is used to construct the concise and specific evaluation indexes， and verify its validity. The fuzzy mathematics identification function is used to calculate the close degree between the sample and regional division. The wireless signal is judged and identified according to the difference value of the close degree. The experimental results show that the algorithm has high recognition performance， high recognition rate， perfect robustness， and low computational complexity.

Keywords： integral envelope； fuzzy mathematics； wavelet transform； close degree

0 引 言

移動通信產業的迅猛發展極大的改變了世界，已成為世界發展的主要高科技產業之一，對人類社會產生了巨大的影響，為人們的生活帶來了便利，同時也為信號監測和提取提出了新的挑戰。無線信道的傳輸是在一個相對比較復雜的環境下開展的，所以提取無線信道中的信號相關特征具有重大的研究價值，在無線通信領域，最重要的內容就是探討無線信道。在無線通信信道中，信號的發射端和接收端之間電磁波傳播受到建筑等障礙物的反射、折射、衍射以及它們的聯合作用干擾，導致信號的不同頻率分量存在著不同程度的時延[1]。

本文基于離散時間信號中各參數的時變特性，比較了積分包絡法、PCA主成分分析法和小波變換法提取接收信號的特征。通過積分包絡法獲取的信號包絡值最能夠凸顯信號的特性，引入包絡相關系數的計算公式，檢驗了包絡值作為“指紋”特征的合理性。同時，構建不同信號樣本包絡之間的貼近度作為樣本歸類的評價指標，通過計算信號樣本的包絡平均值和方差，利用模糊數學理論求取信號樣本包絡與不同場景包絡之間貼近度函數值，選取能代表其規律性的一段數據進行貼近度計算，找出了相同的信號源[2]。

1 特征提取模型建立

由于接收的實際信號幅值與時間間隔和頻率有關，在每個樣點中各樣本數據的時間間隔一致下。文中首先討論了PCA主成分分析算法和小波變換算法兩類特征提取算法，分析了兩者的不足之處，提出用積分包絡法來提取信號特征的算法。

1.1 基于PCA的特征提取

假設為維向量，協方差矩陣為主成分分析就是把這維向量降到維向量滿足其中，為如下變換矩陣：

如上所述，求解第1個主分量其數學實質就是在的條件下，尋求向量使得達到最大值。設相應的標準正交特征向量為則存在正交矩陣使得：

假定向量為維單位向量，則有：

從以上分析得到，當即時方差最大為，同理可得其他主分量（實際應用中只選取前個主分量）分別為：

對于PCA算法，雖然該方法操作簡單、客觀性較強，但由于算法中涉及到特征向量，所以對題目中的大量信號數據進行PCA特征提取，必然會產生數量龐大的特征向量，極大地降低了算法的效率。

1.2 基于小波變換的特征提取

小波變換是一種信號的視頻局域化分析方法，分析窗口大小固定，但形狀、時間窗和頻率窗都可以改變，而且在時間域和頻率域都有表征信號局部特征的能力[3]。小波變換具有多分辨率分析的特點，因此在提取信號源暫態特征時應用較廣泛。離散小波變換可表示為小波函數與采樣信號的內積[4]，即：

式中：為采樣信號；為尺度參數；為平移參數；為離散小波函數，且滿足：

雖然在輻射源差別很小的情況下，小波分析也能通過增加分解層次體現個性差異，但同時也會使計算量和特征空間維數增加，而且可能存在冗余和無效特征。因此，通常需要搜尋原始特征集中最優特征子集。借鑒二重結構編碼的遺傳算法給出以下最優特征子集的評價準則。

首先定義特征集合空間的可分離度為其計算公式如下：

式中：為第個樣本的歸一化標準差，且為維樣本點的第類樣本的核心；為第類樣本的第維樣本點的核心；為極差，用于歸一化樣本的維信息。

假設待識別的信號有類，特征選擇的評價準則函數定義如下：

在挑選出分辨能力強的特征后，利用支持向量機分類器便可以實現對信號的個體識別。

小波分析特征提取的結果不僅與分層數密切相關，同時還受權重因子的影響。目前，對于分層數的確定仍然沒有現成的方法可供借鑒。此外，權重因子受主觀因素的影響過大，導致特征提取結果客觀性較差。所以，在此使用小波分析法提取信號特征值不恰當。

1.3 基于積分包絡的特征提取

假設接收端接收的實際信號為：

式中：為信號包絡特性函數，取決于信號能量變化情況；為載波信號包絡；為載頻；為載波相位；為高斯白噪聲。因此，信號和噪聲的合成包絡為：

式中為噪聲包絡。

一般情況下，由于存在不同發射端和噪聲等因素的影響，信號峰值會有所不同。為了方便比較，往往會對采集到的信號數據進行歸一化處理。

積分包絡是對信號積分后取的包絡。經積分包絡變換后的暫態信號波形會有較大差異。對于平穩信號：

可以認為在時間內是不變的。假設對積分，可得其積分包絡從式（8）可以看出，積分后的包絡與積分時間間隔、信號頻率有關。由于積分時間間隔不變，且平穩信號的頻率也不變，因此，原包絡恒定的平穩信號經過積分后也是恒定的平穩信號。不同頻率的信號經過積分后的包絡是不同的，故信號的積分在一定程度上能反映信號頻率的變化。以下對非平穩信號進行積分包絡，假設任意非平穩信號在很小的時間內為線性調頻信號：

可以認為在時間內是不變的。假設對積分，得到積分包絡

得出包絡值后，可以根據采樣段的信號作出初始信號圖和信號包絡圖。

積分包絡算法是直接針對原始數據進行特征提取，充分還原原始數據的特征。同時，積分包絡算法操作性簡單、數據量小的特點也極大地提高了算法的求解效率。

1.4 指紋“特征”合理性檢驗方法

檢驗“指紋”特征的合理性，其實質就是檢驗以該特征為標準是否能夠將不同場景進行合理的區分。可以通過計算不同場景包絡值之間的相關系數對以包絡值作為“指紋”特征的合理性進行檢驗。

記分別為場景的信號包絡，它們之間的協方差計算公式為：

求得場景與場景的相關系數為：

2 評價指標的確定

首先找到信道信號存在的周期性。取各場景中具有代表性的某100個樣點作為參考點。以下將通過模糊數學理論進行有效地識別。場景識別涉及到一維向量指標，因此可以用模糊多指標進行個體識別。首先，選取各樣點的包絡值序列作為評價指標，然后，采用多指標個體模糊識別的方法對場景進行識別。

可以假設各樣點包絡值均服從正態分布。如果將各樣點的包絡值分別看作是區間的模糊子集（稱之為正態模糊子集），那么對正態分布的密度函數稍加改造就可作為其隸屬函數：

式中為第個樣點的樣本變量。

為了對兩個未知類別的場景樣本進行識別，先定義包絡均值與模糊子集的貼近度如下：

式中表示的隸屬函數。

對于正態型模糊子集，由于，所以：

多指標個體識別遵從就近原則。

3 實驗結果與分析

通過軟件進行仿真實驗，本文模擬構造了三種場景的真實信道測量結果，根據積分包絡的特征提取方法繪制了三種場景的初始信號和包絡信號波形圖，如圖1～圖3所示。

通過計算不同場景包絡值之間的相關系數，對以包絡值作為“指紋”特征的合理性進行檢驗。計算結果得出，。結果表明，包絡特性用于分析驗證所建模“指紋”合理有效。

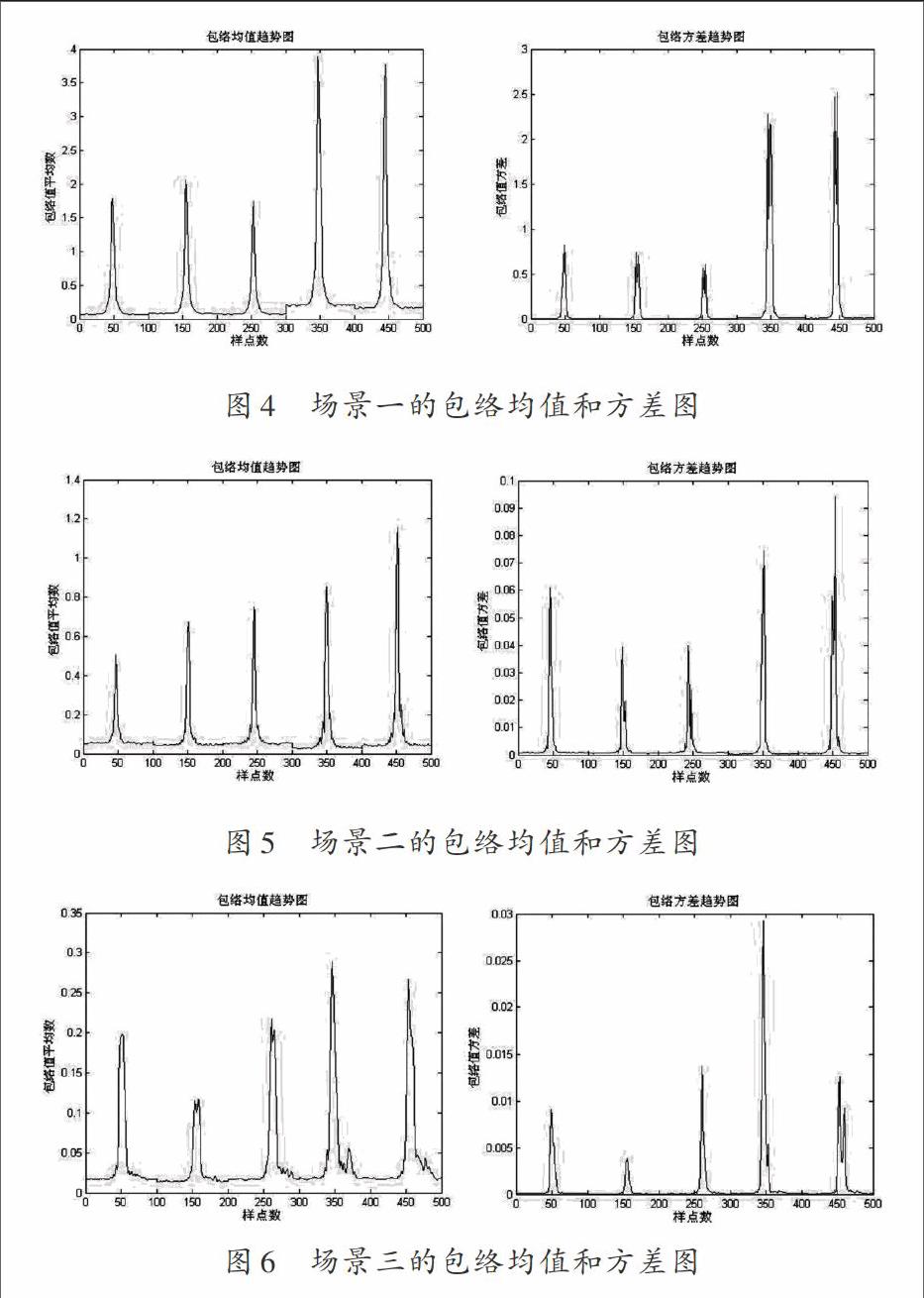
以不同樣本包絡值之間的貼近度作為識別采樣信號歸類的評價指標，求得樣本的包絡均值和方差趨勢圖，如圖4～圖6所示。

分析圖4～圖6可知，信道信號存在周期性，且周期為100 s左右。因此，取各場景中具有代表性的某100個樣點作為參考點。將未知類別的兩個信道數據，每個建立100項指標，分別是上的模糊子集。通過未知類別的兩個個體求得包絡均值和方差。計算對的貼近度可以得到由就近原則，應歸入場景一類。對的貼近度為由就近原則，應歸入場景一。

綜上分析，問題二中的兩個測試數據均屬于場景一。對歸類結果進行圖形描述，結果如圖7，圖8所示。

4 結 論

與PCA主成分分析法和小波變換法相比，通過積分包絡法獲取的信號包絡值最能夠凸顯信號的特性，能有效地將問題中的三種場景進行區分。為了檢驗包絡值作為“指紋”特征的合理性，引入了包絡相關系數的計算公式。計算結果表明，選取積分包絡值作為信道的“指紋”特征是合理的。

采取不同信號樣本包絡之間的貼近度作為樣本歸類的評價指標，計算出樣本的包絡平均值和方差。利用模糊數學理論求取信號樣本包絡與已知包絡之間貼近度函數值。選取各場景中能代表其規律性的一段數據進行貼近度計算。最后的計算結果表明，兩個采樣信號均與已知場景信號吻合。

參考文獻

[1] 錢玉文，宋華菊，孔建壽，等.一種基于網絡隱蔽時間信道的網絡指紋模型研究[J].兵工學報，2012，33（1）：19?25.

[2] 劉愛霞.雷達信號包絡的特征提取與分類[D].西安：西安電子科技大學，2003.

[3] 曹喆.一種區域特性的小波圖像融合新算法[J].計算機工程與應用，2011，47（26）：213?215.

[4] 陳韜偉，朱明，陳振興.雷達輻射源信號小波變換特征提取方法[J].計算機工程與應用，2010（6）：245?248.

[5] 辛焦麗，高麗.基于遺傳算法的蜂窩網絡接入信道動態分配方案的設計[J].現代電子技術，2016，39（15）：5?7.

[6] 陳慧玲.信號個體特征的檢測和識別技術研究[D].西安：西安電子科技大學，2013.

[7] 錢夢陽.信道參數提取方法研究[D].南京：南京郵電大學，2012.

[8] 柯志龍.基于幅頻特性的無線信道指紋研究[D].廈門：廈門大學，2011.

[9] 薛偉，王忠.基于實測的無線信道仿真分析[J].中國測試技術， 2008，34（1）：77?79.

[10] 張旭.基于信號分析的無線設備“指紋”特征提取[D].北京：北京郵電大學，2015.