基于小波的聲發射信號去噪研究

楊慧+顧菊平+華亮+羅來武+陳猛

摘 要： 由于小波變換具有較強的時頻分析和局部分析能力，常用于非平穩信號的去噪處理中。首先根據小波分解后各高頻系數所占的能量百分比對信號進行提純，再對提純后的信號進行小波閾值去噪，并運用信號能量百分比和頻譜分析對去噪效果進行評判。實驗結果表明，這種先提純后閾值去噪的處理方法能夠在保證信號不失真的前提下，有效去除聲發射信號中的噪聲。

關鍵詞： 小波閾值去噪； 信號提純； 頻譜分析； 去噪

中圖分類號： TN911.7?34； TB52 文獻標識碼： A 文章編號： 1004?373X（2017）13?0070?03

Abstract： The wavelet transform is widely used in the denoising of non?stationary signal due to its strong time?frequency analysis and local analysis abilities. The signal is purified according to the energy percentage of each high?frequency coefficient after wavelet decomposition， and then performed with wavelet threshold denoising. The signal energy percentage and frequency spectrum analysis are used to evaluate the denoising effect. The experimental results show that the method to conduct the purification before threshold denoising can eliminate the noise in the acoustic emission signal effectively while ensuring that the signal is undistorted.

Keywords： wavelet threshold denoising； signal purification； spectral analysis； denoising

0 引 言

在聲發射檢測中，采集到的聲發射信號不可避免地包含著由環境和儀器產生的噪聲，而噪聲的存在會對聲發射信號的特征提取、聲發射源定位等后續處理造成影響。所以對采集到的聲發射信號進行去噪是聲發射檢測中一個非常重要的步驟。尋求探索更完善、更有效的去噪方法可有力地推動聲發射檢測技術的發展與進步，具有非常重要的現實意義。

由于聲發射信號具有多樣性、時變性、非平穩性等特點，對分析方法的局部分析能力提出了較高要求，小波分析由于其具有較強的局部分析能力得到了廣泛應用。目前基于小波去噪技術的研究主要圍繞小波高頻系數的處理展開，通過抑制噪聲的小波系數或強化信號的小波系數實現去噪。根據信號處理的原理不同，主要分為小波變換模極大值法、小波系數尺度相關法和小波閾值去噪法三大類[1]。小波變換模極大值法能夠有效保留信號的奇異點，也無需知道噪聲的方差，但重構時計算速度比較慢，且尺度的不同對去噪效果影響較大；小波系數尺度相關法在信號邊緣特性分析方面有明顯優勢，但需要對噪聲的方差進行估計，運算量大；小波閾值去噪法具有實現簡單、計算量小、適用性廣泛等優點，目前對聲發射信號進行去噪大都采用此類方法。

本文對小波閾值去噪方法進行研究，將小波提純和小波閾值去噪相結合對聲發射信號進行處理。在小波提純的確定和閾值函數的選擇等方面進行分析，并分別從主觀和客觀兩個角度運用頻譜分析和信號能量百分比對去噪效果進行評判，結果證明本文所采用的方法去噪效果較好。

1 聲發射信號提純

本文采用的聲發射信號去噪主要包括對聲發射信號進行提純和對提純信號進行小波閾值去噪兩個部分。前者主要去除環境噪聲，后者主要將有用信號與背景噪聲最大限度的分離以提高信號去噪質量。聲發射信號的提純就是根據聲發射信號的特性，小波分解后只保留信號中有用頻帶的小波系數，其余小波系數（主要指噪聲）強制置零，對保留的有用頻帶信號進行小波重構。一般根據信號分解的高頻系數的差異性進行提純，本文將在此基礎上，通過各高頻系數所占的能量百分比及提純前后信號的頻譜分析對提純進行進一步確定和驗證，主要分為以下三步：

步驟1：從分解的高頻系數作初步主觀判斷；

步驟2：通過各高頻系數所占的能量百分比（見表1）來確定提純；

步驟3：通過頻譜分析進一步驗證。

首先采用Db5小波基函數對聲發射信號進行5層小波分解，分解結果如圖1所示。從圖1中可以看出小波分解高頻系數的第一、二、三層幾乎是噪聲，可以對其直接進行置零，用層的小波系數進行重構。

為了更進一步地對提純信號進行驗證，采集到的聲發射信號通過Matlab進行傅里葉變換，分別得出原始信號和提純信號的頻譜。從圖2中可以看出原始信號和提純信號的頻譜范圍大體一致，即可以認為小波分解的低頻層層小波系數幾乎包含了全部聲發射信號的有用部分。進一步驗證了可以直接用層系數進行小波重構，還原聲發射信號的有用部分。

2 小波閾值去噪原理

小波閾值去噪法是利用信號和噪聲的小波系數在不同尺度上分布和不同的幅值特性，通過設定閾值選擇大于閾值的信號對應的小波系數，去除小于閾值的噪聲對應的小波系數。小波閾值去噪過程中需要考慮的問題主要包括小波基函數、分解層數的確定，閾值門限及閾值函數的選取等。

2.1 小波基函數、分解層數及閾值門限的選取

常用的小波基函數主要包括Morlet，Haar，Meyer，Dubechies（N），Symlets（N）等，而小波基函數的選取往往從四個方面的特性入手進行考慮，即正交性、緊支性、對稱性和消失矩。在實際的聲發射信號處理中，采集的數據量較大，為了減少小波系數的冗余信息量，降低計算量，會選擇具有離散小波變換能力的小波基函數。選擇具有緊支性的小波基函數，可以提高對信號局部化分析的能力，同時也可以減少計算誤差。擁有某階次消失矩的小波基函數可以分辨聲發射信號與噪聲的特征。在小波分解與小波重構的過程中希望能夠最大限度地保留信號的真實度，而對稱的函數具有線性相位，就可以避免或減少信號的失真。結合以上分析和文獻[2?3]，本文將選取Db5作為小波基函數，確定分解層數為5層。

目前，常用的閾值門限主要有rigrsure，heursure，sqtwolog和minimaxi四種準則。由文獻[4]得出，從聲發射信號的去噪效果來看，無偏風險閾值（rigrsure）的效果是最好的。因此，本文將采用無偏風險閾值（rigrsure）作為選取閾值門限的閾值準則。

2.2 閾值函數的選擇

傳統的閾值函數包括硬閾值和軟閾值。設為小波變換系數，為估計的小波系數，為小波分解的尺度，為閾值。

從上述表達式可以看出，在硬閾值函數中，當小波系數的模大于閾值門限時，此時的小波系數為估計小波系數；而小波系數的模小于閾值門限時，將此時的小波系數置零，這表明硬閾值函數具有不連續性。在閾值處理的過程中獲得的估計小波系數是不連續的，重構信號時會出現吉布斯振蕩現象。軟閾值函數雖然連續性好，但當小波系數較大時，使得與存在固定偏差，這給信號重構帶來不可避免的誤差。

針對以上方法的不足，一些學者在此基礎上做了改進，如軟硬閾值折中法、加權平均法、開三次方處理法和指數閾值法等[5?7]，通過運用這些方法對構造的含噪信號進行去噪，并比較去噪信號的信噪比與均方根誤差，得出指數閾值法的去噪效果更好。其表達式為：

式中參數的取值范圍是。此方法中，隨著信號小波系數的增大，偏差會逐漸接近于選取合適的值就會得到比較好的去噪效果。

3 實驗驗證

實驗選用北京鵬翔科技公司的PXR15壓電式傳感器作為聲發射傳感器，運用敲擊鋼板的方法模擬聲發射信號，采用上述方法對實驗采集到的聲發射信號先提純，后進行指數閾值去噪，并對去噪效果從能量百分比和頻譜分析的角度進行評價。

圖3為采用上述方法對實驗中聲發射信號進行提純和閾值去噪后的波形。為了客觀分析去噪效果，采用能量百分比進行評價。分別對圖3中原始信號、提純信號和去噪信號的0～1 000點的數據，即噪聲段的去噪效果進行分析。分別求出其能量，并以原始信號的噪聲段為基準，求得能量百分比。如表2所示，提純信號在0～1 000點的噪聲能量所占百分比為14%，閾值去噪后信號的能量所占百分比為10%，因此去噪后的信號比提純后的信號濾除噪聲更徹底。

如圖4所示為原始信號、閾值去噪后的信號及濾除的噪聲。分別求得三者的能量，并以原始信號為基準求出對應的能量百分比，如表3所示。從圖4，表3中可以看出該方法去噪效果明顯，且去噪后的信號幾乎包含所有的聲發射信號，避免了信號失真。

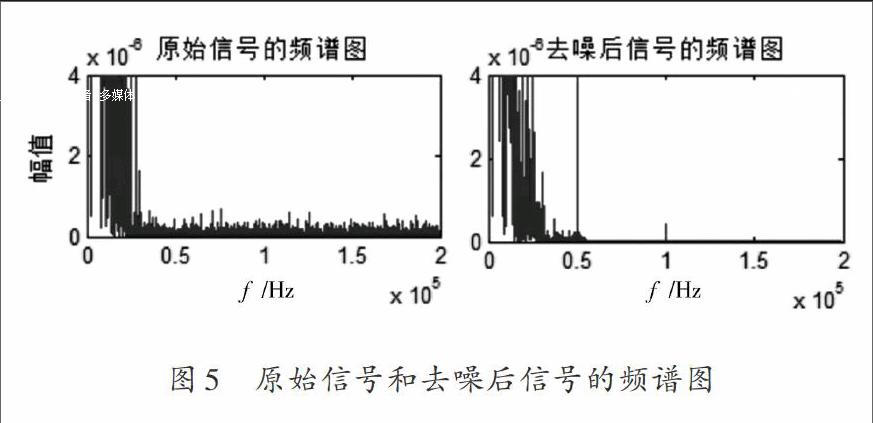
為了能夠進一步說明去噪效果，對實驗采集到的原始信號和去噪后的信號分別進行傅里葉變換得出二者的頻譜圖，如圖5所示。從圖5中可以進一步看出，通過采用文中的去噪方法，可以在避免失真的前提下有效濾除聲發射信號中的噪聲，去噪效果較好。

4 結 語

本文對小波提純的原理、方法以及小波閾值去噪相關參數的選取等進行了研究，并將二者結合對聲發射信號進行處理。分別從主觀和客觀兩個方面，運用頻譜分析和信號能量百分比對去噪效果進行評判。從實驗結果可以得出，采用本文方法可以有效濾除聲發射信號中的噪聲，且很好地保存了信號的完整度，避免信號失真，充分證明了該方法的可靠性和有效性。

參考文獻

[1] SATOUR A， MONTR?SOR S， BENTAHAR M， et al. Acoustic emission signal denoising to improve damage analysis in glass fibre?reinforced composites [J]. Nondestructive testing and evaluation， 2013， 29（1）： 65?79.

[2] 趙靜榮.聲發射信號處理系統與源識別方法的研究[D].長春：吉林大學，2010.

[3] 趙轉哲，姜忠宇，何慧娟.基于聲發射技術的鐵路貨車滾動軸承故障診斷研究[J].新技術新工藝，2009（5）：64?67.

[4] 劉洋，趙志洋，王冬蕾.基于LabVIEW的聲發射信號小波閾值去噪研究[J].氣象水文海洋儀器，2007（4）：16?19.

[5] 田曉春，陳家斌，韓勇強，等.一種優化的小波閾值去噪方法在行人導航系統中的應用[J].中國慣性技術學報，2015，23（4）：442?445.

[6] 張翔，王海彬，楊軍超.用于多普勒回波去噪的雙重指數型閾值函數[J].探測與控制學報，2014，36（5）：38?42.

[7] 王栓中， 朱玉田.改進小波閾值去噪法的對比性仿真實驗與分析[J].噪聲與振動控制，2012（1）：128?132.