集中荷載作用下扭轉支撐懸臂梁彎扭屈曲分析

劉迎春, 鄧世林, 張文福, 計 靜, 盧召紅, 李 洋

( 1. 東北石油大學 黑龍江省防災減災工程與防護工程重點實驗室,黑龍江 大慶 163318； 2. 東北石油大學 土木建筑工程學院,黑龍江 大慶 163318； 3. 南京工程學院 建筑工程學院, 江蘇 南京 211167 )

集中荷載作用下扭轉支撐懸臂梁彎扭屈曲分析

劉迎春1,2, 鄧世林1,2, 張文福1,3, 計 靜1,2, 盧召紅1,2, 李 洋1,2

( 1. 東北石油大學 黑龍江省防災減災工程與防護工程重點實驗室,黑龍江 大慶 163318； 2. 東北石油大學 土木建筑工程學院,黑龍江 大慶 163318； 3. 南京工程學院 建筑工程學院, 江蘇 南京 211167 )

采用能量變分法，建立集中荷載作用下扭轉支撐懸臂鋼梁彎扭屈曲的總勢能方程，選取6項三角級數表達的位移函數和轉角函數，引入無量綱參數，計算扭轉支撐懸臂鋼梁彎扭屈曲的無量綱臨界彎矩解析解；采用1stOpt數學優化分析軟件,擬合扭轉支撐懸臂鋼梁無量綱臨界彎矩計算公式；采用ANSYS有限元分析軟件進行驗證，研究荷載作用位置對懸臂鋼梁彎扭屈曲強度的影響。結果表明，扭轉支撐懸臂鋼梁無量綱臨界彎矩計算公式具有較高的精確性，為懸臂梁設計和穩定性研究提供參考。

彎扭屈曲； 懸臂鋼梁； 扭轉支撐； 集中荷載； 能量變分法； 有限元法

0 引言

懸臂鋼梁是工程常用的結構構件之一，人們關注其穩定性理論與試驗研究。Clark J W等[1]把簡支梁臨界彎矩公式用于懸臂梁計算，給出集中荷載和均布荷載作用下系數的取值范圍；對于矩形截面懸臂梁，Timoshenko S P等[2]利用Bessel函數,研究兩種作用于截面剪心的橫向荷載，給出臨界荷載計算公式；Woolcock S T等[3]給出矩形截面和雙軸對稱的工字型截面梁彎扭屈曲的數值解和試驗解；對于橫向荷載作用于截面上翼緣、剪心和下翼緣三種工況，Wang C M等[4]利用能量法研究單軸對稱懸臂梁的穩定性，提出屈曲荷載的計算公式；Trahair N S[5]利用有限元分析方法，考慮荷載作用于截面不同高度的影響，研究雙軸對稱懸臂梁，得到近似計算公式；Zhang L等[6]提出一種新的薄壁截面梁理論，利用能量法研究懸臂梁的整體穩定性，得到懸臂梁的近似計算公式；秦樺等[7]考慮集中荷載作用于上翼緣、下翼緣工況，分析單軸對稱工字型截面懸臂鋼梁的整體穩定性，得到懸臂梁彎扭屈曲的臨界荷載，提出懸臂梁的等效彎矩系數、彈性整體穩定系數和彈塑性整體穩定系數的計算公式。

這些研究未考慮懸臂梁自由端受約束情況，在實際工程中，懸臂鋼梁通常在端部與其他構件相連，如在常見的鋼結構雨篷或其他懸挑結構中，有縱向鋼梁或支撐構件與橫向懸臂鋼梁連接，為鋼梁提供側向約束或扭轉約束作用，能夠提高懸臂鋼梁的穩定性。Taylor A C等[8]用有限元方法研究受不同荷載作用的、跨中受約束作用的鋼梁的整體穩定性；Mutton B R等[9]研究跨中設置側向支撐和扭轉約束的簡支梁，用近似理論推導鋼梁的臨界荷載；Valentino J等[10]對跨中設置側向扭轉支撐的簡支鋼梁進行彈塑性彎扭屈曲分析，當跨中設置扭轉支撐時，可以提高鋼梁的屈曲強度；吳勇軍[11]研究不同荷載作用下工字型截面簡支鋼梁，當跨中設置一道支撐且考慮支撐位置沿截面高度變化時，得出支撐作用位置對整體穩定性的影響規律；趙滇生等[12]對兩端固定且受壓翼緣板有剛性側向支撐的H型截面鋼梁進行整體穩定承載力分析；岳潤慧等[13]用有限元方法，采用兩種側向支撐的設置方案對狗骨式鋼梁進行非線性屈曲分析，得到側向支撐間距對狗骨式鋼梁穩定承載力的影響規律；陳紹蕃[14-15]對無側向約束和有側向約束的工字型截面鋼梁進行承載力分析；Mohammadi E等[16]研究純彎作用下單軸對稱的簡支梁，提出彎扭屈曲公式和支撐剛度需求公式；Zhang W F等[17]利用能量變分原理，研究集中荷載和均布荷載作用下、具有側向彈性支撐懸臂梁的彎扭屈曲，并提出理論公式。

目前，對懸臂梁彎扭屈曲的研究較多，但是對懸臂鋼梁作用扭轉支撐研究的報道較少。筆者采用能量變分法，分析集中荷載作用下、具有扭轉支撐的懸臂鋼梁的彎扭屈曲，選取6項三角級數表達的位移函數和轉角函數，引入無量綱參數，得到集中荷載作用下懸臂鋼梁的無量綱臨界彎矩解析解；通過非線性數據擬合，提出集中荷載作用下扭轉支撐懸臂梁無量綱彎扭屈曲公式，并采用ANSYS有限元分析軟件進行驗證；同時研究荷載作用位置對懸臂鋼梁彎扭屈曲強度的影響。

1 能量變分法

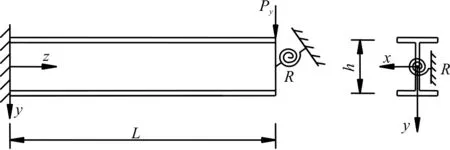
圖1 集中荷載下扭轉支撐懸臂梁計算模型

Fig.1 Calculation diagram of cantilever beam with torsional bracing under concentrated load

懸臂梁截面為雙軸對稱的工字型截面，其剪心S(0,0)和形心C(0,0)重合，扭轉支撐布置在懸臂梁懸臂端截面的剪心處，集中荷載作用下扭轉支撐懸臂梁計算模型見圖1，其中，L為懸臂鋼梁梁長；Py為懸臂端集中荷載；R為扭轉支撐剛度；h為上下兩個翼緣形心之間的距離。集中荷載作用下扭轉支撐懸臂梁的彎扭變形見圖2，其中,u為截面剪

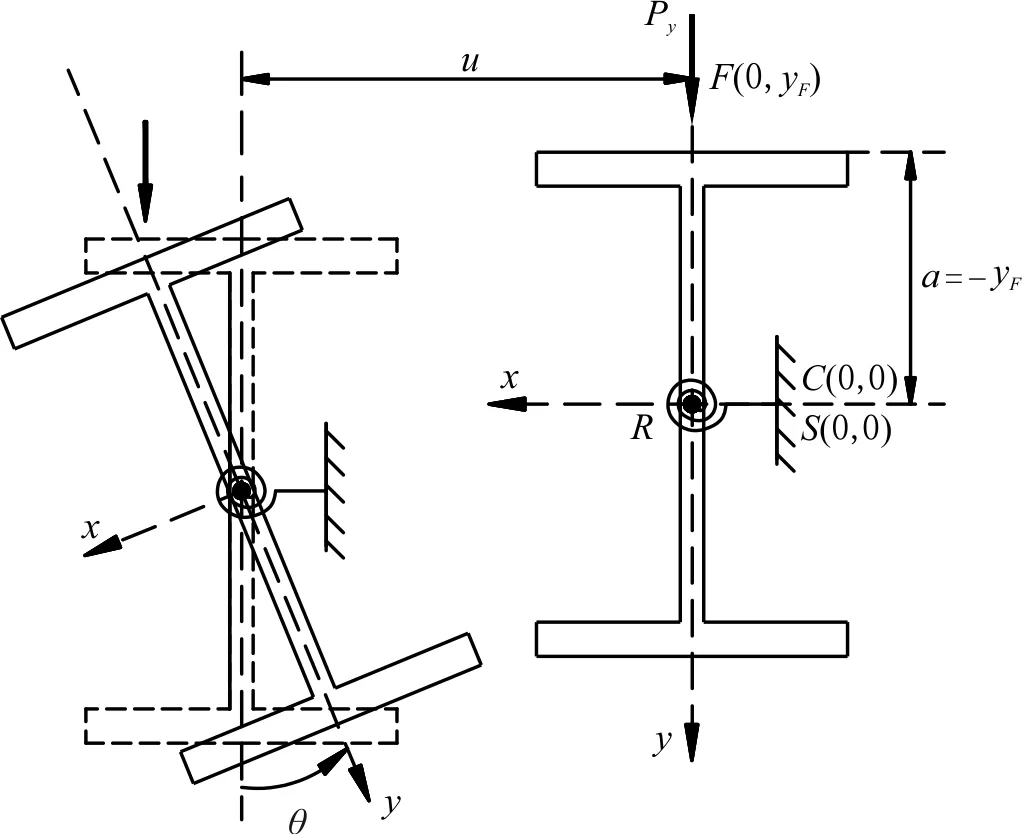
圖2 集中荷載作用下扭轉支撐懸臂梁的彎扭變形Fig.2 Flexural-torsional deformations of cantilever beam with torsional bracing

心的側向位移；θ為截面繞剪心的扭轉角；yF為以形心C(0,0)為坐標原點的荷載作用點的y坐標值；a為荷載作用位置參數，由截面剪心S(0,0)的y坐標值減去橫向荷載作用點的y坐標值得到。

1.1 基本假設

材料滿足胡克定律；鋼梁的側扭變形是微小的；發生側向彎曲和扭轉時，構件截面形狀不變；忽略平面內截面變形。

1.2 位移函數和轉角函數

選取6項三角級數的位移函數和轉角函數：

(1)

式中：Ai為平面外側向位移的不確定常量；Bi為扭轉角的不確定常量；z為懸臂梁在跨度方向所在截面到荷載作用點之間的距離，0≤z≤L。

6項三角級數位移函數和轉角函數應滿足懸臂梁的邊界條件：

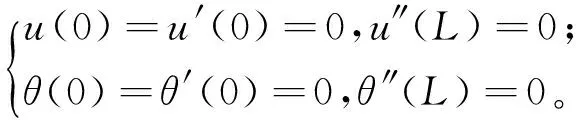
(2)

1.3 總勢能

無扭轉支撐作用的懸臂梁懸臂端受集中荷載作用的總勢能Πu表達式[18]為

(3)

扭轉支撐作用的懸臂梁扭轉支撐總勢能Ur表達式為

(4)

式(3-4)中：E為彈性模量；Iy為鋼梁繞y軸的慣性矩；u為截面剪心的側向位移；Iw為截面的翹曲慣性矩；θ為截面繞剪心的扭轉角；G為剪切模量；Jk為截面自由扭轉常數；Mx為繞截面強軸x的彎矩。

1.4 彎矩表達式

集中荷載作用下懸臂梁繞截面強軸x的彎矩Mx為

Mx(z)=-Py(L-z)。

(5)

1.5 無量綱屈曲方程

首先，將式(1)和式(5)代入式(3)，無扭轉支撐作用的懸臂梁懸臂端受集中荷載作用的總勢能表達式為

Πu=Π1+Π2+Π3+Π4+Π5,

(6)

其中

Π5=-Pyaθ2(L)=-(B1+B3+B5+B7+B9+B11)2Pya。

扭轉支撐作用的、懸臂梁懸臂端受集中荷載作用的總勢能Π表達式為

Π=Πu+Ur,

(7)

由最小勢能駐值原理[19-21]有

(8)

式(6-8)中：Π1、Π2、Π3為線性應變能；Π4為屈曲后彎矩分量Mxθ在側彎曲率作的功；Π5為屈曲時外力作的功。

然后，引進無量綱參數[22-23]有

(9)

將式(8)乘以L3/(EIyh2)，將式(9)代入式(8)并整理，寫成分塊矩陣的形式，得到無量綱彎扭屈曲方程：

(10)

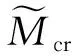
2 扭轉支撐懸臂鋼梁無量綱臨界彎矩計算公式

無扭轉支撐作用的懸臂梁臨界彎矩的計算公式[6]：

(11)

式中：a為荷載作用點到截面剪心(形心)的距離，當荷載作用點位于剪心上時為正；C1、C2為與荷載作用方式相關的因數，其計算公式為

(12a)

(12b)

對于受扭轉支撐作用的懸臂梁，采用1stOpt擬合軟件，對獲得的79 526組無量綱彎扭屈曲強度解析解進行非線性回歸，擬合集中荷載作用下扭轉支撐作用的懸臂梁無量綱臨界彎矩計算公式：

(13)

式中：a1,a2,a3,a4,a5為因數，取值見表1。

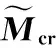
表1 式(13)量綱一臨界彎矩參數取值

3 模型驗證

3.1 有限元模型建立

采用ANSYS有限元軟件的SHELL63單元模擬工字型懸臂鋼梁。SHELL63作為薄壁單元，對彎曲變形采用經典的直線法假定，具有考慮板件彎曲變形和板面內薄膜變形的能力；每個單元有6個自由度，具有大變形和應力剛化的能力。采用COMBINE14彈簧單元模擬扭轉支撐，定義繞z軸的扭轉剛度R的取值，扭轉支撐設置在懸臂梁懸臂端剪心處。在單元劃分過程中，沿翼緣寬度方向分為8份，沿腹板高度方向分為8份，沿長度方向分為240份。建立的有限元模型見圖3。為滿足剛周邊假定，采用ANSYS有限元軟件的 CERIG 命令，沿梁跨度方向在各個截面建立繞z軸約束方程，以形成剛性區域。剛性區域沿梁長方向的分布見圖4。

3.2 邊界約束

為滿足理想的邊界條件,對于懸臂梁固定端支座，約束該截面上各節點所有自由度，即限制固定端截面在x、y和z方向的位移，以及繞x、y和z方向的轉角。自由端截面無任何約束。施加的懸臂梁邊界條件見圖5。

3.3 結果驗證

首先選取兩種國標H型鋼，分別為H500 mm×200 mm×10 mm×16 mm(L=8 m)和H600 mm×200 mm×11 mm×17 mm(L=10 m)，進行特征值屈曲分析[24]，計算臨界屈曲荷載，進而獲得臨界彎矩有限元解析解。然后進行集中荷載作用的屈曲彎矩理論值與有限元解析解對比，荷載作用點分別取上翼緣、剪心、下翼緣，結果見圖6和表2。懸臂梁作用扭轉支撐屈曲模態見圖7。

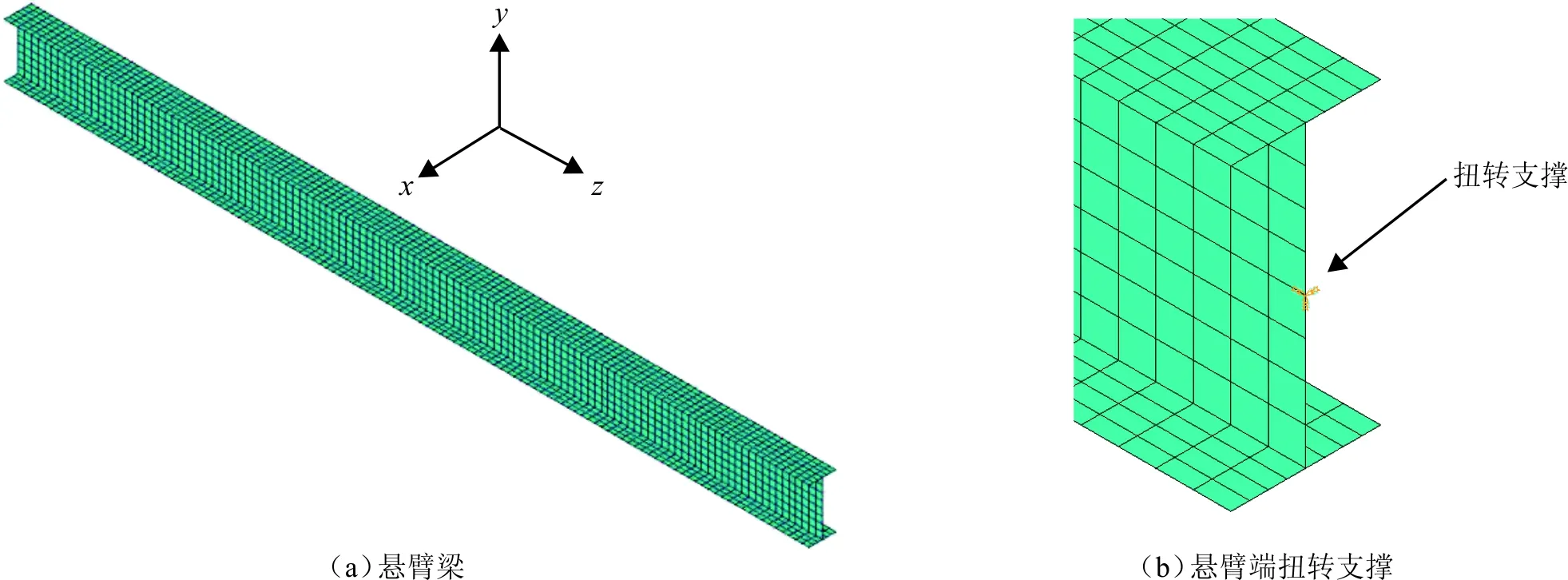
圖3 懸臂梁作用扭轉支撐有限元模型Fig.3 FEM model of cantilever steel beam with torsional bracing

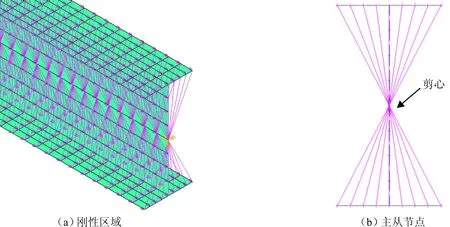
圖4 懸臂梁剛性區域沿梁長方向的分布Fig.4 Distribution of the rigid region along the length of beam

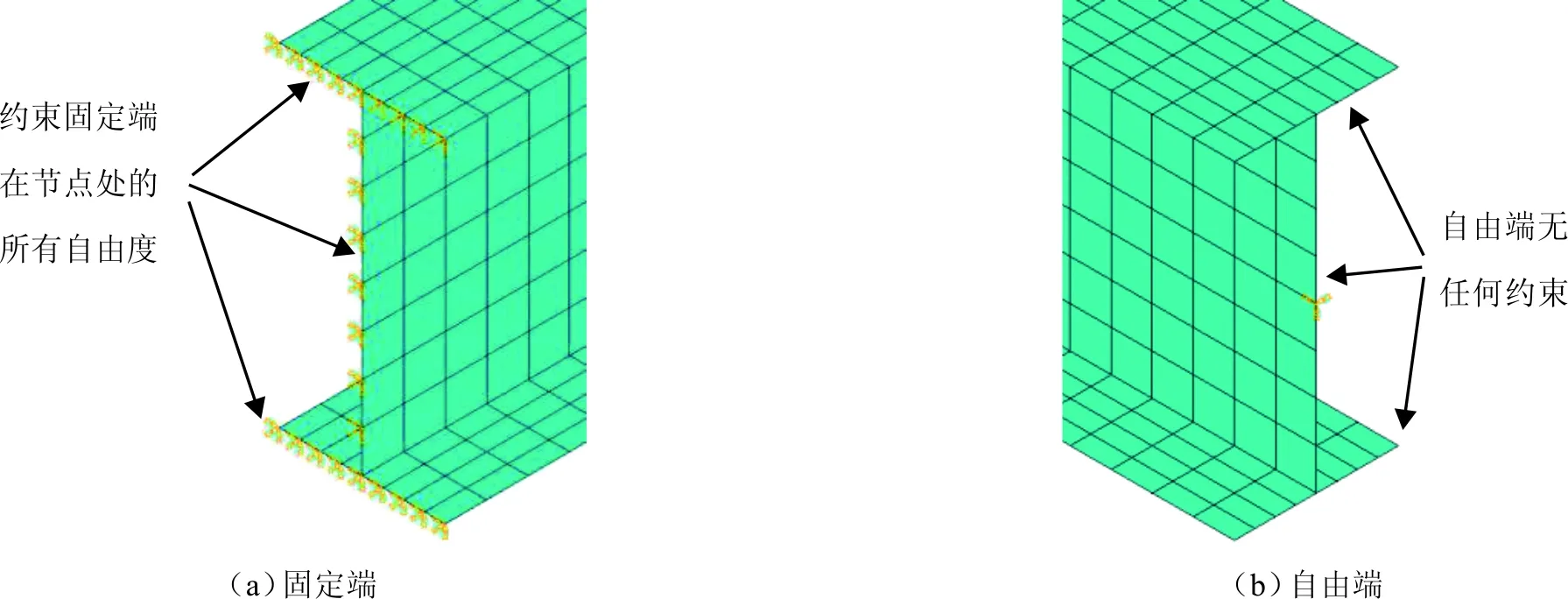
圖5 懸臂梁邊界條件Fig.5 Boundary conditions of cantilever beam

由圖6和表2可以看出，在一定范圍內，隨著扭轉支撐剛度的增加，懸臂梁的屈曲彎矩也隨之增加，施加扭轉支撐能夠提高懸臂梁的彎扭屈曲強度。同時，有限元計算結果與理論結果吻合良好，且計算的最大誤差在工程允許誤差(±5%)內，表明文中公式有較高的精確度。

3.4 荷載位置

選取兩種國標H型鋼，分別為H300 mm×200 mm×8 mm×12 mm(L=6 m)和H496 mm×199 mm×9 mm×14 mm(L=8 m)，研究荷載作用位置對懸臂梁彎扭屈曲強度的影響，結果見圖8。由圖8可以看出，荷載位置對懸臂梁彎扭屈曲強度的影響較大，荷載作用于下翼緣時，懸臂梁彎扭屈曲強度最大；作用于剪心時，次之；作用于上翼緣時，懸臂梁彎扭屈曲強度最小。

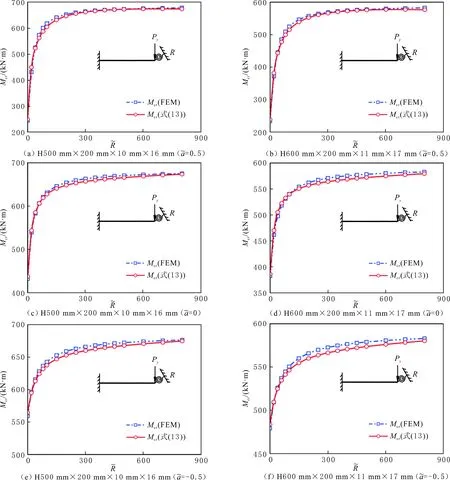
圖6 懸臂梁理論分析與有限元分析結果Fig.6 Comparison of theoretical analysis and finite element analysis

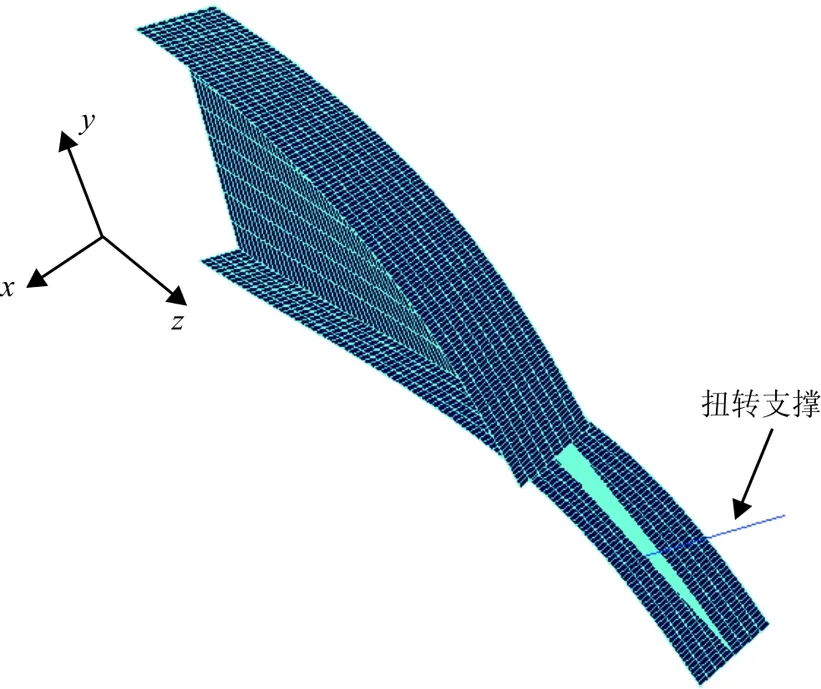
圖7 懸臂梁作用扭轉支撐屈曲模態

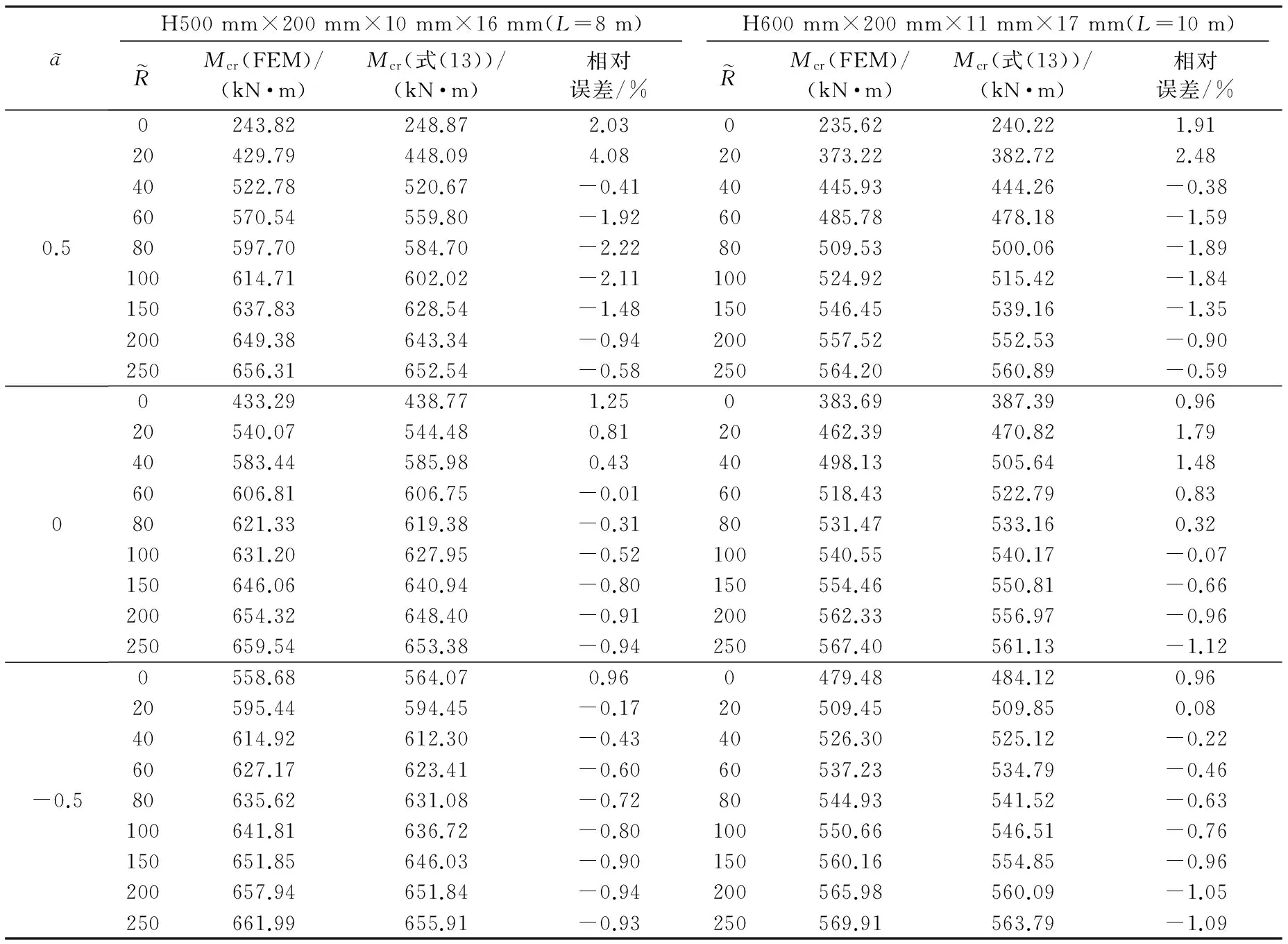
aH500mm×200mm×10mm×16mm(L=8m)H600mm×200mm×11mm×17mm(L=10m)RMcr(FEM)/(kN·m)Mcr(式(13))/(kN·m)相對誤差/%RMcr(FEM)/(kN·m)Mcr(式(13))/(kN·m)相對誤差/%0.50-0.50243.82248.872.030235.62240.221.9120429.79448.094.0820373.22382.722.4840522.78520.67-0.4140445.93444.26-0.3860570.54559.80-1.9260485.78478.18-1.5980597.70584.70-2.2280509.53500.06-1.89100614.71602.02-2.11100524.92515.42-1.84150637.83628.54-1.48150546.45539.16-1.35200649.38643.34-0.94200557.52552.53-0.90250656.31652.54-0.58250564.20560.89-0.590433.29438.771.250383.69387.390.9620540.07544.480.8120462.39470.821.7940583.44585.980.4340498.13505.641.4860606.81606.75-0.0160518.43522.790.8380621.33619.38-0.3180531.47533.160.32100631.20627.95-0.52100540.55540.17-0.07150646.06640.94-0.80150554.46550.81-0.66200654.32648.40-0.91200562.33556.97-0.96250659.54653.38-0.94250567.40561.13-1.120558.68564.070.960479.48484.120.9620595.44594.45-0.1720509.45509.850.0840614.92612.30-0.4340526.30525.12-0.2260627.17623.41-0.6060537.23534.79-0.4680635.62631.08-0.7280544.93541.52-0.63100641.81636.72-0.80100550.66546.51-0.76150651.85646.03-0.90150560.16554.85-0.96200657.94651.84-0.94200565.98560.09-1.05250661.99655.91-0.93250569.91563.79-1.09

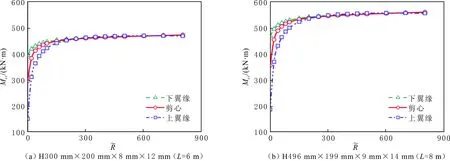
圖8 懸臂梁荷載作用位置的影響Fig.8 Effect of loading position of cantilever beam

4 結論

(1)根據扭轉支撐懸臂梁的能量方程，采用能量變分法，引入無量綱參數，對集中荷載作用下扭轉支撐懸臂梁進行彎扭屈曲分析，給出不同荷載作用位置的集中荷載作用下扭轉支撐懸臂梁無量綱彎扭屈曲的理論計算公式。經過有限元分析驗證，公式具有較高的精度，可為工程設計提供參考。

(2)隨著扭轉支撐剛度的增加，懸臂梁的彎扭屈曲強度也隨之增大。在工程實踐中，在懸臂梁端設置扭轉支撐(如與之側向連接的工字型鋼梁)對提高懸臂鋼梁的穩定性是有利的。

(3)對于具有扭轉支撐的懸臂鋼梁，荷載作用位置影響彎扭屈曲的臨界彎矩。當荷載作用于懸臂梁端的下翼緣時，臨界彎矩最大；作用于剪心時，次之；作用于上翼緣時，臨界彎矩最小。

[1] Clark J W, Hill H N. Lateral buckling of beams [J]. Journal of the Structural Division, ASCE, 1960,86(7):175-196.

[2] Timoshenko S P, Gere J M. Theory of elastic stability [M]. 2nd edition. New York: McGraw-Hill, 1961.

[3] Woolcock S T, Trahair N S. Post-buckling behavior of determinate beams [J]. Journal of Engineering Mechanics, 1974,100(2):151-171.

[4] Wang C M, Kitipornchai S. On stability of monosymmetric cantilevers [J]. Engineering Structures, 1986,8(3):169-180.

[5] Trahair N S. Flexural-torsional buckling of structures [M]. London: E & FN Spon, 1993.

[6] Zhang L, Tong G S. Elastic flexural-torsional buckling of thin-walled cantilevers [J]. Thin-Walled Structures, 2008,46:27-37.

[7] 秦樺,郭成喜.單軸對稱工字形截面懸臂鋼梁在橫向荷載作用下的整體穩定性研究[J].工程力學,2009,26(9):152-155. Qin Hua, Guo Chengxi. Stability of monosymmetric I-section cantilevers [J]. Engineering Mechanics, 2009,26(9):152-155.

[8] Taylor A C, Ojalvo M. Torsional restraint of lateral buckling [J]. American Society of Civil Engineers, 1966,92(2):115-129.

[9] Mutton B R, Trahair N S. Stiffness requirements for lateral bracing [J]. Journal of the Structural Division, ASCE, 1973,99(10):2167-2182.

[10] Valentino J, Pi Y L, Trahair N S. Inelastic buckling of steel beams with central torsional restraints [J]. Journal of Structural Engineering, 1997,123(9):1180-1186.

[11] 吳勇軍.支撐位置對鋼構件穩定承載力的影響[D].南京:河海大學,2005. Wu Yongjun. The effect to stability of steel members by bracing location [D]. Nanjing: Hehai University, 2005.

[12] 趙滇生,王樂洋,阮雪琴.上翼緣受側向支撐的固端鋼梁整體穩定分析[J].浙江工業大學學報,2007,35(6):687-690. Zhao Diansheng, Wang Leyang, Ruan Xueqin. Stability analyses of fixed end beam with lateral bracing on its top flange [J]. Journal of Zhejiang University of Technology, 2007,35(6):687-690.

[13] 岳潤慧,李軍,郁有升.狗骨式鋼梁側向支撐合理位置分析[J].鋼結構,2007,22(8):56-59. Yue Runhui, Li Jun, Yu Yousheng. Discussion on reasonable position of lateral brace for reduced beam section connection [J]. Steel Construction, 2007,22(8):56-59.

[14] 陳紹蕃.雙軸對稱工形截面無支撐簡支梁的整體穩定[J].鋼結構,2008,23(8):6-13. Chen Shaofan. Overall stability of unbraced simply-supported beams with doubly symmetric I-section [J]. Steel Construction, 2008,23(8):6-13.

[15] 陳紹蕃.有約束梁的整體穩定[J].鋼結構,2008,23(8):20-25. Chen Shaofan. Overall stability of beams with restraints [J]. Steel Construction, 2008,23(8):20-25.

[16] Mohammadi E, Hosseini S S, Rohanimanesh M S. Elastic lateral-torsional buckling strength and torsional bracing stiffness requirement for monosymmetric I-beams [J]. Thin-Walled Structures, 2016,104:116-125.

[17] Zhang W F, Liu Y C, Hou G L, et al. Lateral-torsional buckling analysis of cantilever beam with tip lateral elastic brace under uniform and concentrated load [J]. International Journal of Steel Structures, 2016,16(4):1161-1173.

[18] 童根樹.鋼結構平面外穩定[M].北京:中國建筑工業出版社,2006. Tong Genshu. Out-plane stability of steel structures [M]. Beijing: China Architecture & Building Press, 2006.

[19] 夏志斌,潘永昌.結構穩定理論[M].北京:中國建筑工業出版社,1988. Xia Zhibin, Pan Yongchang. Theory of structural stability [M]. Beijing: China Architecture & Building Press, 1988.

[20] 陳驥.鋼結構穩定理論與設計[M].北京:科學出版社,2012. Chen Ji. Stability of steel theory and design [M]. Beijing: Science Press, 2012.

[21] 張文福,杜娟,劉迎春,等.索桁架組合體系的固有振動能量變分解[J].東北石油大學學報,2013,37(5):103-108. Zhang Wenfu, Du Juan, Liu Yingchun, et al. Energy variational solution for the nature vibration of the cable-trusses combination system [J]. Journal of Northeast Petroleum University, 2013,37(5):103-108.

[22] 柳凱議.雙跨鋼梁的屈曲分析與應用[D].大慶:大慶石油學院,2009. Liu Kaiyi. Elastic lateral buckling and application of double span continuous beams [D]. Daqing: Daqing Petroleum Institute, 2009.

[23] 侯桂蘭.具有側向彈性支撐鋼梁的穩定性能研究[D].大慶:東北石油大學,2012. Hou Guilan. Stability research of steel beams with lateral elastic brace [D]. Daqing: Northeast Petroleum University, 2012.

[24] 計靜,徐智超,張文福,等.矩形鋼管混凝土翼緣的H型蜂窩組合柱特征值屈曲性能[J].東北石油大學學報,2017,41(1):106-116. Ji Jing, Xu Zhichao, Zhang Wenfu, et al. Eigenvalue buckling analysis of H-type honeycombed composite column with rectangular concrete-filled steel tube flanges [J]. Journal of Northeast Petroleum University, 2017,41(1):106-116.

2017-02-27；編輯：任志平

國家自然科學基金項目(51178087；51578120)；中國石油科技創新基金研究項目(2016D-5007-0608)；東北石油大學校青年科學基金項目(NEPUQN2014-25)；南京工程學院科研基金項目(YKJ201617)；國家自然科學基金東北石油大學校培育基金項目(NEPUPY-1-16)；東北石油大學校級研究生創新科研項目(YJSCX2016-031NEPU)；黑龍江省教育廳科研專項經費東北石油大學優勢科研方向凝練基金項目(2016YSFX-02)；黑龍江省大學生創新創業訓練重點項目(201610220015)

劉迎春(1980-)，女，博士研究生，副教授，主要從事土木結構工程方面的研究。

TU392.1;TU311.2;TU318.1

A

2095-4107(2017)03-0103-08

DOI 10.3969/j.issn.2095-4107.2017.03.011