發展核心素養的數學教學設計構想

李霞+徐鐸厚

摘 要：從核心素養形成的角度出發，設計并實施“多邊形及其內角和”一節的教學，需要讓學生在思辨中形成概念，在化歸中探尋策略，在類比中突破重點，在發散中豐富智慧，以此使學生學會用數學的眼光看世界，為終身發展而學習.

關鍵詞：多邊形內角和；教學設計；構想

“中國學生發展核心素養”所指向的“學生應具備的能夠適應終身發展和社會發展需要的必備品格和關鍵能力”的意蘊和旨趣，彰顯教師的教育智慧.數學核心素養要從教學行為與習慣的培養著手.

就拿“多邊形及其內角和”來說，不論是概念的得出，還是公式的形成，都蘊含眾多“關鍵能力”的形成要素.更進一步說，若教師舍棄“抓干的、來實的”的習慣做法，力透紙背，深入挖掘教材內容所承載的“關鍵能力”素材，將教學按照學生的認知邏輯展開，在“去粗取精、去偽存真、由表及里、由此及彼”的過程中，達成核心素養指向下的學生發展目標，課堂就會充溢智慧的霞光，絢麗而多姿.

一、在思辨中形成概念

本節課涉及眾多相關概念，但“萬物生長靠太陽”，再多的概念總有源頭，這里的源頭就是“多邊形”，其關鍵點就是“多”.眾所周知，“多”與“少”是相對的，此刻就需要教師指導學生認識“多”與“少”的辯證關系.多邊形是新學內容，多到什么程度暫且不論，但“少”要少到什么程度呢？這就牽扯概念中的另一個關鍵字“邊”.本節課是從“邊”的多少出發研究圖形，無邊不成形，因此，從理論上講，邊（亦即線段）的數量最少是1，可以是2，學生也學過邊數為3的三角形和邊數為4的四邊形.邊數為1和2時，是開放式圖形，屬于“線段（直線、射線）”和“角”，三角形、四邊形等才屬于“多邊形”意義下的“形”.從“少”出發，學生就會發現：多邊形中的“邊”，是線段；多邊形是封閉圖形；邊數最少的多邊形是三角形.

從“多”出發，學生就會發現，隨著邊數的增加，多邊形中的一些元素也會發生一些變化：頂點增加；內角的個數增加；內角和會發生怎樣的變化？有沒有規律可循？（此時，學生的經驗是三角形的內角和為180°，四邊形的內角和為360°）由內及外，那外角和會發生怎樣的變化？到此，又會牽扯出另一個問題：當多邊形的邊數無窮多時，多邊形會發生什么樣的變化？相關的要素又會發生怎樣的變化？顯然，這樣的思考又是形成和發展極限思想的良好素材.

這樣展開的教學，對學生發展來說因嵌入了學生的思考與發現，會比單純按照學科邏輯（逐一交代概念）展開更使學生興趣盎然.如果給予學生預習、討論等“自由”的時間足夠長，抑或是讓每一個學生都把自己獨立而獨特的思考展示出來，說不定還能在凸多邊形與凹多邊形的比較中有更多的發現，求異思維的能力也會順勢得以培養.

有了這樣的思考，學生理解教材中的多邊形的概念及其相關內容——“在平面內，由一些線段首尾順次相接組成的封閉圖形叫作多邊形.多邊形按組成它的線段的條數分為三角形、四邊形、五邊形、六邊形……由n條線段組成的多邊形就叫作n邊形”，就會更透徹.同樣，多邊形的角——內角、外角——連同內角和、外角和以及正多邊形、多邊形的對角線等，也不會存在理解的難度了.此處不再贅述.

二、在化歸中探尋策略

從上述分析可以看出，三角形是邊數最少的多邊形，隨著邊數的增多，相關要素都會發生變化.從變化的觀點出發，有兩種可能：有規律的變化和無規律的變化.這就會生發“多邊形的內角和與邊的數量”之間存有什么樣的關系的思考.對于這樣的問題，學生可能會有無從下手的思維癥結，就需要從思維的角度出發，找到突破的辦法.從思維角度來講，不論哪個學科，哪個領域，遇到復雜問題的時候，都會采用“復雜問題簡單化”這一策略.在科學實驗中經常運用的“控制變量法”，就是將復雜問題簡單化處置的典型.面對“多邊形”這一復雜問題，就要思考“最簡單的多邊形是什么圖形”.前已述及，三角形就是最簡單的多邊形.這就找到了破解多邊形相關問題的思維原點——三角形，這也是解決問題的出發點，由此引發學生去思考“如何將多邊形變為三角形”的問題.

三、在類比中突破重點

從三角形出發考慮多邊形問題，就要找到多邊形轉化為三角形的辦法.其實，學生在這之前已經接觸到解決這一問題辦法，那就是求四邊形內角和時所采用的“通過連接對角線將一個四邊形變為兩個三角形”，用這種類比的思想，不難發現，把四邊形的對角線一連，就會出現兩個三角形，那四邊形的內角和就是兩個三角形的內角和，即360°；對于五邊形，可以通過連接對角線的方式，變為三個三角形，其內角和就是540°；以此類推，個數有限的多邊形，其內角和的度數是可以計算出來的.從以上解決方式可以看出，“對角線”以及通過連接對角線而形成的“三角形”，就是解決多邊形內角和問題的關鍵，對角線則是撬動多邊形內角和問題的支點.

有了以上分析作鋪墊，再讓學生完成表1中的要求，學生自然興趣盎然.

當學生完成這個表格后，多邊形內角和的公式也就得到了：n邊形的內角和等于（n-2）×180°.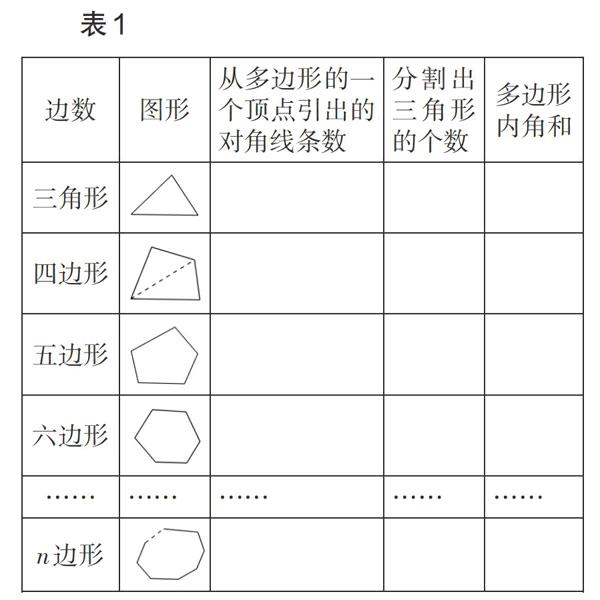

四、在發散中豐富智慧

一個問題的解決，不會只有一個辦法，否則，就不會有“條條大路通羅馬”之說.唯有從多個角度探尋解決同一個問題的辦法，學生的思維才能發散開來，并不斷促使學生窮盡思維，進而理順思維，優化思維，實現由解決一個問題向解決一類問題的突變，達到思維躍遷、智慧豐富之目的，生發不斷創新的力量.

前述方法是從對角線出發，找到了一個解決多邊形內角和的辦法，再探尋其他辦法，又應該如何思考呢？這還要回到幾何圖形的構成要素上尋找突破.

構成幾何圖形的基本要素，無非就是點、線、面.有的要素一目了然，比如，多邊形中的邊、頂點，有的要素則隱含在圖形中，需要思考才能找到，比如剛才用過的對角線，類似的還有一些圖形的高、角平分線、中線等等.上述解決問題的過程中，就是從多邊形的一個頂點出發，在不相鄰的另一個頂點間畫出對角線，從而化歸到三角形而找到了解決問題的支點.如此，同樣從“點”這一思考原點出發，只是改變“點”的原始位置，比如，選擇一條邊的任意一個點構造出三角形，或者在多邊形內（外）任意一個點構造三角形，都不失為可以采用的辦法.這樣，原來的“固定點”就會變為“移動點”“任意點”，而中考題中的重頭戲，也往往如此選擇.限于篇幅，簡述如下：

方法二：在n邊形的一邊上任取一點，把這一點與各頂點聯結，把n邊形分割為（n-1）個三角形，這些三角形的內角和比n邊形的內角和多出了一個平角，因此，n邊形的內角和=（n-1）×180°-180，即為：（n-2）×180°.

方法三：在n邊形內任取一點，然后把這一點與各頂點聯結，將n邊形分割為n個三角形，這n個三角形的內角和比n邊形的內角和恰好多了一個周角360°，因此n邊形的內角和=180°×n-360°，即為：（n-2）×180°.

方法四：在n邊形外任取一點，然后把這一點與各頂點聯結，將n邊形分割為n個三角形，這n個三角形的內角和比n邊形的內角和恰好多出了兩個三角形內角和，因此n邊形的內角和=n×180°-2×180°，即為：（n-2）×180°.

形成了這樣的思維習慣，學生在今后的學習、工作、生活中，也會主動尋求“由靜到動”“由此及彼”的途徑，豁然開朗的就不僅是學習過程，會更多地表現在人生的幸福中.

從以上分析可以看出，本節內容涉及眾多利于學生核心素養發展的要素，諸如對立統一、量變質變、有限與無限、個性與共性、一般與特殊、絕對與相對等，都極富哲學意味，若一一展開，必定是一幅幅美麗的風景.

從核心素養形成的角度來說，學生學習數學的一個重要目的是要學會數學的思考，用數學的眼光去看世界.這就需要教師在數學教學中應當從邏輯的、歷史的、關系的等方面去展開，以“提出目標，創設情境，設計環節，窮極思維，形成技能，造就智慧”為終極追求，奠定學生終身發展的良好基礎.

可見，充溢著思辨的學習，不僅有茍且，還有詩和遠方！