利用網絡平臺上好解題復習課
——以“解三角形”教學為例
文︳吳華華
利用網絡平臺上好解題復習課
——以“解三角形”教學為例
文︳吳華華

現在高三階段的二輪復習,老師們往往拿著課本按部就班講題的現象很多,這樣做效果一般。通過多次的考試檢測,我們發現學生在考試中問題百出:基礎不牢,審題不到位,能力題做不出,計算不過關,等等。這緣于復習課容量大、節奏快、反饋不及時。信息技術的滲透,給復習課帶來了幫助。如何利用好現代信息技術解決課堂設計與教學容量大、節奏快、反饋不及時的矛盾?筆者以一節“解三角形之小題突破”教學研討課為例,呈現自己對高三的二輪復習課的設計與教學心得。
一、通過平臺及時反饋,完善知識體系。
首先通過局域網平臺向學生發布兩道高考試題:

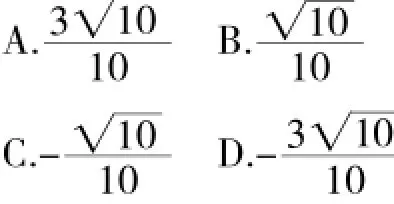
這兩道題涉及正余弦定理、三角恒等變換、向量等相關定理和方法,學生通過獨立完成,達到自我檢測的目的,同時梳理構建解三角形的知識體系和基本方法。
學生通過平臺將答案提交后,平臺上馬上就能顯示每道題的得分情況及學生的答題情況,為老師分析及講評提供了有效的依據。
由于第一題得分情況較好,我采用搶答方式,由學生自行搶答,簡要說明解題思路。對于第二題,由于有少部分學生出錯,我通過隨機點名的方式讓學生分享解題思路。
生A:過點A作AD彝BC,設AD=a,則BD=a,CD=利用余弦定理cos蟻BAC=
師:還有其他解法嗎?
生B:先用正弦定理求sin蟻BAC,再用平方和公式求cos蟻BAC。
生C:cos蟻BAC不知道正負。
生B:已知蟻BAD等于45°,且tan蟻DAC=2>1,所以蟻DAC>45°。則蟻BAC大于90°,所以結果為負值。
師:按這樣的思路,還有什么捷徑嗎?
學生在教師的引導下進一步思考,發現通過對蟻BAC范圍的約束,也能迅速找到正確答案。教師趁機強調選擇題做法的特殊性。
師:誰還有別的解法嗎?
生D:以D為原點,分別以BC,DA為x,y軸建立直角坐標系,利用向量法求解。
這里的一問一答,以及學生的互相補充,能幫助學生逐漸完善知識體系。教師引導學生注重方法的整理,學會自我歸納和總結。同時,網絡平臺的運用,課堂練習結果的及時反饋也能讓每個學生完全投入到課堂中,全身心參與,提高效率。
二、突破重難點,有序遞進,展開有載體的深度學習。
本環節的設計要求例題的選擇有典型性,能體現學習的通性、通法。在一般能力的基礎上,通過對例題中的相關問題進行多角度、多層次的探索、思考和演變,對所要講解問題做橫向比較和縱向延伸,學生能有效地掌握解題的基本思路。根據平時學生的練習情況,這里我設計了兩類問題。
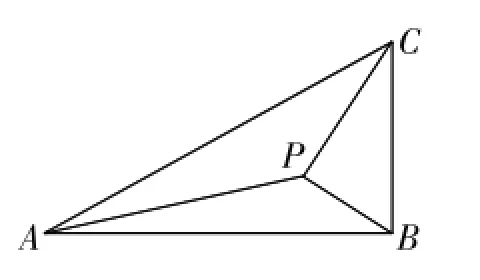
通過平臺,我得到了每個學生的完成情況。從提交情況來看,全班同學只有18人提交了完整的答題過程。這說明解答含多個三角形的問題對許多學生來說有一定的難度。為了讓學生們更好地掌握解題思路,我在提交了完整答題過程的學生中挑選了學生A,要他分析解題思路。
生A:設∠PBA=茲,則∠BCP=茲,所以BP=sin茲,又因為∠APB=150°,所以∠PAB=30°-茲。吟PAB中,化簡得
生B:根據題意易得∠CAP=茲,∠APC=120°, AC=2,CP=cos茲,吟APC中,化簡得
師:非常好!那么,這兩種方法的共同特征是什么?
教師引導學生把條件放到一個核心三角形內進行求解,得到解題關鍵。
網絡平臺的運用不僅能讓老師及時掌握學生的答題情況,更能讓學生充分展示自我。優生在展示優秀方法和答題過程獲得成就感的同時,也為其他同學提供了學習的榜樣,促進了學生良好書寫習慣的養成。同時,對于未能完成的學生,也可由學生們自行討論問題出現的原因,找到合適的方法,有序遞進地展開深度學習。
例2.已知a,b,c分別為吟ABC三個內角A, B,C的對邊,且
則(1)b+c的最大值是,
(2)b+2c的最大值是。
由于時間的關系,課堂上我只要求學生完成第一小問。從平臺所顯示的結果來看,大部分學生采用的是利用余弦定理和基本不等式求最值。此時我啟發學生:能不能用這種方法解決第二個問題?促使學生產生第二種解題思路:利用正弦定理建立關于∠B或∠C的三角函數關系式再求范圍。
反思
從教學實踐可以看到,網絡技術與教學過程的高度融合,使數字化技術的便利、快速的反饋、及時全面的展示與傳統教學模式的系統與深刻得到了優勢的整合,激發了學生學習的興趣和內在的潛能,促使每個學生積極投入到課堂,大大提高課堂學習的效率。學生的數學學習能力、數學思維品質、數學運算和數學建模等數學素養得到有效的提高。
(作者單位:長沙市長郡中學)

