位值制

文︳張新春

位值制

文︳張新春

討論位值制，我們應先區分位值制與進位制。事實上，相對于位值制而言，進位制出現得更早，更普遍。從某種意義上說，進位制是對刻痕記數的直接改進——刻痕記數，數是多少就刻多少道痕，對大數尤其是比較大的數而言，顯然不方便，于是很容易想到進位制。所謂進位制，就是以P個數組成一個新的單位，用一個新的符號表示。P個新的單位又組成一個更高的單位，用另一個符號表示。我們就把這個叫做P進制。P叫做進位的基。“如不算最原始的刻痕記數，古今中外的記數法都是進位制的”（梁宗巨，《世界數學通史》，遼寧教育出版社），而位值制則是在進位制的基礎上，對如何處理新的單位想到了漂亮的辦法。以下即詳述這種辦法。

我們不難發現，前面敘述的加法累數制的羅馬記數和乘法累數制的中國記數有一個共同特點：新的單位必須創造新的名稱——無論是羅馬的“X”和中國的“十”，都是表示新的單位的符號。而位值制的漂亮在于不需要創造新的符號表示新的單位。比如，表示“20”，不需要寫成“XX”或“二十”，只需要把表示“2”的符號寫到表示“十”的位置上即可。同樣是這個“2”，還可以表示“200”，或“2000”……一個數碼表示什么數值，就看它在什么位置上，這就是位值的含義。

中國算籌記數與位值制雛形

中國算籌記數法非常接近位值制。古代的算籌實際上是一根根同樣長短和粗細的小棍子，一般長為13~14cm，徑粗0.2~0.3cm，多用竹子制成。也有用木頭、獸骨、象牙、金屬等材料制成的。大約二百七十幾根為一束，放在一個布袋里，系在腰間隨身攜帶，需要記數和計算時就取出來。

在算籌記數法中，以縱橫兩種排列方式表示單位數目，其中1～5分別用縱橫方式排列相應數目的算籌表示，6～9則以上面的算籌加下面相應的算籌表示，此時上面的一根表示5（如下圖所示）。

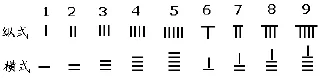
表示多位數時，個位用縱式，十位用橫式，百位用縱式，千位用橫式，依此類推，遇零則置空。據《孫子算經》記載，算籌記數法是“凡算之法，先識其位，一縱十橫，百立千僵，千十相望，萬百相當”。《夏陽侯算經》說“滿六以上，五在上方，六不積算，五不單張”。縱式和橫式的區別，再加上個位必用縱式的規定，較好地解決了空位的問題。比如，3740與374，如果沒有這樣的規定，用算籌擺出來就沒什么區別。再如，3704用算籌擺為：，由于7和4都是用的縱式，考慮到縱橫相間的規定，我們可以肯定7和4之間有一個0。而則表示374。

從這些例子可以看出，除了數碼的表現形式不同外，中國算籌記數已經和現在的十進位值制沒什么兩樣。特別是，后來為了明確起見，規定用○表示空位，就幾乎與現在的記數方法完全一樣了（值得說明的是，盡管有了縱橫相間和個位用縱式的規定，還是無法使算籌的擺法與所記的數形成一種一一對應的關系，比如，除了表示3704外，說它表示370004也無不可。當然，這兩者相差近百倍，根據所表示的數的實際意義或上下文進行理解也許不會產生混淆。但從理論上看，這是一個問題，于是，零這個符號“○”的發明成為必要）。

十進位值制

十進位值制記數法就是以10為基的位值制記數法。現在，我們用通用的阿拉伯數字0、1、2、3、4、5、6、7、8、9表示前幾個自然數。一個大的自然數，比如，四千五百七十八可以表示為：4000+500+70+8=4×103+5×102+7×10+8的形式，在十進位值制記數法中，這個數就用“4578”表示。

一般地，就整數而言，十進位值制通過“逢十進一”，把一個正整數從右到左分成個位、十位、百位、千位等，每個數位上的計數單位分別為一、十、百、千……，即依次為100，101，102，103……。十進位值制表示一個數的通用方式為：N=ak×10k+ak-1× 10k-1+…+a1×101+a0×100。其中a0，a1，a2，…，ak∈{0，1，2，3，4，5，6，7，8，9}且ak≠0。這種形式的N可簡記為akak-1ak-2·…·a1a0。若對每個ai都指定了具體的數，則上述記號中的橫線省略不寫。規定最高位不能為0是為了保證這種表示方式的唯一性。顯然，如果最高位可以是0，25就可以寫成025或0025，數的表示方式就不唯一了。在這種表示法之下，我們也稱N為k+1位數。很顯然，0不符合這種表示方式（因為0的最高位就是0），因此，我們通常不說0是幾位數。自然數中，最小的一位數是1。需要了解的是，“位數”這樣的概念概括的不是數的本質特征，而是與記數法有關的形式特征。以5為例，在十進位值制記數法之下，它是一位數；若在二進制記數法之下，它就記為1012，成為三位數了。

如前面所述，當前通用的數字為阿拉伯數字，但使用何種數字卻并非十進位值制的實質。比如，我們可以用零、一、二、……九表示，4785就表示為“四七八五”。事實上，阿拉伯數字剛傳到歐洲，即引起當時的大數學家斐波拉契的高度關注。他在其名著《算盤書》中寫道：“這里的印度9個數字9，8，7，6，5，4，3，2，1，還有一個阿拉伯人稱之為零的符號0，可以把任何數表示出來，實在是一種理想的計數符號。”正是基于這種認識，他號召歐洲人用這種數字取代羅馬數字。隨后又經過諸多曲折，阿拉伯數字終于在16世紀得到廣泛的應用。

位值制記數法最重要的優點之一就是便于計算。“其計算規則可以用這些數字的加法表和乘法表的形式來表示，而且一旦記住，便可永遠運用自如。古代的計算技巧一度只限于少數專家所掌握，而現在則是小學里的課程了。像這樣的科學進步對日常生活有如此深刻影響，并帶來極大方便的例子還不是很多”（[美]R·柯朗，H·羅賓，《什么是數學》，復旦大學出版社，2008）。

在加法交換律和結合律的支持下：

而這一切又可寫成一種更簡單的形式（如右所示）。

于是，在十進位值制記數法之下，在運算定律的支持下，任意兩個數相加，通過以上豎式的計算程序（法則），可以轉化成一系列20以內加法的組合。而20以內的加法原則上都是需要記憶的。因此，在20以內加法的教學過程中，不管我們如何確定教學目標，“接受”“記憶”是必須的方法。一定的計算速度是必要的目標，不能簡單地將“接受”和“記憶”等同于“落后”。

對于乘法，也完全類似。有了十進位值制記數法，在乘法交換律、結合律以及分配律的支持下，任意兩數相乘都可以通過一定的程序（法則）轉化為一系列表內乘法和加法的組合。這里的程序（法則）可以用我們熟悉的乘法豎式表示，而表內乘法正如20以內的加法一樣，都是需要記憶的。于是，乘法口訣的教學也一樣，其最根本的目標是口訣能脫口而出。

數學教育的真功夫是對數學與數學教育的把握，唯此才能成就好的數學課堂。湖南數學教師的老朋友，《湖南教育》的申建春老師開通了微信公眾號“與數學老師談心”，請關注。