非線性耦合Drinfeld-Sokolov-Satsuma-Hirota方程的對稱約化

牛莉莉, 胡恒春

(上海理工大學 理學院,上海 200093)

非線性耦合Drinfeld-Sokolov-Satsuma-Hirota方程的對稱約化

牛莉莉, 胡恒春

(上海理工大學 理學院,上海 200093)

由Clarkson和Kruskal提出的Clarkson-Kruskal直接法是一種不涉及群運算的求解非線性偏微分方程的代數方法,不同于經典李群方法,Clarkson-Kruskal直接法不需要求解復雜的初值問題.應用Clarkson-Kruskal直接法,并且利用相應規則得到非線性耦合Drinfeld-Sokolov-Satsuma-Hirota方程的對稱約化.同時進一步求得了Drinfeld-Sokolov-Satsuma-Hirota方程新的相似變量和相似解,并與經典李群方法得到的結果進行對比,驗證了Clarkson-Kruskal直接法與經典李群方法得到的結果可以互相變換.

對稱約化; 非線性耦合Drinfeld-Sokolov-Satsuma-Hirota方程; Clarkson-Kruskal直接法

近年來,人們在不同科學領域中都發現和提出了用非線性方程來模擬不同的實驗模型.因此,找到非線性發展方程的解具有非常重要的研究意義.如何求解非線性發展方程是一項困難的工作,經過數學家們和物理學家們多年的不懈努力,人們提出了許多有效的求解非線性發展方程的方法,如:Weierstrass橢圓函數展開法[1]、達布變換法[2]、Hirota雙線性方法[3]、反散射方法[4]、李群方法[5-11]等.

本文研究Drinfeld-Sokolov-Satsuma-Hirota方程,簡稱DSSH方程,其形式如下:

(1)

該方程分別獨立地由Drinfeld,Sokolov[12]和Satsuma,Hirota[13]提出.耦合DSSH方程是眾多具有特殊形式Lax對的非線性方程之一,并且DSSH方程可以作為KP族的四約化的一個特殊情況,科學家們已經構建出它的精確單孤子解.Gürses和Karasu[14]發現了方程(1)的一個遞歸算子和一個雙哈密頓結構,Wazwaz[15]用3種不同的方法,也就是Cole-Hopf變換、Hirota雙線性方法和指數函數法,獲得了其多孤子解、多個單孤子解以及平面周期解.下面采用Clarkson-Kruskal直接法(簡稱CK直接法)對方程(1)進行約化,并求出選取特殊常數后的新的相似解.

1 方法簡介

眾所周知,求解非線性系統的約化相似解,有3種常用方法:經典李群法、非經典李群法以及CK直接法.其中,經典及非經典李群法用到李群的思想,并且只能得到非線性偏微分方程的部分相似約化.

1989年,Clarkson和Kruskal提出將CK直接法應用于Boussinesq方程[16]和修正的Boussinesq方程[17],并得到了新的相似解,而用經典李群法和非經典李群法是得不到這些結果的.這種方法的主要優點是避免了復雜的群論分析,并且有時能夠得到更多的相似約化結果.CK直接法被廣泛應用在求解各種非線性偏微分方程上,如:對稱正則長波方程[18]、修正的Benjamin-Bona-Mahoney 方程[18]等.

首先介紹相似變換的定義。

設u(x,t)是一個偏微分方程P(u)=0的解,作變換

(2)

使u′(x′,t′)也是偏微分方程P(u)=0的解,即

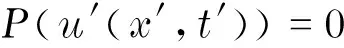
當式(2)為單參數李群變換時,可以得到從x,t,u(x,t)到x′,t′,u′(x′,t′)的不變變換條件

(3)

將式(2)代入到式(3)中可以確定ξ(x,t),τ(x,t),η(x,t),從而由式(3)的特征方程

確定出相似變量和相似變換.

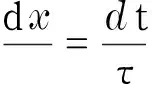
解得U(x,t,h(z,t),u)=c2,這時相似解可表示為

(4)

基于以上,可直接尋求形如式(4)的解.將式(4)代入到P(u)=0中,可得到ω(z)滿足的一個常微分方程,這是偏微分方程的一個一般的相似約化[19].

CK直接法[16-22]的基本思想是:對一個偏微分方程

(5)

尋找一個如下形式的相似解

這是相似約化最一般的形式.將式(4)代入式(5)中,并且確保得到的結果是關于ω(z)的常微分方程,并且限制U和它的導數條件,使之能夠解出U和ω的具體形式.

實際上,可以進一步假設方程(5)有如下形式的解

(6)

這里α(x,t),β(x,t),z(x,t)是關于x,t的待定函數.

將式(6)代入到方程(5)中,并且按ω(z)的冪次及其導數的階數進行整理.為了使得到的結果是關于ω(z)的常微分方程,需要求ω(z)(或其導數)的不同冪次項的系數成比例,并且比值只能是z的函數.因此可得到關于α(x,t),β(x,t),z(x,t)的超定方程組,便可解得方程(5)的相似約化.

2 Drinfeld-Sokolov-Satsuma-Hirota方程的相似約化

對于DSSH方程,應用CK法求其對稱約化、相似變量及相似解的步驟具體如下.

a. 可以容易證明,對于大部分方程都存在形式為u(x,t)=α(x,t)+β(x,t)ω(z(x,t))的相似約化,因此可假設方程(1)具有如下形式的對稱變換

(7)

式中:α1,α2,β1,β2以及z(x,t)是關于x,t的待定函數;P(z),Q(z)是關于z的常微分方程.

b. 將式(7)代入式(1)中,將得到的結果按照P(z),Q(z)的冪次及其導數的階數進行整理歸納得到

c. 找出其規范系數(假設為φ(x,t)),將P(z),Q(z)及其各階導數的系數寫成φ(x,t)Гi(z)的形式,其中Гi是z的待定函數.

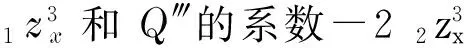
(10)

式中,Гi是關于z的待定函數.為計算方便,將經過一些運算后的Гi(z)仍記為Гi(z).

(11)

式中,Ωi是關于z的待定函數.

在接下來確定α1,α2,β1,β2和z時,在不失一般性,并且確保方法有效的前提下,對于DSSH方程,有以下5個自由度規則:

規則1 若α1(x,t)具有形式α1=α10(x,t)+β1(x,t)Ω(z(x,t)),那么取Ω(z)≡0(相當于作變換ω(z)→ω(z)-Ω(z));

規則2 若α2(x,t)具有形式α2=α20(x,t)+β2(x,t)Ω(z(x,t)),那么取Ω(z)≡0(相當于作變換ω(z)→ω(z)-Ω(z));

規則3 若β1(x,t)具有形式β1=β0(x,t).Ω(z(x,t)),那么取Ω(z)≡1(相當于作變換ω(z)→ω(z)/Ω(z));

規則4 若β2(x,t)具有形式β2=β0(x,t).Ω(z(x,t)),那么取Ω(z)≡1(相當于作變換ω(z)→ω(z)/Ω(z));

規則5 若z(x,t)是由方程Ω(z)=z0(x,t)確定的,那么取Ω(z)=z(相當于作變換z→Ω-1(z)).

接下來考慮zx的不同取值情況.

a. 當zx=0時,根據上述規則5可得,z是只關于t的函數,即z=t,因此P(z),Q(z)也是只關于t的函數,得到形式為一階常微分方程的約化方程.因此重點考慮zx≠0的情況.

b. 根據上述5個規則,當zx≠0時,在方程(10)中由P?和PP′前面的系數可知

(12)

進一步可得到

因此,利用規則3可知

(13)

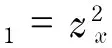
由規則5可知

再由規則5可得到z有如下形式

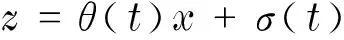
(14)

顯然,再由式(13)可得

(15)

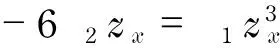
(16)

由上述規則2,便可得到

(17)

以及

(18)

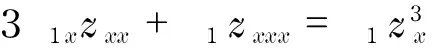
(19)

又因為z=θ(t)x+σ(t),方程(19)左邊是關于x的線性函數,因此Г2有如下形式:

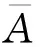
比較上述方程兩邊x的系數,可得

(20)

(21)

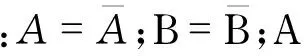
他們把這個消息報告李站長的時候，李站長雖然面上對放跑木材有些許惱怒，但當他看見卡車上粗壯奇秀的我時，頓時眉開眼笑，深諳當下苗木生意行情的他，心想這次搞到了一塊肥肉，沒收了就是公家的財物，實質上就是站里的財物，經過執法部門的拍賣就是合法的買賣，誰也說不起，看來上半年的創收任務有著落了。

因此,得到了非線性耦合DSSH方程的對稱約化為

(22)

將上述方程(20)～(22)代入方程(1)中,可得

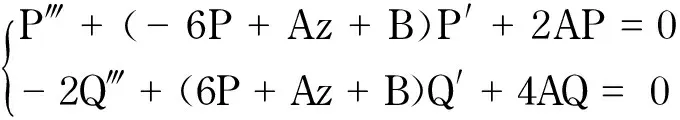
(23)

接下來考慮方程(23)的不同常數選取.

a. 當A=0時,可得到

式中,c1,c2是任意常數.

DSSH方程的對稱約化為

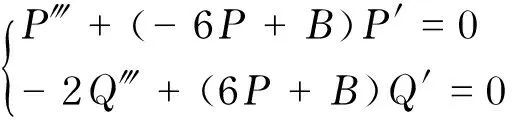
(24)

其中,P?+(-6P+B)P′=0的解為橢圓積分,其形式為

(25)

式中,c1,c2是常數.

b. 當A≠0時,解方程(20)和(21),分別可得到

式中,c1,c2是常數.

DSSH方程的對稱約化為

式中,P(z),Q(z)由方程(24)決定.

對以上CK直接法得到的相似約化作出適當的變換,便能夠得到由經典李群變換導出的相似約化.在經典李群變換中,若Drinfeld-Sokolov-Satsuma-Hirota方程通過如下變換具有不變性,

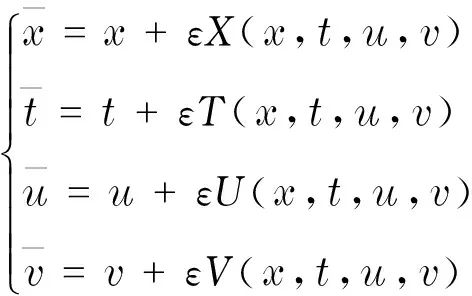
則群不變量z,P(z)以及Q(z)能夠通過求解以下特征方程

得到.

在經典李對稱中,群變換等價于

這里{σu,σv}是Drinfeld-Sokolov-Satsuma-Hirota方程對稱方程的解

(26)

下面對應用CK直接法求得的式(22)進行群論的解釋[23-24].

實際上,由已求得的式(14)可得到

即

同樣的方法,由u=θ3P(z),v=θ4Q(z)可得到

即

因此,方程的對稱約化具有如下形式:

(27)

若假設

即當A≠0時T=θ3,當A=0時T=1,式(27)求得的σ也是式(26)的解,也即由CK直接法求得的相似約化也可由經典李對稱方法求得.

3 結論與展望

首先介紹了CK直接法求解偏微分方程的基本思想及具體步驟,并應用于Drinfeld-Sokolov-Satsuma-Hirota方程,得到了方程的對稱約化以及其相似解.另外,比較了CK直接法和經典李群法的約化結果,可知CK直接法的結果可以推導出經典李群法的結果,即兩種方法求得的結果可以互相變換.如何尋找其他類型的偏微分方程的約化結果也是今后的研究重點之一.

[1] CHEN Y,YAN Z Y.The Weierstrass elliptic function expansion method and its applications in nonlinear wave equations[J].Chaos,Solitons & Fractals,2006,29(4):948-964.

[2] MATVEEV V B,SALLE M A.Darboux transformations and solitons[M].Berlin:Springer,1991.

[3] HIROTA R.The direct method in soliton theory[M].Cambridge:Cambridge University Press,2004.

[4] ABLOWITZ M J,CLARKSON P A.Solitons,nonlinear evolution equations and inverse scattering[M].Cambridge:Cambridge University Press,1992.

[5] BLUMAN G W,KUMEI S.Symmetries and differential equations: applied mathematical sciences[M].New York:Springer,1989.

[6] OLVER P J.Applications of Lie groups to differential equations:graduate texts in mathematics[M].New York:Springer,1993.

[7] OVSIANNIKOV L V.Group analysis of differential equations[M].New York:Academic Press,1982.

[8] IBRAGIMOV N H.CRC handbook of Lie group analysis of differential equations,volume I[M].Boca Raton:CRC Press,1993.

[9] IBRAGIMOV N H.CRC handbook of Lie group analysis of differential equations, volume II[M].Boca Raton:CRC Press,1994.

[10] IBRAGIMOV N H.CRC handbook of Lie group analysis of differential equations, volume III[M].Boca Raton:CRC Press,1995.

[11] ADEM K R,KHALIQUE C M.Exact solutions and conservation laws of a (2+1)-dimensional nonlinear KP-BBM equation[J].Abstract and Applied Analysis,2013,2013:791863.

[12] DRINFELD V G,SOKOLOV V V.Equations of Korteweg-de Vries type and simple Lie algebras[J].DokladyAkademiiNauk SSSR, 1981,258:11-16.

[13] SATSUMA J,HIROTA R.A coupled KdV equation is one case of the four-reduction of the KP hierarchy[J].Journal of the Physical Society of Japan,1982,51(10):3390-3397.

[14] GüRSES M,KARASU A.Integrable KdV systems: recursion operators of degree four[J].Physics Letters A,1999,251(4):247-249.

[15] WAZWAZ A M.The Cole-Hopf transformation and multiple soliton solutions for the integrable sixth-order Drinfeld-Sokolov-Satsuma-Hirota equation[J].Applied Mathematics and Computation,2009,207(1):248-255.

[16] CLARKSON P A,KRUSKAL M D.New similarity reductions of the Boussinesq equation[J].Journal of Mathematical Physics,1989,30(10):2201-2213.

[17] CLARKSON P A.New similarity solutions for the modified Boussinesq equation[J].Journal of Physics A:Mathematical and General,1989,22(13):2355-2367.

[18] CLARKSON P A.New similarity reductions and Painlevé analysis for the symmetric regularised long wave and modified Benjamin-Bona-Mahoney equations[J].Journal of Physics A:Mathematical and General,1989,22(18):3821-3848.

[19] CLARKSON P A,LUDLOW D K.Symmetry reductions,exact solutions,and Painlevé analysis for a generalized Boussinesq equation[J].Journal of Mathematical Analysis and Applications,1994,186(1):132-155.

[20] CLARKSON P A.Nonclassical symmetry reductions of the Boussinesq equation[J].Chaos,Solitons & Fractals,1995,5(12):2261-2301.

[21] CLARKSON P A,MANSFIELD E L,PRIESTLEY T J.Symmetries of a class of nonlinear third-order partial differential equations[J].Mathematical and Computer Modelling,1997,25(8/9):195-212.

[22] BLUMAN G W,COLE J D.Similarity methods for differential equations: applied mathematical sciences[M].New York:Springer,1974.

[23] MAN J.Similarity reductions and Painlevé property of coupled KdV equations[J].Communications in Theoretical Physics,2008,49(2):275-280.

[24] ADEM K R,KHALIQUEC M.On the solutions and conservation laws of the coupled Drinfeld-Sokolov-Satsuma-Hirotasystem[J].Boundary Value Problems,2014,2014:248.

(編輯:董 偉)

Symmetry Reduction for the Nonlinear Coupled Drinfeld-Sokolov-Satsuma-Hirota Equation

NIU Lili, HU Hengchun

(CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

The Clarkson-Kruskal direct method was proposed by Clarkson and Kruskal,which is an algebraic method for solving nonlinear partial differential equations.The advantage of this method is that it does not involve group theory operations and complex initial value problems.It can give new similarity solutions of the nonlinear evolution equations which could not be obtained by the classical Lie group method and the nonclassical Lie group method.By using the Clarkson-Kruskal method and corresponding rules,the symmetry reduction and the similarity transformation of the Drinfeld-Sokolov-Satsuma-Hirota equation were obtained.It is verified that the results by the Clarkson-Kruskal method can be transformed into those by the classical Lie group method.

symmetryreduction;nonlinearcoupledDrinfeld-Sokolov-Satsuma-Hirotaequation;Clarkson-Kruskaldirectmethod

1007-6735(2017)03-0205-05

10.13255/j.cnki.jusst.2017.03.001

2016-12-19

國家自然科學基金資助項目(11071164,11201302);上海市自然科學基金資助項目(10ZR1420800);上海市重點學科建設資助項目(XTKX2012)

牛莉莉(1993-),女,碩士研究生.研究方向:孤立子理論與可積系統.E-mail:546174910@qq.com

胡恒春(1976-),女,副教授.研究方向:孤立子理論與可積系統.E-mail:hhengchun@163.com

O 175

A