基于聲學層析成像的爐內溫度場重建算法研究

劉 廈， 劉 石

(華北電力大學 控制與計算機工程學院，北京 102206)

?

基于聲學層析成像的爐內溫度場重建算法研究

劉 廈， 劉 石

(華北電力大學 控制與計算機工程學院，北京 102206)

為了獲取快速準確的鍋爐溫度場在線監測信息，提出了一種基于聲學層析成像(AT)測量的代數重建-神經網絡(ART-NN)溫度場重建算法，該算法結合了代數重建方法(ART)和BP神經網絡方法的優勢.采用該算法對多種典型的溫度場模型進行數值仿真，分析了算法的重建結果和穩健性，并利用實驗研究進一步評估該算法的性能.結果表明：ART-NN算法的重建質量和穩健性要優于Tikhonov正則法、Landweber迭代法和ART方法，為提高鍋爐爐膛溫度場重建質量提供了一種有效方法.

聲學層析成像； 溫度場測量； 重建算法； ART方法； BP神經網絡

對大型電站鍋爐爐膛溫度場進行在線監測[1]具有重要意義，但受電站鍋爐尺寸大、爐內溫度高和工作環境惡劣等因素的限制，傳統測溫方法難以獲得準確的爐內溫度場.因此，迫切需要尋求一種快速、廉價、運行穩定且靈敏性高的測量方法用于鍋爐爐膛測溫.聲學層析成像(AT)測量以其非侵入、價格低廉等優點，被認為是一種具有發展前景的可視化測量方法.該技術還可應用于大氣邊界層[2]、海洋熱液口[3]及儲糧[4]等溫度場的監測.

AT測量方法的成功應用在一定程度上取決于重建算法的精度與速度[5].常見的重建算法主要有截斷奇異值分解法(TSVD)[6]、Landweber迭代法[7-8]、Tikhonov正則法[1,9]、代數重建算法(ART)[10-11]和聯合代數重建算法(SART)[12]等.TSVD方法通過截斷系數矩陣中近似于零的奇異值來確保穩定的數值解，但應用TSVD方法的一個主要問題在于多大的奇異值應該被截斷，特別是當矩陣的奇異值是連續下降的.從數值最優化方面來說，Landweber迭代法在本質上屬于最速下降法，存在收斂速度相對較慢、數值解過度光滑以及未能利用被重建對象的先驗信息等問題.Tikhonov正則法是一種有效的求解反問題方法，然而直接將該方法應用于溫度場重建時，效果并不理想.ART方法的優勢在于計算復雜性相對較低，但其存在易受噪聲干擾、收斂速度較慢等缺點.為解決這一不足，研究者們提出了SART方法，其原理是在ART基礎上對噪聲干擾進行了平滑處理.雖然該方法可降低噪聲干擾，提高收斂速度，但容易陷于局部極小點，導致重建質量降低.因此，在聲學法測量中如何獲取高質量的重建結果仍然是一個開放性的問題.關于反問題求解理論的介紹可進一步參考文獻[13]～文獻[15].

針對AT測量方法的特點，筆者提出了一種新的溫度場重建算法來改善重建質量.采用集成了ART方法和BP神經網絡方法優勢的重建算法來改善溫度場重建質量，利用數值仿真和實驗方法對溫度場進行重建，并對重建過程中的誤差和算法的穩健性進行分析.

1 聲學溫度場重建原理

AT測量方法是基于氣體介質中聲波傳播速度和該氣體介質溫度之間的函數關系[5]：

(1)

式中：γ為氣體比定壓熱容和比定容熱容之比；R為氣體常數；M為氣體摩爾質量；Z為氣體組成所決定的常數；T為氣體介質溫度；c為聲波傳播速度.

測量中，已知2個聲波收發器間的距離，則可以通過聲波飛行時間(Time-of-flight, TOF)來確定聲波傳播路徑上氣體介質的傳播速度，進而得到氣體介質溫度[5]：

(2)

式中：d為聲波傳播路徑距離；tTOF為聲波傳播路徑的飛行時間.

(3)

考慮測量噪聲，式(3)可表達成：

(4)

式中：rnoise為測量噪聲.

簡單地說，AT反問題的求解就是在已知W和b的條件下如何快速有效地求解式(4)中的x，再通過插值等數學方法得到整個溫度場信息.

2 重建算法

采用一種兩階段重建算法來改善重建質量.第一階段，重建區域被劃分成一系列粗的離散網格，其中的網格數少于獨立測量數據，選用ART方法獲得粗網格的溫度場.第二階段，在粗網格的溫度場數據基礎上，通過BP神經網絡預測得到細化后的溫度場信息.

2.1 ART方法

式(4)的求解是一個病態反問題，如何有效求解該方程對于AT的實際應用至關重要.ART方法[10-11]是一種求解病態反問題的有效方法.根據ART方法得到求解公式為：

(5)

式中：k為迭代步數；λ為松弛因子；Wi為系數矩陣W的第i行；bi為聲波TOF向量b的第i行.

2.2 BP神經網絡

BP神經網絡[16-17]是一種誤差逆傳播算法訓練的多層前饋網絡，其學習規則是最速下降法，利用反向傳播的方法調整網絡權重和閾值，使網絡的誤差平方和實現最小化.Hecht-Nielsen[18]證明了具有單隱層的三層前饋網絡可以處理任何多變量多項式函數.因此，筆者采用三層BP神經網絡來預測溫度場.

BP神經網絡模型由輸入層(Input Layer)、隱含層(Hidden Layer)和輸出層(Output Layer)組成.每層都由一定數量的神經元所組成.網絡通過不同層次的神經元實現互連，但是同層的神經元間沒有任何聯系.BP神經網絡的拓撲結構見圖1.

圖1 BP神經網絡的拓撲結構Fig.1 Topology of the BP neural network

(6)

式中：f(·)為傳遞函數；vj為隱含層的輸入；wji為輸入層和隱含層節點間的網絡權重；ui為輸入節點(網格中心點坐標)；θj代表閾值.

同樣，由傳遞函數得到對應的輸出層的節點輸出zt：

(7)

式中：Lt為輸出層的輸入；vtj為隱含層和輸出層節點間的網絡權重；γt代表閾值.

最終，輸出神經元的誤差E(n)可表述為：

(8)

式中：tt為輸出節點的期望值.

如果輸出誤差小于預設誤差，則訓練過程停止；反之，修改權重及閾值，直到誤差小于預設誤差值.BP神經網絡的訓練步驟如圖2所示.

與其他預測方法相比，BP神經網絡可以逼近任意的非線性映射關系，并且具有較好的泛化能力.因此，采用BP神經網絡來預測細化網格的溫度場.

圖2 BP神經網絡的流程圖Fig.2 Process of the BP neural network

2.3 重建步驟

綜上所述，重建算法的步驟總結如下：步驟1，重建區域被劃分為一系列粗的離散網格；步驟2，根據聲波TOF數據，采用ART方法重建區域的粗網格溫度場；步驟3，根據步驟2得到的粗溫度場數據，采用BP神經網絡預測細化后網格的溫度場.

根據上面的討論，將提出的重建方法簡稱為代數重建-神經網絡算法(ART-NN).

3 數值仿真及討論

通過Matlab R2013b軟件進行數值仿真，對多種溫度場進行重建，以驗證算法的可行性與有效性，并將重建結果與Tikhonov正則法、ART方法和Landweber迭代法的重建結果進行比較.

假設鍋爐爐膛截面為20 m×20 m的正方形區域，按圖3所示等距布置16個聲波收發器，考慮到收發器在同側墻壁之間不會產生明顯的有效信號，因此除去自身及同側墻壁的收發器影響，共形成96條有效的聲學傳播路徑.當其中一個收發器可以作為發射器時，其他的收發器作為接收器獲取聲波TOF數據.

圖3 聲波收發器布置圖Fig.3 Arrangement of the acoustic transceivers

3.1 仿真驗證1

采用單峰對稱溫度場來驗證ART-NN算法的可行性.從應用方面來看，一個成功的算法應該具有較好的魯棒性.因此，在計算獲得的TOF數據中添加一定的隨機噪聲信號(即均值為0，標準差為3.0×10-5).單峰對稱溫度場模型為：

T(x,y)=400exp{-[(x-10)2+(y-10)2]/450}+500exp{-[(x-10)2+(y-10)2]/ 18}+900

(9)

在參數選擇上，Tikhonov正則法的正則化參數選取0.01；ART方法的松弛因子為1，迭代步數選取1 000；Landweber迭代法的松弛因子為1，迭代步數為1 000；在ART-NN算法中，參數憑經驗選定，松弛因子為1，迭代步數為1 000，BP神經網絡選擇三層神經網絡，其中隱含層的神經元個數為200，隱含層和輸出層的傳遞函數分別為tansig和purelin，采用trainlm函數實現BP神經網絡的訓練.溫度場重建精度的評價指標由平均相對誤差Tave和均方根誤差Trms判定，二者定義[4,19]為：

(10)

(11)

圖4給出了單峰對稱溫度場模型和采用Tikhonov正則法、ART方法、Landweber迭代法和ART-NN算法的重建結果.表1為其重建誤差.

(a)溫度場模型

(b)Tikhonov正則法

(c)ART方法

(d)Landweber迭代法

(e)ART-NN算法圖4 單峰對稱溫度場重建Fig.4 Single-peak symmetrical temperature distribution reconstruction表1 單峰對稱溫度場重建誤差Tab.1 Reconstruction error of single-peak symmetrical temperature %

從圖4可以看出，與其他算法相比，ART-NN算法的溫度場重建質量較高.由表1可知，ART-NN算法的平均相對誤差和均方根誤差分別是1.29%和1.85%，表明ART-NN算法能夠應用于AT重建.

3.2 仿真驗證2

采用雙峰溫度場模型進一步評估ART-NN算法的有效性.其中算法參數和加入的隨機噪聲信號與3.1節相同.雙峰溫度場模型為：

T(x,y)=800exp{[-50(x-5)2-10(y-10)2]/300}+800exp{[-50(x- 15)2-10(y-10)2]/300}+1 000

(12)

圖5為雙峰溫度場模型和采用Tikhonov正則法、ART方法、Landweber迭代法和ART-NN算法的重建結果.表2為其重建誤差.

從圖5可以看出，Tikhonov正則法、ART方法和Landweber迭代法的重建結果并不理想.且從表2可以看出，這3種方法的平均相對誤差分別為4.00%、3.96%和5.50%，均大于ART-NN算法的平均相對誤差3.65%.因此，ART-NN算法的重建質量較高.

(a)溫度場模型

(b)Tikhonov正則法

(c)ART方法

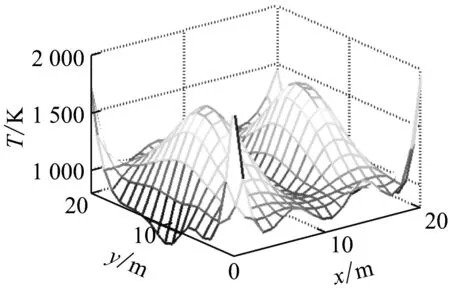
(d)Landweber迭代法

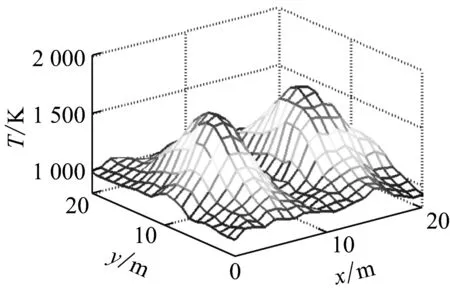
(e)ART-NN算法圖5 雙峰溫度場重建Fig.5 Double-peak temperature distribution reconstruction表2 雙峰溫度場重建誤差

Tab.2 Reconstruction error of double-peak temperature %

3.3 仿真驗證3

對多峰溫度場進行數值模擬.其中算法參數和加入的隨機噪聲信號與3.1節相同.多峰溫度場模型為：

T(x,y)=800exp{[-70×(x-6)2-30×(y-6)2]/300}+800exp{[-70×(x-6)2- 30×(y-14)2]/300}+800exp{[-70×(x-14)2-30×(y-6)2]/300}+800× exp{[-70×(x-14)2-30×(y-14)2]/ 300}+1 000

(13)

圖6給出了多峰溫度場模型和采用Tikhonov正則法、ART方法、Landweber迭代法和ART-NN算法的重建結果.表3為其重建誤差.從表3可以看出，Tikhonov正則法、ART方法和Landweber迭代法的平均相對誤差分別為7.22%、7.14%和8.68%，高于ART-NN算法的4.88%.這表明ART-NN算法是一種成功的求解AT反問題方法.

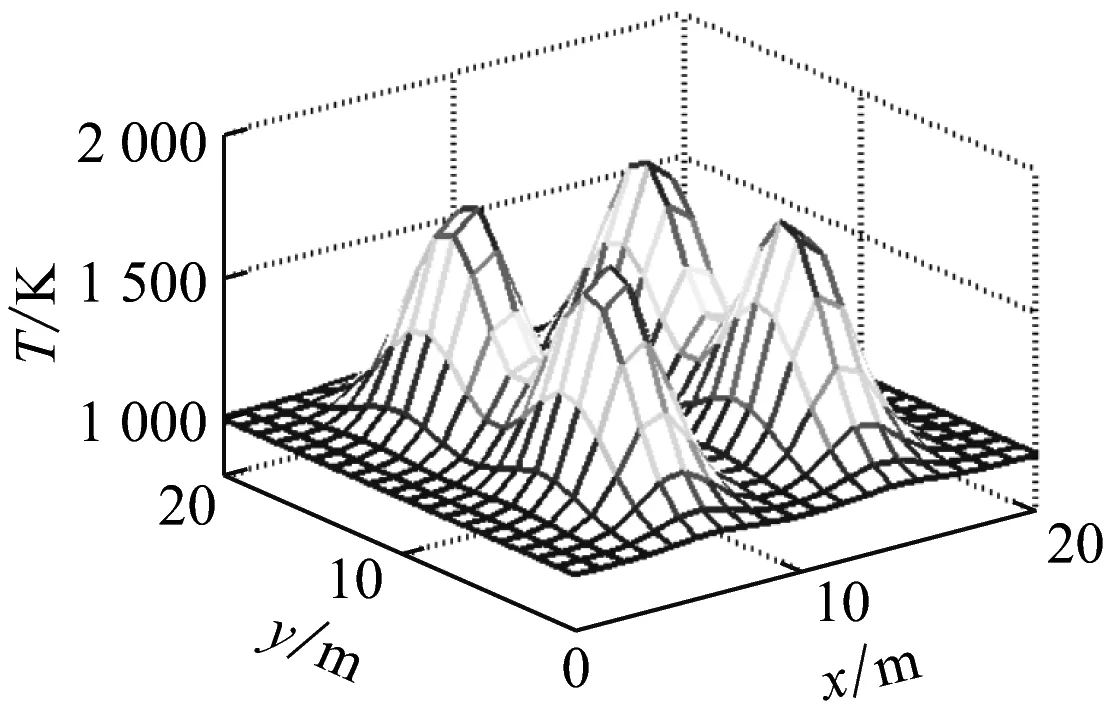
(a)溫度場模型

(b)Tikhonov正則法

(c)ART方法

(d)Landweber迭代法

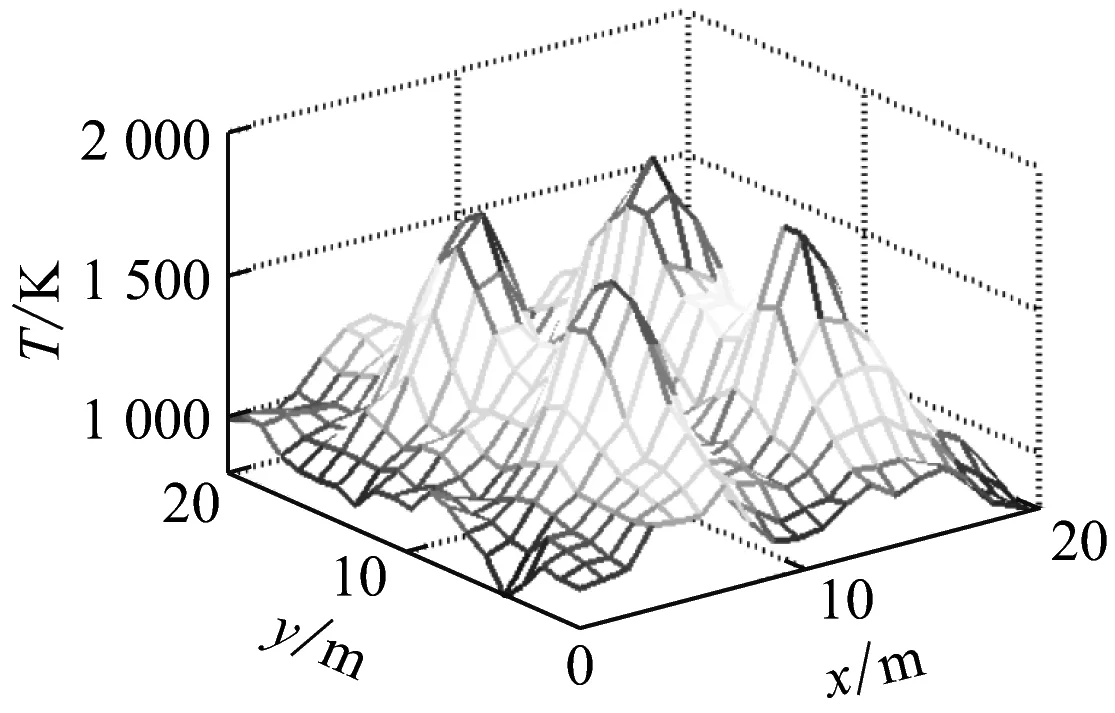
(e)ART-NN算法圖6 多峰溫度場重建Fig.6 Multi-peak temperature distribution reconstruction表3 多峰溫度場重建誤差Tab.3 Reconstruction error of multi-peak temperature %

3.4 仿真驗證4

由于真實鍋爐爐膛的溫度場是動態的，因此，筆者構建了一個動態的溫度場(見圖7 (a))，進一步驗證ART-NN算法的可行性與有效性.其中算法參數和加入的隨機噪聲信號與3.1節相同.選用三幀不同的溫度場T1→T2→T3來模擬動態溫度場，其溫度場模型分別為：

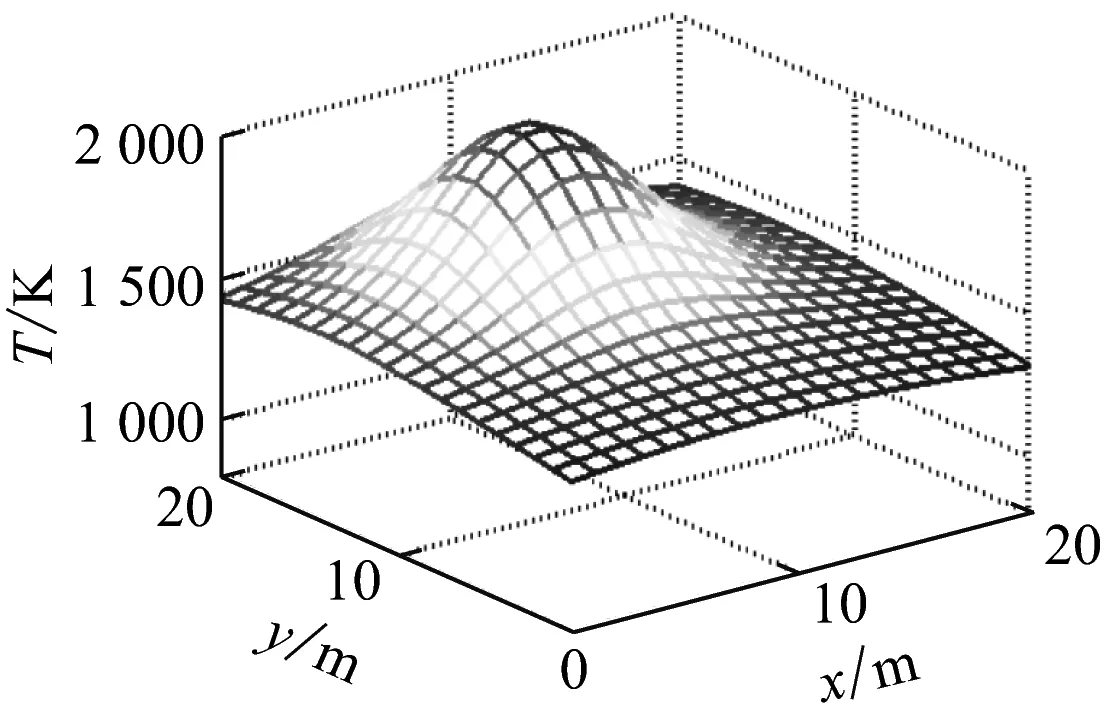
(a)溫度場模型

(b)Tikhonov正則法

(c)ART方法

(d)Landweber迭代法

(e)ART-NN算法圖7 動態溫度場重建Fig.7 Dynamic temperature distribution reconstruction

T1=300exp{-[(x-5)2+(y-8)2]/450}+ 400exp{-[x-5)2+(y-8)2]/18}+ 700

(14)

T2=400exp{-[(x-9)2+(y-14)2]/500}+500exp{-[(x-9)2+(y-14)2]/25}+ 1 100

(15)

T3=500exp{-[(x-16)2+(y-9)2]/350}+ 600exp{-[(x-16)2+(y-9)2]/10}+ 1 200

(16)

動態溫度場模型和采用Tikhonov正則法、ART方法、Landweber迭代法和ART-NN算法的重建結果如圖7所示.表4為其重建誤差.

表4 動態溫度場重建誤差

Tab.4 Reconstruction error of dynamic temperature %

從圖7和表4可以看出，與其他重建算法相比，ART-NN算法重建的平均相對誤差最小，分別為1.27%、1.24%和1.24%，證實了ART-NN算法能夠應用于動態溫度場重建問題.

綜上所述，ART-NN算法的溫度場重建結果要優于Tikhonov正則法、ART方法和Landweber迭

代法.就重建速度而言，從耗費時間的比較(見表5)可以看出，ART-NN算法的速度優于ART算法，但是劣于Tikhonov正則法和Landweber迭代法.

上述重建仿真研究都是在標準差為3.0×10-5的噪聲條件下進行.在本文中，筆者增加了不同噪聲水平的TOF數據進一步評估算法的可行性與有效性.噪聲水平η的定義如下：

(17)

式中：YO和YC分別代表真實的和噪聲污染的TOF數據；YC=YO+λω，其中λ代表標準差，ω代表均值為零，標準差為1的正態分布隨機數.

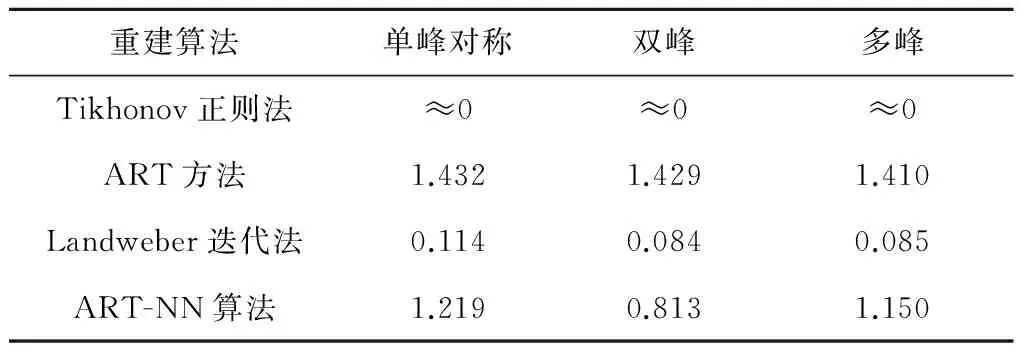
表5 耗費時間Tab.5 Reconstruction time s

圖8給出了噪聲水平在0.4%～4.5%區間時，ART-NN算法、Tikhonov正則法、ART方法和Landweber迭代法溫度重建的平均相對誤差.圖8中，ART-NN算法展示了良好的穩健性，重建溫度場的平均相對誤差在所有算法中最小.

然而，在圖8中也發現，隨著噪聲水平的增加，所有算法重建溫度場的平均相對誤差也在逐漸增加.這個結果表明，在實際的測量中，應該進一步改善TOF數據的測量質量.

(a)單峰對稱溫度場

(b)雙峰溫度場

(c)多峰溫度場圖8 不同噪聲水平下溫度場重建的平均相對誤差Fig.8 Mean relative errors of temperature distribution reconstruction at different noise levels

4 實驗驗證

筆者搭建了由聲波收發器、信號放大器、數據采集卡以及計算機組成的溫度場實驗裝置.在直徑為20.05 cm的圓形被測區域內均勻布置20個聲波收發器，在被測區域下方(距離被測層面約14 cm)放置300 W的電熱爐.考慮到實際測量和儀表等因素，選擇的采樣頻率為750 kS/s，采樣點數為每通道20 000點.

溫度場測量系統工作時，一個聲波收發器作為發射器發射聲波信號，對應側5個聲波收發器作為接收器接收聲波信號.數據采集系統測量5路接收信號，得到各聲波TOF測量值.程序設定間隔1.5 s后，切換到下一個聲波收發器，使之作為發射器，對應側5個聲波收發器作為接收器，依次類推，直到第20個聲波收發器已作過發射器后，結束測量并獲得全部TOF測量值.之后，采用ART-NN算法重建出被測區域的溫度場.結果如圖9所示，并通過表6給出了算法重建和實際熱電偶測量的相對誤差.

圖9 溫度場重建結果Fig.9 Temperature distribution reconstruction results表6 實驗溫度場重建誤差Tab.6 Reconstruction error of experimental results

位置坐標/cm熱電偶測量溫度/K聲學法重建溫度/K相對誤差/%(0,0)347.0353.21.79(-5.5,5.5)301.9293.42.82(5.5,5.5)304.7306.70.66(-5.5,-5.5)301.9295.52.12(5.5,-5.5)306.3296.33.26

從圖9和表6可以看出，ART-NN算法重建結果與實際熱電偶測量值相比，相對誤差值均小于3.26%，進一步證明了該算法的可行性與有效性.

5 結 論

(1)數值實驗比較結果發現，ART-NN算法的平均相對誤差和均方根誤差分別低于4.88%和6.48%，該重建結果優于Tikhonov正則法、ART方法和Landweber迭代法，證明該方法可以有效地提供爐內溫度場信息.

(2)ART-NN算法具有良好的穩健性，當測量數據不準確時仍能保持良好的重建精度.該特性有利于實際的工程應用，因為實際的測量數據總是包含了一定程度的噪聲.

(3)采用ART-NN算法進行實驗重建時，其重建結果與實際熱電偶測量值相比，相對誤差值均小于3.26%，證實了ART-NN算法的可行性與有效性.

[1] 沈國清, 吳志泉, 安連鎖, 等. 基于少量聲學數據的爐內溫度場重建[J]. 動力工程, 2007, 27(5): 702-706.

SHEN Guoqing, WU Zhiquan, AN Liansuo, et al. Reconstruction of temperature fields of furnace on the basis of few acoustic data[J]. Journal of Power Engineering, 2007, 27(5): 702-706.

[2] ZIEMANN A, ARNOLD K, RAABE A. Acoustic tomography in the atmospheric surface layer[J]. Annales Geophysicae, 1998, 17(1): 139-148.

[3] FAN Wei, CHEN C-T A, CHEN Ying. Calibration of an acoustic system for measuring 2-D temperature distribution around hydrothermal vents[J]. Ultrasonics, 2013, 53(4): 897-906.

[4] YAN Hua, CHEN Guannan, ZHOU Yinggang, et al. Primary study of temperature distribution measurement in stored grain based on acoustic tomography[J]. Experimental Thermal and Fluid Science, 2012, 42: 55-63.

[5] 沈雪華, 熊慶宇, 石欣, 等. 基于收發分體聲波換能器的二維溫度場重建[J]. 儀器儀表學報, 2015, 36(8): 1715-1723.

SHEN Xuehua, XIONG Qingyu, SHI Xin, et al. Two-dimensional temperature field reconstruction based on split type acoustic transducers[J]. Chinese Journal of Scientific Instrument, 2015, 36(8): 1715-1723.

[6] PILATO G, VASSALLO G. TSVD as a statistical estimator in the latent semantic analysis paradigm[J]. IEEE Transactions on Emerging Topics in Computing, 2015, 3(2): 185-192.

[7] LANDWEBER L. An iteration formula for fredholm integral equations of the first kind[J]. American Journal of Mathematics, 1951, 73(3): 615-624.

[8] 李芝蘭, 顏華, 陳冠男. 基于修正Landweber迭代的聲學溫度場重建算法[J]. 沈陽工業大學學報, 2008, 30(1): 90-93.

LI Zhilan, YAN Hua, CHEN Guannan. Acoustic temperature field reconstruction algorithm based on modified Landweber iterative method[J]. Journal of Shenyang University of Technology, 2008, 30(1): 90-93.

[9] 王善輝. 聲學層析成像反問題求解及溫度場重建算法研究[D]. 沈陽: 沈陽工業大學, 2014.

[10] 張順利, 張定華, 王凱, 等. 一種基于ART算法的快速圖像重建技術[J]. 核電子學與探測技術, 2007, 27(3): 479-483.

ZHANG Shunli, ZHANG Dinghua, WANG Kai, et al. A fast image reconstruction technique based on ART[J]. Nuclear Electronics & Detection Technology, 2007, 27(3): 479-483.

[11] BENDER M, DICK G, GE Maorong, et al. Development of a GNSS water vapour tomography system using algebraic reconstruction techniques[J]. Advances in Space Research, 2011, 47(10): 1704-1720.

[12] ANDERSEN A H, KAK A C. Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm[J]. Ultrasonic Imaging, 1984, 6(1): 81-94.

[13] ISAKOV V. Inverse problems for partial differential equations[M]. New York,USA: Springer, 1998.

[14] GILYAZOV S F, GOL′DMAN N L. Regularization of ill-posed problems by iteration methods[M]. Netherlands: Springer, 2000.

[15] GROETSCH C W. The Theory of Tikhonov regularization for fredholm equations of the first kind[M]. Melbourne: Pitman Publishing Pty Ltd, 1984.

[16] 朱凱, 王正林. 精通MATLAB神經網絡[M]. 北京: 電子工業出版社, 2010.

[17] 高建強, 王艷. 基于BP神經網絡的直接空冷凝汽器換熱性能預測[J]. 動力工程學報, 2013, 33(6): 443-447.

GAO Jianqiang, WANG Yan. BP neural network prediction on heat-transfer performance of direct air-cooled condensers[J]. Journal of Chinese Society of Power Engineering, 2013, 33(6): 443-447.

[18] HECHT-NIELSEN R. Theory of the backpropagation neural network[J]. Neural Networks, 1988, 1(S1): 445.

[19] 安連鎖, 王然, 沈國清, 等. 聲學CT算法重建爐內三維溫度場的仿真研究[J]. 動力工程學報, 2015, 35(1): 13-18.

AN Liansuo, WANG Ran, SHEN Guoqing, et al. Simulation study on reconstruction of 3D temperature field in boiler furnace by acoustic CT algorithm[J]. Journal of Chinese Society of Power Engineering, 2015, 35(1): 13-18.

Research on Temperature Distribution Reconstruction of a Boiler Furnace Based on Acoustic Tomography

LIUSha,LIUShi

(School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China)

To fast and acurately obtain the temperature distribution information in real-time monitoring of a boiler furnace, an ART-NN temperature distribution reconstruction algorithm was proposed for the acoustic tomography (AT) measurement by integrating the advantages of algebraic reconstruction technique (ART) and back propagation neural network (BPNN), which was subsequently used to reconstruct a variety of typical temperature distribution models, and then the reconstruction results and robustness were analyzed. Meanwhile, to further evaluate the performance of the proposed algorithm, experimental studies were conducted. Results show that both the reconstruction quality and the robustness of ART-NN algorithm are superior to that of the Tikhonov regularization, Landweber iteration and the ART method, which therefore may serve as a reference for quality improvement of temperature distribution reconstruction of boiler furnaces.

acoustic tomography; temperature distribution measurement; reconstruction algorithm; algebraic reconstruction technique; back propagation neural network

2016-06-12

2016-07-29

中央高校基本科研業務費專項資金資助項目(2016XS42)

劉 廈(1990-)，男，遼寧阜新人，博士研究生，研究方向為聲學法的溫度場重建算法及實驗研究.電話(Tel.):13260057499; E-mail：liusha031@163.com.

1674-7607(2017)07-0525-08

TK31

A

470.20