基于社交網絡的BA無標度演化模型的研究

◎王筱蕾

（西北政法大學 圖書館，西安 710122）

基于社交網絡的BA無標度演化模型的研究

◎王筱蕾

（西北政法大學 圖書館，西安 710122）

針對社交網絡中用戶間好友關系的特殊性，結合重啟特征和稀疏網絡平滑特征，提出了PageRank改進算法PRS；針對BA網絡模型的缺陷以及實際社交網絡的連接特性，將改進算法PRS作為擇優連邊考量因素之一，加入隨機連邊機制，構建了一種適合社交網絡的BA無標度網絡的改進模型。實驗證明，改進模型具有更優的網絡特性，適合構建與描述社交網絡。

PageRank算法；BA無標度網絡；社交網絡；改進模型

近年來，社交網絡因其發展迅速、用戶量巨大已成為最有影響力的信息交互平臺。掌握社交網絡的內部結構以及生長模式，對社交網站的建立與維護有著重要的理論指導意義。社交網絡作為復雜網絡的一個典型代表，其內部結構與生長特征都符合復雜網絡的特點。目前，多數研究者使用復雜網絡中的經典模型——BA無標度模型來描述社交網絡。然而，社交網絡因其自身特殊性，其節點具有多重連接方式且網絡特征參數多變。使用具有單一節點連接方式和網絡特征參數的BA無標度模型無法全面描述社交網絡[1]。針對這一問題，本文將借鑒BA無標度模型的構造算法以及網頁影響力排名算法PageRank，使用回顧性模擬的網絡建模方法，對傳統BA無標度模型進行，以期更全面準確的描述實際社交網絡的特征。

1 BA無標度模型算法介紹及缺陷分析

1.1 BA無標度模型算法

BA無標度網絡模型的構造算法[2]如下:

（1）增長：在一個具有m0個節點的網絡中，依次連入新節點，直到新節點被連接到已存在的m個節點上，這里m≤m0。

（2）擇優連接：單個已存在的節點i和單個新節點，它們能被連接到一起的概率∏（ki）與j節點的度kj以及i節點的度ki之間滿足以下關系：

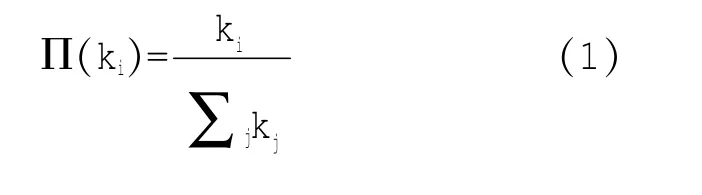
1.2 缺陷分析

首先，連接機制選擇。BA無標度網絡模型的連接機制考慮的是擇優連接，然而在實際網絡中節點之間的連接機制不僅僅為擇優連接，還存在隨機連接，例如，在社交網絡中，用戶在添加好友時除了會優先選擇一些好友以外，還會隨機添加一些感興趣的陌生人，因此在構造社交網絡模型時必須考慮到隨機連接這一條件。

其次，擇優連接的條件。BA無標度網絡模型的擇優連接機制中考慮的是節點的度數，即度越大，被選擇連接的可能性越大，在社交網絡中，每個節點就是用戶，節點的度就是用戶的好友數目，因此，BA無標度網絡模型的連接條件在社交網絡背景下就是用戶傾向于與好友數目較多的用戶建立連接，顯然這一觀點是片面的，在實際的社交網絡中，用戶除了會選擇好友數目多的用戶建立連接外，用戶的影響力也是十分重要的因素，如新浪微博中有一個名人影響力排名，通過一定的算法算出網絡上的名人影響力，并對其排名，一般用戶會根據影響力的大小選擇與其建立連接。因此，在構造社交網絡模型時，擇優連接中應當考慮到影響力因素。

2 基于社交網絡的BA無標度演化模型

2.1 PageRank算法介紹及改進

經典網頁排名PageRank算法為每個網頁設定PR值為網頁的影響力分數，借鑒PageRank算法的思想來對社交網絡中每個用戶進行影響力估算[3]，為了更準確地計算用戶的影響力，筆者對原PageRank算法進行改進，使用改進的PageRank算法來計算社交網絡中用戶的影響力大小。

2.1.1 PageRank算法介紹

PageRank算法[4]又稱網頁排名算法，是Google搜索引擎中的重要算法。算法思想是：當網頁A有一個鏈接指向網頁B時，就認為網頁B獲得了一定的分數，該分值的多少取決于網頁A的重要程度，即網頁A的重要性越大，網頁B獲得的分數就越高。由于網頁上的鏈接相互指向的復雜程度，該分值的計算過程是一個迭代過程，最終網頁將依照所得的分數進行排序并將結果送交給用戶，這個量化了的分數就是PageRank值。

要計算網頁A的PR值，就得利用指向它的網頁Ti的PR值，這就導致要求解一個巨大的方程組，然而復雜網絡中的結點是非常多的，求解這個方程組往往不現實的[5]。針對這一問題，筆者引入馬爾科夫假設，結合重啟特征與平滑特征，給出經典PageRank算法的求解方法：

Step1.由網絡鄰接矩陣A經過行歸一化得到矩陣W；

Step2.確定PageRank初始向量p0的值；

Step3.反復迭代經典PageRank算法計算公式pt+1，直到pt和pt+1的夾角余弦小于某一個小的閾值ε時停止；

Step4.pt即是各個結點的重要性向量，對其按照從大到小的順序排序，就可以得到節點重要性的排序結果。

2.1.2 PageRank算法改進

傳統的PageRank算法存在以下兩個問題：

（1）實際中存在用戶回退瀏覽不同頁面的情況，這個因素不應該被忽略，而上面原始的計算PR值公式并沒有考慮到這一點。

針對這一問題，筆者將引入一個較小的系數d，作為重置系數，并結合經典PageRank算法給出計算公式。用戶在網上瀏覽網頁時，可能會以某個概率跳轉到下一個頁面，當然也可能會回到上一個頁面。不妨假設用戶在每一次瀏覽網頁時都可能會以一定的概率去瀏覽當前頁面的鄰居，還會有一定的概率回到初始瀏覽的網頁，所以對于向量p，改為如下定義：

其中，d是一個介于0到1之間的常數，叫做重啟系數，即沖浪者以d的概率回到原點，并且d∈（0，1]；p0表示初始向量。從上式可以看出，用戶每次跳轉網頁時都會以概率d回到原始的網頁，或者按照概率去跳轉到其他網頁。對于復雜網絡而言，重啟特征會使得PageRank算法更加精準。

（2）網頁之間的鏈接的數量相比互聯網的規模非常稀疏，因此計算網頁的網頁排名也需要對零概率或者小概率事件進行平滑處理。

針對這一問題，筆者將引入一個很小的系數c，作為平滑處理系數。對于互聯網網絡而言，網頁結點之間鏈接的數量相比互聯網節點的規模比較稀疏，社交網絡中，用戶的連接關系數目較網絡節點規模也十分稀疏。因此計算網頁的網頁排名也需要對零概率或者小概率事件進行平滑處理。由于網頁的排名是個一維向量，對它的平滑處理可以利用一個小的常數c，表達如下：

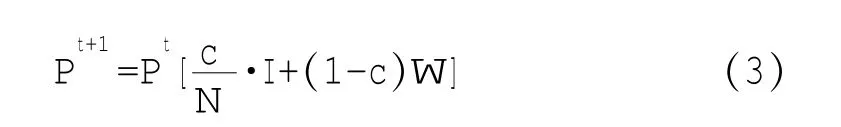
其中，N表示互聯網網頁的數量，c是一個介于0到1之間的常數，稱為平滑系數，I是單位矩陣。上式通過平滑系數c，來對零概率或者小概率事件進行平滑。

綜合以上兩個特征，筆者將以上改進算法PRS計算過程總結如下：

Step1.由網絡鄰接矩陣A經過行歸一化得到矩陣W；

Step2.確定PRS初始向量p0的值；

Step4.pt即是各個結點的重要性向量，對其按照從大到小的順序排序，就可以得到結點重要性的排序結果。

2.2 演化模型構建思想

前面介紹了BA無標度網絡模型的算法，并分析了該算法應用到社交網絡中的缺陷，針對該缺陷以及社交網絡的實際特征來構建適合描述社交網絡的演化模型。

首先，BA無標度網絡模型的連接機制是擇優連接，然而在實際的社交網絡中，用戶選擇好友并不總是擇優選擇[6,7]，除了有選擇性的添加好友以外還會隨機的添加一些陌生人作為好友，也就是存在一定概率的隨機選擇，因此應當設置一個參數p(0≤p≤1)，p表示用戶擇優選擇的概率，那么1-p則表示用戶隨機選擇的概率，p=0時表示網絡中所有用戶的連接全部都為隨機連接，p=1則表示網絡中所有用戶的連接全部都為擇優連接。

其次，在BA無標度網絡模型的擇優連接中是以節點的度作為衡量標準，節點的度越大，越容易與其他節點建立連接，在社交網絡中就是指一個用戶傾向于選擇好友數多的用戶來建立好友關系，客觀地說，這一觀點是片面的，實際上用戶選擇好友的標準不僅僅看一個用戶的人氣，影響力也是不容忽視的一個因素，用戶傾向于選擇人氣高或者影響力大的用戶來建立好友關系。在考慮影響力時，這里利用改進的PageRank算法PRS，將社交網絡中的每個用戶視為因特網中的每個網頁，像對每個網頁投票一樣為每個用戶投票，并設置PRS值，PRS值越高表示該用戶的影響力越大。算法開始時，為每個用戶分配一個相同的PRS值，然后進行迭代計算，每個用戶把自己的PRS值平均的分配給與其有連接關系的好友，然后每個用戶根據所得的權值進行求和，以此來對每個用戶的PRS值進行更新，在每一輪計算中用戶的PRS值都會更新，直到算法結束。因此，設置參數a(0≤a≤1),a表示用戶選擇人氣高即好友數多的用戶來建立好友關系，1-a表示用戶選擇影響力大的即PRS值高的用戶來建立好友關系。當a=0時表示網絡中的用戶在擇優選擇時只以影響力作為衡量標準，只選擇影響力大的用戶來建立好友關系。當a=1時表示網絡中的用戶在擇優選擇時只選擇人氣高的用戶來建立好友關系，也就是BA無標度網絡中的擇優連接思想。

另外，在實際的社交網絡中存在不同的社群，同一社群中的用戶聯系相對比較緊密，具有較大的聚類系數以及較小的平均路徑長度，而沒在社群中的用戶則可能互相聯系較少、聚類系數較小且平均路徑長度較大。然而普通的BA無標度網絡模型的聚類系數以及平均路徑長度是固定的，無法綜合的描述實際社交網絡的多種情況，因此需要一種具有可變聚類系數和可變平均路徑長度的模型來描述實際的社交網絡。通過調節參數p，a，我們可以控制隨機連接和擇優連接，以及擇優連接中度數和影響力的比例。

2.3 演化模型構建算法

（1）增長：在一個具有m0個節點的網絡中，依次連入新節點，直到新節點被連接到已存在的m個節點上，這里m≤m0。

（2）擇優選擇：一個新節點與網絡中已有的節點相連接，且選擇節點i概率與節點度成正比，即

選擇這種操作的概率為a，這里將a記為度指數；

新節點與網絡中已有的節點相連接，且選擇節點i概率與節點的影響力（PRS值）成正比，即

選擇這種操作的概率為1-a。

這里假設擇優選擇的選擇概率為p，將p記為擇優指數。

（3）隨機選擇：在已有網絡中隨機選擇一個節點與新節點連接。隨機選擇的選擇概率為1-p。

在改進模型構造算法中，任意兩點之間的距離為1，且連邊總是由老節點指向新節點，所以改進模型為有向無權網絡。所引入的兩個參數p和a都是可以調節的，當p=1且a=1時，改進模型退化為基本的BA無標度網絡模型。

在改進模型中，新節點以概率a隨機選擇網絡中的已有節點進行連接，以概率1-a進行擇優選擇，在擇優選擇中，以概率p選擇度數大的節點進行連接，以概率1-p選擇影響力高(即PRS值大)的節點進行連接。

3 .仿真結果

采用Matlab R2013a在Windows7環境下模擬仿真改進模型的網絡生成過程，并編程得出模擬網絡的度分布示意圖，并調整參數得出不同條件下的平均路徑長度、聚類系數變化圖。

3.1 度分布

對于改進模型的度分布，我們設計了三組不同的實驗，當參數取不同值時，來驗證生成網絡的度分布是否符合冪律分布。每組實驗的設計思想是，固定一個參數，使另外兩個參數兩兩變化，觀察度分布圖形，然后改變固定的參數，再觀察度分布圖形。在第一組實驗中，分別設置d=0.2和d=0.6得到圖1、圖2中的雙對數坐標下的改進模型度分布圖。在兩個圖中使用符號“*”表示a=0.1，p=0.2時的度分布圖，命名為A分布；使用符號“+”表示a=0.5，p=0.2時的度分布圖，命名為B分布；使用符號“o”表示a= 0.1，p=0.6時的度分布圖，命名為C分布。

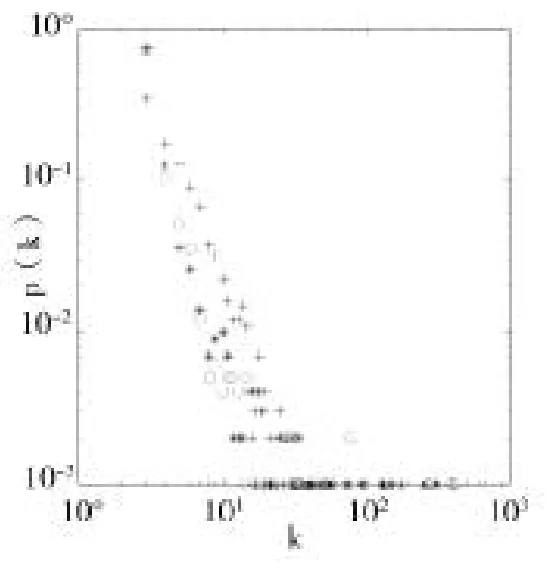
圖1 d=0.2時改進模型度分布

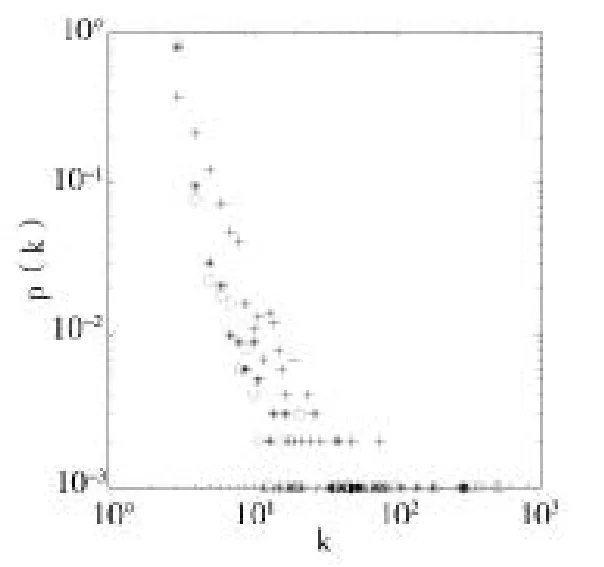
圖2 d=0.6時改進模型度分布

在這組實驗中，以上兩圖中B分布與A、C分布稍有差異，也就是說，當a取0.1時，度較大的節點數較多，當a取0.6時，度較小的節點數較多。

在第二組實驗中，分別設置a=0.2和a=0.6得到圖3、圖4中的雙對數坐標下的改進模型度分布圖。在兩個圖中使用符號“*”表示d=0.1，p=0.2時的度分布圖，使用符號“+”表示d=0.5，p=0.2時的度分布圖，使用符號“o”表示d=0.1，p=0.6時的度分布圖。

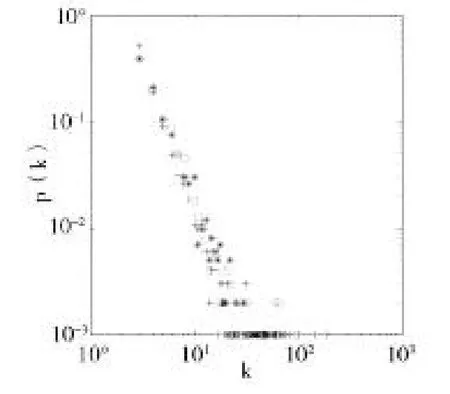
圖3 a=0.2時改進模型的度分布

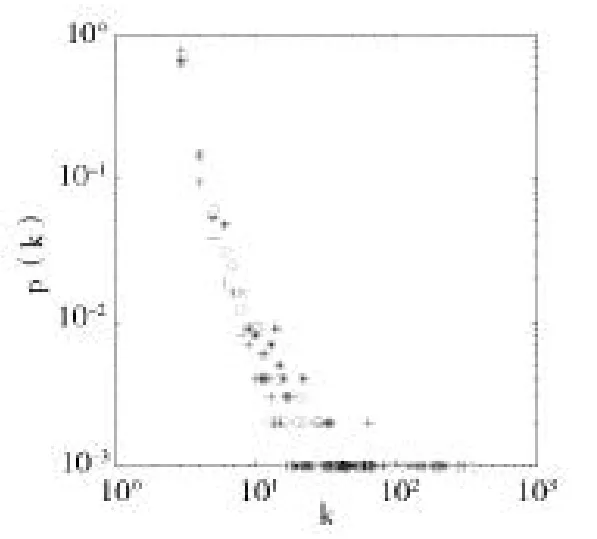
圖4 a=0.6時改進模型的度分布

在這組實驗中，從以上兩個圖可以看到改變a值的大小，度分布圖的形狀有變化，a取0.2時三種不同情況的度分布可擬合的直線斜率略大于a取0.6時。

在第三組實驗中，分別設置p=0.2和p=0.6得到圖5、圖6中的雙對數坐標下的改進模型度分布圖。在兩個圖中使用符號“*”表示d=0.1，a=0.2時的度分布圖，使用符號“+”表示d=0.5，a=0.2時的度分布圖，使用符號“o”表示d=0.1，a=0.6時的度分布圖。

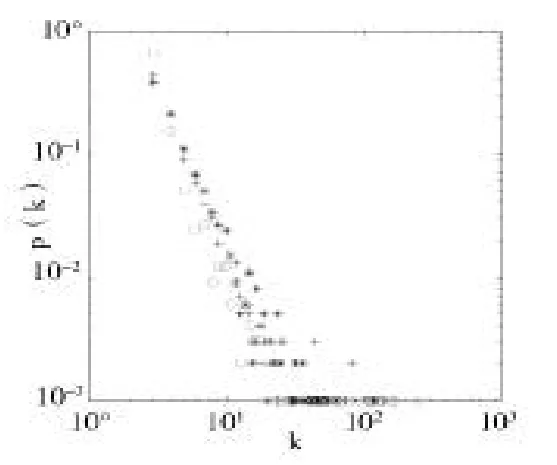
圖5 p=0.2時改進模型的度分布

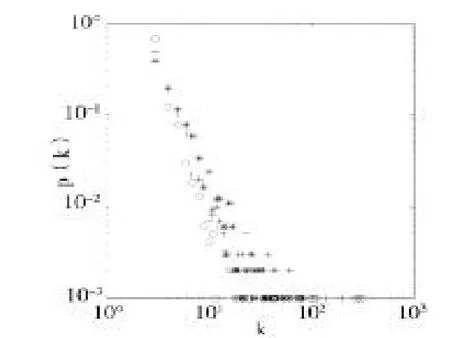
圖6 p=0.6時改進模型的度分布

在這組實驗中，由以上兩圖的度分布可以看到，p值取0.6時，度分布較為均勻，度數小的節點出現的概率較p取0.2時多一些，度數大的節點出現的概率較p取0.2時少一些。

由以上的6張圖可以看到，在取不同的參數下，改進模型都呈現出冪律分布，與BA模型一樣具有“胖尾”特征，不同之處在于，度數的大小與出現的概率大小不一致。也就是說，在改進模型中，隨機選擇與擇優選擇的比重以及擇優選擇采用哪種方式均不會影響模型的度分布特征。

3.2 聚類系數與平均路徑長度

以上的節點度分布圖說明了改進模型與BA模型一樣具有冪律特征，為了進一步分析改進模型的網絡特征，我們還對該網絡模型的聚類系數以及平均路徑長度進行了仿真，分別設置不同的參數取值來對比分析。由于d、a、p的值均在0到1之間，這里d和p我們分別去三個值：0.1、0.5、0.9，a從0.1取到0.9，得到不同的聚類系數與平均路徑長度。

分別選取d和p值為0.1、0.5、0.9，a從0.1取到0.9，作出不同參數取值時改進模型的聚類系數和平均路徑長度。圖7到圖9分別為d取0.1、0.5、0.9時改進模型的聚類系數變化圖。

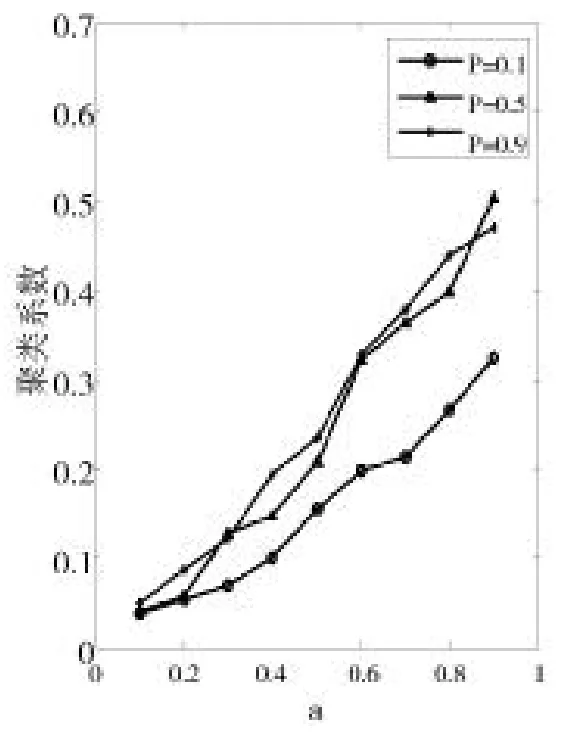
圖7 聚類系數(d=0.1)

圖8 聚類系數(d=0.5)

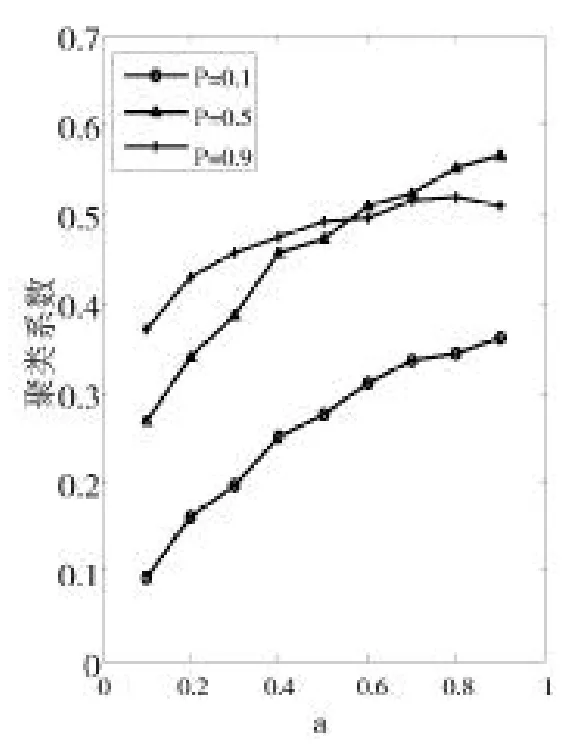
圖9 聚類系數(d=0.9)

觀察以上三圖，圖7和圖8中聚類系數總體會隨著a值的增加呈上升趨勢，而圖9中聚類系數的變化趨勢與前面兩圖有所不同，紅色折線（p=0.9）在a=0.5之后趨于平穩，說明在d和p取得較大值0.9的情況下，當a取值大于0.5時，聚類系數不再逐漸增加而是趨于一個相對平穩的值。因為當d，p，a同時取得較大值時，用戶之間進行連接時，隨機因素削弱，用戶影響力得分逐漸取決于固定的舊好友的PRS值，這使得連接方式趨于固定，因此，聚類系數逐漸趨于平穩。

圖10到圖12分別為d取0.1、0.5、0.9時改進模型的平均路徑長度變化圖。

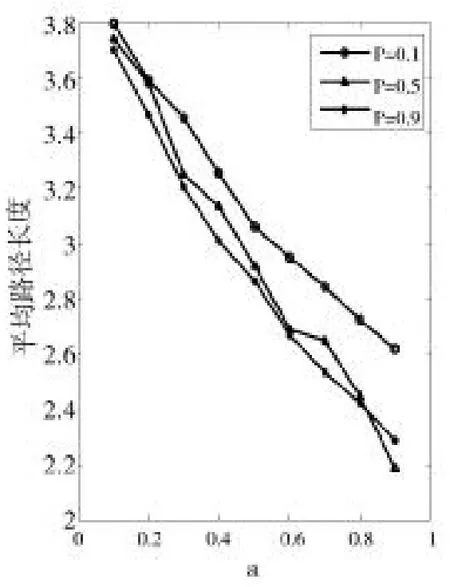
圖10 平均路徑長度(d=0.1)

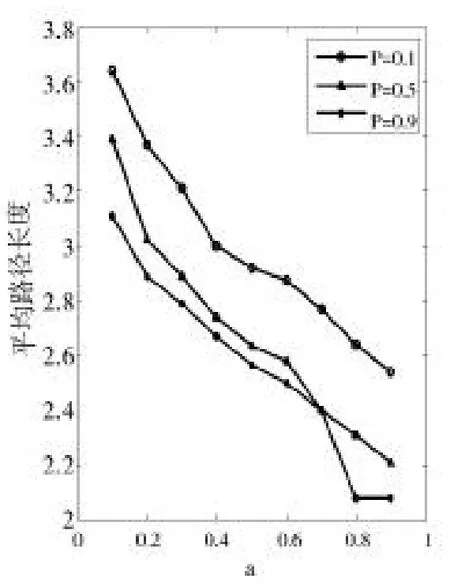
圖11 平均路徑長度(d=0.5)

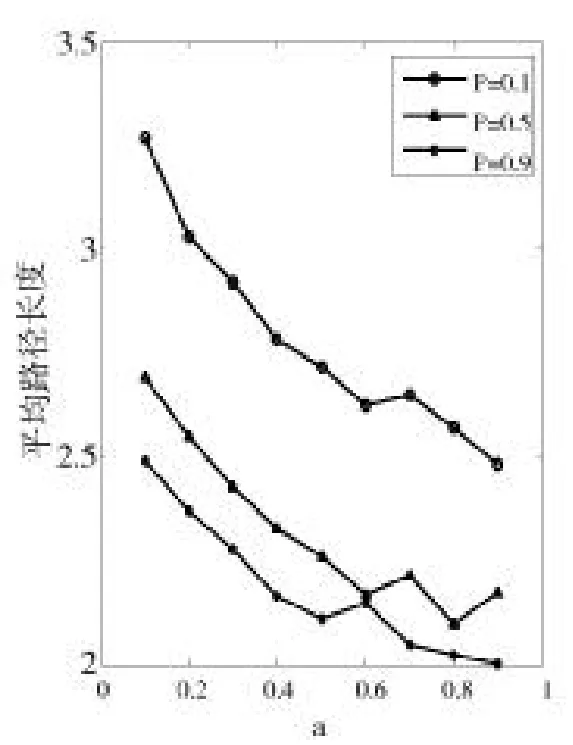
圖12 平均路徑長度(d=0.9)

3.3 實驗結果分析

（1）筆者改進BA模型聚類系數和平均路徑長度可調控范圍較大。聚類系數隨著可變參數d、a、p的增大成增大趨勢，而平均路徑長度成減小趨勢，這是目前的一些BA改進模型所不及的。筆者的模型更能滿足現實社交網絡的需求，因為在實際社交網絡中存在社群，當我們在研究不同范圍內的網絡特征時，其中的社群規模及數目也不同，有的網絡中社群規模較大，則它的聚類系數相對較大，平均路徑長度相對較小。

（2）筆者改進BA模型的平均路徑長度與原始BA模型相比總體偏小，而聚類系數偏大。在社交網絡中，從聚類系數的大小可以看出社團朋友圈的聚集程度，聚類系數越大表示聚集程度越高，越適合描述熟人網絡。在熟人網絡中，人們之間的信任度相對較強，傳播信息可信度較高。正是因為改進模型的聚類系數增大，因此它的平均路徑長度也減小到了合理的范圍之內，符合復雜網絡理論中的小世界網絡特征。

4 結束語

筆者針對BA無標度網絡模型的缺陷以及實際社交網絡的連接特性，提出了一種適合社交網絡的BA無標度網絡的改進模型，該模型基于多因素且具有混合連邊方式，考量節點連接概率方面，在擇優連接的基礎上增加了隨機連接，擇優連接的因素不僅只是節點的度還由節點的影響力來決定。仿真結果顯示，該模型的度分布呈冪律分布，通過調節參數值可大范圍調節聚類系數及平均路徑長度，比原始BA模型具有更優的統計特性，適合構建與描述具有大聚類系數特性的社交網絡,為構建不同需求的網絡提供了一種較為靈活的方案，具有普適性。

[1]侯麗芳.無標度網絡的演化模型研究及應用[D].秦皇島：燕山大學,2016.

[2]DL Wang,Z G Yu,Anh V.Multifractal analysis of complex networks[J].Chinese Physics B,2012(8): 89-99.

[3]李志宏,莊云蓓.基于PageRank算法的雙維度微博用戶影響力實時度量模型[J].系統工程,2016(2):128-137.

[4]Page L,Brin S,Motwani R,et al.The PageRank citation ranking:bringing order to the web[EB/OL].http: //ilpubs.stanford.edu:8090/422/.2012-05-13.

[5]張琨,李配配,朱保平,等.基于PageRank的有向加權復雜網絡節點重要性評估方法[J].南京航空航天大學學報,2013(3):429-434.

[6]王金龍.在線社交網絡模型演化及傳播機制研究[D].濟南：山東師范大學,2016.

[7]許進,楊揚,蔣飛,等.社交網絡結構特性分析及建模研究進展[J].中國科學院院刊,2015(2):216-228.

（責任編輯 卞建寧）

Study on BA Scare-free Evolving Model Based on Social Network

WANG Xiaolei
(Northwest University of Political Science and Law Library,Xi’an,710122,China)

TP311

B

1671-9123（2017）02-0133-07

2017-03-30

王筱蕾（1989-），女，陜西眉縣人，西北政法大學圖書館助理館員。