星載相機隔振器的結構優化和隔振性能分析

劉世平 熊 琦 李世其 王 躍

1.華中科技大學機械科學與工程學院，武漢，4300742. 北京空間機電研究所，北京，100076

?

星載相機隔振器的結構優化和隔振性能分析

劉世平1熊 琦1李世其1王 躍2

1.華中科技大學機械科學與工程學院，武漢，4300742. 北京空間機電研究所，北京，100076

基于黏彈性材料在剪切力作用下產生較大阻尼損耗的原理，初步設計了一種星載相機隔振器。采用正交試驗設計結合有限元分析的方法，詳細探究了隔振器的結構參數對其固有頻率和模態損耗因子的影響，據此對隔振器的結構進行優化。建立了相機隔振系統的有限元模型，并對其進行了力學強度校核和隔振性能分析,結果表明，使用該隔振器的相機隔振系統能滿足衛星發射階段的力學環境要求，并具有較好的隔振效果。

隔振器；正交試驗設計；結構優化；隔振系統

0 引言

星載相機在發射至預定軌道的過程中，會受到多種靜態載荷和動態載荷的影響，如過載、熱載、振動和噪聲等，力學環境相當惡劣。從頻譜分布來看，環境載荷包含幾十赫茲的低頻結構振動、幾百到幾千赫茲的中高頻隨機振動和聲激振動。據調查，45%的衛星發射失敗是由發射階段的振動造成的[1-3]。傳統的設計方法往往以加大體積和重量的代價來換取衛星平臺和相機的穩定性，這與航天器的小型化、輕量化、精密化發展趨勢相矛盾。解決上述問題的一個有效方法是依據相機結構的動力學性能及衛星平臺的擾動環境，研制出相機專用高性能隔振器及隔振系統，使相機在火箭發射時的強烈振動下不會損壞，為其穩定地工作提供保障[4-6]。

本文對結構形式初定的相機隔振器采用正交試驗設計結合有限元分析的方法，詳細探究其幾種結構參數對振動特性的影響，根據隔振系統的力學強度和隔振性能要求，對隔振器的結構進行優化。用優化后的隔振器組成相機隔振系統并進行模態、靜力過載以及諧響應等計算，分析相機隔振系統的力學強度和隔振性能。

1 相機隔振器和隔振系統

相機隔振器就是安裝在衛星平臺與相機之間具有特定彈性和阻尼性能的裝置，它可阻隔并減弱發射過程中振動能量的傳遞。相機隔振器的隔振性能常用振動傳遞率T來描述，單個隔振器的力學模型可簡化為圖1所示模型[7]。圖1中，k為隔振器的剛度；c為隔振器的阻尼系數；m為被隔振物體的質量；q(t)為被隔振物體的響應；Q(t)為系統受到的激勵。

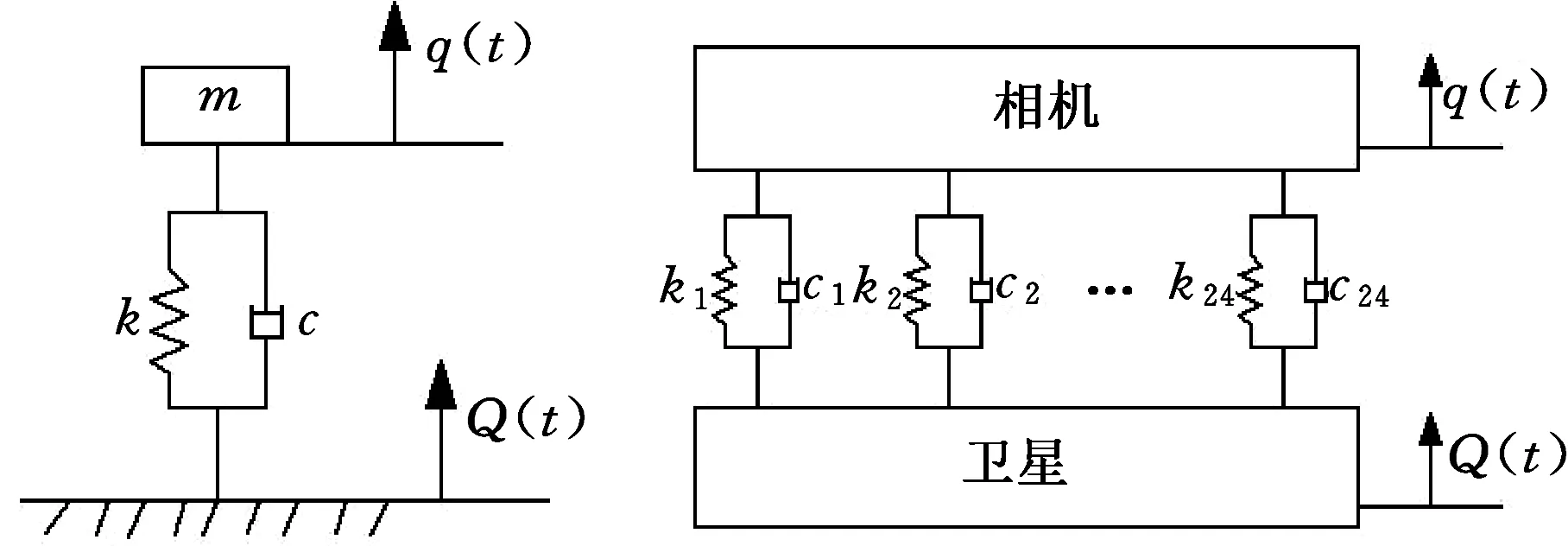
圖1 隔振器力學模型 圖2 隔振系統力學模型Fig.1 Mechanical model of isolator Fig.2 Mechanical model of vibration isolation system

一系列隔振器按一定布置方式排列就組成了隔振系統，其力學模型可以簡化為圖2所示模型，其隔振性能同樣可用振動傳遞率T來描述。簡化成單自由度隔振系統的振動傳遞率

(1)

ξ=c/cnλ=ω/ωn

式中，cn為臨界阻尼系數;ωn為隔振系統的固有頻率；ω為激勵頻率；ξ為阻尼比，隔振系統需滿足T≤4，由式(1)可得阻尼比ξ≥0.13。

相機隔振系統負載質量m為1300 kg，縱向固有頻率要大于35 Hz，根據

(2)

可得,縱向剛度Kz要大于62.87kN/mm，整個系統包括24個隔振器，故每個隔振器的縱向剛度要大于2.62kN/mm。

相機隔振器的結構如圖3所示，由金屬支架和阻尼材料組成，金屬支架輪廓為跑道形，中間有交錯排列的剪切齒，外部由阻尼材料包裹，金屬支架依據等強度理論采用變厚度設計，該設計可以大幅提高金屬支架受力均勻性，顯著降低應力水平。金屬支架受力時，中間的剪切齒會充分剪切阻尼材料，形成大阻尼特性，產生較大的阻尼損耗。

圖3 相機隔振器結構圖Fig.3 Structure diagram of camera isolator

金屬材料選用牌號為TC4的鈦合金，它具有良好的抗蝕性、比強度，優良的疲勞抗力、斷裂韌性和塑性；阻尼材料以丁基橡膠為基體，并添加了適量的填充劑、補強劑等配制而成，具有較好的綜合性能。采用動力熱機械分析(DMA)實驗測得的阻尼材料的平均損耗因子為0.677，由于黏彈性材料在低頻共振時存在損耗因子是阻尼比2倍的線性關系，因而隔振器滿足阻尼比ξ≥0.13。

相機隔振系統由24個沿圓周均勻分布的隔振器以及中部法蘭、上筒、下筒、配重等組成，整體模型如圖4所示。

圖4 相機隔振系統模型圖Fig.4 Model diagram of camera vibration isolation system

2 隔振器的結構優化

約束阻尼層結構受力時約束層和阻尼層之間發生剪切變形，從而產生阻尼耗能，增大約束層和阻尼層的接觸面積以及改變阻尼材料的形狀,這可能會影響結構的振動特性。

本文將豎直剪切齒末端的凸臺擴展為水平剪切齒，并分析水平傾斜角度對系統固有頻率和模態損耗因子的影響。在阻尼層數、阻尼層厚度以及約束層厚度相同的條件下，計算無水平剪切齒以及水平傾斜角度α分別為0°、15°、30°、45°時的固有頻率和模態損耗因子，圖5所示依次為無水平剪切齒、水平傾斜角度為0°、30°時的有限元模型，固有頻率和模態損耗因子計算結果如圖6所示。

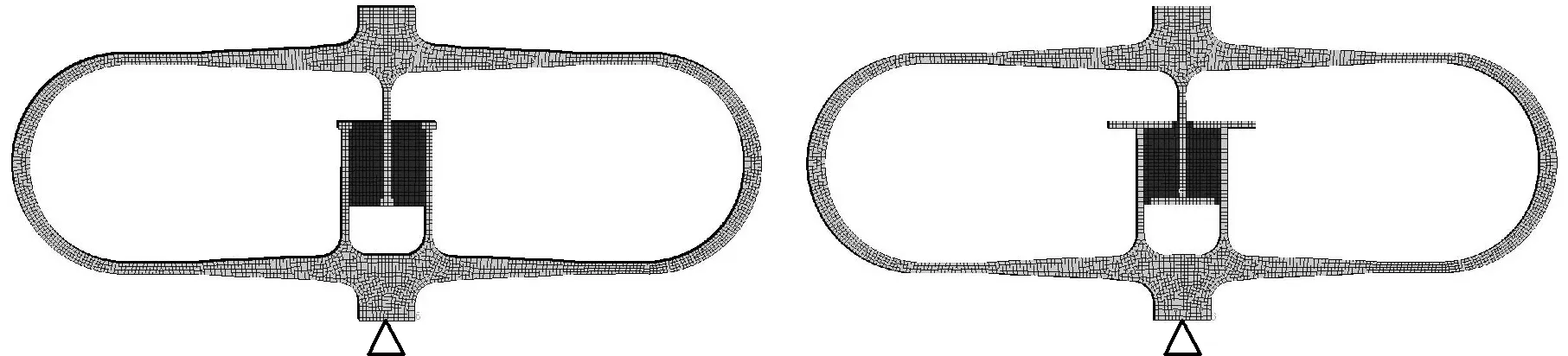
(a)無水平剪切齒 (b)α=0°

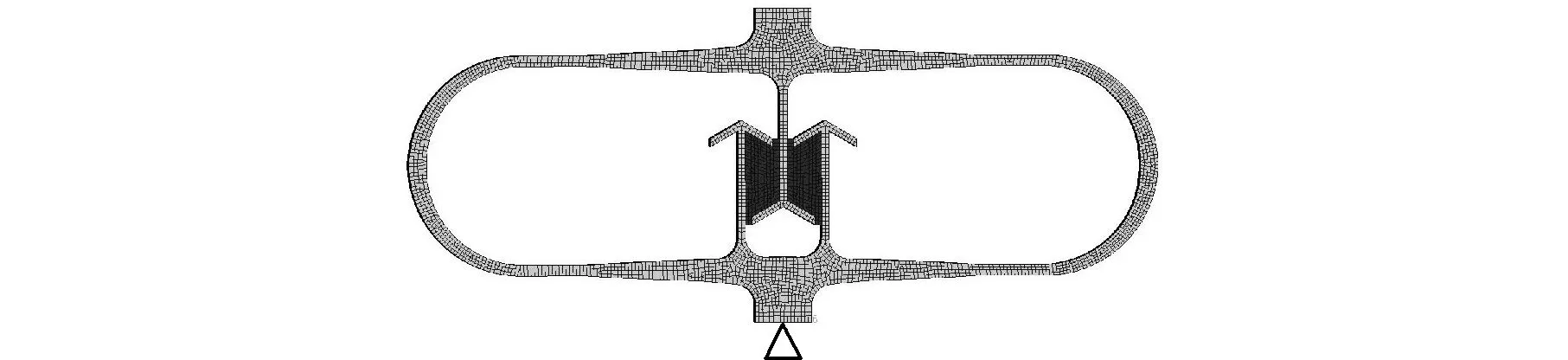
(c)α=30°圖5 不同水平剪切齒的隔振器有限元模型Fig.5 Finite element model of isolator with different horizontal shear teeth

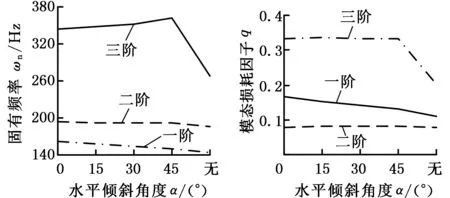
(a)對固有頻率的影響 (b)對模態損耗因子的影響圖6 水平剪切齒對固有頻率和模態損耗因子的影響Fig.6 Influence of horizontal shear teeth on natural frequencies and modal loss factors

由圖6可知，增加水平剪切齒后隔振器第一階、第二階模態頻率和損耗因子有一定的提高，第三階模態頻率和損耗因子增大顯著，但傾斜角度大小的影響不太明顯。

隔振器的前兩階振型分別是上下支架在X軸和Y軸方向上的擺動，是對阻尼材料的橫向拉扯；第三階振型是上下支架在Z軸方向上的拉壓，是對阻尼材料的縱向拉扯。由于第三階模態阻尼比大于第一階、第二階模態阻尼比，因此，隔振器的阻尼效果主要體現在縱向，即縱向是其主隔振方向。

選擇具有水平剪切齒的隔振器，繼續探究阻尼層厚度D、水平約束層厚度d1、豎直約束層厚度d2、阻尼層數n共4個結構參數對隔振性能的影響，采用正交試驗設計的方法設計優化方案，結構參數見圖7。

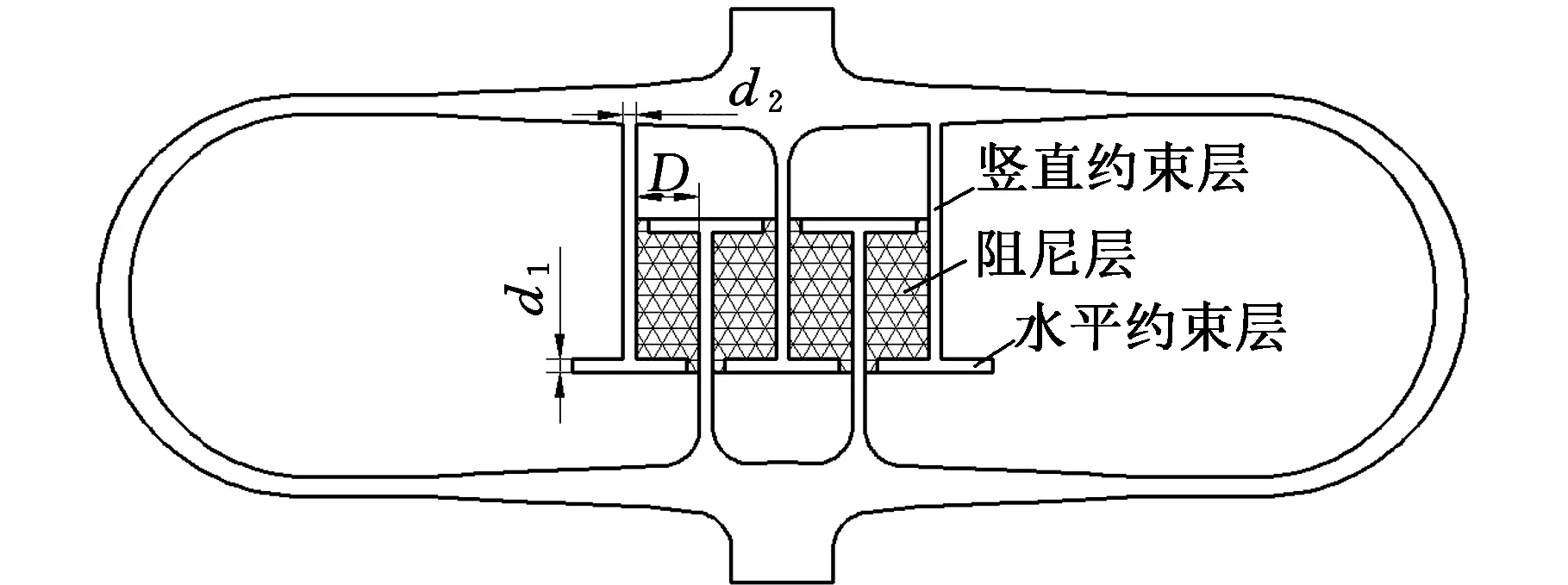
圖7 相機隔振器截面模型Fig.7 Section model of camera isolator

正交試驗設計是解決多因素、多水平和具有隨機誤差的試驗問題的一種優化方法，在確定了因素和水平后，選擇合適的正交表來安排試驗，最后對數據結果進行直觀分析和方差分析[8-9]。本文的試驗中含有4個因素，每個因素含有三種水平，見表1，因此選擇四因素、三水平的L9(34)正交試驗表，試驗組合見表2。

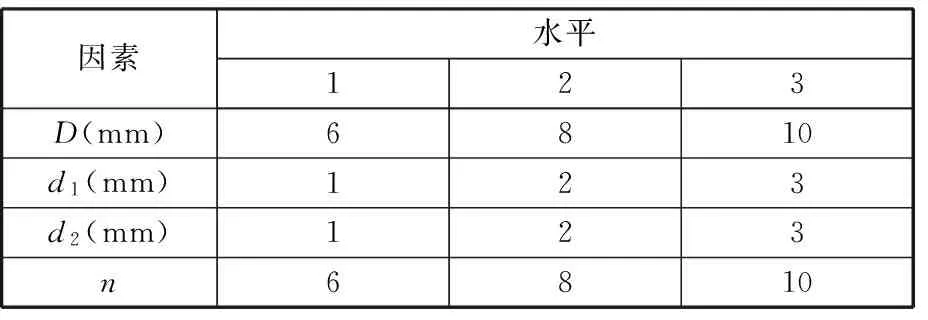
表1 隔振器正交試驗設計的因素與水平

按表2對隔振器進行有限元分析，計算固有頻率和模態損耗因子。相機隔振系統中能量主要沿相機的軸向(即隔振器的縱向)傳遞，因此主要分析隔振器的縱向一階固有頻率和模態損耗因子，橫向隔振性能最后在相機隔振系統中進行驗證。縱向一階固有頻率和模態損耗因子計算結果見表3。

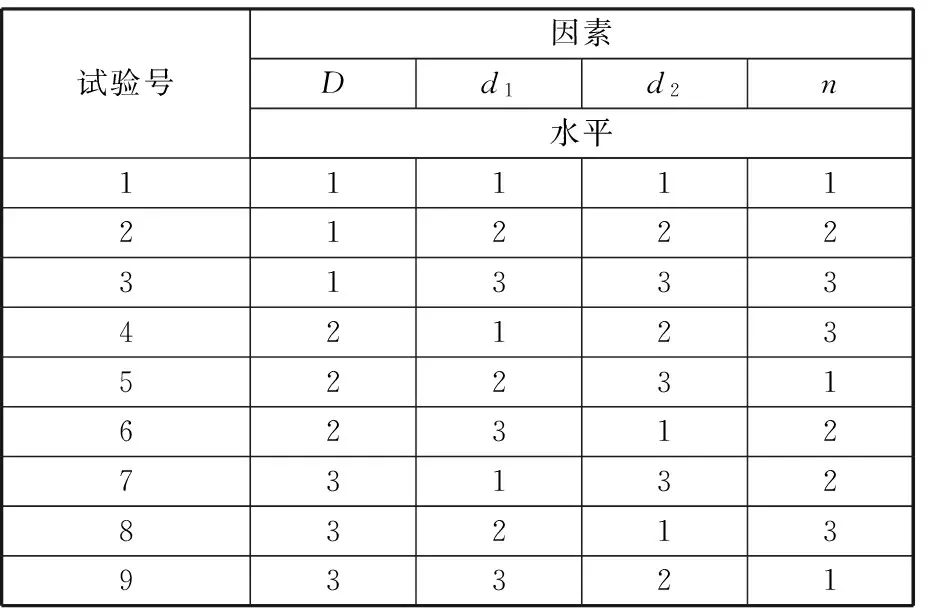
表2 隔振器正交試驗設計的L9(34)正交表

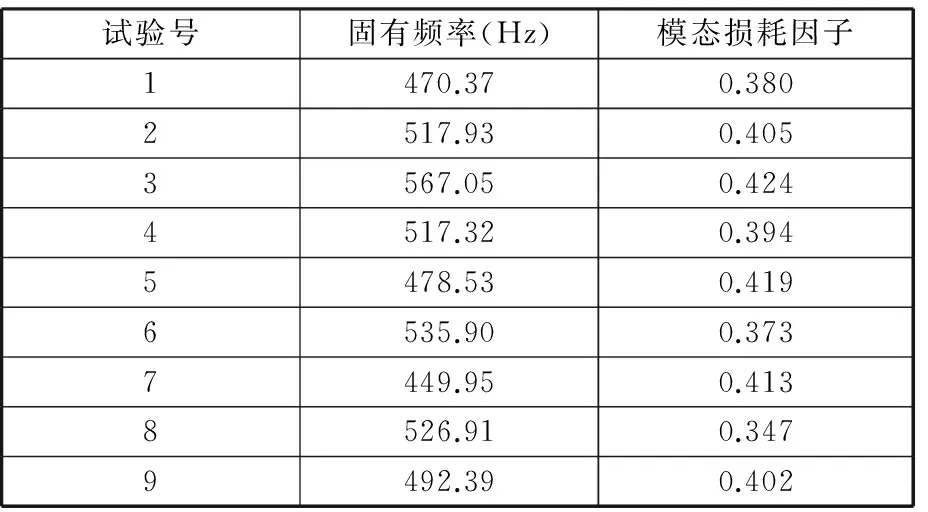
表3 隔振器正交試驗設計的計算結果

對固有頻率和模態損耗因子計算結果進行直觀分析，計算極差大小，極差大的為主要因素，極差小的為次要因素。固有頻率的直觀分析計算數據見表4。表4中,Tij表示正交表中第j列中水平i對應的試驗結果之和，i=1,2,3；Mij=Tij/3；極差Rj=max(Mij)-min(Mij)。進一步繪制因素-固有頻率圖來刻畫各個因素對固有頻率影響的趨勢和大小，如圖8所示。

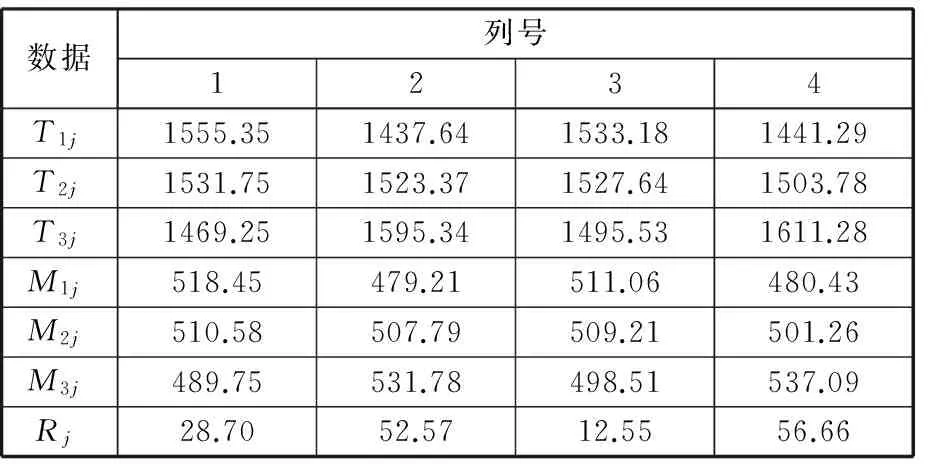
表4 固有頻率直觀分析數據

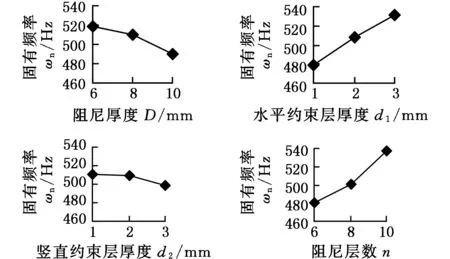
圖8 固有頻率隨各因素水平的變化Fig.8 Changes of natural frequencies with each factor and level

通過比較各因素引起的極差的大小可知,各因素對固有頻率貢獻大小的次序是阻尼層數、水平約束層厚度、阻尼層厚度、豎直約束層厚度。由圖8可知，固有頻率隨阻尼層厚度和豎直約束層厚度的增大而減小，隨水平約束層厚度和阻尼層數的增加而增大。

模態損耗因子的直觀分析數據見表5，繪制的因素-模態損耗因子圖見圖9。

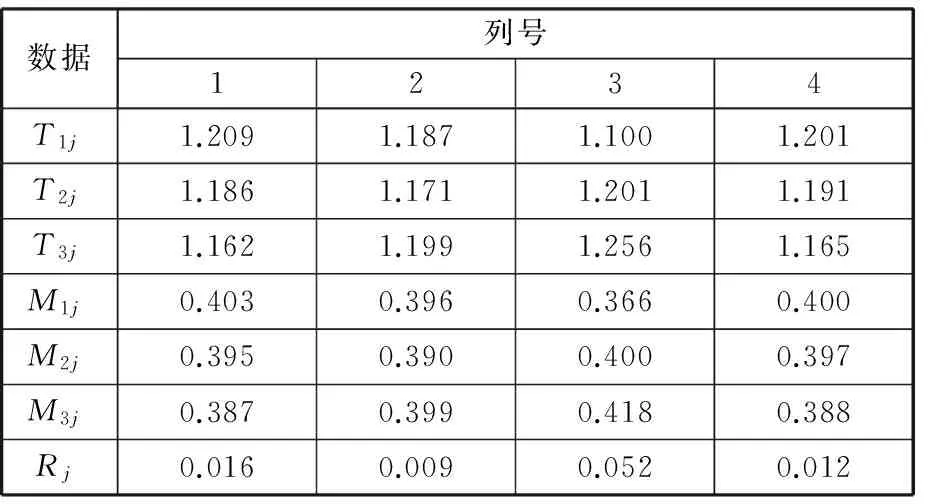
表5 模態損耗因子直觀分析數據

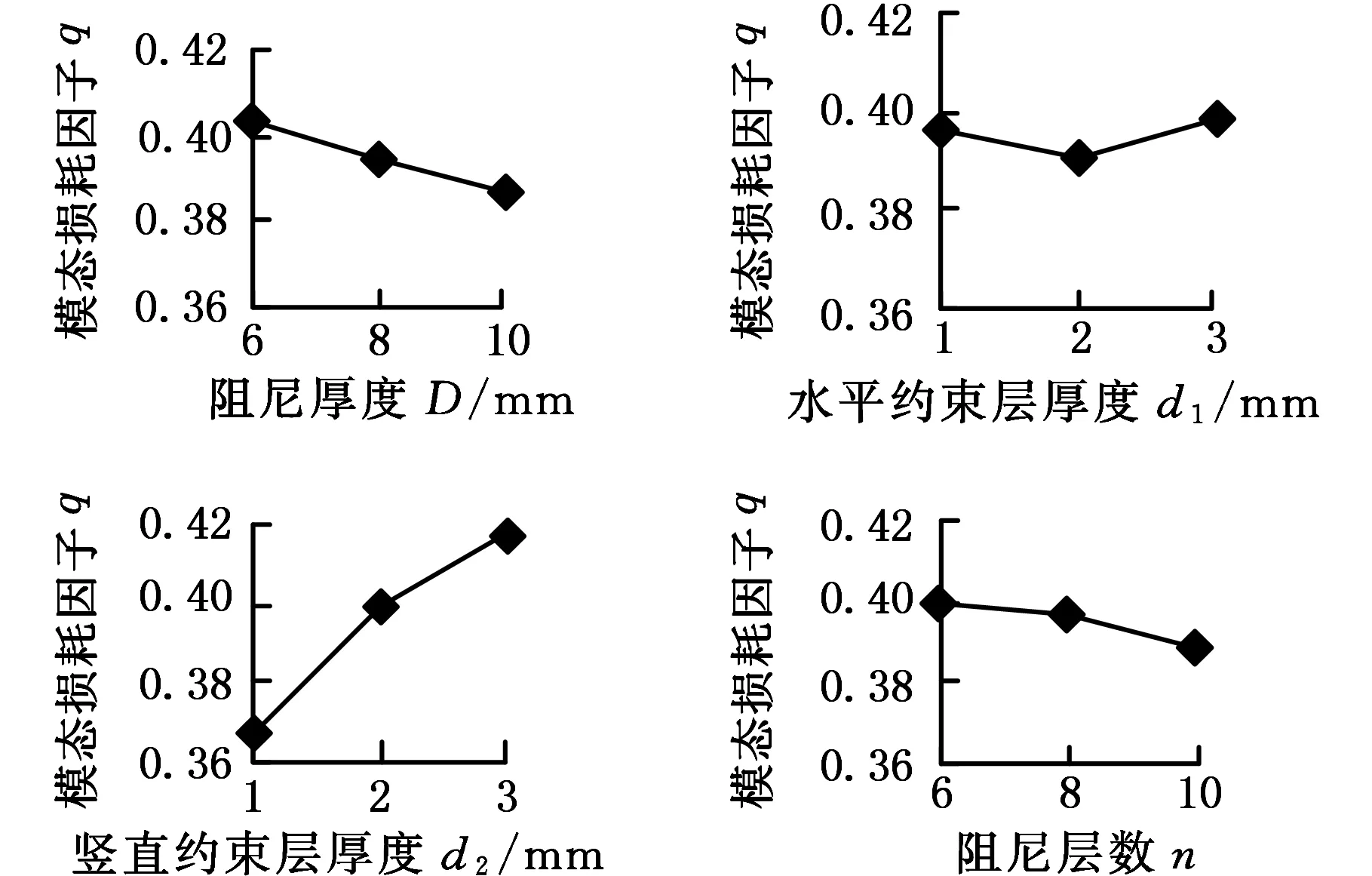
圖9 模態損耗因子隨各因素水平的變化Fig.9 Changes of modal loss factors with each factor and level

比較各因素引起的極差的大小可知,各因素對模態損耗因子貢獻大小的次序是豎直約束層厚度、阻尼層厚度、阻尼層數、水平約束層厚度。由圖9可知模態損耗因子隨水平約束層厚度的變化不是單調變化的，但幅度很小，隨阻尼層數的增加有減小趨勢，幅度也很小；隨阻尼層厚度的增大而減小，隨豎直約束層厚度的增大而有較明顯的增大。

綜合上述分析及實際結構特點，設計優化后的隔振器參數如表6所示。

定形金屬支架形式如圖10所示，隔振器的有限元模型如圖11所示。

表6 優化前后隔振器參數對比

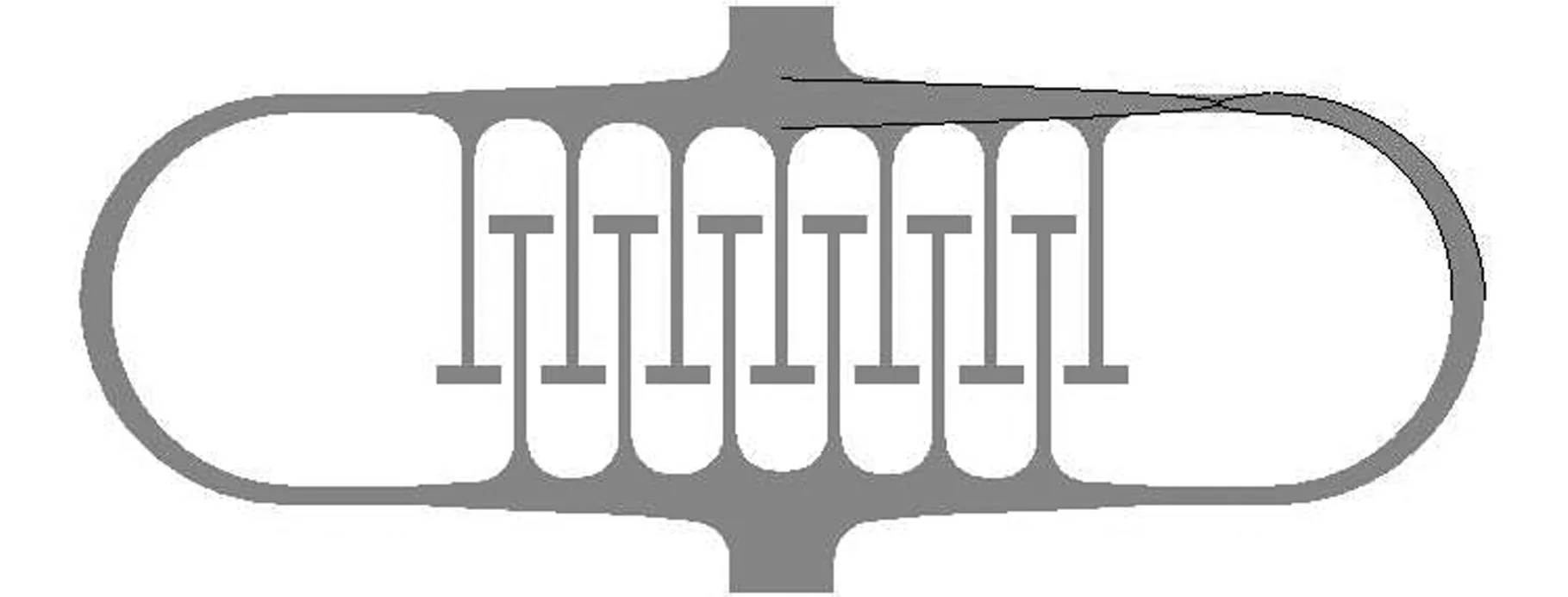
圖10 定形隔振器的金屬骨架Fig.10 Metal skeleton of the shaping isolator

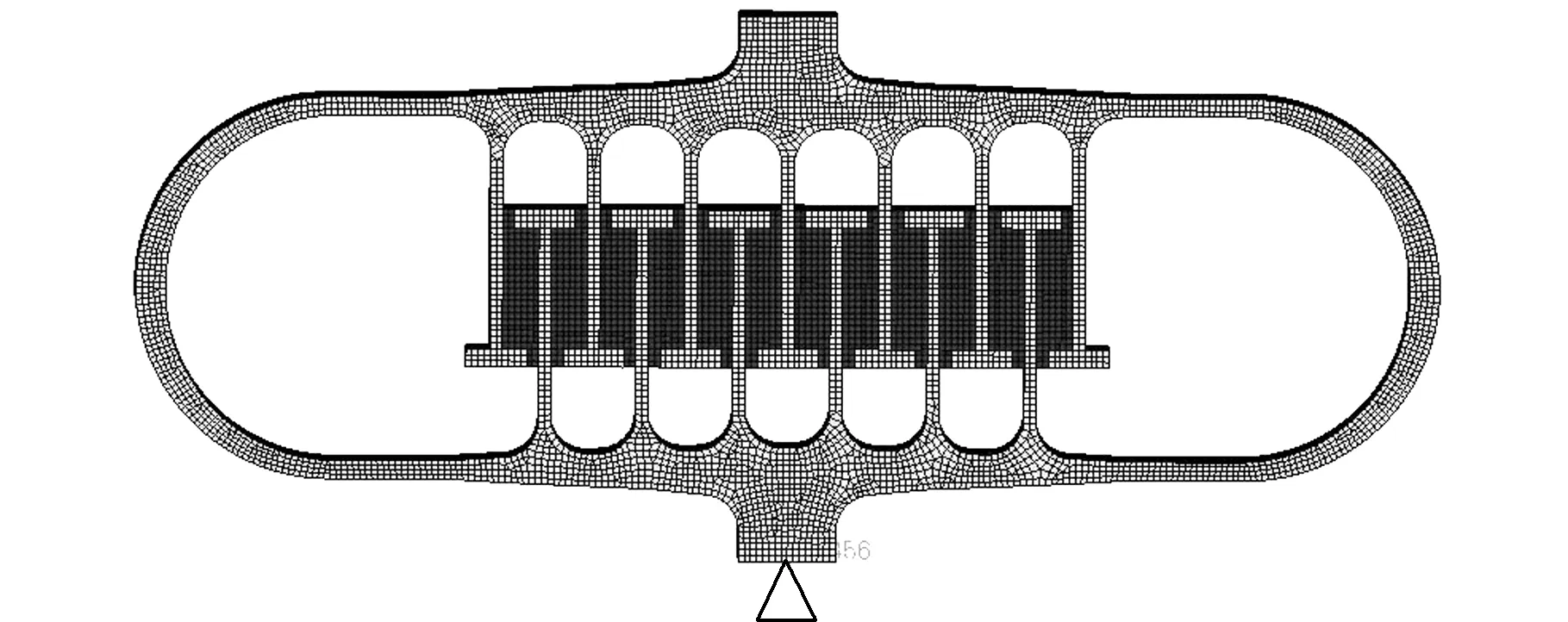
圖11 定形隔振器有限元模型Fig.11 Finite element model of the shaping isolator

對優化前后的隔振器分別進行模態計算，得到的前三階固有頻率的對比結果如表7所示，可知，優化后隔振器的前三階固有頻率都有顯著的提高。

表7 優化前后隔振器前三階固有頻率

優化前隔振器質量為0.288 kg，根據式(2)可算得縱向剛度為1.07 kN/mm；優化后質量為0.3374 kg，同樣可算得縱向剛度為4.50 kN/mm，可知優化后隔振器的縱向剛度大于2.62 kN/mm，滿足理論分析的剛度要求。由于隔振器的橫向剛度與隔振系統的橫向剛度并不滿足簡單的線性疊加關系，因而理論分析僅針對縱向剛度，后續將直接以隔振系統的橫向和縱向基頻進行驗證。

3 隔振系統的隔振性能分析

隔振系統的力學強度要求相機與隔振系統組成的組合體在軌橫向一階基頻大于18 Hz，縱向一階基頻大于35 Hz，并且能承受發射階段的考驗，不會出現材料損壞，鏡筒最大位移小于40 mm；隔振性能要求共振放大率小于4，100～150 Hz的振動傳遞率小于0.7，150 Hz以上的振動傳遞率小于0.3。

建立相機隔振系統的有限元模型，其中振動臺用大質量點模擬。對隔振器結構優化前后組成的隔振系統分別進行模態分析，優化前隔振系統的橫向(X、Y)一階基頻為12.95 Hz，縱向(Z)一階基頻為14.43 Hz，達不到基頻的要求。優化后橫向(X、Y)一階基頻提高到22.16 Hz，縱向(Z)一階基頻提高到38.03 Hz，均能滿足要求。

在系統正弦掃頻環境試驗中，隔振器受到的最大加速度載荷不應超過20g，對隔振器優化后的隔振系統進行三個方向的20g過載分析，計算出的最大位移為3.46 mm，遠小于40 mm；隔振器金屬骨架處最大應力為240.9 MPa，也遠小于鈦合金的抗拉強度890 MPa，阻尼的材料的應力僅為3.22 MPa，也在強度范圍內。可知，優化后的相機隔振系統可以滿足力學強度的要求。

在相機隔振系統有限元模型中工裝底座的大質量點處沿X、Y、Z三個方向分別輸入幅值為1，頻率范圍為0～200 Hz的簡諧加速度載荷，計算相機鏡筒上的響應，求得的頻率-加速度曲線如圖12和圖13所示。

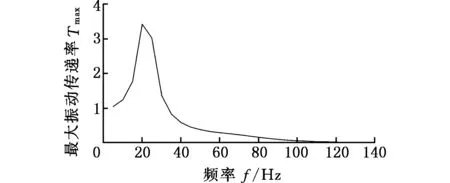
圖12 鏡筒處X、Y向的頻率-加速度曲線Fig.12 Frequency-acceleration curve of X and Y directions at the lens tube

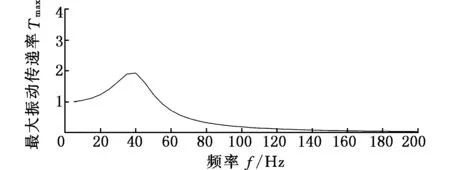
圖13 鏡筒處Z向的頻率-加速度曲線Fig.13 Frequency-acceleration curve of Z direction at the lens tube

圖12和圖13所示的頻率-加速度曲線實際上就是相機隔振系統的傳遞函數曲線，其中X、Y向的傳遞函數相同。X、Y向加速度響應最大點對應的頻率在20 Hz附近，與相機隔振系統模態分析得到的X、Y向的一階基頻基本匹配，加速度響應的幅值即共振傳遞率為3.43，100～150 Hz的最大振動傳遞率為0.061，150 Hz以上的最大振動傳遞率為0.01；Z向加速度響應最大點對應的頻率在40 Hz附近，同樣與相機隔振系統模態分析得到的Z向的一階基頻相匹配，共振傳遞率為1.93，100～150 Hz的最大振動傳遞率為0.20，150 Hz以上的最大振動傳遞率為0.083，均能滿足隔振性能的要求。

4 結論

本文從隔振理論出發，采用正交試驗設計方法，探究了實際隔振器的結構參數對其振動特性的影響，并據此對隔振器進行了結構優化設計。通過建立相機隔振系統的有限元模型來進行力學強度和隔振性能的分析，證明了隔振系統一階基頻可以滿足技術指標的要求，并且隔振系統在發射階段的20g靜力過載條件下沒有出現材料損壞和鏡筒位移過大的現象，表明隔振系統能滿足發射階段的力學強度要求；隔振系統的共振放大率及各個頻率段的振動傳遞率也均滿足要求，表明隔振系統也能滿足隔振性能的要求。由此，本文最終定形的相機隔振器可以用于衛星相機發射階段的振動隔離，并能保證較好的隔振效果。

[1] JOHNSON C D, DAVIS L P. Need for and Benefits of Launch Vibration Isolation[J]. Smart Structures and Materials: Passive Damping and Isolation,1997,3045:14-19.

[2] WINTHROP M F, COBB R G. Survey of State-of-the-art Vibration Isolation Research and Technology for Space Applications[J]. Smart Structures and Materials: Damping and Isolation,2003,5052:13-26.

[3] 馬興瑞，于登云，韓增堯，等. 星箭力學環境分析與試驗技術研究[J]. 宇航學報，2006,27(3)：323-331. MA Xingrui, YU Dengyun, HAN Zengyao, et al. ResearchEvolution on the Satellite-rocket Mechanical Environment Analysis and Test Technology[J]. Journal of Astronautics,2006,27(3):323-331.

[4] DENOYER K K，JOHNSON C D. Recent Achievements in Vibration Isolation Systems for Space Launch and On-orbit Applications[C]// 52nd International Astronautical Congress. Paris: IAF,2001:4-11.

[5] 張軍，諶勇，張志誼，等. 一種整星隔振器的研制[J]. 振動與沖擊，2005,24(5):35-38. ZHANG Jun, CHEN Yong, ZHANG Zhiyi, et al. Design and Research of a New Type of Whole-spacecraft Isolator[J]. Journal of Vibration and Shock, 2005,24(5):35-38.

[6] 張針粒，李世其，朱文革，等. 新型近等強度高阻尼航天載荷隔振器研究[J]. 振動與沖擊，2012,31(11)：1-6. ZHANG Zhenli, LI Shiqi, ZHU Wenge, et al. New Quasi-equal Strength and High Damping Isolator for Spacecraft Payload[J]. Journal of Vibration and Shock,2012,31(11):1-6.

[7] 朱石堅，樓京俊，何其偉，等. 振動理論與隔振技術[M]. 北京：國防工業出版社，2008. ZHU Shijian, LOU Jingjun, HE Qiwei, et al. Vibration Theory and Vibration Isolation[M]. Beijing: National Defense Industry Press,2008.

[8] PARKER P A, DELOACH R. Structural Optimization of a Force Balance Using a Computional Experiment Design[R]. Reno, Nevada: AIAA,2002.

[9] 方開泰，馬長興. 正交與均勻試驗設計[M]. 北京：科學出版社，2001. FANG Kaitai, MA Changxing. Orthogonal and Un-iform Experimental Design[M]. Beijing: Science Press,2001.

(編輯 袁興玲)

Structure Optimization and Isolating Performance Analysis of Spaceborne Camera Isolator

LIU Shiping1XIONG Qi1LI Shiqi1WANG Yue2

1.School of Mechanical Science and Engineering, Huazhong University of Science & Technology, Wuhan, 430074 2.Beijing Institute of Space Mechanics & Electricity, Beijing, 100076

Based on the principles of large damping loss of viscoelastic material under the action of shear forces, a spaceborne camera isolator was preliminarily designed. By using the orthogonal experimental design method and finite element analysis, the influences of the structural parameters of the isolator on the natural frequencies and modal loss factors were explored in detail, the structure of the isolator was optimized accordingly. The finite element model of the camera vibration isolation system was established, the mechanics strength was checked and the vibration isolation performances were analyzed. The results show that the camera vibration isolation system may meet the mechanics environmental tests of the satellite launching stage by using the isolators, and have better vibration isolation effectiveness.

isolator; orthogonal experimental design; structure optimization; vibration isolation system

2016-08-30

TH113.1

10.3969/j.issn.1004-132X.2017.13.002

劉世平，男，1971年生。華中科技大學機械科學與工程學院副教授。主要研究方向為智能機械及仿真、機器人遙操作。發表論文10余篇。熊 琦，男，1990年生。華中科技大學機械科學與工程學院碩士研究生。E-mail:xiongqi2016@163.com。李世其，男，1965年生。華中科技大學機械科學與工程學院教授。王 躍，男，1985年生。北京空間機電研究所高級工程師。