例談“數學核心素養”的培養

康文龍++李雪于

摘要：數學核心素養是指學生在接受相應學段的教育過程中，逐步形成的適應個人終身發展和社會發展需要的數學思維品質與關鍵能力，主要包括六個方面：數學抽象，邏輯推理，數學建模，直觀想象，數學運算，數據分析。隨著新課標的提出，素質教育被放在越來越重要的地位上，那如何在數學教學中來實現數學素養教育呢？教師在數學課堂教學中要聯系實際創造條件，大膽放手，鼓勵學生廣泛參與各種探索活動，促進個性發展，提高學生運用知識解決實際問題的能力，讓學生在實踐探索活動中加深對數學知識的理解，感受到數學學習的樂趣和應用價值所在，真正提高學生的數學素養。以下是“用二分法求方程的近似解”一堂課的教學處理，拋磚引玉，共同來探討課堂教學中的數學核心素養的培養。

關鍵詞：素質教育；數學核心素養

中圖分類號：G633文獻標識碼：A 文章編號：1992-7711（2017）13-074-1

一、提高數學直觀想象的能力

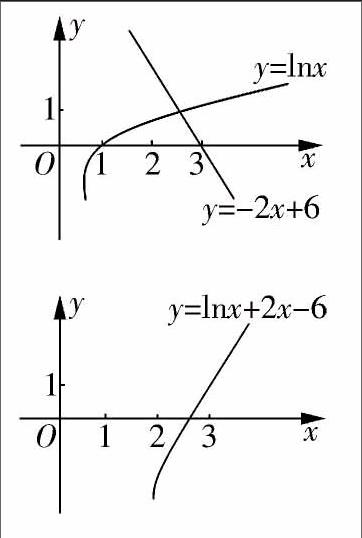
例1：求方程lnx+2x-6=0的近似解所在大致區間。

方法一：令y=lnx與y=-2x+6，方程的根就是兩個函數y=lnx與y=-2x+6圖象交點的橫坐標。接著教師用幾何畫板演示兩個函數圖象交點如圖，易得它們圖象交點的橫坐標x0∈（2，3），這樣處理使問題淺顯易懂，讓學生欣然接受。

方法二：（讓學生聯想）研究二次方程的根往往利用二次函數圖象，從而令f（x）=lnx+2x-6，可以分析出函數y=f（x）是增函數，然后用描點法畫y=f（x）圖象，可直觀得到x0∈（2，3）。最后教師用幾何畫板演示y=f（x）圖象，進行論證。

評注：數學直觀想象能力，常常的數形結合，教師可以通過直接作圖或者是利用數學教學軟件來畫圖，建立可視的效果，幫助學生直觀感受。

二、提高數學抽象的能力

例2：用二分法求方程lnx+2x-6=0的近似解。

我設置了一個引入二分法的游戲：模仿央視幸運52節目猜某一件商品價格，并使用VB程序顯示高低結果，提高學生興趣，調動學生參與積極性。

請學生猜一猜圖中導航儀的價格，已知價格處于400～800之間，給出5次機會，看誰能接近準確價格。

學生方案1：600？（高了）580？（高了）528？（低了）550？（低了）最終得出568。

（隨機猜，帶有偶然性，但400～800有太多的隨機性）

學生方案2：500？（低了）600？（高了）520？（低了）540？（低了）最終得出560。

（先每隔100猜，在100以內再每隔20猜）

學生方案3：600？（高了）500？（低了）550？（低了）575？（高了）最終得出562.5。

（每次取中點猜）

教師公布準確價格：563元，顯然方案3更好，說明二分法是解決上述問題的一種便捷的方法，接著老師開始介紹二分法原理和解題的具體過程。

評注：課堂中增加游戲環節，激發學生的求知欲，通過問題的形象化處理，提高學生的數學抽象能力。

三、提高學生的建模能力

在二分法求方程的近似解的時候，我們通過特殊結論得出一般的求法，即在區間（a，b）中如何來解決，從而提高學生的數學建模能力，算法思想主要在高中數學必修3的第一章《算法》中涉入更多，尤其是我們剛學的二分法求方程的近似解，計算量比較大，非常適合計算機處理，因此我們學好了二分法的思想方法后，學完算法，就可以利用計算機編程序，交給計算機來計算。

例如：注：以下初始區間用（a，b）表示，精確度用d表示。

最后演示程序運行結果，讓學生體會使用計算機的便捷，隨著信息技術在日新月異的發展，傳統的數學課堂已經無法滿足學生的需求，我們的課堂教學應該順應潮流，努力讓信息技術與數學課堂完美結合，使得數學課堂更有新鮮感，更具形象化，讓更多的學生來參與積極學習，從而使得課堂更加有效。

數學核心素養的培養不是一句口號，而應該正真去落實，在課堂教學中教師要讓學生在親身體驗中認識數學，解決問題，理解和掌握基本的數學知識、技能和方法；讓學生在合作交流的、獨立思考的氛圍中，傾聽、質疑、發展、提高引導學生主動參與教學全過程，主動地去創造性學習，教師要通過各種手段去培養他們的數學核心素養，正真實施素質教育。