數學學科學習力的要素及模型構建

【摘 要】 人才發展模式的變革等背景，都彰顯了培養學生學習力的迫切性.學習力的具體價值主要包括能夠改進學生的學習行為和構建基于學生學習的教學方式等.學習力可以理解為學生的生長力，對它可構建三層次六要素結構模型.數學學科學習力由一般學習力和數學學科特有的學習力（由數學學習能力、數學能力和數學創新能力等成分組成）兩部分組成.

【關鍵詞】 學習力；數學學科；要素；模型

1 背景

在信息社會的全球背景下，學習者的學習需求也正在不斷豐富，然而現代公民是否具備足夠的素質來適應瞬息萬變的社會發展呢？這就對我們教育者提出了新的要求，即如何在學校學科教育中提升學生的學習力.對學習力的思考主要基于以下幾方面的需要.

1.1 人才發展模式的變革

進入21世紀，隨著科學技術的快速發展、信息社會的沖擊、以及經濟全球化的影響，知識的表征形式與獲得方法經歷了巨大變革，尤其是終身學習機制的建立與學習型社會的構建，對學生擁有更出色的學習能力提出了更高要求.20世紀90年代開始，歐洲就尤其重視終身學習政策的規劃與實施，歐盟于1995年發表了題為《Teaching and Learning∶Towards the learning society（教與學：邁向學習型社會）》的白皮書[1]，號召歐盟各成員能對教育與學習產生新的認識與做法，通過共同努力使歐洲成為真正的學習型社會[2].報告中確立的“技能、能力與態度”指標中明確提出了五項內容，分別為識字、算數、學習型社會中所需要的新技能、學會學習的能力、積極的公民身份以及文化與社會能力[3].現在注重“基礎知識與基本技能”的教學已不能滿足培養未來的學習者.不僅學習者應明智地從學會知識轉向學會學習，我們的教育更應該注重教會學生如何學習，提升學生的學習力，以適應社會不斷發展的需求[4].

1.2 傳統教與學的困境

數學作為一門抽象、難懂的學科并不為多數學生所歡迎，但是數學學科在中小學、乃至高等教育階段都占有舉足輕重的地位.數學學科的教學質量、學生的學習方式與質量的評價已經成為當前國際教育研究和實踐的重要領域[5].依據2007年國際數學和科學評測趨勢TIMSS（The Trends in International Mathematics and Science Study）數據庫資料顯示，東亞地區學生數學學習態度遠低于世界水平，但數學成績卻高于世界平均水平，其中有高達58%的學生認為數學枯燥、不喜歡學數學[6].學生把學習數學作為任務完成，自主意愿與情感態度處于低下水平；數學教學多以高分為導向，忽視對學生學習態度、學習方式的培養.數學教與學面臨著嚴峻的挑戰，數學教學不再僅僅是知識的傳遞，更應該教會學生如何學習數學.

1.3 新課程改革的迫切要求

新課程依據時代發展及未來社會對人才的要求，提出了“適應終身學習和終身發展的基礎知識、基本技能和方法”，不僅豐富了知識的內涵，而且要求引導學生學會學習、合作、生存等，培養學生終身學習的意愿與能力.《普通高中數學課程標準（實驗稿）》中提出高中數學課程應為學生的終生發展，形成科學的世界觀、價值觀奠定基礎，對提高全民族素質具有重要作用[7].《義務教育數學課程標準（2011版）》中明確提出課程的基本理念是“使學生在充滿教學民主的過程中，提高主動學習和發展的能力”；課程目標是“培養為未來生活而自主學習、選擇和探索的能力”等等[8].與此同時，新課程更具體到教師、學生、教材、課堂等細節部分，期望通過教師角色的轉變、教學模式的變革，培養具有豐富創造力、較強學習力的現代公民.由此，用學習力的理論來指導數學新課程的教學實踐是十分必要和迫切的.

2 研究的價值

人才發展模式的變革、傳統教與學的困境以及新課程改革的迫切要求，都彰顯了培養學生學習力的迫切性.培養學生學習力，則首先需要對學習力有系統的認識，需要知曉學習力的具體價值.學習力的價值主要表現在以下三方面.

2.1 促進學生的發展

我國的教育教學改革不僅為了教師專業發展以及學生學業發展的需求，更是為了培養適應社會所需的人才.學習力的培養在此具有重大的意義，學習者通過學習將知識、過程以及情感等轉化為潛藏于自身的能量，然后在不同情境中轉化成不同形式的實踐，如解決新的問題、適應新的環境等[9].隨著學習者學習力的不斷提升，這些潛在的能量將潛移默化地促進其學習品質的不斷提高，精神素養的不斷豐富，人格的不斷健全.

2.2 改進學生的學習行為

學習動機是激發和維持學生學習行為朝向某一目標進行的內在動力，對個體的學習具有推動、引導和調節的功能[10].應試教育下培養的大批學生對數學興趣低下，多數學生為了家長的期望、升學的壓力才硬著頭皮學習數學.這些來自外源的“刺激”雖然在某種程度上也能促進學生學業成績的提高，這也就是在多次國際測評中我國學生都顯示出較高的“數學及科學素養”，然而這種學習行為僅僅是將學習活動當做獲取外在回報的一種手段；若這些外界“刺激”一旦撤離，學生則失去了學習的動力[11].數學學習力的提升有助于在一定程度上改變這一現象，尤其是學生學習行為的改進，同時改變學生的學習態度、學習意識和學習習慣等品質，使學生對數學學習充滿興趣，進而愿意學習、探索，喜歡數學.

2.3 構建基于學生學習的教學方式

教學方式是教師和學生為了實現共同的教學目標，完成共同的教學任務，在教學過程中運用方式與手段的總稱，也是有效教學的關鍵之一.課堂教學中基于學生學習行為的改變，我們的教學方式也應隨之發生變化，也即以學定教.比如在常規課堂教學中引領學生進行知識探究；加強直觀教學，注重創設情境，激發學生積極參與；創造成功機會，讓學生體驗成功感，激發學生興趣等.數學學習力要素與模型的研究能為教師教學方式的改進提供具有參考價值的信息.

3 學習力及其層次與要素

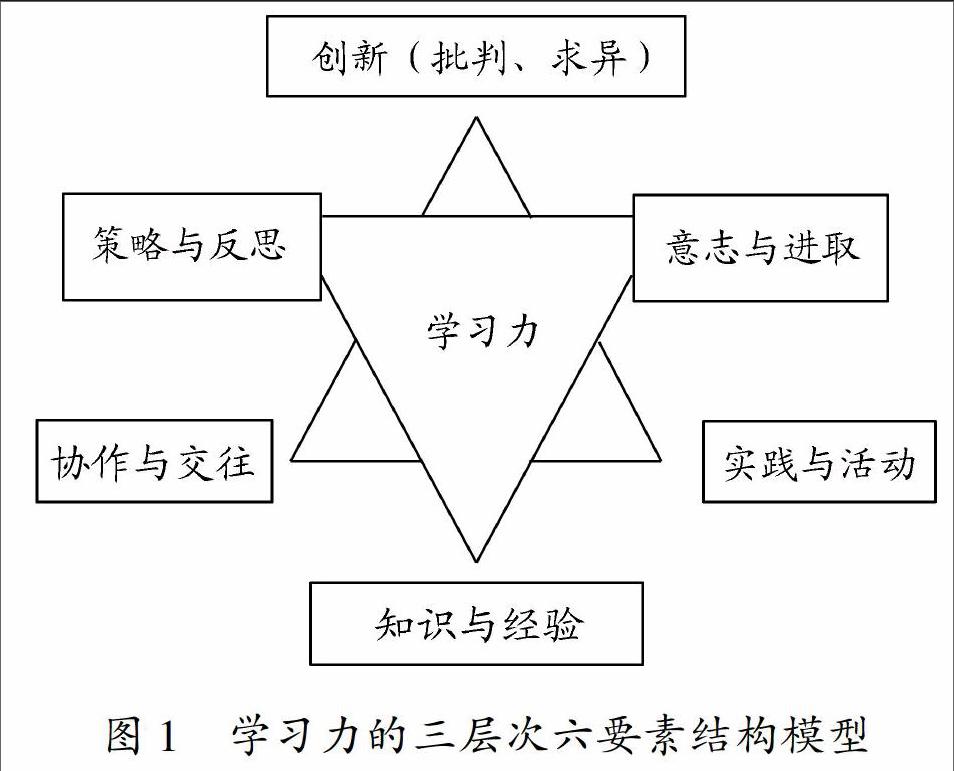
“學習力”一詞最早來源于管理學領域，多以“組織學習力”、“學習型組織”出現，它反映了組織作為一個整體對各種內外信息的認知與反應的能力[12].以學習力、學習能力、learning power、learning ability、learning capacity等為關鍵詞搜索文獻后發現，對學習力理論的系統研究主要以國外文獻為主，尤其英國相關較為突出；而國內文獻較少，目前還沒有形成系統研究.學術界普遍認為學習力是一種綜合的、復雜的能力，研究主要圍繞概念、內涵、構成要素、應用（提升策略等）進行.裴娣娜教授及其研究團隊分析、提取出學習力六大要素，它們分別是：知識與經驗、策略與反思、意志與進取、實踐與活動、協作與交往、批判與創新；并提出了學習力的三層次六要素結構模型（如圖1所示）[13].這些成果為討論學科學習力提供了借鑒與啟示.

圖1 學習力的三層次六要素結構模型4 數學學習力模型的構建

數學研究的對象是數量關系和空間形式，數學的運作在于“思維”，人腦對數學對象的思考是思維運作.數學可以理解為一種思維活動（數學活動），也可表示為這種活動的結果——理論.數學的研究對象并非物質世界中的真實存在，而是抽象思維的產物.數學與中文、英語等一樣，可被看成一種語言——科學的語言，為自然科學的研究提供了必要的概念工具.數學學習，也可以看作是學習使用這種科學語言，進入了數學的文化，養成一定的思維方式與行為方式.數學教學是數學思維活動的學與教[14].數學教學的關鍵之一是處理好理解與記憶之間的關系，特別是，理解應當被看成熟練掌握各種算法的一個必要前提.

4.1 數學學科學習力的要素和結構框架

從數學學習和數學教學的本質中可以看出，數學學科學習力的核心是思維、數學思維，提升學習力，就是促進學生數學思維的發展.而數學學科學習力由一般學習力和數學學科特有的學習力兩部分組成，其中數學學科特有的學習力又由數學能力、數學學習能力和數學創新能力等成分組成.數學學科特有的三種學習力之間的關系是：數學能力是目標，數學學習能力是為了獲得數學能力（也是促進數學學習的核心要素），數學創新能力則是進一步的發展和提升.具體結構詳見下圖2.裴娣娜教授在《變革性實踐與中國基礎教育的未來發展》[15]一書第389頁收錄了該結構圖.

4.2 數學能力的五組成分

數學能力包含很多內容，在數學學科課程中，需要重點培養學生抽象與概括、運算與推理、作圖與想象、統計與分析、建模與解釋等五組能力（學科核心素養）.

（1）抽象與概括

抽象是把同類事物或現象的共同本質屬性找出來，并舍棄其非本質屬性的思維方法.抽象的過程可以概括為分離——提純——簡略.概括是從認識個別事物的特殊本質到認識同類事物的共同特征的一種思維方法.概括要以抽象為基礎，是抽象的發展，抽象的層次越高，概括的范圍越大.林崇德先生認為：概括是形成概念的前提，是發展思維品質的關鍵[16].

例如一元二次方程模式是對許多具體的一元二次方程進行“分離—提純—簡略”，抽象其共性和本質的特點而形成的數學對象；而多項式則是對許多特殊的二次項、三次項等多項式進行更廣泛、更高層次的概括.

（2）運算與推理

計算與證明，是數學的兩個方面.所謂運算，是在運算律指導下對具體式子進行變形的演繹過程；推理是從一個或幾個判斷中得出一個新判斷的思維形式[17].推理有演繹推理、歸納推理、類比推理等.

而推理與概念、判斷一起組成邏輯思維的三個要素，數學思維還包括形象思維（空間想象）與直覺思維.事實上，一般認為，邏輯思維能力、空間想象能力和計算能力組成三大數學能力.邏輯思維能力就是正確、合理地進行思考的能力.

（3）作圖與想象

數與形是數學的兩翼.數學中的作圖能力，可按作圖過程分為兩種能力，分別是識圖能力和畫圖能力.數學中的想象能力，也就是空間想象力，是人們對客觀事物的空間形式進行觀察、分析和抽象思維的能力.

作圖能力中的識圖能力是指觀察、研究所給圖形中幾何元素之間的相互關系的能力；作圖能力中的畫圖能力又分為兩個層次，第一層次是將文字語言和符號語言轉化為圖形語言的能力，第二層次是指對圖形添加輔助圖形或對圖形進行各種變換的能力.

空間想象力主要包括下面四個方面的要求：（1）對基本的幾何圖形（平面與立體）必須非常熟悉，能正確畫圖，能在頭腦中分析基本圖形的基本元素之間的度量關系及位置關系；（2）能借助圖形來反映并思考客觀事物的空間形狀及位置關系；（3）能借助圖形來反映并思考用語言或式子所表達的空間形狀及位置關系；（4）熟練的識圖能力，即從復雜的圖形中能區分出基本圖形，能分析其中的基本圖形和基本元素之間的基本關系.

（4）統計與分析

現代社會需要人具備統計與數據分析的能力.統計能力，就是利用已具備的智力、知識、技能和非智力等要素完成統計任務的能力.數據分析能力，就是把文字或數字材料整理成格式標準的數據，并對數據進行分析，從紛繁復雜的數據中發掘出可用知識（或驗證已有知識）的能力.比如，在某一次學科測試后，學生拿到自己的成績，如果想知曉自己的成績是否進步，一個比較簡單的方法就是統計身邊幾位同學的成績，從中分析自己所處的位置，進而相對確切地判斷自己是否進步.

（5）建模與解釋

數學建模能力是在面對某個綜合性情景下，能夠理解并建構現實情境模型，會將該模型翻譯為數學問題，建立數學模型，然后會用數學方法解決該數學問題.數學解釋能力是能夠根據具體的情境，解讀與檢驗數學解答，并驗證數學模型的合理性.

數學是模式的科學.用數學的眼光看世界，產生問題，然后通過“尋模、識模、用模型”或“建模、解模、用模”，而形成新的知識結構.其中“識模、建模、解模、用模”的過程，依靠數學思維.同時解釋模型和解釋數學知識，涉及到向自己解釋，是一個理解、內化的過程；涉及到向他人解釋，是一個表達、交流的過程.

4.3 數學學習能力的五組成分

數學學習能力主要包括經驗與舊知、問題與活動、思想與方法、觀念與態度、調控與反思等五組內容.其中，（1）經驗與舊知是基礎和起點，這是學習的準備，學生并非一張白紙進入課堂.（2）問題與活動能夠驅動學生學習，問題是數學的心臟，是學生學習的起始和載體，活動是學生發現問題和解決問題的具體途徑.問題包括質疑和批判，能夠引發獨立思考，合作與交流；活動包括動手操作，動眼、動手、動口、動腦，也包括習題演練，學數學就是做數學，數學活動除了外顯的活動，更多的是內在的思維活動.（3）思想與方法需要在掌握核心概念的基礎上掌握核心思想，體驗、感悟數學思想方法.（4）觀念與態度中，觀念包括數學觀和數學學習觀，態度主要涉及非智力因素，非智力因素包括：動機、興趣、信念、意志等.（5）調控與反思則是學生的元認知（反思、歸因、監控等）過程，是學習的有效保證.

4.4 數學創新能力的三組成分

上文五組數學能力中，貫穿一條主線：實踐與創新.而這正好呼應了《國家中長期教育改革和發展規劃綱要（2010-2012）》中所提的“著力提高學生的學習能力、實踐能力、創新能力”.實踐與創新，意味著讓學生在自主學習中培養學生的創新.

數學創新能力有其核心成分，從認知過程來看，主要表現為克服思維定勢，打破常規做法；從認知結果來看，主要表現為豐富的、相異的、原創的思維產物，主要涉及數學創造力、創造能力和創新能力等.數學創新具體表現在：方法的多樣化，對比、批判、優化；對已有結論的質疑；在已解決問題的基礎上提出新的問題.

在此基礎上，我們提出數學創新能力的成分有質疑與批判、推廣與引申、聯系與貫通等.

（1）質疑與批判，能對已有數學概念、公式、公理等提出合理質疑甚至批判，質疑甚至批判不一定就能創新，但確是創新的必由之路.知識本身并不是最重要的，通過數學教學，讓學生追問數學上的為什么，養成科學的思維習慣才是最重要的.

（2）推廣與引申，能找出一些特殊問題中所蘊含的事物發展的規律，從而得到更廣泛的新結論.這種教學設計無疑增強了學生探求未知世界的信心和勇氣，使他們體會到成功到喜悅和創造性工作帶來的快樂.

（3）聯系與貫通，把學過的內容貫穿起來，加以融匯貫通，提煉出它的精神實質，抓住重點、線索和基本思想方法，組織整理成精煉的內容.知識都是相互聯系的，應努力尋找新舊知識的聯系.縱橫聯系豐富了理解.

比如，在解一元二次方程“x2-2x-l=O與x2-3x-l=0”時，一般會出現這種情況，或者都是公式法，或者都用配方法.但事實上這兩個非常相似的方程，第一題用配方法簡單，第二題用公式法較好.第一題用公式法易出現化簡不到位的問題，第二題用配方法則易出現計算錯誤.這其中則貫穿著以上三種能力，教學過程中應該鼓勵學生對于方程求解的方法唯一性提出質疑與批判，同時對于方程求解的多種方法也要進行聯系與貫通（配方法操作簡單，但僅相對適用于符合配方的形式，公式法則是萬能的；優先使用配方法，其次使用公式法），最后則需要對聯系與貫通后的認知進行推廣與引申（推廣到其他方程進行驗證，甚至引申到函數內容上）.

限于篇幅，本文僅簡單論述了數學學科學習力的要素，并初步構建了數學學科學習力的模型.（事實上，可以從不同的角度構建不同的模型.比如，唐恒鈞等在文[18]中也構建了一個模型.）在此基礎上，提升數學學科學習力的教學策略和基于數學學科學習力的數學課程結構等問題，筆者將另文敘述.

參考文獻

[1] COMMISSION E. Teaching And Learning： Towards The Learning Society[M]. Bruxelles∶European Co mmission press，1995.

[2] 陳學軍， 鄔志輝. 歐洲終身學習質量指標述評[J].外國教育研究， 2005， 32（7）： 45-9.

[3] COMMISSION E. European report on quality indicators of lifelong learning [J]. Brussels： European Co mmission press， 2002.

[4] 楊艷艷. 掌握學習視角下初中生學習力提升策略研究[D].南京師范大學， 2012.

[5] 孔企平. 國際數學學習測評： 聚焦數學素養的發展[J].全球教育展望， 2011， 40（11）： 78-82.

[6] 王娟. 數學學習的情感， 自信， 價值與成就之關系——由 TIMSS 2007 的結果分析亞洲五國 （地區） [J].外國中小學教育， 2009（10）： 46-9.

[7] 教育部. 普通高中數學課程標準 （實驗稿） [M]. 北京： 人民教育出版社. 2003.

[8] 教育部. 義務教育數學課程標準[M].北京： 北京師范大學出版社. 2011.

[9] 楊艷艷，陳維維. 面向學習過程的學習力提升探索[J].南京曉莊學院學報， 2012（6）：101-104.

[10] 李伯黍，燕國材.教育心理學[M].上海：華東師范大學出版社， 1993.

[11] 曹威麟，段曉群，郭江平.心理契約對高校學生學習行為的影響機制研究[J].現代大學教育， 2007（4）：105-109.

[12] A. K. Yeung，D. O. Ulrieh ， S. W. Nason and M.A. Von Glinow .Organizational Learning Capability ： Generating Ideas with Impact [M].Oxford University Press，1999.

[13] 裴娣娜. 學習力： 詮釋學生學習與發展的新視野[J].課程·教材·教法， 2016， 36（7）： 3-9.

[14] 朱哲，陸吉健.數學教學是數學思維活動的學與教[J].中學數學月刊， 2014（4）：9-11.

[15] 裴娣娜.變革性實踐與中國基礎教育的未來發展[M].北京： 教育科學出版社. 2015.

[16] 林崇德.智力發展與數學學習[M].北京： 中國輕工業出版社. 2011.

[17] 曹才翰.中學數學教學概論[M].北京： 北京師范大學出版社. 1990.

[18] 唐恒鈞，陳碧芬，張維忠. 基于學習力視角打高中數學課程建設[J].當代教育與文化， 2016， 8（2）： 17-21.