連續型隨機變量的分布函數的計算方法

王仲梅,孟獻青

(1.湖南商學院數學與統計學院，湖南長沙410000;2.山西大同大學數學與計算機科學學院，山西大同037009)

連續型隨機變量的分布函數的計算方法

王仲梅1,孟獻青2

(1.湖南商學院數學與統計學院，湖南長沙410000;2.山西大同大學數學與計算機科學學院，山西大同037009)

通過實例給出了如何用定義計算連續型隨機變量的分布函數，并且給出了另外一種相對簡單的求一維連續型隨機變量的分布函數的方法。

連續型隨機變量；分布函數；連續函數；概率密度函數

在概率統計中，對于連續型隨機變量X，若已知概率密度 f(x)，求分布函數F(x)的公式很簡單，即在用這個公式求分布函數的時候主要有兩種情況[1-3]：第一種是 f(x)是非分段函數，例如標準正態分布這時候直接利用公式可以計算出F(x)=這種情況相對比較簡單；第二種是 f(x)是分段函數，這類問題在本科學習階段比較多，而且部分學生會覺得比較難。下面我們主要討論 f(x)是分段函數的情形。

定義1設X是一個隨機變量，x∈R，則稱F(x)=P(X≤x)為隨機變量X的分布函數。

由定義1，分布函數F(x)顯然滿足：

（1）單調不減，即若 x1,x2∈R ，且 x1≤x2，則F(x1)≤F(x2)；

（2）0≤F(x)≤1，且F(-∞)=0,F(+∞)=1 ；

下面我們討論兩種求解F(x)的方法：

方法1：定義法

定義2如果對于隨機變量X的分布函數F(x)，存在非負可積函數 f(x)，對任意 x∈R有

解：根據分布函數的定義知，分布函數的定義域是R。 f(x)是個分段函數，它的分段點將數軸分成了四個區間，所以我們在每個區間上進行。

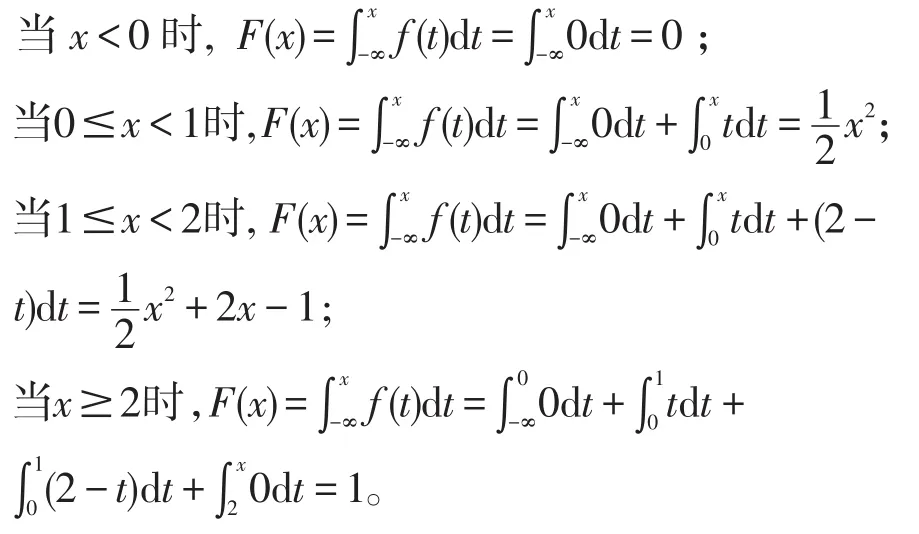
所以，隨機變量X的分布函數

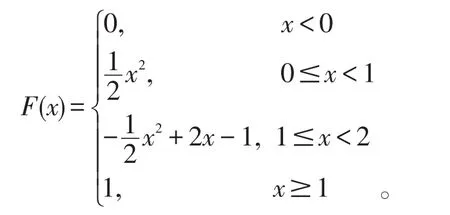
方法2：求 f(x)的一個原函數F(x)，

先給出下面兩個簡單的定理。

定理1連續型隨機變量的分布函數是連續函數。

證明由定義2知連續型隨機變量的分布函數是一個變上限函數，從而是連續函數。

定理2若連續型隨機變量X具有概率密度

證明由分布函數的性質 F(-∞)=0,F(+∞)=1知，C1=0,(x〈a1),Cn=1,(x∈其他),又因為 F(x)=所以在每個連續的區間段內F′(x)=f(x)，即F(x)是 f(x)的一個原函數，所以∫hn(x)dx=Gn(x)+Cn，又因定理1知F(x)是連續函數，所以

解：由定理2知：

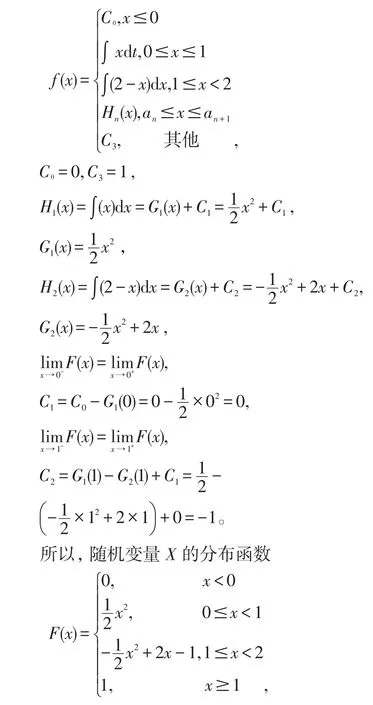
綜上，方法2與方法1相比，把方法1中求的公式中定積分計算轉化成了簡單不定積分的計算，相對簡化了計算量。

[1]韓旭里.概率論與數理統計[M].上海：復旦大學出版社,2012.

[2]熊萬年.概率論與數理統計[M].長春：東北師范大學出版社,2014.

[3]桂春燕.連續的分布函數與連續型隨機變量的關系[J].安慶師范學院學報（自然科學版），2015(2)：101-102.

The Calculation Method for Distribution Function of Continuous Random Variable

WANG Zhong-mei1,MENG Xian-qing2
（1.School of Mathematics and Statistics,Hunan Business College,Changsha Hunan,410000;2.School of Mathematics and Computer Sciences,Shanxi Datong University,Datong Shanxi,037009）

In this paper,an example shows how to compute distribution function of the continuous random variable by definition and presents an other method.Compared to the definition,the present method is simpler and costs less calculation.

continuous random variable;distribution function;continuous function;the probability density function.

O175

A

〔責任編輯 高海〕

1674-0874(2017)01-0016-02

2016-10-15

王仲梅(1980-)，女，山西大同人，碩士，講師，研究方向：圖論及其應用。