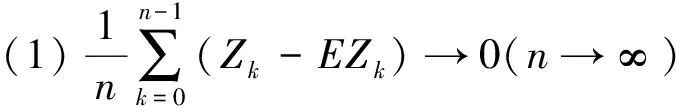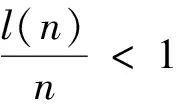多重隨機環境中馬氏鏈及其強大數定律
費時龍
(宿州學院 數學與統計學院, 安徽 宿州 234000)
多重隨機環境中馬氏鏈及其強大數定律
費時龍
(宿州學院 數學與統計學院, 安徽 宿州 234000)
引入了多重隨機環境中的馬爾科夫鏈模型,該模型是隨機環境中馬爾科夫鏈模型的推廣,適用范圍更廣.給出了多重隨機環境中馬爾科夫鏈模型的2個應用背景;討論了m重隨機環境中馬爾科夫鏈、n重隨機環境中馬爾科夫鏈、馬氏鏈、2m維鏈的相互關系及性質.最后,利用得到的多重馬氏鏈的相關性質獲得了多重隨機環境中馬爾科夫鏈強大數定律成立的充分條件,推廣了部分文獻的結論.
隨機環境;m重馬氏鏈;強大數定律
0 引 言
馬爾科夫鏈(以下簡稱經典馬氏鏈)是隨機過程中最重要的分支之一,其理論已廣泛應用于金融、保險、現代物理、分子生物學、隨機服務系統等領域.基于經典馬氏鏈理論研究,考慮到經典馬氏鏈中的轉移函數會受外部隨機因素的干擾,COGBURN[1]增加了隨機變量,并引入了隨機環境中的馬爾科夫鏈模型(簡稱MCRE).自20世紀80年代以來,MCRE的理論研究得到了各國學者的廣泛關注,并取得了豐富的成果.COGBURN在MCRE的狀態分類與性質[1-2]、中心極限定理[3]等方面獲得了豐富的研究成果.OREY[4]對COGBURN等的工作進行了總結和評價,同時得到類似于經典馬氏鏈理論方面的很多成果并提出一些問題.李應求[5-7]研究了MCRE的常返性.胡迪鶴[8-9]給出了MCRE的構造.近年來,MCRE極限理論及其研究受到很多學者的重視,王漢興等[10]研究了MCRE的Poisson極限律,方大凡[11]研究了MCRE的Shannon-McMillan-Breiman定理,郭明樂[12-13]、萬成高[14]、王偉剛[15]分別研究了MCRE的強大數定律.胡迪鶴[16]則對MCRE作了詳細介紹與研究.本文主要討論MCRE模型的推廣,通過引入多重隨機環境中的馬爾科夫鏈模型,討論m重隨機環境中的馬爾科夫鏈、k重隨機環境中的馬爾科夫鏈、MCRE、雙鏈、2m維鏈的相互關系,給出研究多重隨機環境中馬爾科夫鏈的一種方法,以獲得多重隨機環境下馬爾科夫鏈強大數定律成立的充分條件.推廣了部分文獻的結論.
1 m重MCRE模型及性質


(i)對任意θm∈Θm及xm∈Xm,p(θm;xm,·)是A上的概率測度.
(ii)對任意θm∈Θm及A∈A,p(θm;·,A)關于Am可測.
(iii)對任意xm∈Xm及A∈A,p(·;xm,A)關于Bm可測.
(iv)對任意A∈Ap(·;·,A)關于Bm×Am可測.
則稱p(·;·,·)為一個m重隨機馬爾科夫核.


(1)

(2)


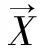
證明 設p(·;·,·)為一個m重隨機馬爾科夫核,若記
p((θn,…,θn+k-1);(xn,…,xn+k-1);A)=
p((θn+k-m,…,θn+k-1);(xn+k-m,…,xn+k-1);A),


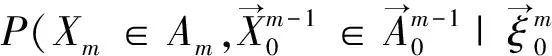
從而由單調類定理易得


注2 由注1及定理1知,m重隨機環境中的馬爾科夫鏈是隨機環境中馬爾科夫鏈模型的推廣,其直觀想法為:系統或過程未來(n+m時刻)的演變規律只與最近一段時間內(n時刻到n+m-1時刻)系統或過程所處的狀態和環境有關,與過去(n時刻之前)無關.
下面給出該模型的2個應用背景.
例1(生物群體繁殖模型) 研究某種生物群體數量的演變規律,以Xn表示第n個單位時刻生物群體的數量,ξn表示第n個單位時刻生物群體所處的外部環境,若不考慮環境因素的變化(即假定ξn為常量),且假定已知過去和現在群體數量,下一個單位時間群體數量的演變規律只與現在有關,即在X0,X1,…,Xn狀態已知的條件下,Xn+1所處狀態的轉移規律只與Xn有關,與X0,X1,…,Xn-1無關,即為經典的馬爾科夫鏈模型.更一般地,考慮生物群體受生育和存活時間段及外部環境的隨機變化影響,在過去和現在群體數量和外部環境所處狀態已知的條件下,群體數量下一個單位時間的演變規律只與現在至過去一段時間內的群體數量和環境狀態有關,即在X0,X1,…,Xn+m-1,ξ0,ξ1,…,ξn+m-1所處狀態已知的條件下,Xn+m只與Xn,Xn+1,…,Xn+m-1,ξn,ξn+1,…,ξn+m-1所處的狀態有關,該模型即為m重隨機環境中的馬爾科夫鏈.
例2(短線交易中的股票價格預測模型) 研究某種股票價格的預測模型,若換手率較高,則表明大部分投資人會在較短的時間內發生交易.將時間離散化,以Xn,n=0,1,2,…表示在n時刻股票的價格,以ξn,n=0,1,2,…表示在n時刻的外部環境(如經濟政策、公司經營狀況、市場環境等因素),在不考慮環境因素變化(即假定ξn為常量)且假定在過去和現在股票價格已知的條件下,股票價格下一個單位時間的演變規律只與現在有關,與過去無關,即在已知X0,X1,…,Xn狀態的條件下,Xn+1所處狀態的轉移規律只與Xn有關,與X0,X1,…,Xn-1無關,即為經典的馬爾科夫鏈模型.該模型的假設過于理想化,不符合股市的運行規律.一般情形下,由于短期內大部分投資人會發生交易,因此,假設在已知過去和現在股票價格和外部環境所處狀態的條件下,股票價格下一個單位時刻的演變規律只與現在至過去一段時間內的股票價格和環境狀態有關是合理的.即在已知X0,X1,…,Xn+m-1,ξ0,ξ1,…,ξn+m-1所處狀態的條件下,Xn+m只與Xn,Xn+1,…,Xn+m-1,ξn,ξn+1,…,ξn+m-1所處的狀態有關,該模型即為m重隨機環境中的馬爾科夫鏈.
定理2 下列條件等價:
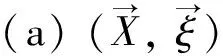
(b)下列條件成立:
(c)下列條件成立:
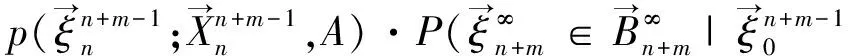
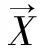
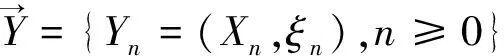
(2) {Wn=(Xn,Xn+1,…,Xn+l-1,ξn,ξn+1,…,ξn+l-1),n≥0}為馬爾科夫鏈.
P((Xn+l,ξn+l)∈A×B)|
((Xn+l-1,ξn+l-1),…,(Xn,ξn)).
(2)令Wn=(Yn,Yn+1,…,Yn+l-1),
則由(1)知{Yn=(Xn,ξn),n≥0}為一個l重馬爾科夫鏈,從而
{Wn=(Yn,Yn+1,…,Yn+l-1),n≥0}
為馬爾科夫鏈.
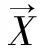
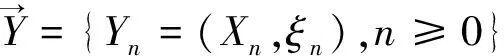
(2) 2m維鏈{Wn=(Yn,Yn+1,…,Yn+m-1),n≥0}為馬爾科夫鏈.
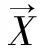
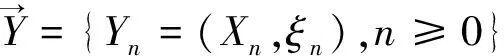
(2) 2m維鏈{Wn=(Yn,Yn+1,…,Yn+m-1),n≥0}為時齊的馬爾科夫鏈.
2 m重MCRE的強大數定律
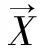
P((Yn,Yn+1,…,Yn+m-1)=
(x0,θ0,x1,θ1,…,xm-1,θm-1), i.o.)=1
(1)
成立,即(x0,θ0,x1,θ1,…,xm-1,θm-1)是Wn的一個常返狀態.對每個k≥0,τ0≡0,定義一列馬爾科夫時間為
τk+1=inf{n>τk:(Yn,Yn+1,…,Yn+m-1)=
(x0,θ0,x1,θ1,…,xm-1,θm-1)},
令
σk=τk+1-τk, Ωτk={τk<∞},
Fn=σ((Xi,ξi):0≤i≤n+m-1),
Fτk={A?Ωτk:?n≥0,A∩{τk≤n}∈Fn},
Fτk=σ((Xτk+n,ξτk+n):n≥0).
再令l(n)=k,當τk 則有 引理1 (i){Zk,k≥0}是概率空間(Ω,F,P)上的獨立隨機變量列. (ii)若EZk有限,?k≥0,則 ∫{l(n) 證明 (i)由假設知{Zk,k≥0}是取至多可列多個值的隨機變量,且對任意實數cr(0≤r {Zr=cr,τk=n}= 所以Y0,Y1,…,Yk-1是Fτk可測的,令w=(x0,θ0,x1,θ1,…,xm-1,θm-1),則 {σk=u}={Wτk+1≠w,…,Wτk+u-1≠w,Wτk+u=w}∈Fτk. 從而由強馬氏性質知 P(Z0=c0,Z1=c1,Zk-1=ck-1,Zk=ck)= P(Z0=c0,Z1=c1,Zk-1=ck-1)P(Zk=ck). 利用數學歸納法易證引理1的(i)成立. (ii){l(n) ∫{l(n) ∫l(n) ∫{l(n) 推論3 對任意實數a,b,{aZk+bσk,k≥0}與{aUk+bσk,k≥0}均為(Ω,F,P)上的獨立隨機變量列,且{σk,k≥0}為(Ω,F,P)上的獨立同分布隨機變量列. 條件I 存在非負且數學期望有限的隨機變量Y,使得對任意x>0,n∈N,有 qn(x)≡P(Un(x)+σn(x)>x)≤ q(x)≡1-FY(x). 引理2[2]若滿足條件I,則對任意n≥0,有 (1)E|Zn|+Eσn≤EUn+Eσn≤EY<∞; 引理3[17]若滿足條件I,則 引理4 若滿足條件I,則 證明 由l(n)的定義知: 顯然,上式最后一個等式第1項為0,由引理1知第2項為0,從而有 故由引理2知 引理5 若滿足條件I,則 即 定理4 若滿足條件I,則有下列強大數定律成立: 0(n→∞) a.s. 證明 顯然 由引理2~5知,上式每項均幾乎處處收斂于0,所以定理得證. 推論4 設gi(·,·)為滿足條件I的二元函數,則有下列強大數定律成立: 證明 只需在定理3中令 fi(Xi,ξi,Xi+1,ξi+1,…,Xi+m-1,ξi+m-1)=gi(Xi,ξi). 注3 推論4即為文獻[13]的主要結果. [1] COGBURN R. Markov chains in random environments[J]. Ann Probab,1980,8(3):908-916. [2] COGBURN R. The ergodic theory of Markov chains in random environments[J]. Probability Theory and Related Fields,1984,66(1):109-128. [3] COGBURN R. On the central limit theorem for Markov chains in random environments[J]. Ann Probab, 1991,19(2):587-604. [4] OREY S. Markov chains with stochastically stationary transition probabilities[J]. Ann Probab,1991,19(3):907-928. [5] 李應求.雙無限環境中馬氏鏈的常返性與不變側度[J].中國科學:A輯,2001,31(8):702-707. LI Y Q. The recurrence and invariant measures for Markov chains in bi-infinite environments[J]. Science in China:Ser A,2001,31(8):702-707. [6] 李應求.雙無限隨機環境中馬氏鏈的暫留性[J].數學物理學報:A輯,2007,27(2):269-276. LI Y Q. Transience for Markov Chains in double infinite random environments[J]. Acta Mathematica Scientia:Ser A,2007,27(2):269-276. [7] 李應求.雙無限隨機環境中的常返馬氏鏈[J].數學學報:A輯,2007,50(5):1099-1100. LI Y Q. The recurrent Markov chains in bi-infinite random environments[J]. Acta Mathematica Sinica: Ser A,2007,50(5):1099-1100. [8] 胡迪鶴.隨機環境中q-過程的存在唯一性[J].中國科學:A輯,2004,34(5):625-640. HU D H. The existence and uniqueness ofq-process Science in random environments[J]. Science in China: Ser A,2004,34(5):625-640. [9] 胡迪鶴.從P-m鏈到隨軍環境中的馬氏鏈[J].數學年刊:A輯,2004,25(1):65-78. HU D H. FromP-mchains to Markov chains in random environments[J]. Chinese Annals of Mathematics:Ser A,2004,25(1):65-78. [10] 王漢興,戴永隆.馬氏的Poisson極限律[J].數學學報,1997,40(2):266-270. WANG H X, DAI Y L. Poisson limit law for Markov a chains in Markovian environments[J]. Acta Mathematica Sinica,1997,40(2):266-270. [11] 方大凡.馬氏環境中馬氏鏈的Shannon-McMillan-Breiman定理[J].應用概率統計,2000,16(3):295-298. FANG D F. Shannon-McMillan-Breiman theorem for Markov chains in Markovian environments[J]. Chinese Journal of Applied Probability and Statistics, 2000,16(3):295-298. [12] 郭明樂.馬氏環境中的馬氏鏈的強大數定律[J].應用數學,2003,16(4):143-148. GUO M L. The strong law of large numbers for Markov chains in Markovian environments[J]. Mathematica Applicata,2003,16(4):143-148. [13] 郭明樂.隨機環境中的馬氏鏈的強大數定律[J].應用概率統計,2004,20(2):154-160. GUO M L. The strong law of large numbers for Markov chains in random environments[J]. Chinese Journal of Applied Probability and Statistics, 2004,20(2):154-160. [14] 萬成高.馬氏環境中馬氏鏈的強大數定律[J].應用概率統計,2003,19(2):155-160. WAN C G. On the strong law of large numbers for Markov chains in Markovian environments[J]. Chinese Journal of Applied Probability and Statistics, 2003,19(2):155-160. [15] 王偉剛.一般隨機環境中馬氏鏈的強大數律[J].數學雜志,2011,31(3):481-487. WANG W G. The strong law of large numbers for Markov chains in random environments[J]. Journal of Mathematics, 2011,31(3):481-487. [16] 胡迪鶴.隨機環境中的馬爾可夫過程[M].北京:高等教育出版社,2011. HU D H. Markov Processes in Random Environments[M]. Beijing: Higher Education Press,2011. [17] 朱成熹.隨機極限引論[M].天津:南開大學出版社,1987. ZHU C X. An Introduction to Random Limit[M]. Tianjin: Nankai University Press, 1987. The multiple Markov chains in a random environment and the strong law of large numbers. FEI Shilong (SchoolofMathematicsandStatistics,SuzhouUniversity,Suzhou234000,AnhuiProvince,China) The model of multiple Markov chains in a random environment is introduced which is a promotion of Markov chains in a random environment with a more general application scope. Two application backgrounds of the multiple Markov chains in a random environment are given. Then, we discuss some relations and properties of the ordermMarkov chains and the orderkMarkov chains in a random environment,Markov chains, and 2mdimensional chains. At last, using the property of the multiple Markov chains in a random environment, we obtain the sufficient condition of the strong law of large numbers of the multiple Markov chains in a random environment, which are a promotion of the results from some literatures. random environments; Markov chains with orderm; strong law of large numbers 2016-01-18. 安徽省高等學校省級自然科學基金資助項目(KJ2016A770);安徽省高校優秀青年人才支持計劃重點項目(gxyqZD2016340). 費時龍(1980-),ORCID:http://orcid.org/0000-0003-4352-9345,男,碩士,副教授,主要從事隨機過程研究,E-mail:fsl627@sina.com. 10.3785/j.issn.1008-9497.2017.04.005 O 211.62 A 1008-9497(2017)04-411-06 Journal of Zhejiang University(Science Edition), 2017,44(4):411-416