基于軟競爭Yu范數自適應共振理論的軸承故障診斷方法

慕海林 王志剛 徐增丙

自適應共振理論的軸承故障診斷武漢科技大學機械自動化學院，武漢，430081

?

基于軟競爭Yu范數自適應共振理論的軸承故障診斷方法

慕海林 王志剛 徐增丙

自適應共振理論的軸承故障診斷武漢科技大學機械自動化學院，武漢，430081

傳統自適應共振理論網絡模型利用硬競爭機制對故障類邊界處的樣本進行分類時易造成誤分類，為此，提出了基于軟競爭Yu范數自適應共振理論的軸承故障診斷方法。將基于模糊競爭學習的軟競爭方法引入Yu范數自適應共振理論模型中，根據模式節點與輸入樣本間隸屬度的大小，對競爭層多個節點進行訓練和學習。通過對軸承故障試驗數據的診斷分析可知，該方法不但能有效識別不同類型的故障，而且能識別不同嚴重程度故障，且診斷精度優于自適應共振理論模型和模糊C均值聚類模型。

故障診斷；自適應共振理論；軟競爭；Yu范數

0 引言

滾動軸承是機械系統中常用的重要部件，其運行狀態直接影響整個系統的性能，一旦發生故障或失效，將引發設備產生災難性后果，因此，對軸承故障進行診斷具有重要意義。人工神經網絡因其非線性映射、魯棒性強、自組織和自學習能力強等特點，在故障診斷中得到了廣泛的應用[1-3]。傳統神經網絡不能在保存以前學習知識的前提下接納新的模式，導致其應用范圍受到了限制。自適應共振理論(adaptive resonance theory，ART)神經網絡模型解決了傳統神經網絡“適應性”與“穩定性”兩難的問題，而廣泛應用于模式識別、故障分類等領域。但ART網絡采用硬競爭機制，浪費了神經元信息，常將處于故障類邊界處的數據點強行誤分為另一故障類，導致診斷精度不高。針對這一問題，筆者將軟競爭方法[4]引入ART網絡模型，提高神經元節點信息的利用率，從而提高診斷模型的診斷效果。

1 ART神經網絡

ART神經網絡[5]利用生物神經細胞之間自興奮與側抑制的動力學原理，讓輸入模式通過網絡的雙向連接進行識別與比較，通過達到共振狀態完成網絡的訓練與學習，解決了傳統神經網絡“適應性”與“穩定性”兩難的問題，其基本結構如圖1所示。網絡分為比較層F1和識別層F2，當一個輸入模式提交給網絡的F1層時，在F2層比較各節點與輸入模式的相似度；硬競爭機制下，F2層每次只有一個節點被激活，并在F1層對應一個反饋信號，反饋信號在F1層與輸入模式進行比較。如果輸入模式與反饋信號不能匹配，調整子系統將重置F2層，并取消當前勝出的神經元和相對應的反饋信號，從而產生新一輪的競爭。F2層新勝出的神經元通過反饋連接向F1層產生一個新的反饋信號，并在F1層再次進行比較，如此反復地調整、重置，最終達到諧振狀態，整個神經網絡在諧振狀態下不斷學習和調整，直到反饋值與輸入模式成功匹配完成學習[6]。

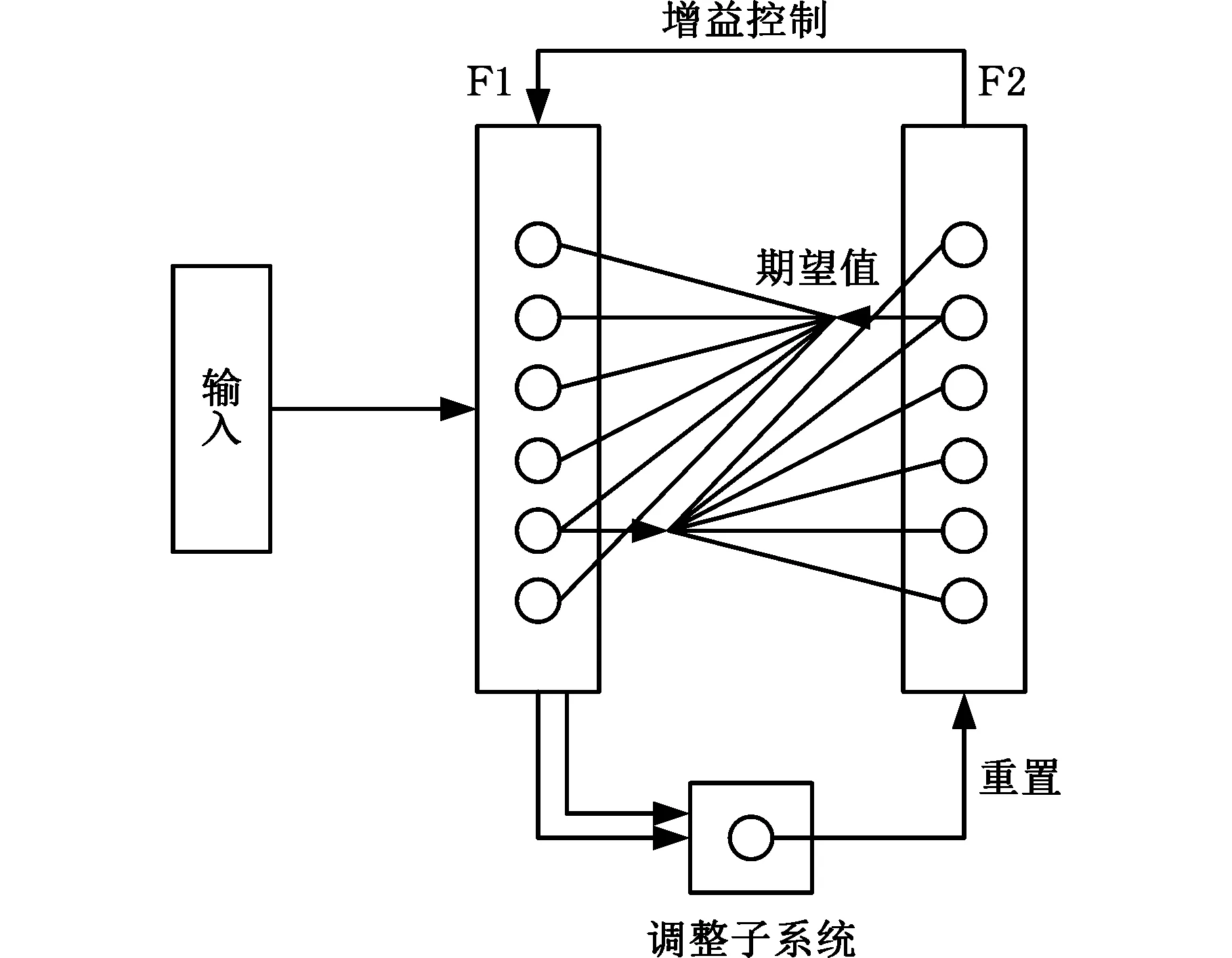
圖1 ART網絡基本結構Fig.1 Basic structure of ART

2 基于軟競爭的Yu范數ART神經網絡

2.1 基于Yu范數的ART神經網絡

Yu范數[7]由T范數和S范數組成，其數學表達式為

T(x，y)=max(0，(1+τ)(x+y-1)-τxy)

(1)

S(x，y)=min(1，x+y+τxy)

(2)

x，y∈[0，1]τ>-1

根據Yu范數的特有性質，LUUKKA[8]提出等價關系式：

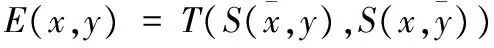
(3)

并將其作為相似測度對樣本進行分類，運用在疾病診斷中，該方法得到了較好的分類效果，但需事先確定類別的個數。ART神經網絡雖然解決了“適應性”與“穩定性”兩難的問題，但其分類性能受訓練樣本輸入順序的影響。為此，有學者將ART神經網絡與等價關系式(式(3))相結合，提出基于Yu范數的ART神經網絡模型[9]：

(1)模式選擇。假設有N個模式節點，第i類模式節點的權重向量Vi=(Vi(1)，Vi(2)，…，Vi(D))，則輸入樣本矢量與該模式節點的相似度為

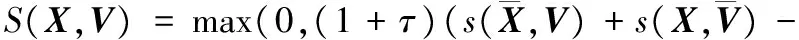
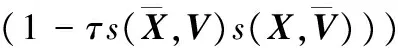
(4)

s(X,V)=min(1,f(X+V+τX×V))

(5)

式中，X、V為D維向量，X、V內的元素均為0、1之間的數；I為D維向量，向量內的元素均為1；f(Z) 表示取向量Z中各元素的平均值。

然后通過

s(X，VJ)>s(X，Vj)

J，j=1，2，…，N且j≠J

式中，VJ為獲勝模式節點的權重向量。

得到相似度最大的模式節點，即獲勝模式節點。

(2)模式匹配。根據式(4)可以得到獲勝節點J與輸入樣本向量之間的相似度s(X，VJ)，然后將其與警戒參數ρ進行比較。如果s(X，VJ)>ρ，即模式發生匹配，則表示該輸入樣本矢量被分類于該模式節點所代表的類；否則就重新建立一個新的模式節點，轉入步驟(4)。

(3)權重調整。當獲勝的模式節點與輸入樣本向量之間的相似度大于警戒參數ρ時，網絡的模式節點的權重向量調整為

VJ=(nVJ0+X)/(n+1)

(6)

式中，VJ0為原始的模式節點的權值矢量；VJ為學習過后的權值矢量；n為屬于模式節點J所代表的類的樣本個數。

(4)建立新模式節點。如果輸入樣本A與模式節點J的相似度小于警戒參數ρ，即s(X，VJ)<ρ，則需重新建立一個新的模式節點，其權值向量為

Vn+1=A

(7)

2.2 引入軟競爭的Yu范數ART神經網絡

Yu范數ART神經網絡采用勝者為王的硬競爭機制對模式節點進行分類選擇，獲勝節點獨一無二。但在實際情況中，可能存在多個滿足獲勝條件的節點，采用硬競爭機制，易造成故障類邊界處的數據樣本被誤分類，降低了分類精度。為此，本文將具有靈活調整軟競爭程度和抑制噪聲優點的模糊競爭學習(fuzzy competitive learning，FCL)軟競爭方法引入Yu范數ART神經網絡模型，提出了基于FCL軟競爭的Yu范數ART神經網絡方法。

在神經網絡的競爭層中使用軟競爭機制，每次競爭產生多個獲勝節點并參與到網絡的調整中，使得競爭層中的節點盡可能多地發揮作用，提高競爭層中節點的利用率，減少神經元信息的浪費，從而降低故障類邊界處數據樣本被誤分的概率，提高分類精度。

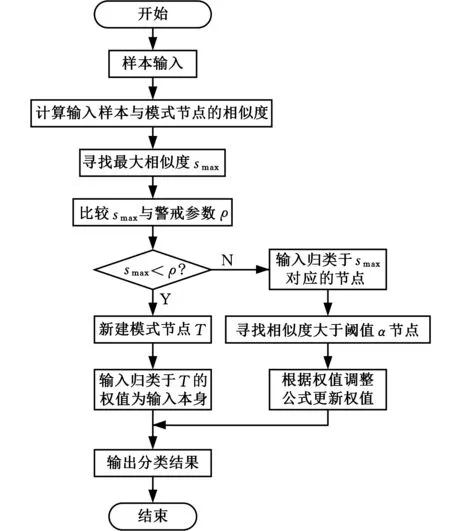
圖2 軟競爭Yu范數ART神經網絡算法流程圖Fig.2 Flow chart of Yu’s norm ART based on soft competition

網絡模型的算法如圖2所示。當輸入樣本與模式節點的相似度大于設定閾值α時，節點均為獲勝節點，并依據節點與輸入樣本間隸屬度的大小調整權值向量。與硬競爭Yu范數ART神經網絡模型的算法類似，計算輸入樣本與各個模式節點的相似度，其中,最大相似度smax所對應節點為獲勝節點，將smax與警戒參數ρ進行比較，如果smax<ρ，則新建模式節點；否則輸入樣本被分類為最大相似度對應節點所代表的類，并采用軟競爭機制，即尋找所有相似度大于閾值α的節點，對其進行權重調整，完成網絡的學習。

權重調整為

VJ=(nVJ0+hmX)/(n+hm)

(8)

(9)

式中，h為模式節點與輸入向量之間的隸屬度；c為模式節點總數；x為輸入向量；vj為當前模式節點對應的權值向量。

模糊指數m可調整軟競爭程度，m→1時，h取值為0或1，軟競爭機制退化為硬競爭機制；m→∞時，h取值為1/c，此時隸屬度最為模糊。較大的m能夠抑制噪聲，使隸屬度低的噪聲點對網絡整體的貢獻較小。

3 案例分析

3.1 數據獲取

數據為美國凱斯西儲大學電氣工程實驗室的滾動軸承數據[10]。選取負載746 W下損傷尺寸為0.1778mm(0.007英寸)的內圈、外圈以及滾動體故障，損傷尺寸為0.5334 mm(0.021英寸)的內圈、外圈故障以及正常狀態的6組數據，每種故障狀態抽取100組樣本，每組樣本有4096個采樣數據。

3.2 特征提取

對獲取的振動信號運用haar小波分析方法進行了4層分解，并分別從每層小波信號中提取了表征信號脈沖現象的峰值因子、裕度指標，以及表征信號能量變化的均方值、能量熵[11]用于刻畫軸承故障狀態。

3.3 特征優化

考慮到特征參數間的冗余性及相關性對診斷精度的影響，為提高診斷效果，對特征參數進行了優選。基于“類間距離大，類內距離小”的原則[12]，利用相似度(式(4))構建了一種特征參數優選方法[13]，具體算法如下：

(1)提取所有的特征參數，全部特征參數描述如下：

{Sn,f,p|n=1,2,…,100;f=1,2,…,6;

p=1,2,…,20}

(10)

式中，Sn，f，p為f故障下第n個樣本的第p個特征參數的值。

(2)對于任意一個特征參數p，首先計算該參數在各個模式下的類內距離

(11)

ni,nj=1,2,…,100且ni≠nj

式中，s(Sni,f,p,Snj,f,p)為特征參數Sni,f,p與Snj,f,p之間的相似度。

然后計算6種故障下的平均類內距離

(12)

(3)計算同一故障下，特征參數p的平均值，即類內中心

(13)

然后計算類與類兩兩之間的距離的平均值，即類間平均距離

(14)

fi,fj=1,2,…,6且fi≠fj

式中，s(gfi,p,gfj,p)為類內中心gfi,p與gfj,p之間的相似度。

(4)計算類間平均相似度與類內平均相似度的比值

(15)

(5)獲取各特征參數的敏感系數

λp=ep/Ep

(16)

式中，Ep為ep的最大值。

依據該算法可分別得到每個特征參數的敏感系數，系數越大說明該參數的分類靈敏度越高。在此實驗中，依據經驗設置評價系數β，敏感系數大于β的特征即為敏感特征。圖3給出了20個特征參數優化選取的結果。

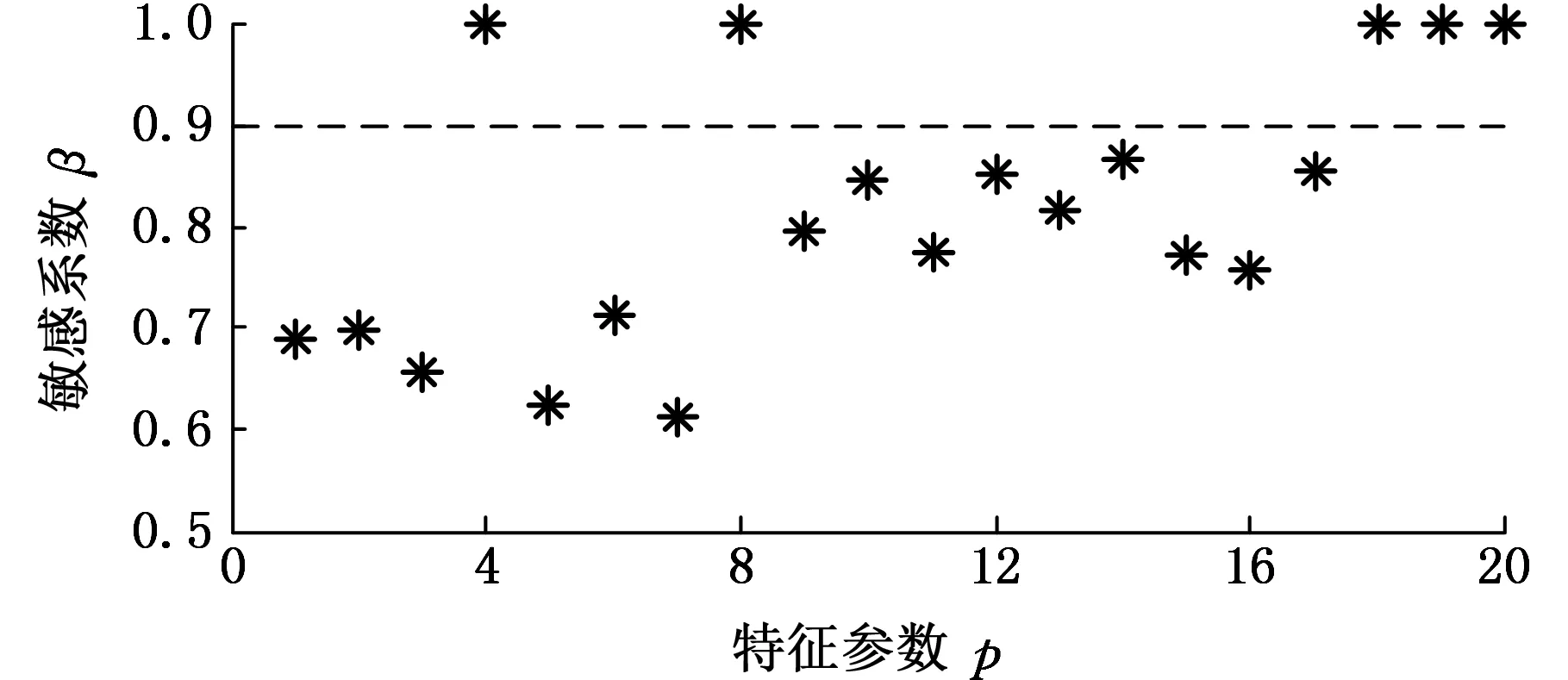
圖3 各個特征參數的敏感系數Fig.3 Sensitivity coefficients of characteristic parameters

3.4 診斷分析

該模型的特點在于分類與網絡訓練同時進行。將敏感特征參數作為故障診斷模型的輸入，當第一組樣本輸入空白網絡模型時，該樣本構建了第一個模式節點，節點權重為樣本本身。當第二組樣本輸入模型時，計算第二組輸入樣本與第一個模式節點的相似度并將其與警戒參數比較，若相似度大于警戒參數，則將第二組輸入歸類于第一個模式節點，并更新權重向量；否則依據該樣本新建第二個模式節點。當第三組樣本輸入時，計算輸入與所有節點的相似度并將最大相似度與警戒參數比較，若相似度大于警戒參數，則輸入歸類于最大相似度所對應的模式節點，且所有相似度大于閾值α的節點均為獲勝節點，計算獲勝節點與輸入間的隸屬度，根據各自隸屬度的大小更新權重向量；若小于警戒參數，則新建第三個模式節點，在分類的同時完成網絡訓練，其余樣本分類過程以此類推。在診斷過程中，根據由小到大的順序設置閾值β，進行特征參數的選擇，選擇的終止條件為診斷精度達到最高，此時閾值β=0.9。模型中參數的確定是在不改變其他參數的情況下，不斷增加目標參數值，當診斷精度達到最高時就可得到對應參數值，經分析,模型的警戒參數ρ為0.835，τ為0.4，m為6，閾值α為0.4。診斷結果如圖4所示。診斷精度為

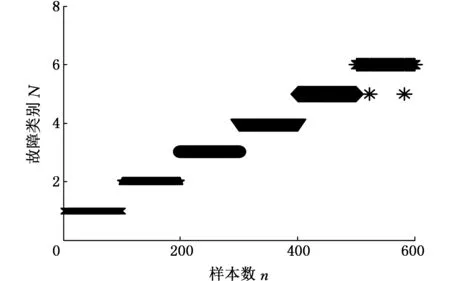
圖4 基于軟競爭Yu范數ART神經網絡分類結果Fig.4 Fig.4 Classification result of Yu’s norm ART based on soft competition

(17)

式中，C為正確分類樣本個數；T為樣本總數；N為聚類節點數[14]。

如圖4所示，樣本總數為600，正確分類樣本個數為598，由于本文模型的分類與網絡訓練同時進行，因此聚類節點數為0。計算可得D=99.67%。由圖4和診斷精度可以看出，基于軟競爭的Yu范數ART模型不僅能有效識別不同類型的故障，而且能識別不同嚴重程度故障。

3.5 參數分析

圖5～圖8給出了各個參數取不同值時的診斷結果，可以看出，隨著參數ρ、τ的增大，模型的分類精度不斷提高，但當達到模型的極限時，分類精度反而降為0；參數α的改變對模型分類精度影響較小，在取值較大時，分類精度略微降低；參數m趨于1時，模型退化為硬競爭機制，分類精度較低，隨著m的增大，軟競爭程度不斷提高，模型的分類精度也不斷提高。因此，參數值只有在合適的區間內取值時，才能得到最高的分類精度。

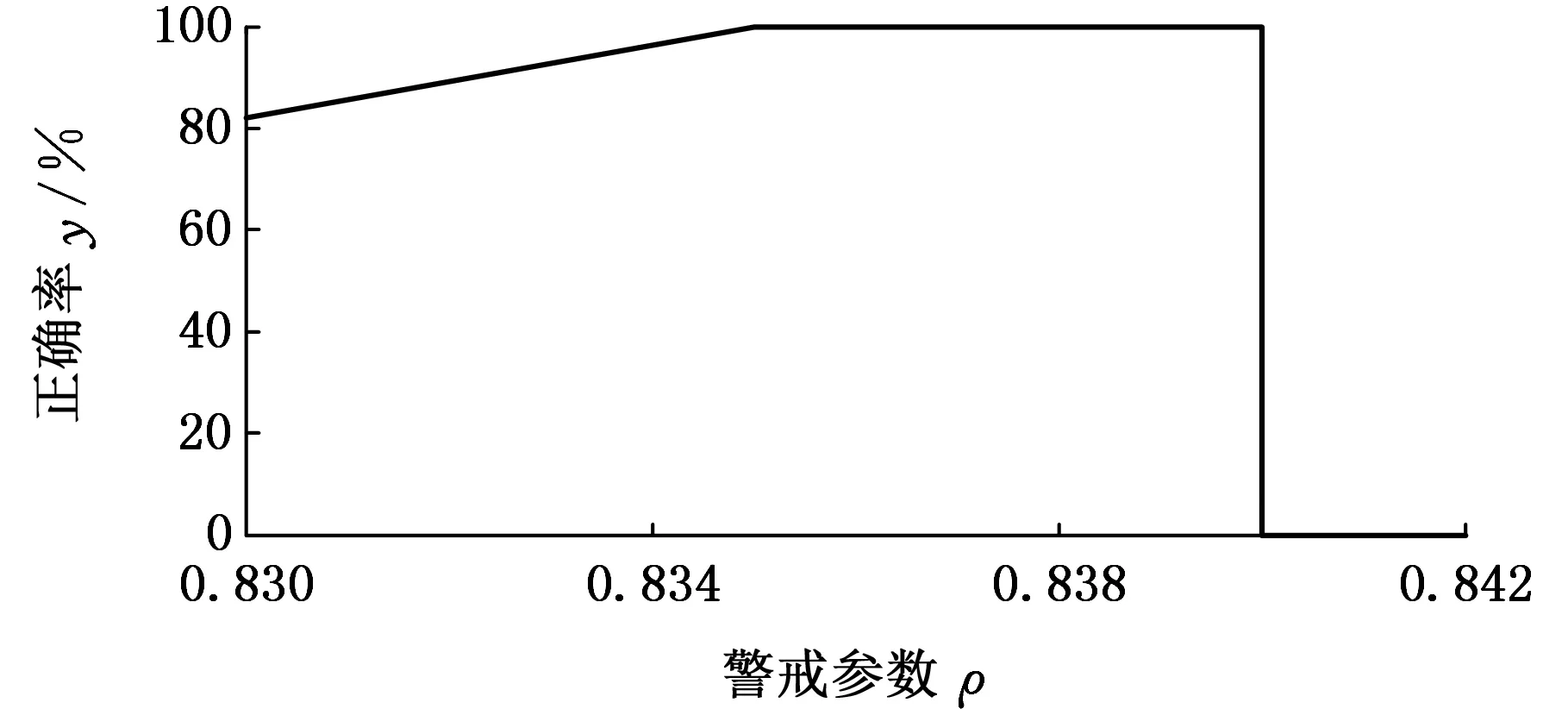
圖5 改變模型參數ρ的分類結果Fig.6 Classification result with the change of ρ

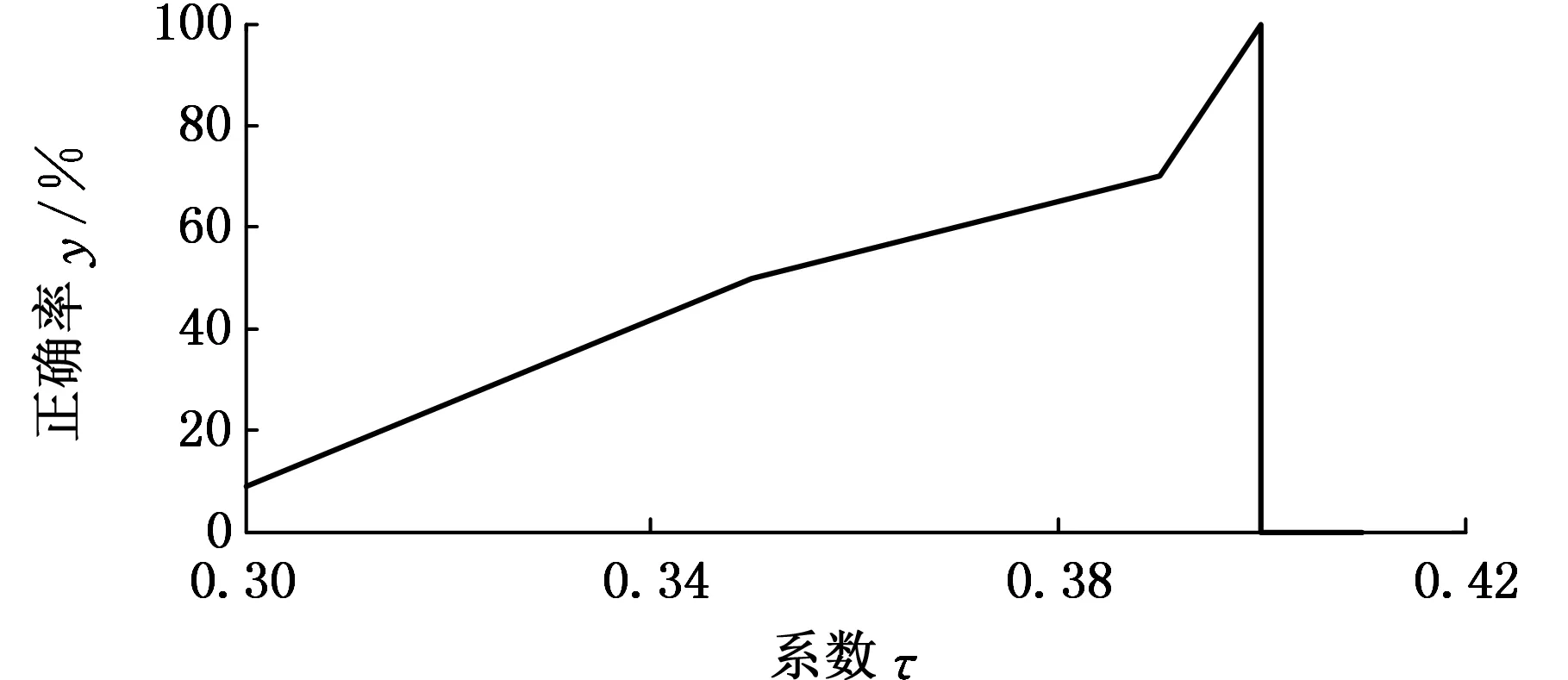
圖6 改變模型參數τ的分類結果Fig.6 Classification result with the change of τ

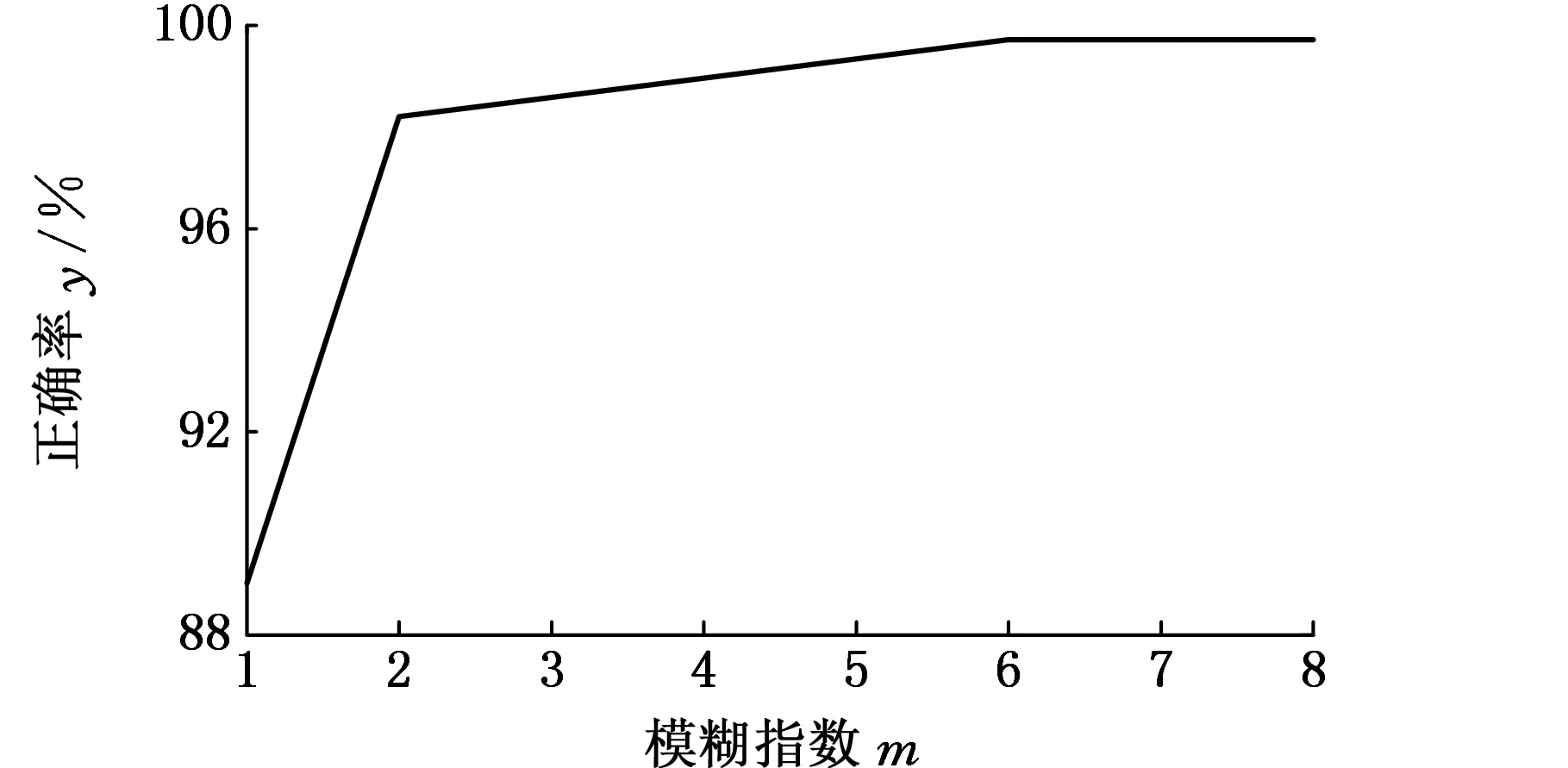
圖7 改變模型參數m的分類結果Fig.7 Classification result with the change of m

3.6 性能比較分析

為了驗證本文診斷模型的優越性，將原ART神經網絡模型、Yu范數ART模型和模糊C均值聚類模型對同樣的數據樣本進行了診斷分析，其分類結果如表1所示。由表1可以看出，模糊C均值[15]聚類的診斷精度最低，軟競爭Yu范數ART模型分類精度高達99.67%，且比硬競爭ART模型和Yu范數ART模型的分類精度分別高了16.34%和10.5%。

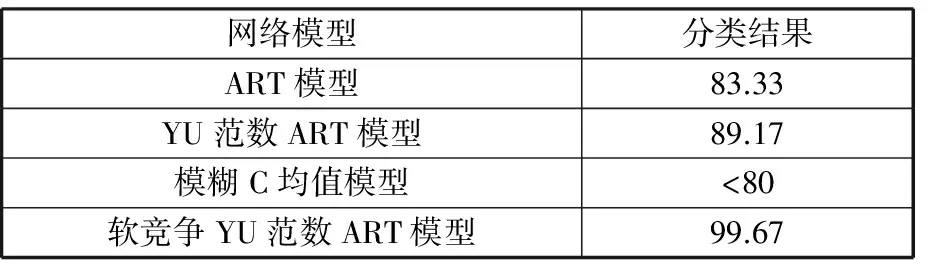
表1 模型分類結果Tab.1 Classification results of models %

4 結論

(1)軟競爭機制可以更加準確地診斷模糊區域處的數據樣本，使得基于軟競爭Yu范數ART的故障診斷方法具有更高的診斷精度。

(2)軟競爭Yu范數ART模型不僅能有效識別不同類型的故障，而且能識別不同嚴重程度故障，表明其對早期故障的診斷有著一定的效果，可以進一步探究該模型在早期故障診斷中的應用。

[1] 鄭近德，程軍圣，楊宇.多尺度排列熵及其在滾動軸承故障診斷中的應用[J].中國機械工程，2013，24(19) ：2641-2647. ZHENG Jinde，CHENG Junsheng，YANG Yu.Multi-scale Permutation Entropy and Its Applications to Rolling Bearing Fault Diagnosis[J]. China Mechanical Engineering，2013，24(19) ：2641-2647.

[2] 裴峻峰，畢昆磊，呂苗榮，等.基于多特征參數和概率神經網絡的滾動軸承故障診斷方法[J].中國機械工程，2014，25(15)：2055-2058. PEI Junfeng，BI Kunlei，LYU Miaorong，et al.Fault Diagnosis of Roller Bearings Based on Characteristic Parameters and Probabilistic Neural Network[J]. China Mechanical Engineering，2014，25(15)：2055-2058.

[3] 李勝，張培林，李兵，等.量子BP神經網絡在發動機故障診斷中的應用[J].中國機械工程，2014，25(16)：2159-2163. LI Sheng，ZHANG Peilin，LI Bing，et al. Applications of Quantum BP Neural Network in Engine Fault Diagnosis[J]. China Mechanical Engineering，2014，25(16)：2159-2163.

[4] JOU C C.Fuzzy Clustering Using Fuzzy Competitive Learning Networks[C]//International Joint Conference on Neural Networks.Miami：IEEE，1992：714-719.

[5] CARPENTER G A，GROSSBERG S.A Massively Parallel Architecture for a Self-organizing Neural Pattern Recognition Machine[J]. Computer Vision, Graphics, and Image Processing, 1987, 37:54-115.

[6] 高曉紅.ART神經網絡的發展與應用[J].電腦知識與技術(學術交流)，2007，20：509-526. GAO Xiaohong. Development and Application of ART Neural Networks[J]. Computer Knowledge and Technology(Academic Exchange) ，2007，20：509-526.

[7] YU Yandong. Triangular Norms and TNF-sigma-algebras[J]. Fuzzy Sets and Systems，1985，16(3)：251-264.

[8] LUUKKA P. Similarity Classifier Using Similarity Measure Derived from Yu’s Norms in Classification of Medical Data Sets[J]. Computers in Biology and Medicine，2007，37(8)：1133-1140.

[9] 徐增丙，李友榮，王志剛，等. 基于ART和Yu范數的聚類方法在齒輪故障診斷中的應用[J].武漢科技大學學報，2016，39(2)：116-120. XU Zengbing，LI Yourong，WANG Zhigang，et al.A Novel Clustering Method Combining ART with Yu’s Norm for Fault Diagnosis of Bearings [J].Journal of Wuhan University of Science and Technology，2016，39(2)：116-120.

[10] The Case Western Reserve University Bearing Data Center. Bearing Data Center Fault Test Data[EB/OL]. (1998-10-04).http://csegroups.case.edu/bearingdatacenter/pages/download-data-file.

[11] 王洪明，郝旺身，韓捷，等.全矢LMD能量熵在齒輪故障特征提取中的應用[J].中國機械工程，2015，26(16)：2160-2164. WANG Hongming，HAO Wangshen，HAN Jie，et al.Full Vector LMD Energy Entropy in Gear Fault Feature Extraction[J]. China Mechanical Engineering，2015，26(16)：2160-2164.

[12] 于耀亮，姜嘉言，張立明.一種新的距離測度學習算法[J].信息與電子工程，2008(2)：115-119. YU Yaoliang，JIANG Jiayan，ZHANG Liming. ANew Distance Metric Learning Algorithm[J]. Information and Electronic Engineering，2008(2)：115-119.

[13] 張任.基于振動信號的齒輪箱智能故障診斷方法研究[D].北京：北京化工大學，2013. ZHANG Ren.Intelligent Fault Diagnosis Method Research of Gearbox Based on Vibration Signal[D].Beijing：Beijing University of Chemical Technology，2013.

[14] YANG B S，HAN T，AN J L.ART-KOHONEN Neural Network for Fault Diagnosis of Rotating Machinery[J]. Mechanical Systems and Signal Processing，2004，18(3)：645-657.

[15] 王書濤，張金敏，張淑清，等.基于威布爾與模糊C均值的滾動軸承故障識別[J].中國機械工程，2012，23(5) ：595-598. WANG Shutao，ZHANG Jinmin，ZHANG Shuqing，et al. Fault Diagnosis of Rolling Bearings Based on Weibull Distribution and Fuzzy C Means Clustering Analysis[J].China Mechanical Engineering，2012，23(5) ：595-598.

(編輯 張 洋)

ISSN 1004-132X

CHINA MECHANICAL ENGINEERING

(Transactions of CMES)

Vol.28,No.14,2017 the second half of July

Semimonthly(Serial No.470)Edited and Published by:CHINA MECHANICAL

ENGINEERING Magazine Office

Add：P.O.Box 772,Hubei University of Technology, Wuhan,430068,ChinaDistributer Abroad by: China International Book

Trading Corporation (P.O.Box 399,Beijing)

Code:SM4163

Fault Diagnosis Method of Bearings by Yu’s Norm ART Based on Soft Competition

MU Hailin WANG Zhigang XU Zengbing

School of Machinery and Automation,Wuhan University of Science and Technology,Wuhan,430081

Fault interfaces were categorized wrongly by ART with hard competition. A new fault diagnosis method by Yu’s norm ART was proposed based on soft competition. The soft competition method of fuzzy competitive learning(FCL) was introduced into Yu’s norm ART, neural nodes in the competition layer were trained according to the degree of membership among the mode nodes and the inputs. Bearing fault data were used to validate the fault diagnosis model, which proves that the fault diagnosis model may distinguish different faults, and distinguish different fault degrees under the same fault types. Comparing with other methods for fault diagnosis, such as ART and fuzzy C-means clustering, the proposed method has higher diagnostic accuracy.

fault diagnosis; adaptive resonance theory(ART); soft competition; Yu’s norm

2016-09-02

國家自然科學基金資助項目(51405353)

TH17；TP183

10.3969/j.issn.1004-132X.2017.14.018

慕海林，男，1992年生。武漢科技大學機械自動化學院碩士研究生。主要研究方向為故障診斷。E-mail:285916325@qq.com。王志剛，男，1973年生。武漢科技大學機械自動化學院教授、博士研究生導師。徐增丙，男，1981年生。武漢科技大學機械自動化學院副教授。