基于密切值法的RV減速器傳動受力影響分析

鄭鈺馨,奚 鷹,李夢如,卜王輝,華濱濱,柳先輝

(同濟(jì)大學(xué) a.機(jī)械與能源工程學(xué)院; b.電子與信息工程學(xué)院,上海 201804)

?

基于密切值法的RV減速器傳動受力影響分析

鄭鈺馨a,奚 鷹a,李夢如a,卜王輝a,華濱濱a,柳先輝b

(同濟(jì)大學(xué) a.機(jī)械與能源工程學(xué)院; b.電子與信息工程學(xué)院,上海 201804)

在對RV減速器結(jié)構(gòu)簡化的基礎(chǔ)上,根據(jù)齒輪嚙合原理,采用相對運動法進(jìn)行了減速比計算,詳細(xì)闡述了擺線輪與無針齒套針齒嚙合受力分析方法.在此基礎(chǔ)上,使用密切值法,進(jìn)行了多種參數(shù)對RV傳動受力影響程度分析,確定了擺線輪厚度、曲柄軸偏心距以及針輪滾針半徑為與受力密切相關(guān)的參數(shù),在RV結(jié)構(gòu)尺寸優(yōu)化中首先考慮將這三者作為設(shè)計變量.

RV減速器; 減速比計算; 嚙合受力分析; 密切值法

RV減速器是擺線針輪減速器的一種,具有二級減速機(jī)構(gòu),一級為漸開線圓柱直齒輪傳動機(jī)構(gòu),二級為雙擺線針輪傳動,具有傳動效率高、精度高、傳遞扭矩大、傳動平穩(wěn)、體積小、質(zhì)量輕的特點,適用于精密和重載機(jī)器人.但是,其制造工藝復(fù)雜,關(guān)鍵技術(shù)嚴(yán)格保密,所以RV減速器的發(fā)展較為緩慢,成為制約工業(yè)智能化發(fā)展的關(guān)鍵因素.目前,在國外主要有兩個研究小組,分別是美國的休斯飛機(jī)公司的Blanche[1]和日本山口大學(xué)的日高照晃[2-3].國內(nèi),李力行、何衛(wèi)東、關(guān)天民等對RV減速器進(jìn)行了詳細(xì)研究,文獻(xiàn)[4-5]提出了擺線輪修型方法和擺線輪修型后受力分析方法,文獻(xiàn)[6]提出有效影響擺線針輪行星傳動承載能力3參數(shù)為偏心距、針齒套半徑以及針齒銷半徑,針對這3個變量提出了以輸出軸的定額轉(zhuǎn)矩T最大的目標(biāo)函數(shù).文獻(xiàn)[7]對傳動部分和行星架輸出機(jī)構(gòu)的誤差影響因素進(jìn)行了分析,得到傳動誤差綜合公式.文獻(xiàn)[8]對RV減速器整體施加角速度-ωh后,進(jìn)行了減速比計算,提出了在力平衡和力矩平衡條件下的擺線輪、曲柄軸以及輸出軸的受力方程,并計算了RV減速器傳動效率,證明了RV傳動效率大于單級無針齒套擺線傳動效率.文獻(xiàn)[9]指出了RV減速器和普通擺線針輪減速器在針齒結(jié)構(gòu)上的不同,提出了適用于RV減速器擺線針輪受力的分析方法.這些理論研究為RV減速器的發(fā)展打下了結(jié)實的基礎(chǔ).

本文在此基礎(chǔ)上,基于齒輪嚙合原理,首先，根據(jù)幾何關(guān)系,采用相對運動法對RV減速器減速比進(jìn)行了計算,與文獻(xiàn)[8]中反轉(zhuǎn)法相比,此方法更加直觀易于理解,但分析比較繁瑣,可以作為反轉(zhuǎn)法的對比驗證方法;其次,詳細(xì)闡述了無針齒套RV減速器擺線輪嚙合受力計算方法,并對RV-40E型減速器進(jìn)行了計算;最后,使用密切值法對多參數(shù)進(jìn)行了嚙合力影響程度排序,為RV減速器的優(yōu)化設(shè)計提供設(shè)計變量選擇依據(jù).

1 RV-40E減速器傳動分析

1.1 RV-40E減速器機(jī)構(gòu)簡化

RV-40E減速器結(jié)構(gòu)簡圖如圖1所示,兩個相同的擺線輪互為180°布置,用來平衡擺線輪傳動的偏心慣性力.兩個相同的曲柄軸,以及曲柄軸一端固結(jié)的行星輪,用來均分曲柄軸承受的載荷.

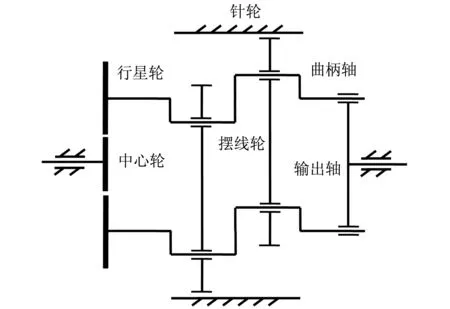
圖1 雙曲柄軸RV-40E傳動結(jié)構(gòu)簡圖

1.2 RV-40E減速器的減速比分析

減速比就是輸入軸1的轉(zhuǎn)速ω1與輸出軸5的轉(zhuǎn)速ω5之比.圖2中,擺線輪3與輸出軸5之間的連接機(jī)構(gòu)稱為“W機(jī)構(gòu)”,即擺線輪3的絕對角速度ω3與輸出軸5的轉(zhuǎn)速ω5相等.

由A點處的速度關(guān)系

有

(1)

式中:ω2r5為曲柄軸與行星輪固結(jié)件2相對于輸出軸5的轉(zhuǎn)動角速度.

由B點處的速度關(guān)系

有

(2)

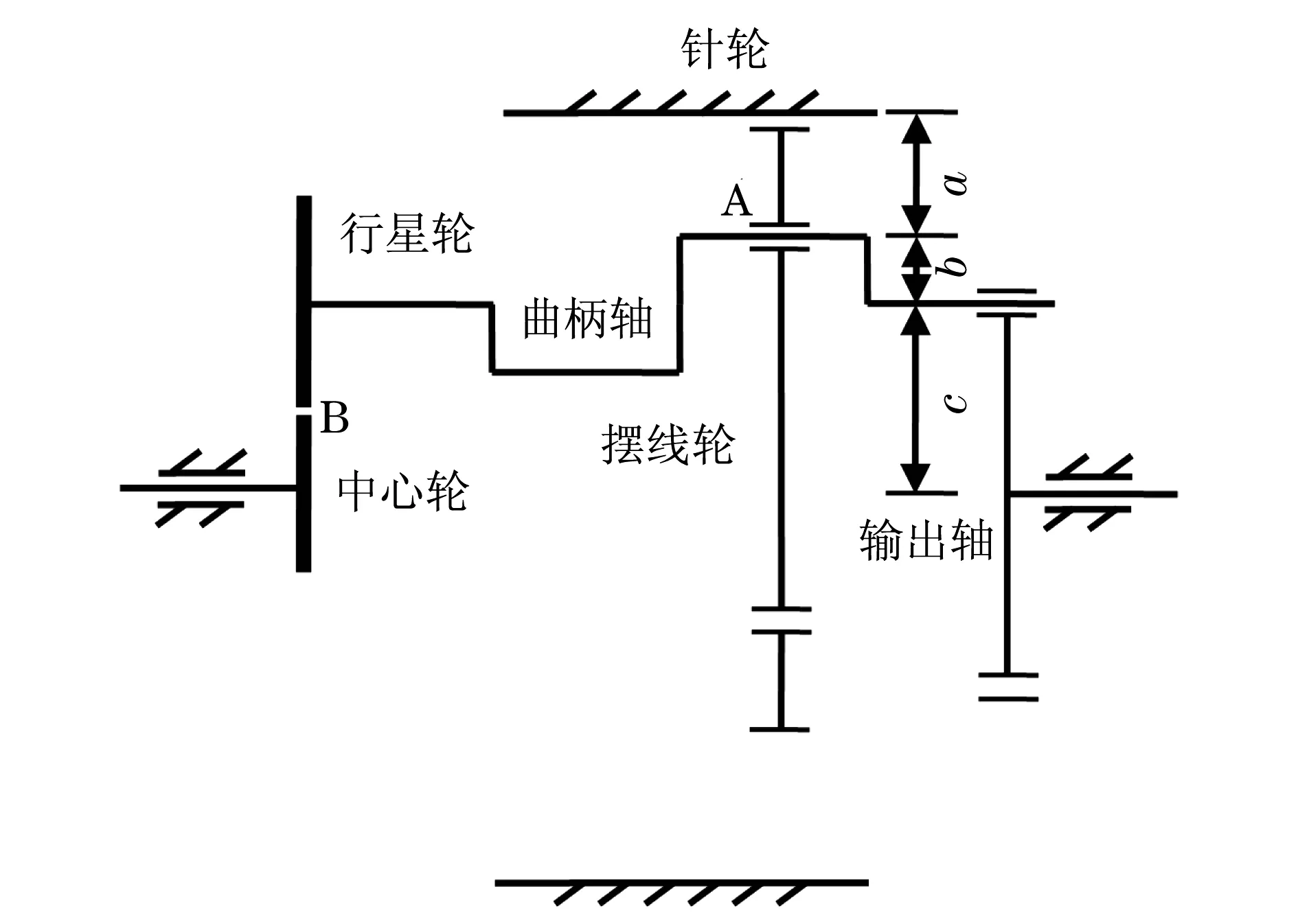
圖2 RV-40E減速比分析圖

式中:R1，R2分別為輸入軸中心輪1和行星輪2的半徑.

由于ω3=ω5,得到

(3)

因為a+b+c=R6,b=R6-R3,其中R6和R3分別為針輪6和擺線輪3的半徑,所以得到

(4)

根據(jù)齒輪嚙合原理

有

(5)

式中：Z1和Z2分別為輸入軸中心輪1和行星輪2的齒數(shù).

(6)

式中：Z6和Z3分別為針輪6和擺線輪3的齒數(shù).

有

(7)

這款RV-40E減速器的參數(shù)為Z6=40,Z1=10,Z2=26,Z3=39,因此得

(8)

即,這款RV-40E減速器的減速比為105.

2 RV-40E減速器擺線輪嚙合受力分析

2.1 RV-40E減速器基本參數(shù)

RV-40E減速器相關(guān)具體參數(shù)如下:針齒中心圓半徑rz=64 mm,針齒半徑rrp=3 mm,針輪殼內(nèi)徑rp=70 mm,偏心距e=1.3,針輪齒數(shù)zp=40,擺線輪齒數(shù)zc=39,中心輪齒數(shù)z1=10,行星輪齒數(shù)z2=26,模數(shù)m=1.25,壓力角α′=20°,中心輪轉(zhuǎn)速v1=525r/min,單片擺線輪扭矩Tc=314.6N·m,輸出轉(zhuǎn)速為v2=5r/min,速比i=105,輸出轉(zhuǎn)矩為T=572N·m,擺線輪彈性模量E=2.07×105N/mm2,泊松比μ=0.254,針齒E=2.08 ×105N/mm2,泊松比μ=0.3,外殼彈性模量E=1.68 ×105N/mm2,泊松比μ=0.24,擺線輪厚度bc=8.86mm.

2.2 RV-40E擺線輪與針齒嚙合受力分析

標(biāo)準(zhǔn)擺線輪以及只經(jīng)過轉(zhuǎn)角修型的擺線輪與標(biāo)準(zhǔn)針輪嚙合,在理論上可以達(dá)到同時嚙合的齒數(shù)為擺線輪齒數(shù)的一半,但擺線輪齒型經(jīng)過等距、移距或等距加移距復(fù)合修形,如果不考慮零件彈性變形補償作用,則只能存在一個齒嚙合,其余的擺線輪輪齒與針齒之間都存在著大小各不相同的初始間隙,其嚙合法線方向的初始間隙Δ(φi)根據(jù)文獻(xiàn)[7-8]計算如下:

(9)

式中:φi為第i各針齒相對于轉(zhuǎn)臂的轉(zhuǎn)角(°),0≤φi≤180°;k為短幅系數(shù),k=ezp/rz=0.812 5;a為移距修型量(mm),a=0.008;b為等距修型量(mm),b=-0.002;e為曲柄軸偏心距,e=1.3 mm.

由于RV-40E的針輪為40個齒,所以360/40=9,即每9°分布一個齒,如圖3所示.

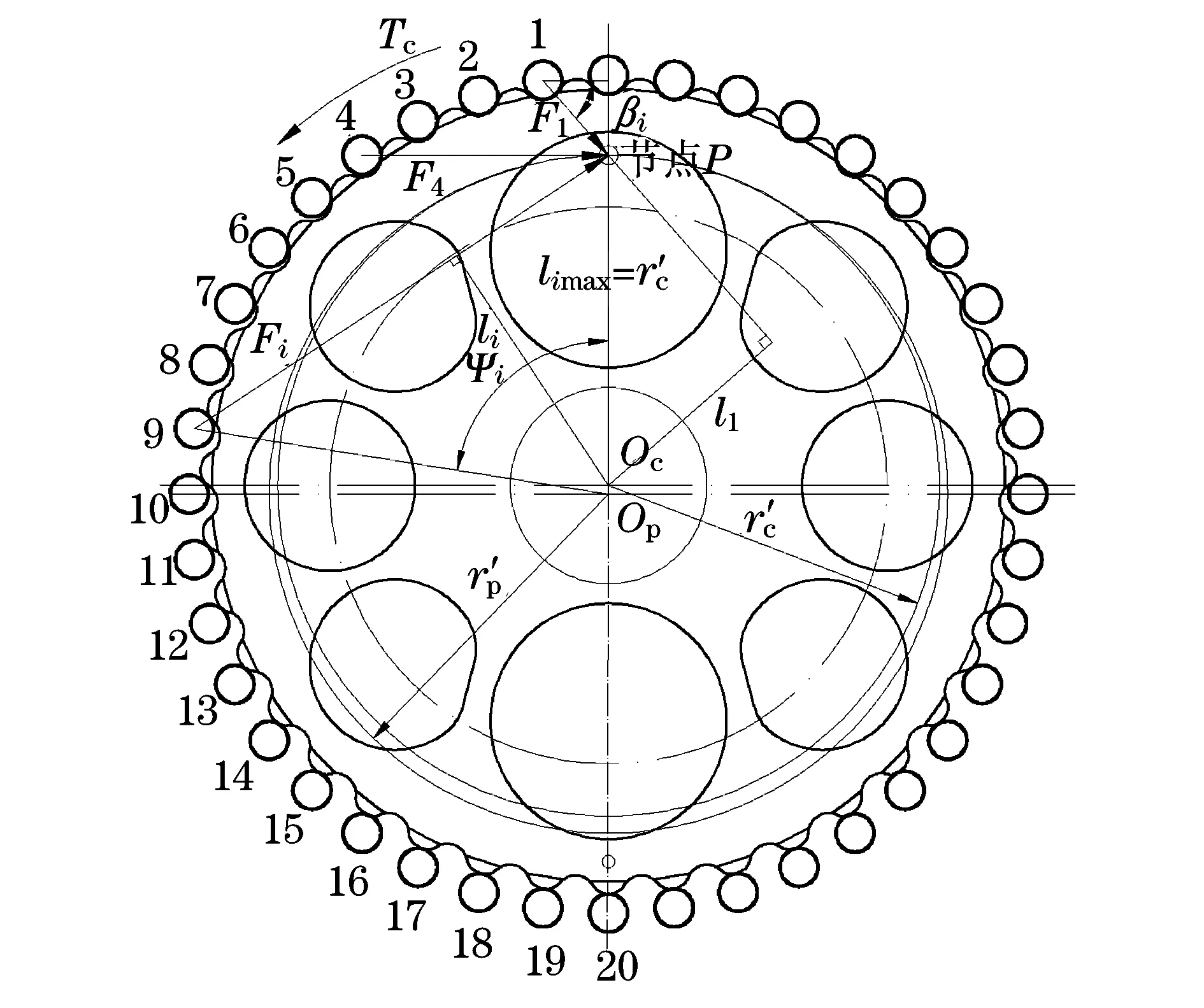
圖3 擺線輪嚙合受力圖

但考慮彈性變形情況下,對擺線輪施加力矩時,擺線輪與針齒會產(chǎn)生接觸變形,將接觸變形分兩部分：一是擺線輪輪齒與針齒嚙合時的接觸變形ω1;二是針齒與針輪殼之間的接觸變形ω2.當(dāng)這兩種變形量大于初始間隙時,就會產(chǎn)生多齒嚙合情況.根據(jù)RV傳動裝置的特點,知兩者是在相同的嚙合力作用下同時產(chǎn)生的,共同影響擺線輪的嚙合力大小.根據(jù)赫茲公式,長以L(L=bc)的圓柱與圓柱接觸時,其接觸變形為

式中:F為兩圓柱之間的作用力(N);E1,E2為兩圓柱的彈性模量(N/mm2);R1,R2為兩圓柱的半徑(mm);μ1,μ2為圓柱的泊松比.

(11)

當(dāng)圓柱與圓柱凸凸面接觸時,當(dāng)量曲率半徑為

(12)

當(dāng)圓柱與圓柱凸凹面接觸時,當(dāng)量曲率半徑為

(13)

擺線輪實際齒廓曲線的曲率半徑為

當(dāng)擺線輪和針齒接觸時,

(15)

當(dāng)針齒和針輪殼接觸時,

(16)

每一個嚙合位置同時有兩個變形量,所以,ω=ω1+ω2,在求得每個位置的變形量后,得到其中最大變形量ωmax.

在彈性變形條件下,嚙合力法向上的位移為

式中:β為加載后由零件變形而引起的擺線輪的轉(zhuǎn)角(°);li為第i個嚙合點的公法線或待嚙合點的法線至擺線輪中心Oc的距離(mm),如圖3所示;r′c為擺線輪的節(jié)圓半徑(mm),r′c=ezc;δmax為嚙合處最大變形量(mm),δmax=ωmax.

當(dāng)δi-Δ(φ)i>0時,相對應(yīng)的齒數(shù)i嚙合,并且其嚙合力表達(dá)式如下:

式中:Tc為一片擺線輪傳遞的轉(zhuǎn)矩(N·mm),Tc=0.55T;T為輸出軸上阻力矩(N·mm).

最大嚙合力的初始值描述如下:

在無間隙、嚙合時,最大的嚙合力為

(21)

有間隙時、嚙合時,最大的嚙合力為

(22)

而真正的嚙合狀態(tài),處于這兩者之間,所以,最大初始嚙合力大小為

(23)

以式(23)為初值,帶入式(9)～(20),得到按照Fmax,并按照下面判別式(24),通過迭代得到更加符合實際的初始值

(24)

通過Matlab編程計算得到,RV-40E減速器的嚙合區(qū)間為2～11個齒,最大初始嚙合力為Fmax=1 284.6N.通過迭代計算后,得到的最大嚙合力為1 190.8N,出現(xiàn)在第4個針齒附近,并且,通過(arccsc0.812 5)/9=3.962,可知,最大嚙合力的理論出現(xiàn)位置也是第4個齒.

擺線輪接觸應(yīng)力為

(25)

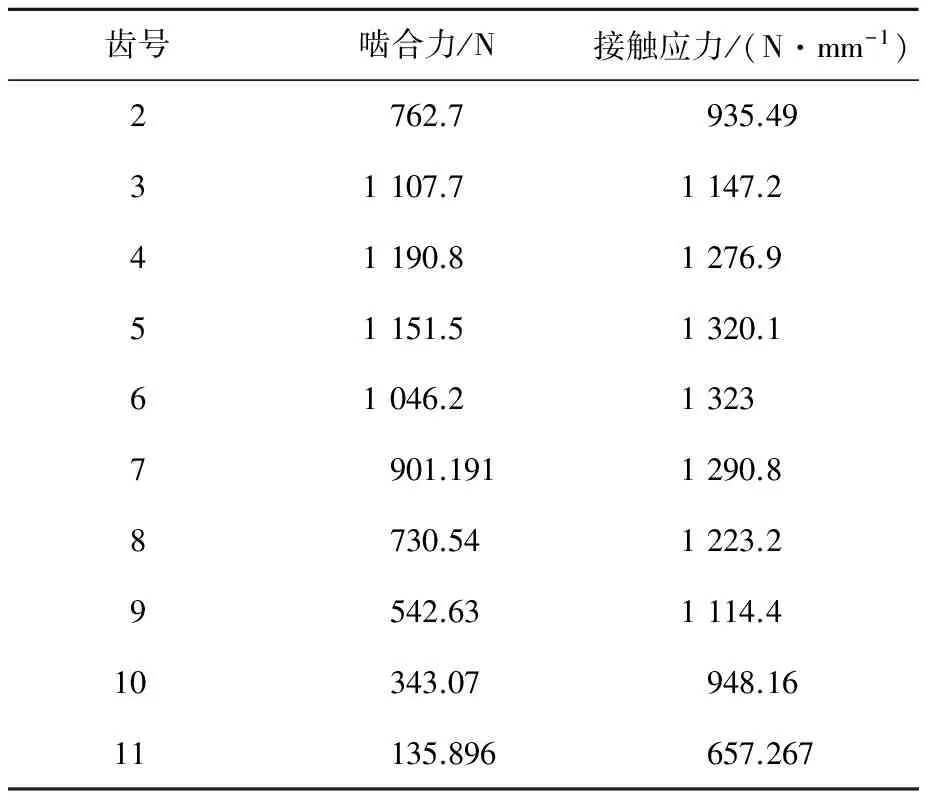
表1 理論計算嚙合力和接觸應(yīng)力

2.3 RV-40E擺線輪與針齒嚙合合力計算

當(dāng)Fi與x軸的夾角為βi時,如圖3所示,則有

(26)

(27)

(28)

通過計算,Fx=7 422.005 N,Fy=1 245.9 N,Fx,Fy為作用在一個擺線輪上的各針齒嚙合力在X,Y方向上的合力.

3 基于密切值法的參數(shù)影響系數(shù)分析

從式(9)～(28)可知,針輪滾針半徑、移距修型量、等距修型量、擺線輪厚度和曲柄軸偏心距是影響擺線輪嚙合力大小的重要參數(shù).根據(jù)密切值法,要建立n×m的原始指標(biāo)矩陣,其中n為需要進(jìn)行排序的參數(shù),m為評價指標(biāo).當(dāng)參數(shù)值變化相同數(shù)值0.001 mm時,最大嚙合力的變化值并不能作為影響程度排序的單一指標(biāo),還需將原始值、材料的彈性模量、工藝實現(xiàn)難易程度作為衡量指標(biāo),如表2所示.

矩陣模型的規(guī)范化后為表3.則最優(yōu)點集合為

G={0.467 6,0.448 5,0.938 2,0.448 9,0.545 5}

則最劣點集合為

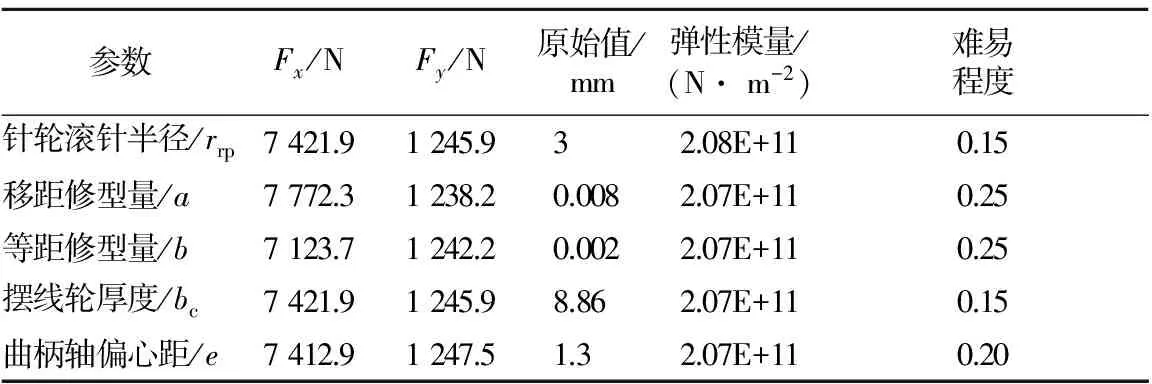
表2 原始指標(biāo)矩陣

表3 規(guī)范化指標(biāo)矩陣

則各評價單元與最優(yōu)評價點和最劣評價點的密切系數(shù)為表4.

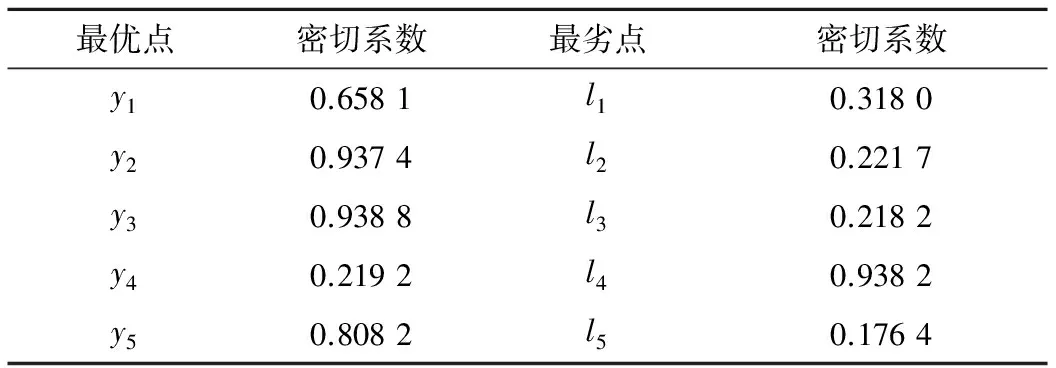
表4 評價單元的密切系數(shù)

密切值是無量綱值,以C表示,它以各評價單元與最優(yōu)點的最小距離和與最劣點的最大距離作為參比,綜合比較其隸屬于最優(yōu)點和最劣點親疏程度.當(dāng)C值越小,則被評單元與最優(yōu)點關(guān)系越密切,與最劣點關(guān)系越疏遠(yuǎn).當(dāng)C=0,被評單元指標(biāo)值在的所有參評單元中達(dá)到最優(yōu).通過表5可知,在綜合考慮情況下,擺線輪厚度、曲柄軸偏心距以及針輪滾針半徑三者對RV減速器受力影響較大,在RV優(yōu)化設(shè)計中,優(yōu)先考慮這3個參數(shù).

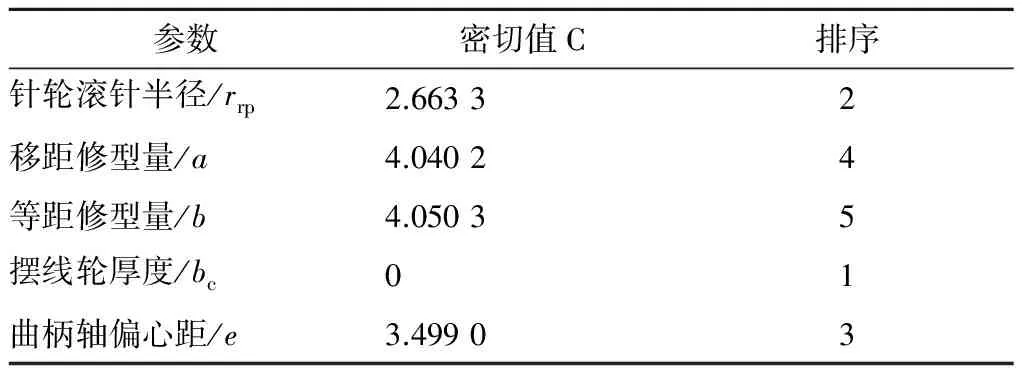
表5 評價單元的密切值及排序

4 結(jié)論

(1) 根據(jù)齒輪嚙合傳動原理,使用相對運動法對RV減速器的減速比進(jìn)行了計算,所得結(jié)果與RV-40E實際減速比一致,此方法較為復(fù)雜,但相對于反轉(zhuǎn)法更易于理解和掌握.

(2) 進(jìn)行了擺線輪和無針齒套針齒的嚙合受力分析,對RV-40E進(jìn)行了詳細(xì)計算,為動力學(xué)分析奠定了基礎(chǔ).

(3) 在嚙合受力分析基礎(chǔ)上,運用密切值法分析了各參數(shù)對嚙合受力的影響,此方法采用統(tǒng)計學(xué)概念,對影響程度進(jìn)行排序,簡單方便可靠,所得結(jié)論可以用于RV優(yōu)化設(shè)計中.

[1] BLANCHE J G,YANG D C H.Cycloid drives with machining tolerances[J].Journal of Mechanisms,Transmissions,and Automation in Design,1989,111(9):337-344.

[2] 石田武,王宏猷,日高照晃,ほか.サイクロイド齒車を用ぃたK-H-V形遊星齒車裝置の回轉(zhuǎn)傳達(dá)誤差に開する研究(第2報,各種加工誤差、組立誤差が回轉(zhuǎn)傳達(dá)誤差に及ほす影響)[J].日本耭械學(xué)會論文集(C編),1994,60(578):278-285.

ISHIDA T,WANG Hongyou,HIDAKA T,et al.Rotational transmission error of K-H-V planetary gears with cycloid gear(2nd report,effects of manufacturing and assembly error)[J].JSME International Journal:Serises C,1994,60(578):278-285.

[3] 日高照晃,王宏猷,石田武,ほか.サィクロィド齒車を用ぃた K-H-V形游星齒車裝置の回轉(zhuǎn)連誤差に開する研究(第1報:解析方法)[J].日本機(jī)械學(xué)會論文集(C編),1994,60(570):645-653.

HIDAKA T,WANG Hongyou,ISHIDA T,et al.Rotational transmission of K-H-V plantary gears with cycloid gear(1st report,analytical method of the rotational transmission error)[J].JSME International Journal:Serises C,1994,60(570):645-653.

[4] 李力行.擺線針輪行星傳動的齒形修正及受力分析[J].大連鐵道學(xué)院學(xué)報,1984,4:29-39.

LI Lixing.The modification manner for tooth profile and the analysis of forces on the cycloid disk of a cycloid speed reducer[J].Journal of Dalian Institute of Railway Technology,1984,4:29-39.

[5] 李力行,洪淳赫.擺線針輪行星傳動中擺線輪齒形通用方程式的研究[J].大連鐵道學(xué)院學(xué)報,1992,13(1):7-11.

LI Lixing,HONG Chunhe.The general equations for the teeth profile of cycloidal gear[J].Journal of Dalian Institute of Railway Technology,1992,13(1):7-11.

[6] 李力行,關(guān)天民,王子孚.擺線針輪行星傳動的計算機(jī)輔助設(shè)計[J].大連鐵道學(xué)院學(xué)報,1992,13(1):26-33.

LI Lixing,GUAN Tianming,WANG Zifu.The computer aided design of cycloid gearing[J].Journal of Dalian Institute of Railway Technology,1992,13(1):26-34.

[7] 李力行,何衛(wèi)東,王秀琦.機(jī)器人用高精度RV傳動的研究[J].大連鐵道學(xué)院學(xué)報,1999,20(2):2-10.

LI Lixing,HE Weidong,WANG Xiuqi.The study on high-accuracy RV drive used in robot[J].Journal of Dalian Railway Institute,1999,20(2):2-10.

[8] 何衛(wèi)東,李力行.RV傳動的效率及其受力分析[J].大連鐵道學(xué)院學(xué)報,1992,13(1):73-81.

HE Weidong,LI Lixing.Analysis on the forces and efficiency of RV reducer[J].Journal of Dalian Institute of Railway Technology,1992,13(1):73-81.

[9] 何衛(wèi)東,李力行.機(jī)器人用RV傳動中擺線輪受力分析[J].大連鐵道學(xué)院學(xué)報,1999,20(2):49-53.

HE Weidong,LI Lixing.Force analysis on cycloidal gear of the RV drive used in robot[J].Journal of Dalian Railway Institute,1999,20(2):49-53.

Original error analysis on the second reduction part of RV reducer

ZHENG Yuxina,XI Yinga,LI Mengrua,BU Wanghuia,HUA Binbina,LIU Xianhuib

(a.School of Mechanical Engineering; b.School of Electronics and Information Engineering,Tongji University,Shanghai 201804,China)

On the basis of RV reducer structure simplification,according to the principle of gear meshing,a relative motion method is used for RV reducer reduction ratio calculation,a meshing force analysis method of cycloid gear with no sleeve pin gear is expounded,and on this basis,using osculating value method,an analysis of various parameters influence on RV transmission force is made,and get a conclusion that the thickness of cycloid gear,the eccentricity of crankshaft and the radius of roller are closely parameters related to the transmission force.In structural optimization,the three parameters are considered as design variables preferentially.

RV reducer; the reduction ratio calculation; meshing force analysis; osculating value method

國家自然科學(xué)基金資助項目(51475331);中央高校基本科研業(yè)務(wù)費專項基金資助項目(20153712);上海市科技創(chuàng)新計劃資助項目(15111102702)

鄭鈺馨(1989—),女,博士生.E-mail:zhengyuxin1989@126.com

TP 242.2

A

1672-5581(2017)02-0153-05