二輪數理融合需自我加壓的幾個方面

湖北 朱木清

二輪數理融合需自我加壓的幾個方面

湖北 朱木清

高考物理“五種能力”中，應用數學處理物理問題的能力，是考查區分的重點。為應對這一問題，各校一般會在二輪后期安排一個專題復習。但僅依賴一次短期突擊是遠遠不夠的，重要的還在于激發內在動力，把提升數理融合目標變成個體的自覺行動，貫穿于全過程，落實到訓練中。為此，建議同學們在以下幾個方面自我加壓。

一、主動梳理物理解題常用的數學知識和方法

圖1

【解析】先分析導線a的受力，題設a、b平行，電流分別為I和2I，此時a受到的磁場力大小為F。再在a、b的上方放置一根與a、b平行的通電長直導線c，a、b、c正好構成一個等邊三角形，a受到的磁場力大小仍為F，根據平行四邊形定則，可知c對a的磁場力Fca方向由a指向c，大小等于F，如圖2所示。

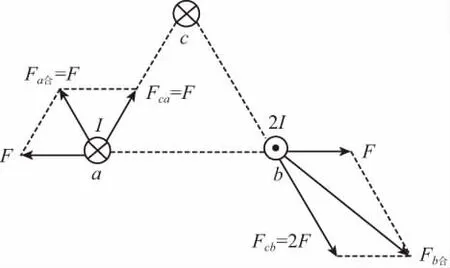
圖2

再分析b的受力，a對b的磁場力大小為F，因為rca＝rcb，a、b電流分別為I和2I，所以c對a的磁場力大小Fca＝F，故c對b的磁場力大小Fcb＝2F，根據平行四邊形定則和余弦定理，可得b受到的磁場合力大小為Fb合＝，D項正確。

【答案】D

【點評】矢量的平行四邊形定則本身就是一個幾何圖形。本例要用到余弦定理，在解題中不常用。課標卷物理注重數學知識應用的廣度和深度，淡化煩瑣數學計算，代數方程、函數分析、解析幾何、三角函數、指數對數、導數微分等均已滲透物理教材，幾何法、圖象法、極限極端法、極值法、微元法、轉化法、半定量與估算法等數學方法成為高考的“常客”，若將這些數學知識方法做些梳理，具體細化，解題很給力。

二、重視解題中輔助關系方程的分析

【例2】水平面上A、B、C三點固定著三個電荷量均為Q的正點電荷，將另一質量為m的帶正電的小球（可視為點電荷）放置在O點，OABC恰好構成一棱長為L的正四面體，如圖3所示。已知靜電力常量為k，重力加速度為g，為使小球能靜止在O點，小球所帶的電荷量q為 （ ）

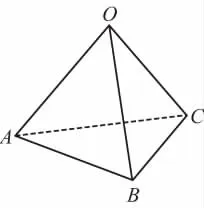
圖3

【解析】O處小球受到A、B、C三個點電荷的庫侖力大小均為，方向沿正四面體側棱，將庫侖力F正交分解，根據平衡條件和對稱性，它們的水平合力為零，豎直合力跟小球重力平衡。

設F與水平方向夾角為α，有3Fsinα＝mg，如圖4所示，底面垂心H到頂點A或B的距離，聯立解得

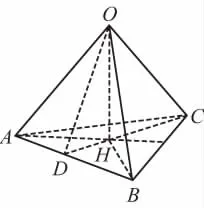
圖4

【答案】C

【點評】本題牽涉到正四面體側面與底面所成的二面角，側棱與底面的夾角α，容易誤以為都是60°，混淆側棱與底面夾角與二面角關系，從而錯選A項或B項。物理解題經常涉及這樣的輔助關系。平時練習中，常見到所列物理方程都對，但輔助方程卡殼或出錯，十分可惜。因此，列輔助方程非但不能小視，而且在接下來的訓練中還應加強。

三、重視物理難點中的數學破解以及數學對物理的詮釋

【例3】如圖5所示，小車用跨越定滑輪的輕繩牽引提升井下重物。某時刻小車和物體的速度大小分別為v1和v2，加速度大小分別為a1和a2，細繩與水平地面夾角為θ，則下列關系式正確的是 （ ）

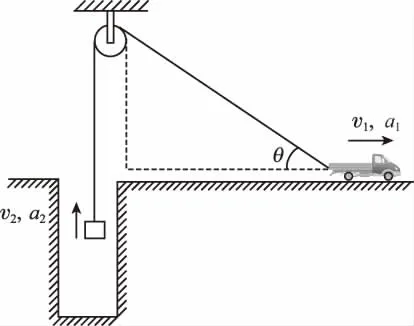
圖5

A．v1cosθ＝v2B．v1＝v2cosθ

C．a1cosθ＝a2D．a1＝a2cosθ

【解析】設時間Δt內小車向右的位移為Δx，斜繩長度變化為Δs，物體提升高度變化Δh＝Δs，斜繩傾角變化Δθ，如圖6所示，故有 Δxcosθ＝Δs，等式兩邊同除以 Δt，并取Δt→0，得v1cosθ＝v2，A項正確，B項錯誤。

圖6

在關系式v1cosθ＝v2中，v1、v2和θ均隨時間t變化，等式兩邊同時對時間t求導，有

【答案】A

【點評】我們知道，對有轉動的繩或桿，兩端牽連體沿繩或桿方向的分速度總等大，但加速度關系就不那么簡單，也是個“擦邊球”，上述數學推導結果給我們以啟示：小車的運動可看成兩個分運動：一是以滑輪為中心、斜繩長為半徑的變速圓周運動（速度的大小和方向都變化），另一是沿斜繩伸長或縮短方向的運動。

如圖7所示，小車的加速度分量a1cosθ方向沿繩方向，但它并不等于斜繩的伸長或縮短產生的沿繩方向加速度分量ar，還包含了繞滑輪做變速圓周運動的向心加速度分量an，二者的矢量和滿足a1cosθ＝ar－an。

圖7

需注意，當繩有轉動，牽連體垂直繩方向的分速度不為零時，因繞定滑輪轉動存在向心加速度（方向沿繩向），重物的加速度a2與小車的加速度沿繩方向的分量a1cosθ不等，二者加速度關系為a2＝a1cosθ±an（式中符號“±”跟小車加速運動的方向有關，如小車向左加速，則取“＋”號）；僅當繩無轉動，牽連體垂直繩方向的分速度為零時，才有兩端牽連體沿繩方向加速度分量等大。

【例4】如圖8所示，在xOy平面內的y軸右側，虛線包圍圓形區域為真空，圓半徑為L，圓心在O1（2L，0）處，x＝0～3L區間除虛線包圍圓形區域，其余部分有垂直紙面向外的勻強磁場，磁感應強度為B。一質量為m、帶電量為＋q的粒子從y軸某點垂直y軸射入磁場，不計粒子重力作用。

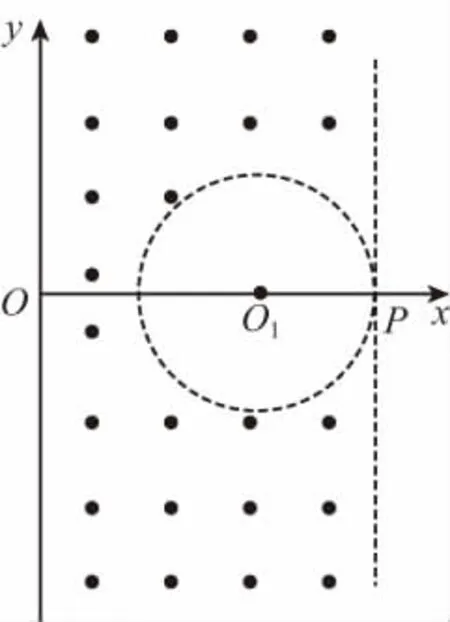
圖8

（1）若粒子經過x軸上P點，求其入射的位置和速度大小；

（2）若粒子經過圓形區域中心O1點，求入射速度最小值。

【解析】（1）粒子在勻強磁場中做勻速圓周運動，有

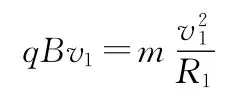
若粒子經過x軸上P點，則入射的位置坐標為（0，3L），圓軌道半徑R1＝3L，入射速度大小

（2）若粒子經過圓形區域中心O1點，必是先在磁場中做一段圓弧運動，再沿真空圓半徑方向勻速運動到O1點，設粒子圓弧運動的軌道中心為O2，軌道半徑為R，圓弧中心角為θ，幾何位置關系如圖9所示，同理有

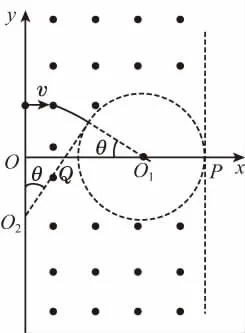
圖9

欲v最小，必須R最小，而

【點評】求解物理極值題，通常有物理和數學兩種方法，但本題必須借助數學方法。同學們對三角函數求極值、二次函數求極值、均值不等式求最值等方法玩得都很酷，但這里求分式函數極值是個難點，導函數為零是否能想到？物理問題的分析過程，就是數學方法的運用過程，數學用活了，物理也活了。

（作者單位：湖北省武漢市黃陂區第一中學）