一道力學綜合題的多種解法

河北 董鳳娥

一道力學綜合題的多種解法

河北 董鳳娥

一題多解是培養學生準確理解和靈活運用物理規律及方法的有效途徑，也是培養學生發散思維的方式之一，更是提高復習效率的有效方法。現以一道典型力學綜合題為例，說明一題多解在學習中的作用。

【題目】如圖1所示，C是放在光滑水平面上的木板，質量為3m，在木板上面有兩塊質量均為m的小木塊A和B，它們與木板間的動摩擦因數均為μ。最初木板靜止，A、B兩木塊同時分別以水平向右的初速度v0和2v0在木板上滑動，木板足夠長，A、B始終未滑離木板。求：

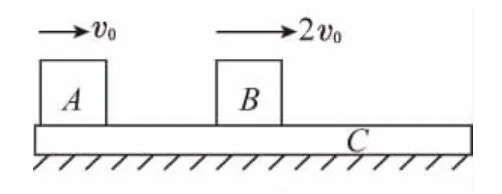
圖1

（1）木塊B從剛開始運動到與木板C速度剛好相等過程中，木塊B所發生的位移；

（2）木塊A在整個過程中的最小速度值。

【解析】這是一道經典的力學問題，經常出現在考試中，其考查的知識涉及高中力學的絕大多數重點內容，思維發散，非常值得我們研究。

首先，我們分析一下題設條件。光滑水平面意味著對于木板C和木塊A、B組成的系統來說，在水平方向上不受任何外力，所以系統動量守恒；又因為木板足夠長，A、B始終未滑離木板，這意味著三者最終具有相同的速度v。故有

其次，結合題意可知，在整個運動過程中，小木塊A和B與木板C發生相對運動，會受到木板給它們的向左的摩擦力，大小為μmg；而木板受到向右的摩擦力，大小為2μmg。木塊A向右做勻減速直線運動，因木塊A的初速度小，故木塊A的速度首先減小到和木板C具有同樣大小的速度，此時它的速度就是在整個運動過程中的最小速度，然后隨木板做勻加速直線運動；當木塊B的速度也減小到與木板C的速度相同時，此時木塊B發生的位移就是第一問要求的位移；然后三者相對靜止一起向右做勻速直線運動。木塊C可以看成先做兩段加速度不同的勻加速直線運動，最后向右做勻速直線運動。

到此，我們不難發現第一問所要求的問題：應該是當B的速度減小到與木板C的速度相同時，即三者從開始相互作用到三者相對靜止時，木塊B在木板C上發生的相對位移的大小。對木塊B運用動能定理，有

第二問所要求的問題是木塊A在整個過程中的最小速度值，應當是當木塊A的速度首先減小到與木板C的速度剛好相等時的木塊A的速度值。具體求解可采用以下幾種方法。

方法一：用動量守恒定律求解

當木塊A的速度首先減小到與木板C的速度剛好相等時，A的速度最小。設最小速度為v′，則B的速度為v0＋v′，由動量守恒定律有

mv0＋2mv0＝mv′＋m（v′＋v0）＋3mv′，

【點評】利用整個系統動量守恒解決問題，僅僅考慮A、B、C的初始狀態和A的速度最小時A、B、C的末狀態，不涉及中間過程，體現動量守恒定律解題的簡捷性。

方法二：用動量定理求解

設木塊A在整個過程中的最小速度為v′，達到v′的時間為t，

對木塊A：μmgt＝mv0－mv′①

對木板C：2μmgt＝3mv′②

【點評】此方法對A、C用了動量定理，僅考慮A、C的初始狀態和A的速度最小時A、C的末狀態，也沒有涉及中間過程，同樣簡單明了。

方法三：用牛頓第二定律求解

設木塊A在整個運動過程中的最小速度為v′，達到最小速度所用的時間為t，注意此時木板受到的摩擦力大小是2μmg，由牛頓第二定律可得

對木塊A：由μmg＝ma1得a1＝μg。

當木塊A與木板C速度相等時A的速度最小，故有v0－a1t＝a3t，即

【點評】運用牛頓第二定律解決問題，涉及受力分析，注重分析過程，明確A、C的運動情況，過程分析詳細，這說明分析物理過程很重要。

方法四：用動能定理求解

設木塊A在整個運動過程中的最小速度為v′，達到最小速度所用的時間為t，

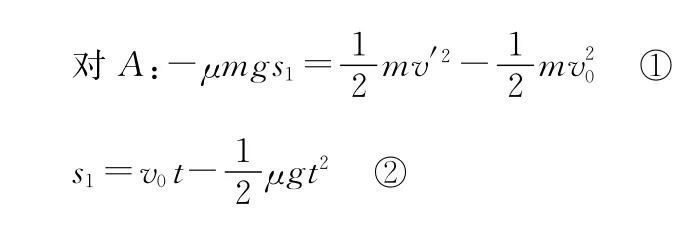
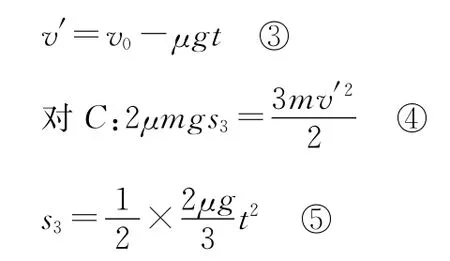
【點評】此法站在能量轉化和運動學的角度處理問題，看似復雜但更有物理“味”，再次說明詳細分析物理過程的重要性。

通過上述解法不難看出，解決這類問題時，整體把握用動量守恒定律和動量定理，局部把握用牛頓運動定律和動能定理（或功能關系）。在平時的學習或復習中，我們要注意對典型問題從多個角度進行思考，既發散了思維，又培養了能力，而且還構建了重點知識體系，何樂而不為呢？

（作者單位：河北省唐山市豐潤區任各莊鎮中學）