坐標(biāo)系與參數(shù)方程的命題特點及解法

寧夏 張 興 李雪琴

坐標(biāo)系與參數(shù)方程的命題特點及解法

寧夏 張 興 李雪琴

坐標(biāo)法思想是近代數(shù)學(xué)發(fā)展的開端，坐標(biāo)系是用代數(shù)方法處理幾何問題的基本工具．參數(shù)方程是以參變量為中介表示曲線方程的又一種形式，是解決曲線方程的一種思路和方式，所以坐標(biāo)系與參數(shù)方程的學(xué)習(xí)，是提高學(xué)生解決數(shù)學(xué)問題能力，提升學(xué)生綜合數(shù)學(xué)素養(yǎng)的重要途徑，因此成為高考數(shù)學(xué)的必考內(nèi)容，下面就該部分高考試題的命題特點及其解答方法進(jìn)行探究．

一、高考試題的命題特點

從2007年到2016年新課標(biāo)高考共15套數(shù)學(xué)試題，其中關(guān)于極坐標(biāo)與參數(shù)方程的有15道考題．它們的相同之處都涉及坐標(biāo)變換，即直角坐標(biāo)系方程、極坐標(biāo)方程、參數(shù)方程之間的互相轉(zhuǎn)化．它們的不同之處，按已知曲線化分：第一類，直線和圓位置關(guān)系的有10道．其中包括直線和圓相離時的點線距離問題，直線和圓相交時的弦長問題，直線和圓相切時的切點問題．第二類，直線與橢圓共2道．第三類，圓及橢圓位置關(guān)系共3道．從統(tǒng)計數(shù)字上看以直線和圓位置關(guān)系為主．按所求問題劃分：第一類，有關(guān)交點坐標(biāo)、線段長度和圖形面積，共5道．第二類，有關(guān)距離、范圍或最值問題，共8道．第三類，有關(guān)點的軌跡、曲線方程，共2道．從統(tǒng)計數(shù)字上看以有關(guān)距離、范圍或最值計算問題為主．

二、高考試題的題型解析

高考試題按解答方法劃分：第一類，極坐標(biāo)中的運算．第二類，參數(shù)方程中任意點或動點問題．第三類，直線與圓錐曲線相交問題．第四類，點的坐標(biāo)、線段長度、圖形面積、軌跡方程等的計算．

1．極坐標(biāo)中的運算

【例1】（2015·新課標(biāo)Ⅰ理·23）直角坐標(biāo)系xOy中，直線C1：x＝－2，圓C2：（x－1）2＋（y－2）2＝1，以坐標(biāo)原點為極點，x軸的正半軸為極軸建立極坐標(biāo)系．

（1）求C1、C2的極坐標(biāo)方程．

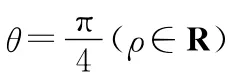
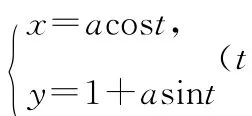
（1）說明C1是何種曲線，并將C1的方程化為極坐標(biāo)方程；

（2）直線C3的極坐標(biāo)方程為θ＝θ0，其中θ0滿足tanθ0＝2，若曲線C1與C2的公共點都在C3上，求a．

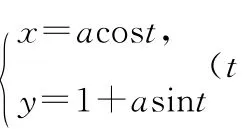
【評析】上面例1、例2的第一問均為極坐標(biāo)與直角坐標(biāo)的互相轉(zhuǎn)化．解答這個問題時需要注意：（1）將點的直角坐標(biāo)（x，y）化為極坐標(biāo)（ρ，θ）時，運用公式，tanθ＝．在［0，2π）范圍內(nèi)，由）求θ時，要根據(jù)直角坐標(biāo)的符號特征判斷出點所在的象限．如果允許θ∈R，再根據(jù)終邊相同的角的意義，表示為θ＋2kπ（k∈Z）即可．（2）將極坐標(biāo)點（ρ，θ）化為直角坐標(biāo)點（x，y），直接運用公式x＝ρcosθ，y＝ρsinθ計算．（3）直角坐標(biāo)方程化為極坐標(biāo)方程時，直接運用公式x＝ρcosθ，y＝ρsinθ代換并化簡．（4）極坐標(biāo)與直角坐標(biāo)的互化，常用方法有代入法、平方法等，還經(jīng)常會用到同乘（或除以）ρ等技巧．第二問為極坐標(biāo)系中的有關(guān)運算．解答方法一結(jié)合圖像進(jìn)行計算，如例1．解答方法二化為直角坐標(biāo)再運算，如例2．

2．任意點或動點用參數(shù)方程

（1）化C1，C2為普通方程，并說明它們分別表示什么曲線；

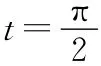
【解析】（1）消去參數(shù)，已知方程可化為：

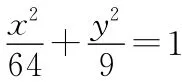
其中C1為圓心是（－4，3），半徑是1的圓．

C2為中心是坐標(biāo)原點，焦點在x軸上，長半軸長是8，短半軸長是3的橢圓．

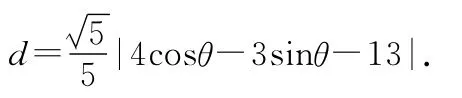
【評析】上面例3的第一問為參數(shù)方程化為普通方程．解答這類題需注意：（1）要注意防止變量x和y取值范圍的擴(kuò)大或縮小，必須根據(jù)參數(shù)的取值范圍，確定x和y的取值范圍．（2）消去參數(shù)通常有代入消元法、加減消元法、平方消元法、乘除消元法和三角消元法等．第二問為求最值或取值范圍．解答這類題需要把曲線方程化為參數(shù)形式，以參數(shù)方程形式表示點的坐標(biāo)，既可以減少約束條件而簡化運算，又能利用特殊的三角變換進(jìn)行計算．

3．直線與圓錐曲線相交問題

【例4】（2016·新課標(biāo)Ⅱ理·23）在直線坐標(biāo)系xOy中，圓C的方程為（x＋6）2＋y2＝25．

（1）以坐標(biāo)原點為極點，x軸正半軸為極軸建立極坐標(biāo)系，求C的極坐標(biāo)方程；

【解析】（1）化簡、整理圓的方程得x2＋y2＋12＋11＝0，

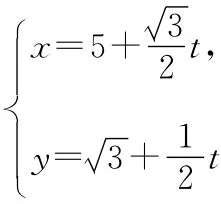
【解析】（1）ρ＝2cosθ等價于ρ2＝2ρcosθ．①

將ρ2＝x2＋y2，ρcosθ＝x代入①，

即得曲線C的直角坐標(biāo)方程為x2＋y2－2x＝0．②

則由參數(shù)t的幾何意義即知，｜MA｜·｜MB｜＝｜t1t2｜＝18．

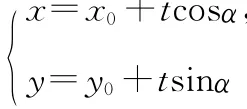
4．求點坐標(biāo)、線段長度、圖形面積、軌跡方程等的計算．

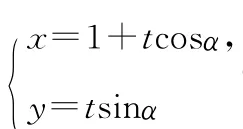
（2）過坐標(biāo)原點O做C1的垂線，垂足為A，P為OA中點，當(dāng)α變化時，求P點的軌跡的參數(shù)方程，并指出它是什么曲線．

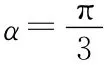
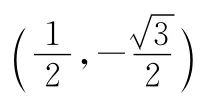
（2）C1的普通方程為xsinα－ycosα－sinα＝0．A點坐標(biāo)為（sin2α－cosαsinα），

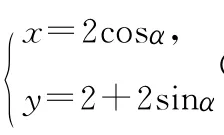
（α為參數(shù)）M是C1上的動點，P點滿足，P點的軌跡為曲線C2．

（1）求C2的方程；

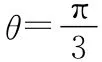
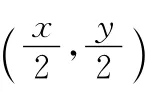
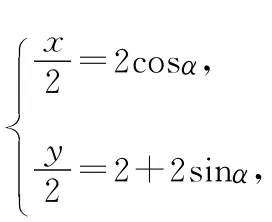
（2）曲線C1的極坐標(biāo)方程為ρ＝4sinθ，曲線C2的極坐標(biāo)方程為ρ＝8sinθ．

【評析】上面例6為求點的坐標(biāo)和軌跡方程，例7為求線段長度和軌跡方程．2015年新課標(biāo)Ⅰ卷23題為求面積．這類問題雖然差別很大，但其解答的基本方法依然是幾種坐標(biāo)的互化，再結(jié)合圖象進(jìn)行計算．

綜上所述，坐標(biāo)系與參數(shù)方程的命題，以直線與圓的位置關(guān)系為主，突出極坐標(biāo)方程、直角坐標(biāo)非常和參數(shù)方程的轉(zhuǎn)化，呈現(xiàn)為四大趨勢，即極坐標(biāo)中的運算，參數(shù)方程中任意點或動點問題，直線與圓錐曲線相交問題，交點坐標(biāo)、線段長度、圖形面積、軌跡方程等基本數(shù)學(xué)問題．通過解題理解坐標(biāo)系的作用，掌握幾種坐標(biāo)方程的轉(zhuǎn)化，提高數(shù)學(xué)應(yīng)用意識和解決問題的能力．體現(xiàn)數(shù)學(xué)的科學(xué)價值、應(yīng)用價值和文化價值，更重要的是提升學(xué)生的綜合數(shù)學(xué)素養(yǎng)．

（作者單位：寧夏回族自治區(qū)固原市第二中學(xué)，寧夏回族自治區(qū)固原市回民中學(xué)）