“奔馳定理”巧解一類三角形的面積比

四川 蔣 敏

“奔馳定理”巧解一類三角形的面積比

四川 蔣 敏

向量既有代數的運算，又有幾何的特征，是溝通幾何與代數的橋梁．當向量遇上三角形，由向量關系得出三角形面積的比值，屬于選擇、填空題中的難題．在高考、自主招生考試中時有出現，其基本特征是：已知三角形內任意一點O，再給出相關向量的線性關系，求相關三角形面積的比值．下面通過一道例題來探求這類題型的相關規律：

【典例】已知點O為△ABC內一點，且有，記△ABC，△BOC，△AOC的面積分別為S1，S2， S3，則S1∶S2∶S3等于 （ ）

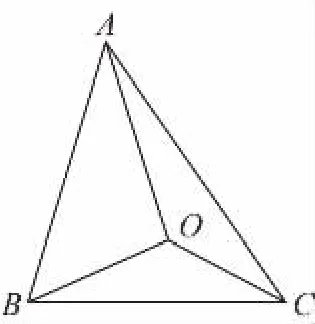
A．3∶2∶1 B．3∶1∶2

C．6∶1∶2 D．6∶2∶1

1．“大膽猜想”——感性思維的直觀解法

【解法1】因為，由直覺并聯想杠桿原理，在質點系下，的1倍與△BOC的面積平衡的2倍才能與△AOC的面積平衡，的3倍才能與△AOB的面積平衡，所以S△BOC∶S△AOC∶S△AOB＝1∶2∶3．

從而△ABC，△BOC，△AOC的面積S1∶S2∶S3＝6∶1∶2，故選C．

【評注】根據題干的已知條件及圖形的大致特征，大膽開啟“猜想模式”，是解答選填題“不擇手段，小題小做”的一種途徑．

2．“小心求證”——理性思維的嚴格推理

攻略1：合理轉化，利用向量共線定理

【解法2】如圖分別取AC、BC的中點D、E，

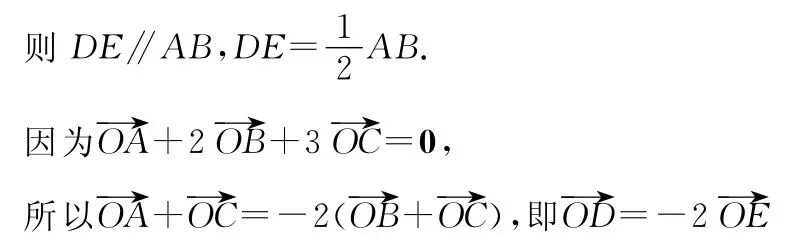
由向量共線定理可知，O，D，E三點共線，

【評注】由于同底的兩個三角形面積之比等于高的比值，利用向量共線定理，找出對應線段的比例，轉化到對應高的比值上來，合理化歸是一種常用的數學思想．

攻略2：利用三點共線的向量表達式

【解法3】如圖，延長AO交BC于M．

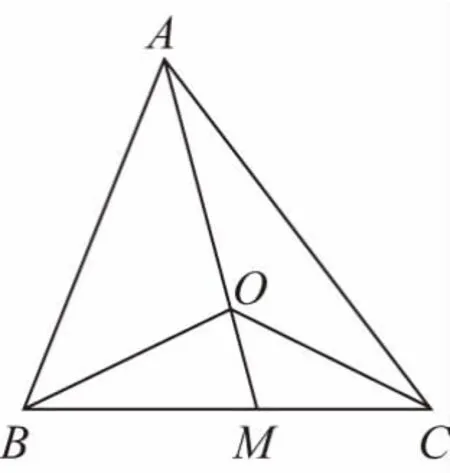
【評注】利用三點共線的向量表達式：起點相同，終點共線，則分解后的系數之和等于1的小結論，巧妙得出λ，步步為營，進一步求得面積的比值，這與解法2有異曲同工之妙！

攻略3：“另辟蹊徑”——解析法閃亮登場

【解法4】如圖，以B為原點，BC所在直線為x軸，建立平面直角坐標系．

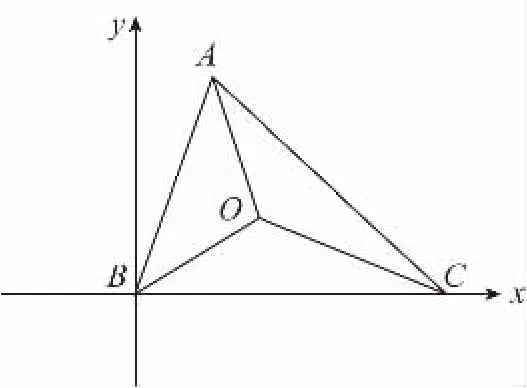
于是△ABC、△BOC面積的比值，轉化為A、O縱坐標的比值，設A、O的縱坐標分別為y1、y2，由于可知等式左邊向量的縱坐標為0：

（y1－y2）＋2（0－y2）＋3（0－y2）＝0，

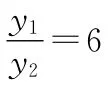
【評注】解析法是將幾何問題代數化，通過坐標運算，體現了數形結合的思想．是解決向量問題的一種常用辦法．選好原點，建好坐標系，過程優美簡潔，一氣呵成！

3．“千呼萬喚始出來”——公式法速解巧解面積比

【定理】已知O為△ABC內的一點，且有，記△BOC，△AOC，△AOB的面積分別為S1，S2，S3，則S1∶S2∶S3＝x∶y∶z．

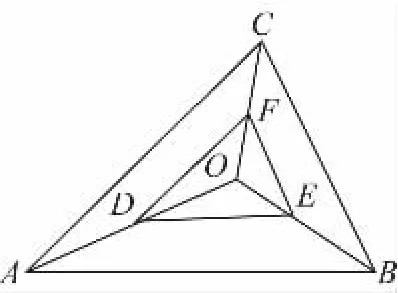
【證明】設．由題意可得，

所以O為△DEF的重心，由重心與頂點形成的三個三角形面積相等，可得S△OEF∶SΔOFD∶S△ODE＝1∶1∶1，

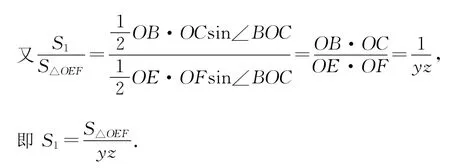
【評注】此類問題對應的圖形特別像奔馳汽車的標志，我們形象地稱上述小結論為三角形中的奔馳定理．特別地，當x＝y＝z＝1時，O為△ABC的重心．

【解法5】由于，由結論可得S△BOC∶ S△AOC∶S△AOB＝1∶2∶3，S1∶S2∶S3＝6∶1∶2，故選C．

【評注】“奔馳定理”結論簡潔，易于記憶．目的性很強，快速得出結果．對于解決選擇題、填空題更加獨具優勢，別具一格．

【變式1】已知P是△ABC內一點，則△ABC與△ABP的面積之比為 （ ）

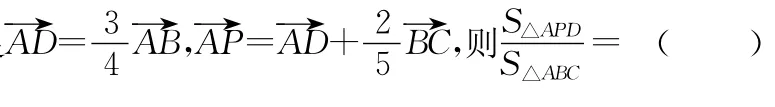
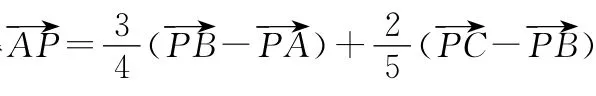
4．“我思考，我快樂”——思維的發散

【推廣1】面積與向量的結合

【例1】（南京大學自主招生考試）已知O為△ABC內的任意一點，求證：．（其中S1，S2， S3為△BOC，△AOC，△AOB的面積）

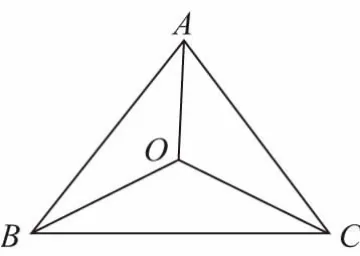
【證明】設∠AOB＝α，∠AOC＝β，OA＝x，OB＝y，OC＝z．利用三角形正弦定理和面積公式，式子左邊

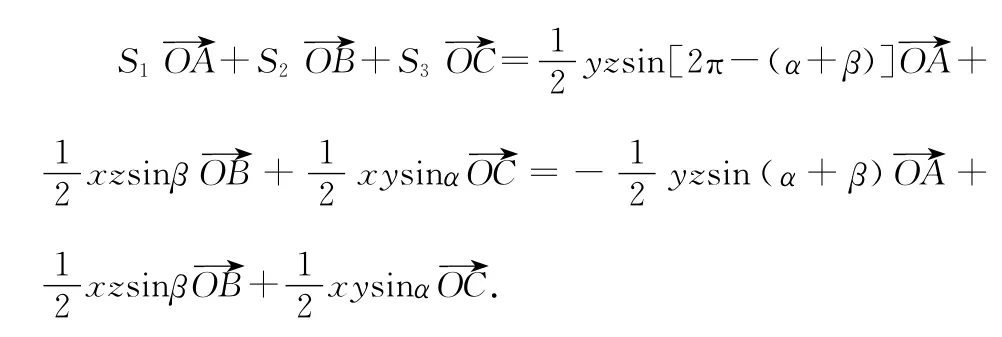
對上式兩邊同時與→OA作數量積得：

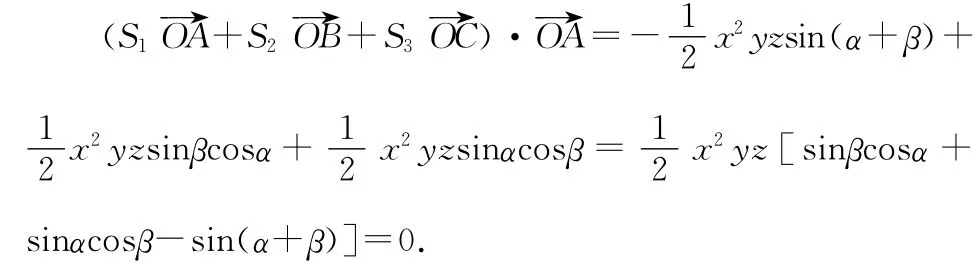
作數量積都得0．

【推廣2】“外面的世界更大”——將三角形內部一點推廣至所在平面內的任意一點

【例2】（全國高中聯賽湖北省預賽）已知點P是△ABC所在平面上的一點，滿足．求△ABP面積與△ABC面積之比．

【解析】將，變形得．

【評注】推廣后的結論中，O為△ABC所在平面內的任意一點，該點可在三角形內部，外部，或者邊上．系數可能出現負數，此時點O在三角形外部，這時，只需取絕對值即可．但必須注意到，此時△ABC的面積不是最大，用結論時的參照系數為實際系數之和．

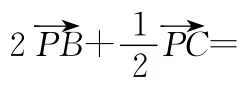
【解析】整理為，由結論可得面積的比為2∶1∶4．

（作者單位：四川省南充龍門中學）