“用樣本的頻率分布估計總體分布”教學設計及反思

郜新利+梁艷娟

教學目標：

1.知識和技能

（1）能列出頻率分布表，能畫出頻率分布的條形圖、直方圖；

（2）會用樣本頻率分布去估計總體分布.

2.過程與方法

（1）體會分布的意義和作用；

（2）初步體會樣本頻率分布和數字特征的隨機性.

3.情感態度與價值觀

（1）體會用樣本估計總體的思想；

（2）通過研究具體問題，體會“探究學習”在學習過程中的作用，使學生體驗成功，增強學習數學的自信心.

重難點分析：

重點：列出頻率分布表，繪制頻率直方圖，用樣本頻率分布去估計總體分布.

難點：統計思維的建立.

教學環節：

復習回顧：某火柴廠生產壁爐火柴、書式火柴、酒店火柴、廣告火柴等系列產品的技術已經成熟，現在要對一批新產品賓館火柴的質量進行檢驗，應該如何操作？

師生互動：教師提問，學生思考討論.

設計意圖：使學生認識到用樣本估計總體的必要性.

本節課我們來共同解決一個問題：

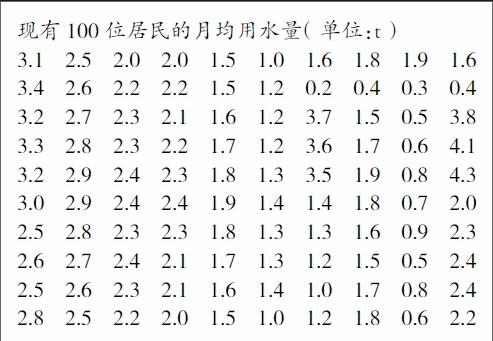
某城市為節約用水，計劃確定一個居民月用水量標準a ，超出a的部分按議價收費.如果希望大部分居民日常生活不受影響，怎樣確定這個標準？需要做哪些工作？

從表中只能看出：最小值是0.2t，最大值是4.3t，其他的在0.2—4.3t之間.

師生互動：教師用幻燈片演示，學生觀察數據特點，并考慮分析數據的基本方法.

設計意圖：用樣本數據分布特征估計總體數據分布.

分析數據的基本方法：

1. 表 （頻率分布表） 2. 圖 （頻率分布直方圖）

畫頻率分布直方圖的一般步驟：

1.求極差：4.3-0.2=4.1，該樣本數據的變化范圍是0.2— 4.3t.

2.定組距：當樣本容量不超過100時，常分成5—12組.取組距為0.5t，則分組數=4.1÷0.5=8.2.因為組數必須取整，因此將數據分為9組.

3.適當分組：為將最小值包含在第一組內，常將第一組區間的左端點適當縮小，[0， 0.5）， [0.5， 1）， [1， 1.5）， … ， （4， 4.5]

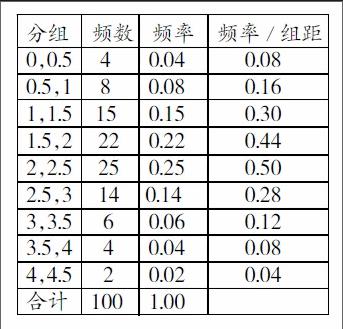
4.列頻率分布表：如下表.

5.畫頻率分布直方圖：如下圖.

師生互動：教師引導，學生討論，動手操作，共同解決問題.

設計意圖：使學生形成規范的畫頻率分布直方圖的步驟.

師：每個小矩形的面積代表什么？

生：各組頻率.

師：所有小矩形面積的和是多少？

生：每個小矩形的面積代表頻率，面積和為1.

師：頻率分布直方圖顯示了樣本數據分布的總體趨勢.圖中最高的小矩形說明什么？

生：說明月均用水量在[2，2.5）內的居民最多.

師：大部分居民的月均用水量都集中在什么區間？

生：在[1，3）之間.

師：居民的月均用水量的分布呈“山峰”狀，而且是“單峰”的.另外還有一定的對稱性.

師：如果當地政府希望使85%以上的居民每月的用水量不超出標準，根據頻率分布表，該如何制定月用水量標準？

生：居民月用水量標準應定為3t.

師：3t的標準一定能保證85%以上的居民每月的用水量不超出標準嗎？

生：不能.頻率分布直方圖具有隨機性.

師：指導學生用圖形計算器畫頻率分布直方圖.

師：怎樣減小誤差？

生：思考并探討.

師：頻率分布直方圖有沒有不足之處？

生：頻率分布直方圖丟失原始數據.

例1：從一種零件中抽取了 80 件，尺寸數據表示如下（單位：cm）：

362.51×1 362.62×2 362.72×2 362.83×3

362.93×3 363.03×3 363.15×5 363.26×6

363.38×8 363.49×9 363.59×9 363.67×7

363.76×6 363.84×4 363.93×3 364.03×3

364.12×2 364.22×2 364.31×1 364.41×1

畫出頻率分布直方圖.

總結頻率分布直方圖的特征：

1.每個矩形面積表示該組頻率.

2.所有矩形面積和為1.

3.若樣本容量為n，分組應在1+3.3lgn.

4.頻率分布直方圖形狀與分組數有關.

5.有隨機性.

6.丟失原始數據.

設計意圖：讓學生學會用圖形計算器輔助學習.使學生體會分組變化對頻率分布直方圖形狀和頻率分布表中數據的影響.體會頻率分布直方圖的隨機性.

練習1：右圖是容量為100的樣本的頻率分布直方圖，

試根據圖中的數據填空：

（1） 樣本數據落在范圍 [ 6，10）內的頻率為 ；

（2） 樣本數據落在范圍[10，14）內的頻數為 ；

（3） 總體在范圍[2，6）內的概率約為 .

設計意圖：讓學生體會頻率分布直方圖的隨機性和

小結：

1.掌握了繪制頻率分布直方圖的步驟；

2.掌握了頻率分布直方圖的特征；

3.學習用樣本估計總體的思想.

作業：教材57頁練習1.

總結：

1.本節課三次使用了圖形計算器，一是新知學習中的作圖；二是新知學習中復雜數據的計算；三是課堂練習.

2.本節課涉及的知識點多，學生動手多，學生參與多.有了圖形計算器的幫助，所有學生都能投入到學習過程中，教師提出的每個問題都在不同程度的學生那里得到了解決，實現了全員參與.本節課教師講解少.教師的作用重在提出問題，引導學生逐步深入地進行學習.

3.本節課的教學效果，用學生的話說：“知識挺簡單的，考試時要是能用計算器就好了.”

教學反思：

當時代的腳步推動我們不斷向前進，當新課程的推行促使我們改進教學理念，當學生的成長要求我們推陳出新的時候，我們已經沒有任何理由拒絕任何新的事物.新事物并不可怕，關鍵是我們能否恰當吸收與運用.圖形計算器本身不是新事物，但新課程與圖形計算器的結合并有效運用仍然是新事物.本節課特點在于探索現代信息技術在數學教學中的應用，發揮圖形計算器處理大量數據的優勢，讓學生的學習更高效，也讓學生體會數學的應用價值.

在學生使用圖形計算器繪制頻率分布直方圖的環節，針對不同的分組情況，如選出有代表性的幾名學生的不同分組方法，畫出不同的頻率分布直方圖可以使學生體會到不同的組距對作圖的影響，更有利于學生體會數據處理的靈活性及科學性.若將題目中的原始數據改為200個，再讓學生體會不同的分組對作圖的影響，課堂效果會更好.

課程中所蘊含的數學的過程學習，對實際問題的處理，數學能力的培養，都要求學生親身參與.本節課的教學可以說為我們提供了一個參考的范例，更好地促進了廣大一線教師對現代信息技術與數學教學相結合的探索.