基于概率模型的攻防效能估算與仿真分析

謝經緯，陳萬春

基于概率模型的攻防效能估算與仿真分析

謝經緯，陳萬春

（北京航空航天大學宇航學院，北京，100191）

建立了一個用于計算彈道導彈突防效能的概率模型，根據導彈攻防對抗中以事件概率、而非以具體結果為指標的評判方式，估算實現突防目的所需要的彈道導彈數量，考慮防御系統的可靠性問題，以及彈頭可能采取的對抗措施。最后通過仿真實驗的方法予以驗證，并對結果進行分析，為實際作戰部署和規劃提供有價值的參考。

概率模型；導彈突防；效能估算；辨識概率

0 引 言

彈道導彈作為一種重要的威懾力自問世以來，引起各國的廣泛關注，因此相應地出現了導彈防御技術。在導彈攻防對抗研究中的一個主要內容就是雙方的作戰目標以及資源上的消耗。20世紀90年代以來，國內外學者對導彈防御系統的效能進行了深入研究：Larson系統地分析了多層次導彈防御體系中的關鍵節點以及優化問題[1]；Wilkening基于概率模型提出以“零突防”為指標的防御效能估算方法[2]；Menq利用Markov鏈優化了多層防御系統的效費比問題[3]；而Kaminer則專注于防御系統各層次之間的相關性[4]；楊曉凌在目標識別、選擇和攔截概率不確定的情況下，研究了攔截彈分配模式的優化問題[5]。

隨著導彈防御技術的不斷發展，彈道導彈的威懾作用受到削弱，因此研究突防策略及其效能十分必要。吳鈺飛在不同的攔截模式下，分階段探討了彈道導彈突防過程中誘餌的影響[6]；吉莉利用伯努利實驗原理，分析了彈道導彈突破多層次防御系統的各種措施，并考慮了誘餌因素[7]；高恩宇建立了目標識別和彈頭突防的概率模型，設計了不同攔截模式下的估算方法[8]。

當前已有的研究成果是事先設定誘餌的識別概率，然后將目標數量作為仿真的輸入，得出一定條件下突防/攔截的概率。相比前者不同的是，本文基于概率模型，以彈頭成功突防作為任務指標，提出進攻方需要投入的彈頭和誘餌的計算方法，針對導彈防御系統的特性與限制，闡明誘餌掩護彈頭的機理，并借助大樣本的仿真對抗予以驗證。

1 對導彈防御系統的設定

由于導彈防御系統的工作流程涉及到探測、識別、跟蹤、發射、攔截、評估等多個環節，并且由雷達/紅外、指揮控制、火力單元、攔截彈等多個子系統組成，復雜程度相當高。為了簡化，引入共模故障的概念，將攔截彈發射前的系統可靠度歸結為一個參數PTrack，表示對一個目標完成探測、識別并持續追蹤的概率[2]。

類似的，將攔截彈的作戰效能也歸結為一個參數k，即單發攔截率（Single-shot Probability of Kill，SSPK），表示從發射、制導到摧毀目標的概率。

本文將防御方的任務指標描述為摧毀所有進攻彈頭的概率P(0)。假設采取集中分配的模式，一次發射I顆攔截彈攻擊所有目標，可以推導出當W個彈頭來襲時，防御系統準確跟蹤并攔截全部彈頭的概率為

對式（1）進行變換，防御系統對攔截彈數量的需求可以寫為[2]

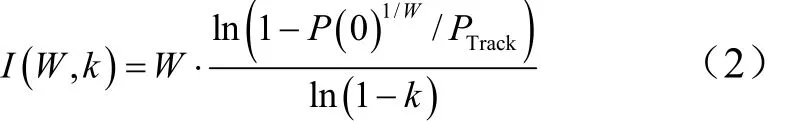
2 進攻彈效能估算

本文僅考慮防御方集中發射攔截彈的模式，突防概率指標設為P(≥1)=1?P(0)，即至少有一顆彈頭突防。根據式（2），可以看出降低P(0)的關鍵點有3處：a）增加進攻彈頭的數量W；b）采用突防措施壓低防御方的跟蹤能力PTrack；c）降低攔截彈的SSPK。

2.1 彈頭不全部被追蹤

如果有足夠的情報，可以掌握防御系統探測、跟蹤、識別目標的總體概率PTrack，或者通過對抗手段將PTrack限制在一定的水平，就可以利用式（2）的內在性質P(0)≤PTWrack，把突防失敗的概率P(0)降低到期望水平。假設PTrack上限為PTrack，并且有：

定義：

只要彈頭的數量達到或超過W時，就能夠以1?P(0)的概率保證至少有1顆彈頭不被跟蹤而直接突防。這相當于飽和攻擊的一種體現。

如果防御方跟蹤目標的能力很高，或者情報不足難以確定其水平，出于保守只好假設PTrack=1，也就是說所有彈頭都會被防御系統準確識別并跟蹤。

2.2 彈頭不全部被攔截

當攔截彈的SSPK較高或者進攻方對突防概率P(≥1)要求苛刻（即容忍的突防失敗的概率P(0)較小）時，可能出現下面的情況：代入防御方所擁有的攔截彈個數I后，

這表明即使W=I時，仍不能滿足要求。然而假設每顆攔截彈只能應對一個目標，則W=I +1是一定能夠突防的，換而言之，防御方需要一個潛在條件是I≥W。這樣就可以分情況來估計所需彈頭的數目：

式中 ()F I無法用解析函數來表示，是W滿足式（2）在TrackP=1情況下的解。這里需要確保W是唯一存在的，證明過程如下[9]：

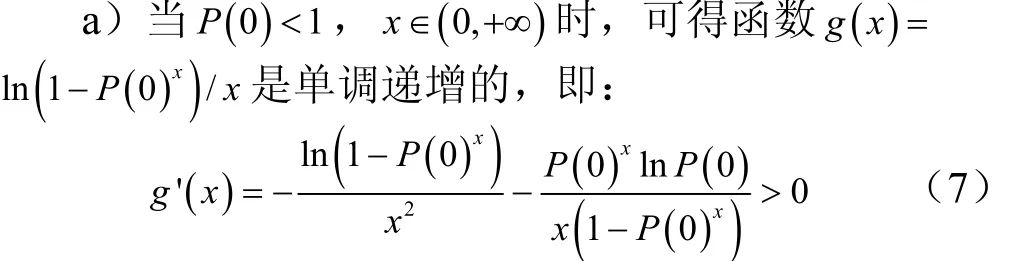
b）當P(0)＜1，滿足g(+∞)=0時，在式（2）的第2種情況下，又有：

由于單調性，則存在唯一解x=1W∈(1I,+∞)，亦即W∈(0,I)，使得：

此時：

也就是式（2）在PTrack=1下的形式。計算W的一種方法就是迭代求近似解，設初值為W0=I，代入下式中：

當滿足條件P(0)＞(1?k)I時，序列{Wi}是收斂到唯一解W的。

3 誘餌效應

防御系統是依靠誘餌和彈頭在信號特征上的區別（如紅外輻射、電磁波等）來辨識目標的。這可以描述為一對信號閾值的上下限，稱作識別區間[a, b]，凡是信號值落在該區間內的目標，就被識別為彈頭，反之則從目標序列中剔除。但實際上，防御系統對彈頭和誘餌的差異所知有限，特別是進攻方有意混淆二者的信號特征時，防御方只好放寬識別區間來確保跟蹤所有的彈頭。由此將不可避免地引入識別率的問題[2]，具體來講，包括：

a）彈頭被正確識別的概率Pww，即彈頭信號處在識別區間內；

b）彈頭被判定為誘餌的概率Pwd，即彈頭信號處在識別區間外；

c）誘餌被正確識別的概率Pdd，即誘餌信號處在識別區間外；

d）誘餌被判定為彈頭的概率Pdw，即誘餌信號處在識別區間內。

彈頭突破防御的方式有2種：a）彈頭被準確識別，但防御系統未能成功攔截；b）彈頭被識別為誘餌，防御系統未予攔截。為了使Pwd盡可能小，防御系統需要將識別區間放寬，因此容易把誘餌識別為彈頭（即Pdw增大），也就是說Pww和Pdw是正相關的。

3.1 誘餌辨識概率

圖2為識別區間與目標識別區的關系，展示了依靠識別區間來辨別彈頭和誘餌的情形。

圖2 識別區間與目標辨識概率

如果防御系統不希望遺漏掉彈頭，則至少需要保證Pww≥PTrack，為此可能被迫將識別區間[a, b]設置得較寬。對于進攻方而言這一區間是未知的，假設防御方按μw對稱設置為[μw?Δ,μw+Δ]，也就是式（11）中定積分的上下限。這是識別概率Pww不降低的情況下，區間長度b?a最小的情形。下面重寫式（12）為標準正態分布，即構造中間變量t∈N(0,1)，有：

根據所需的Pww值查詢標準正態分布表，將Δ代入誘餌信號服從的正態分布xd∈N()，從而獲得相應的Pdw，即防御系統把誘餌識別為彈頭的概率：

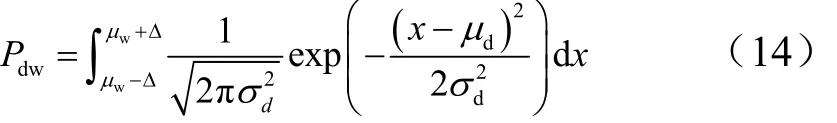
3.2 估算誘餌的數量

進攻方通過增加誘餌的數量D，來消耗防御系統的探測以及攔截能力。從統計學的意義上來講[2]，此時被防御方認作“彈頭”的目標個數W*可以寫作：

仍然假設防御方對W*個“彈頭”平均分配了n顆攔截彈，根據式（1），為了達成防御概率P(0)，對n有如下要求：

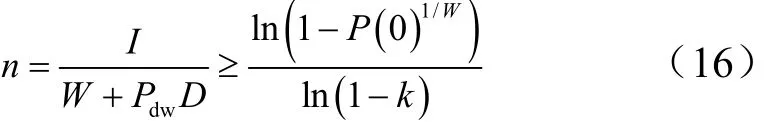
其中，不等號右端的含義是出于防御方的需要，只關注W個真實彈頭的攔截結果，不關注誘餌與攔截彈的交戰情況。因為誘餌的作用是在攔截彈總數I較大的情況下，稀釋掉分配給每個目標的攔截彈數量n，直至式（16）反號。需要的誘餌數量為

4 攻防仿真與分析

根據前面建立的關于彈頭和誘餌數量的估算模型，利用大氣層外攔截彈仿真程序軟件來設計仿真實驗[11,12]，其運作流程如圖3所示。

在誘餌方面，包括電子假目標和紅外誘餌兩種，前者針對預警雷達，誘使防御系統發彈攻擊。當外大氣層攔截器（Exo-atmospheric Kill Vehicle，EKV）分離并開啟紅外導引頭后，會辨識出電子假目標，因此只有部分EKV追蹤的是真實彈頭；紅外誘餌對預警雷達不起作用，針對的是攔截彈的EKV，以一定的概率誘使導引頭選擇追蹤自己，從而掩護彈頭突防。

圖3 攔截仿真流程

4.1 彈頭突防效能

由于第2章中不同情形下彈頭的估算方法有所差異，所以針對彈頭仿真設計了2種情況，分別予以驗證。圖4為估算結果與仿真結果對比。

圖4 估算結果與仿真結果對比

a）第1部分仿真條件設置如下：1）防御系統跟蹤目標的概率PTrack=0.999；2）攔截彈對目標的SSPK設為k=0.7；3）攔截彈總數I=1 200；4）要求突防概率P(≥1)=10%，11%，…，90%。

首先估算彈頭數量。從進攻方的角度考慮，在估算中認為PTrack=1，因此通過式（10）迭代得到的彈頭數量會多于實際值。由于PTrack=0.999，多數情況下彈頭數量的需求取決于防御方的攔截能力，而非探測能力。只有任務指標P(≥1)低于18%時（見圖4中拐點處），由式（4）估算出來的彈頭數量才會低于式（11）。

作為對比，將P(0)=1?P(≥1)代入式（2）解出準確的彈頭數量W，并輸入仿真軟件得到突防概率（見表1）。

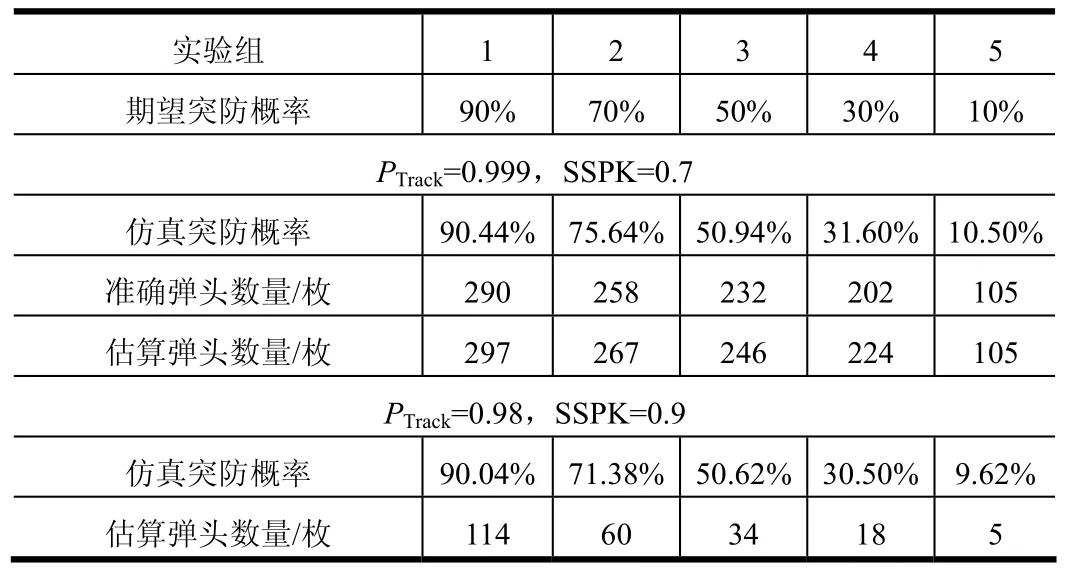
表1 彈頭的部分仿真結果

b）第2種情形：1）防御系統跟蹤目標的概率PTrack=0.98；2）攔截彈對目標的SSPK設為k=0.9。

跟蹤目標的概率PTrack降低了，因此將由式（4）來估算進攻彈頭的數量。值得注意的是，通過反解式（2）已經無法得出有效的彈頭數量（結果均為復數），原因是當PTrack＜1時不保證適用于式（6）及后續證明。實際上由防御系統跟蹤目標的概率決定了突防效果。

由圖4可知，第1種情形下對彈頭數量的估算值明顯高于準確值W；而第2種情形下，相同的突防概率需求的彈頭數量大幅減少，實際上都來自PTrack的影響。說明準確掌握防御系統的PTrack值十分關鍵。

4.2 誘餌配合彈頭突防

假設防御系統追蹤目標的能力足夠強，為了提高彈頭的突防概率，需要采用誘餌來分散防御系統的攻擊。從4.1節第1部分的仿真結果來看，即使投入105枚彈頭，突防概率也僅有10%左右。進一步限制W≤50，仿真條件設置如下：

a）防御系統跟蹤目標的概率PTrack=0.999；

b）攔截彈對目標的SSPK設為k=0.7；

c）攔截彈總數I=1 200枚。

假設彈頭的信號符合標準正態分布N(0,1)，根據式（13），為了確保Pww≥PTrack，有Δ/ σw=3.30，說明防御系統識別區間至少包含[-3.30，3.30]。那么每次當誘餌信號也進入該區間，就會被防御系統識別為彈頭。

假設電子誘餌信號特征符合正態分布N(1,1)，紅外誘餌符合N(?1,1)，均比彈頭信號偏離一倍標準差。令Dj表示雷達誘餌數量，Db表示紅外誘餌數量。根據2種誘餌在不同階段的作用機理，得到：

從式（18）來看，雷達誘餌（指數項）分散了針對每個目標的攔截彈數量，與式（16）左端的含義一致；對于紅外誘餌的影響，根據條件概率定義[10]，攔截彈需要先按概率在W+PdwDb個目標里選中彈頭，再乘以摧毀彈頭的概率k。所以，從形式上可以認為是紅外誘餌降低了攔截彈的SSPK。加入誘餌后的仿真結果如表2所示。

表2 加入誘餌的仿真結果

對比4.1節，彈頭雖然減少卻取得了更好的突防效果，原因分析如下：假設防御系統跟蹤能力只受電子誘餌影響，將μw=0，Δ=3.30代入式（14），對電子誘餌的誤判率為Pdw≈0.989，表明誘餌幾乎全部辨識錯誤。如果想要避免這樣的結果，勢必縮小識別區間，盡可能不將誘餌納入，例如[-2，2]，且不論此時仍有Pdw≈0.84，關鍵是代入式（12）后Pww＜0.96，則有PTrack＜0.96，根據式（1）當W=50時算出P(0)≈0.13，即突防概率P(≥1)≈0.87。

可以說，誘餌令防御系統的效能大幅度下滑，且無論識別區間如何選取。提示了進攻方一方面要讓μd與wμ接近，使得誘餌盡量擬真；另一方面，可以擴大彈頭的特征樣本散布，即標準差wσ，使得彈頭之間互有差異，或者多種彈頭混合突防。利用wwP與dwP之間的正相關性來確保突防概率。

5 結束語

經過對導彈攻防對抗的原理和各個環節的分析，本文建立起了基于概率分布的估算模型，以彈頭突防概率為指標，結合防御系統的探測、跟蹤、可靠性因素，以及目標的識別概率問題，提供了進攻彈和誘餌的數量估算方法。從進攻方的角度來看，除了攔截彈SSPK和數量的因素外，還要考慮防御系統的TrackP和誘餌的dwP可能為彈頭突防所帶來的貢獻。最后通過仿真的方法予以檢驗，并且分析了估算與仿真的結果，印證了關于彈頭、誘餌數量和防御系統內部因素對攔截概率的影響。未來進一步工作可以拓展到不同的攔截彈發射模式，以及多層防御系統效能分析。

[1] Larson E V, Kent G A. A new methodology for assessing multilayer missile defense options [M]. California: RAND, 1994.

[2] Wilkening D A.. A simple model for calculating ballistic missile defense effectiveness [J]. Science & Global Security, 1999, 8(2): 183-215.

[3] Menq J Y, Tuan P C, Liu T S. Discrete Markov ballistic missile defense system modeling[J]. European Journal of Operational Research, 2007, 178(2): 560-578.

[4] Kaminer B Ι, Ben J Z. A methodology for estimating and optimizing effectiveness of non-independent layered defense[J]. Systems Engineering, 2009, 13(2): 119-129.

[5] 楊曉凌, 邱滌珊. 三種不確定性條件下的攔截器目標分配模型[J]. 彈箭與制導學報, 2012, 32(4): 4-8.

[6] 吳鈺飛, 羅小明, 申之明, 賀平. 誘餌影響下多枚彈道導彈突防效能研究[J]. 裝備學院學報, 2008, 19(3): 57-62.

[7] 吉莉, 陳磊. 基于概率模型的彈道導彈突防措施分析[J]. 火力與指揮控制, 2009, 34(11): 98-101.

[8] 高恩宇, 劉曉坤. 彈道導彈防御系統攔截概率的簡化模型[J]. 導彈與航天運載技術, 2013(3): 35-38.

[9] 周民強. 數學分析（第一冊）[M]. 上海: 上海科學技術出版社, 2002. [10] 何書元. 概率論與數理統計[M]. 北京: 高等教育出版社, 2006.

[11] 劉芳, 陳萬春. PAC-3攔截彈六自由度反導建模與攔截仿真分析 [J].飛行力學, 2012, 30(5): 440-443.

[12] 郭筱曦. 標準-3導彈武器系統建模與攻防對抗仿真[D]. 哈爾濱: 哈爾濱工業大學, 2011.

Estimation and Simulation Analysis Based on Probabilistic Model for the Effectiveness of Penetration and Defense

Xie Jing-wei, Chen Wan-chun
(School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing, 100191)

A probabilistic model for calculating ballistic missile penetration effectiveness is developed. The objective for judgment is stated as a probability of events during the engagement, not a specific result. Based on this point, the reliability of defense system, and counter-measures that may be used by ballistic missiles is taken into account. Estimation of the amount of ballistic missiles is made to achieve the objective of penetration. At the end of paper, simulation experiments are presented to examine the model. And analyses for simulation results were given which might be available for missile deployment and programming.

Probabilistic model; Ballistic missile penetration; Effectiveness estimation; Probability of identification

TJ76

A

1004-7182(2017)04-0001-05 DOΙ：10.7654/j.issn.1004-7182.20170401