自適應全程滑模變結構在軌跡跟蹤上的應用
王子瑜,李 君,王海濤,宋敬群
自適應全程滑模變結構在軌跡跟蹤上的應用
王子瑜,李 君,王海濤,宋敬群
(北京宇航系統工程研究所,北京,100076)
針對高超聲速飛行器(hypersonic reentry vehicle, HRV)軌跡跟蹤問題,提出一種自適應全程滑模變結構軌跡跟蹤方法。首先,基于最優化理論設計全程滑模面,使系統的軌線一開始便落在切換面上;其次,采用滑模變結構控制與自適應控制相結合的方法,根據辨識結果自動調整控制律,在保證穩定性的同時削弱抖振;最后,采用Lyapunov定理證明系統的穩定性,并在一定的干擾作用下,將所設計的跟蹤算法進行數值仿真,通過與二次型調節器(linear quadratic regulator,LQR)跟蹤算法進行比較,驗證了控制器的有效性。
高超聲速飛行器;全程滑模變結構控制;自適應控制;最優化理論
0 引 言
臨近空間飛行器具有飛行速度快、飛行空域廣、響應時間快的特點,不但突防能力強,而且能夠實現快速機動部署,易于適應戰場形勢變化需要,近年來備受各國關注[1],但是飛行器的氣動特性和大氣環境隨著飛行狀態的變化將發生較大的變化[2],成為跟蹤控制系統設計面臨的重要問題。再入制導分為兩個部分:縱向標準軌跡的設計和軌跡跟蹤。Harpold在阻力加速度-速度平面設計了一個用于航天飛機的跟蹤制導律,通過僅調整傾側角完成了對標準軌跡的跟蹤[3],成為再入制導發展史上的一個里程碑。
為了進一步提高系統的自主、自適應以及魯棒性,很多學者在軌跡跟蹤方面做了大量的研究。Dukeman利用線性二次型調節器(Linear Quadratic Regulator, LQR)設計了一個時變的反饋跟蹤控制器,通過同時調整攻角與傾側角在不同的初始條件下完成了對高度、速度和彈道傾角的同時跟蹤[4]。但是這種方法一方面對精確數學模型依賴性大,另一方面當氣動參數等發生較大變化時,魯棒性較差。
滑模變結構控制(Sliding Mode Control,SMC)由于具有動態品質好、控制精度高、魯棒性強、干擾抑制能力強的優點,成為一種控制不確定系統的有效方法[5]。從20世紀50年代蘇聯學者Emelyanov提出變結構控制方案起[6],滑模變結構以其獨特的優點,廣泛應用于機器人、工業控制、航空航天等控制領域[7,8]。但是,控制系統對不確定性的魯棒性僅體現在滑動模態階段,而系統在處于趨近模態階段時,對系統參數攝動和外界干擾較為靈敏,同時變結構帶來的抖振現象成為滑模變結構控制理論研究的重要內容。
因此,為了更好地提高系統魯棒性,本文采用自適應全程滑模變結構控制方法進行跟蹤制導,在變結構控制律中引入時變因子項,優化了滑模面的設計,消除了趨近階段,使系統從初始狀態到平衡點具有全過程魯棒性。在此基礎上,結合自適應方法對系統不確定性進行估計,大大減小了變結構的抖振現象。
1 滑動模態運動方程
考慮地球為不旋轉圓球時,高超聲速飛行器在航跡坐標系中相關無動力滑翔的無量綱質心運動方程為[9]
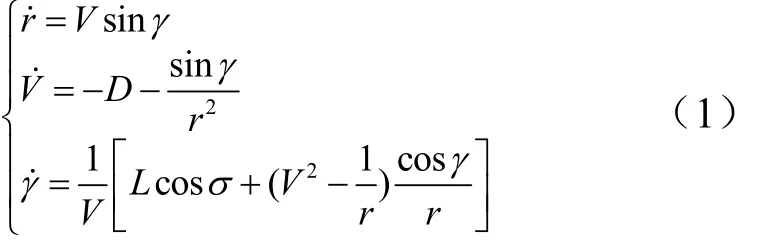
式中 r為地心距,無量綱化因子為地球半徑R0=6 378 km;V為地球相對速度,無量綱化因子為側角;L,D分別為升力加速度和阻力加速度,L=ρ(VcV)2SrefCL/(2mg0),D=ρ(VcV)2SrefCD/(2mg0),均為控制變量攻角α的函數,其中,ρ為大氣密度,Sref為高超聲速飛行器參考面積,m為高超聲速飛行器的質量,CL,CD分別為升力系數和阻力系數。
整個滑翔階段的標準軌跡用r*,V*和γ*表示,名義控制量攻角、傾側角用α*和σ*表示,本文的目的就是設計一個具有魯棒性的軌跡跟蹤控制器,通過同時調整攻角與傾側角,在氣動參數發生大范圍攝動的情況下完成對標準軌跡的跟蹤。
定義x=[r Vγ]T?[r*V*γ*]T∈R3為狀態偏差,(1)進行小擾動線性化,有:

式中
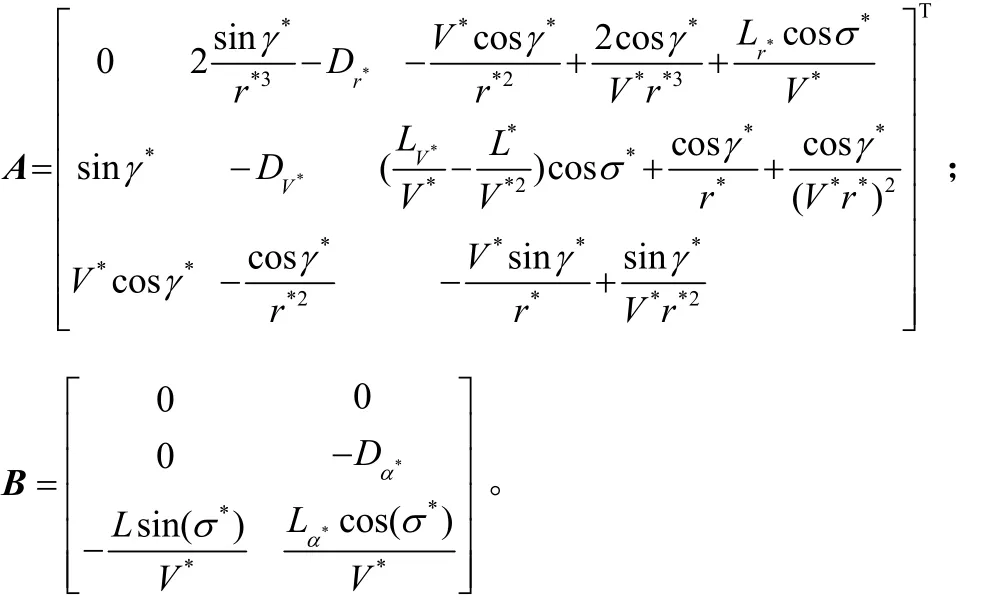
為升、阻力加速度對r,V,α的偏導數。最終縱向軌跡跟蹤控制變量為

式(3)中的σ符號由類似航天飛機的橫向制導方法決定,即設置隨速度變化的航向角誤差走廊,當航向角誤差達到走廊邊界時進行傾側角符號的反向,使航向角誤差有所減小。
2 控制器設計
2.1 系統描述
考慮下列非線性不確定被控系統:
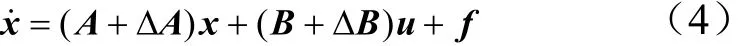
式中 x(t)∈R3為狀態變量;u(t)∈R2為控制變量,ΔA∈R3×3,ΔB∈R3×2為參數攝動矩陣;f為外界干擾及模型誤差。
對于此系統作如下假設:
假設1:ΔA( x,t),ΔB( x,t)均為Lebesgue可測,對任意時間連續有界,ΔA˙( x,t),ΔB˙( x,t)一致有界。
假設2:存在矩陣A′,B′,f′使得ΔA=BA′,ΔB=BB′,Δf=Bf′。
假設3:存在正常數?a,?b,?f,使得ΔA≤?a,
考慮到A和B形式,式(2)可寫成:
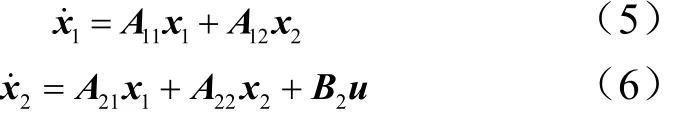
2.2 全程滑模面的設計
為了使系統軌跡一開始就落在滑模面上,因此引入一個隨時間變化的全程滑模因子()tW,設計滑模切換函數為
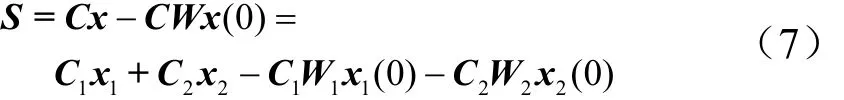
式中 C1,C2為滑模設計參數,保證滑模面上系統狀態穩定,C1>0,C2>0。不失一般性,選擇C2=I2。Re(βi)>0(i =1,2,3)是全程滑動因子,使得系統狀態開始就能處于滑模面上。
2.2.1 滑模參數矩陣C的設計
在滑模面上,將S=0代入式(7)得:則,系統的滑模運動方程為

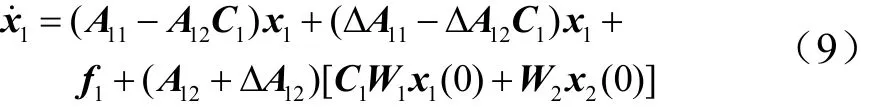
式(9)描述的系統標稱方程為

為了優化滑模面上狀態的動態特性,設計性能指標為
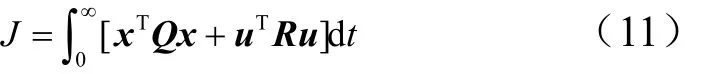
式中 Q為狀態加權矩陣。
由于在滑動模態優化問題中,滑動模的運動與控制量無關,因此取=R0,則式(11)可寫成:
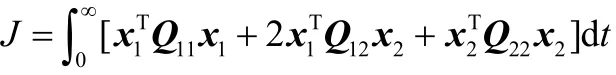
為了將最優滑動模設計問題寫成二次性能指標下的一般形式,引入新的變量:
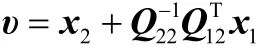
則,性能指標改寫為

相應的標稱滑動模方程為

由最優控制理論,在滑動模方程式(13)中,作為控制作用的向量υ其最優選擇為
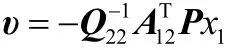
式中 P為下列Riccati方程的唯一解:
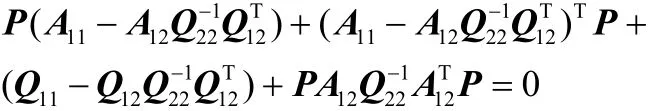
則有:

2.2.2 滑模移動參數iβ的設計
在全程滑模變結構系統中,1x的運動特性由滑模參數矩陣C的設計來保證,而2x的期望運動特性由滑模移動參數iβ來確定。
由式(7)以及=S0,有:
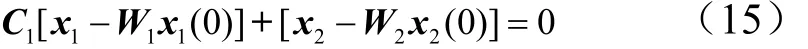
由式(10)可知系統期望的滑動模態運動為
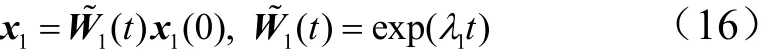
式中 λ1為矩陣(A11?A12C1)的特征值。
結合式(15)、式(16),故而設計:

可以通過選擇合適的2β和3β,使2x按照所期望的運動特性運動。
2.3 全程滑模態結構控制律設計
第2.2節中,滑模面的設計保證了系統在滑模面時具有魯棒性。此節中將設計一個控制律在系統受到外界干擾及由于參數攝動而偏離滑模面時,能夠在有限的時間內重新回到并且可靠地保持在滑模面上。
將假設2代入式(4),有:
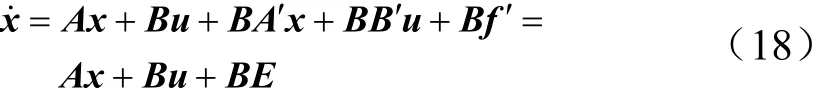
式中 E為系統不確定性總和,E=A′ x+B′ u+f′。
設計自適應全程滑模變結構控制律為
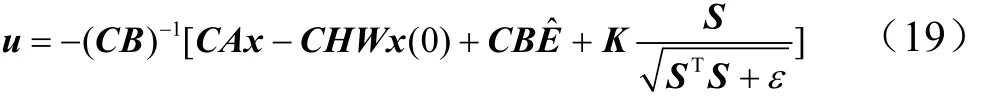
式中 H=diag [?β1?β2?β3];ε為一個很小的正常數;K為常數對角陣;E?為對不確定性總和E的估計,自適應控制律設計為

式中 η=diag[η1η2η3],ηi>0(i=1,2,3)
定理:對于不確定系統式(4)與切換函數式(7),如果滿足假設1至假設3,在控制律式(19)的作用下漸進穩定。
證明:選擇Lyapunov函數,有:
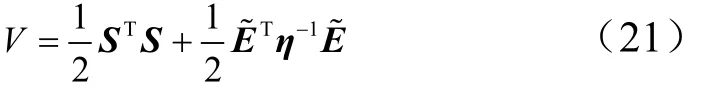
式中 E~=E??E。
由式(7)、式(18)至式(20)得:
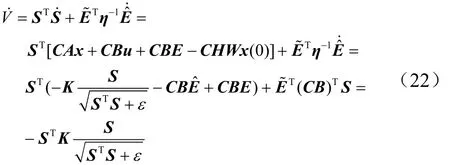
所以,有V˙<0(?S≠0)
由式(22)可見E?能夠收斂到E,S能夠收斂到0。
從S的定義式(7)可以看出,在有限時間內不確定系統的跟蹤誤差x能夠漸近收斂至0。
因此,系統在Lyapunov意義下漸近穩定。
3 仿真分析
為了驗證上述控制方法的有效性,分別利用自適應全程滑模變結構與LQR方法進行仿真,滑翔段射程為5 000 km。
初始以及終端條件為

氣動參數攝動為
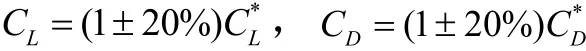
圖1至圖3為在氣動參數攝動時采用自適應全程滑模變結構控制方法的參考軌跡與實際軌跡的對比。從圖中可以看出即使氣動參數存在大范圍的不確定性,實際軌跡仍能較好跟蹤標準軌跡。
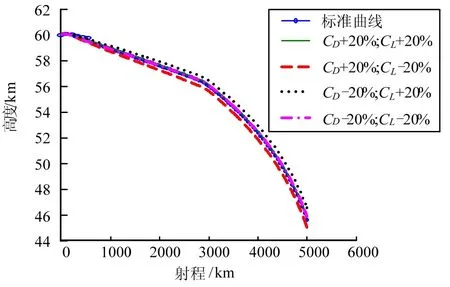
圖1 高度跟蹤曲線
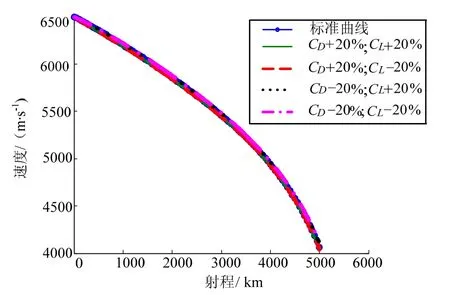
圖2 速度跟蹤曲線
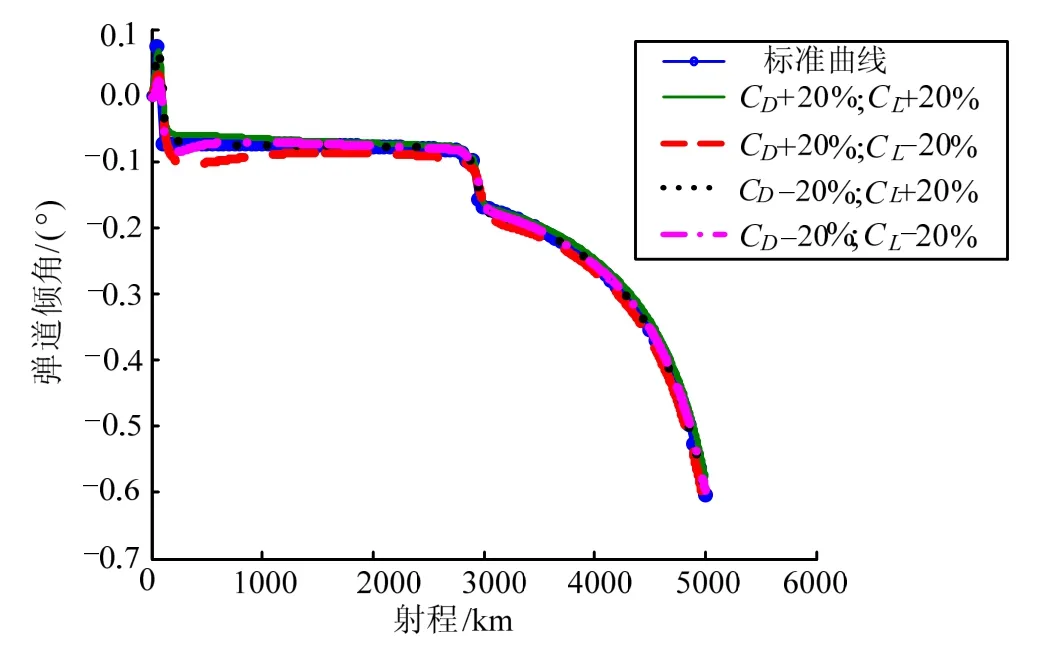
圖3 彈道傾角跟蹤曲線
表1給出了分別采用自適應全程滑模變結構控制方法與LQR控制方法的終端誤差對比。從表中數據可以看出自適應全程滑模變結構控制方法具有更好的跟蹤效果,尤其是在速度狀態的跟蹤方面具有更強的適應能力與魯棒性。
圖4、圖5給出了采用自適應全程滑模變結構控制方法的控制變量曲線,從圖中可以看出采用上述的控制策略使得由變結構帶來的抖振現象大大減小。
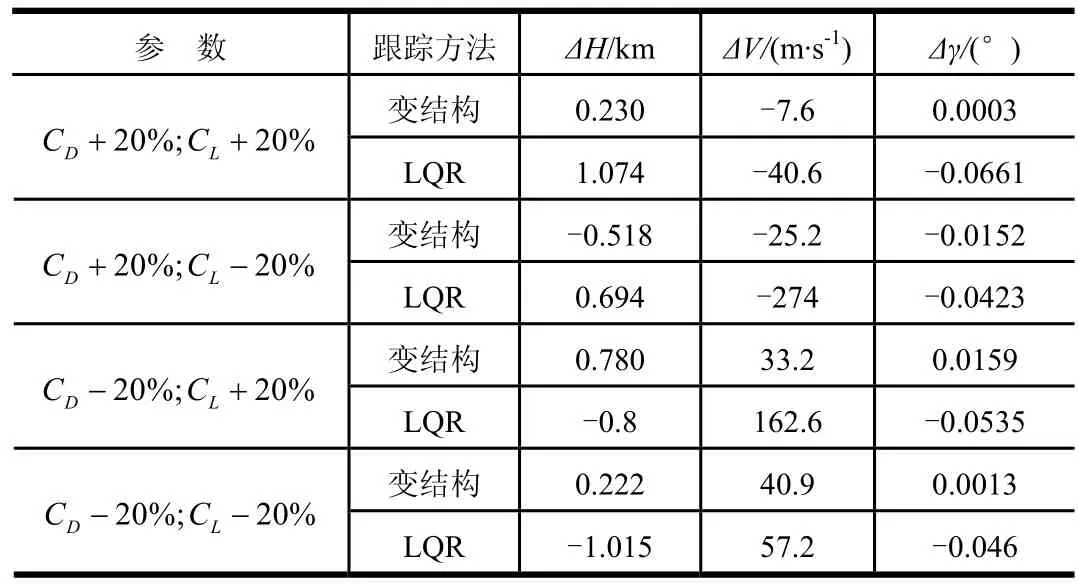
表1 仿真數值結果
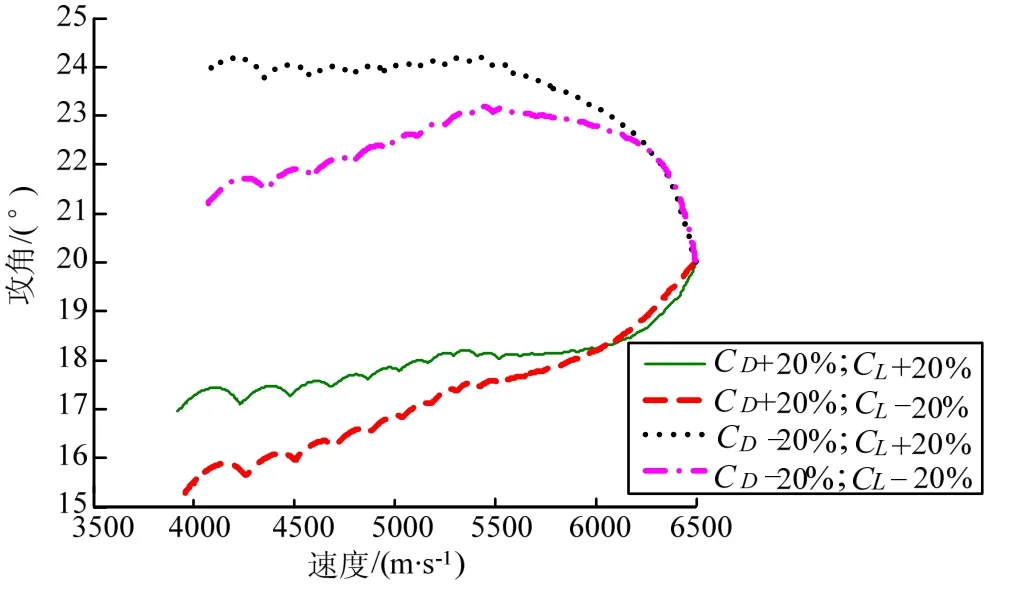
圖4 攻角曲線
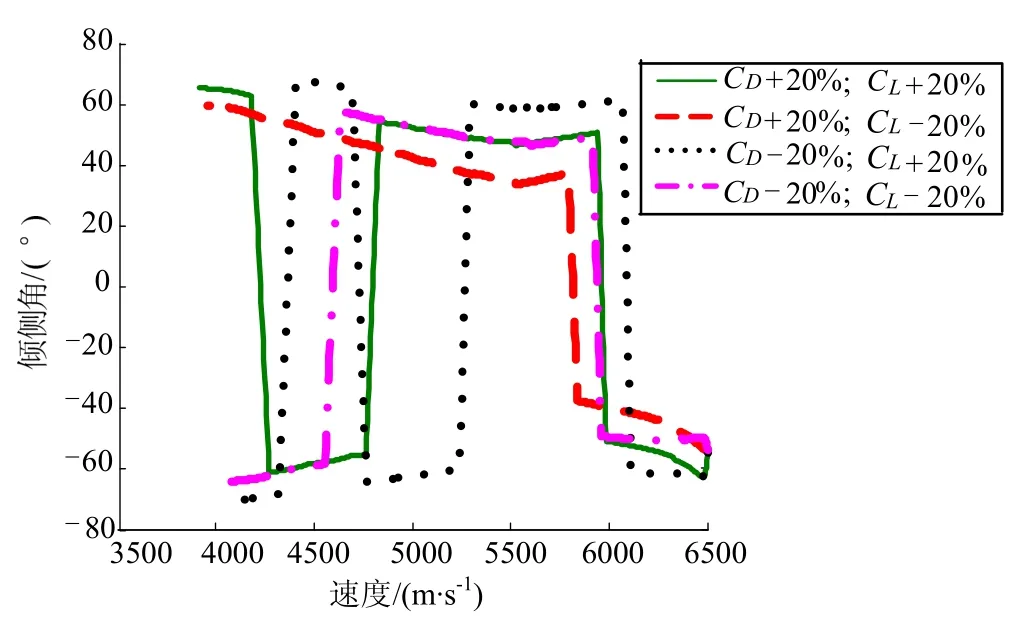
圖5 傾側角曲線
4 結 論
針對滑翔段軌跡跟蹤問題本文提出了一種新型的自適應全程滑模變結構控制方法,采用自適應控制器在線辨識系統的不確定性誤差,有效地減小了系統的抖振現象,在此基礎上,利用Lyapunov穩定性理論證明了在存在參數攝動以及模型不確定性的情況下系統漸近穩定,并通過數值仿真,得到以下結論:a)在存在氣動參數大范圍攝動的情況下,采用自適應全程滑模變結構跟蹤控制方法能較好的跟蹤標準軌跡,與LQR方法相比,跟蹤誤差大大減小,魯棒性大大增強。
b)采用自適應控制理論,系統抖振得到有效減弱,使跟蹤控制器更易于實現。
[1] 張海林, 周林, 等. 臨近空間飛行器發展現狀及軍事應用研究[J]. 飛航導彈, 2014(07): 3-7.
[2] Chaudhary A, Nguyen V, Tran H, Poladian D, Falangas E. Dynamics and stability and control characteristics of the X-37[C]. Montreal: AΙAA Guidance, Navigation, and Control Conference and Exhibit, 2001.
[3] Harpold J C, Graves C A. Shuttle entry guidance[J]. The Journal of the Astronautical Sciences, 1979, 25(3): 239-268.
[4] Dukeman Greg A. Profile following entry guidance using linear quadratic regulator theory[C]. Montreal: AΙAA Guidance, Navigation, and Control Conference and Exhibit, AΙAA 2002.
[5] Young K, Ozguner U. Sliding-mode design for robust linear optimal control[J]. Automatic-Oxford, 1997(33): 1313-1324.
[6] Hung J Y. Gao W, Hung J C. Variable structure control: a survey[J]. ΙEEE Transactions on Ιndustrial Electronics, 1993, 40(1): 2-22.
[7] Jing Y W, Mao Y E. Adaptive global sliding mode control strategy for the vehicle antilock braking systems[C]. St. Louis: American Control Conference, Hyatt Regency Riverfront, 2009.
[8] Li H M, Ye X. Sliding-mode PΙD control of DC-DC converter[C]. Taichung : Ιndustrial Electronics and Applications, 2010 the 5th ΙEEE Conference, 2010.
[9] Shen Z. On-board three-dimensional constrained entry flight trajectory generation[D]. Dissertation Abstracts Ιnternational, The Florida State University, 2002.
Application of Adaptive Global Sliding Mode Control Method in Trajectory Tracking
Wang Zi-yu, Li Jun, Wang Hai-tao, Song Jing-qun
(Beijing Ιnstitute of Astronautical System Engineering, Beijing, 100076)
A trajectory tracking guidance control law is proposed based on the theory of adaptive global sliding mode control, which can help solve the problem of trajectory tracking for HRV. Firstly, a global sliding mode surface is designed based on optimization theory, which guarantees the sliding mode motion of the system lie on the sliding surface at the beginning. Secondly, an adaptive reaching law is incorporated to estimate the system uncertainties, so that the chattering phenomenon is effectively relaxed. Finally, the robustness of the system is proofed by Lyapunov theory. Numerical simulations demonstrated the capability and effectiveness of the proposed method under the condition of aerodynamic data perturbations.
Hypersonic vehicle; Global sliding mode control; Adaptive control; Optimization theory
V448.235
A
1004-7182(2017)04-0059-05
DOΙ:10.7654/j.issn.1004-7182.20170414
2016-09-06;
2016-09-28
王子瑜(1985-),男,工程師,主要研究方向為電氣系統總體設計

