淺埋泥水盾構隧道開挖面被動失穩分析

李鳳濤，唐曉武，劉維, ，趙宇，唐強

?

淺埋泥水盾構隧道開挖面被動失穩分析

李鳳濤1, 2，唐曉武1，劉維1, 3，趙宇4，唐強3

(1. 浙江大學濱海與城市巖土工程研究中心，浙江杭州，310058；2. 中國鐵路設計集團有限公司，天津，300143；3. 蘇州大學城市軌道交通學院，江蘇蘇州，215131；4. 浙江大學防災工程研究所，浙江杭州，310058)

基于杭州沿江運河隧道工程，采用有限差分數值軟件FLAC3D對開挖面被動失穩進行研究。根據數值分析中失穩模式提出局部被動失穩二維機動場模型并采用上限分析法推導開挖面極限支護壓力。對運河隧道工程進行支護壓力上限解分析。研究結果表明：支護壓力過大會引起開挖面局部被動失穩，開挖面局部失穩區域底部至隧道拱頂距離與隧道直徑的比值主要受覆土厚度的影響，土體摩擦角變化對其影響較小。被動失穩引起開挖面前方地表1.5倍開挖直徑范圍內隆起。支護壓力上限解分析結果與數值計算結果吻合良好，該研究為盾構隧道施工中支護壓力上限值確定提供了合理理論依據。

淺埋隧道；開挖面；被動失穩；上限分析；支護壓力

隨著城市規模擴大，為了滿足大流量跨區域快速交通要求，隧道成為發展的主流方向，與此同時，城市軌道交通建設也從原來單線隧道逐漸向一次成型的雙線方向發展。目前，上海、南京、杭州、武漢和廣州等地均采用泥水盾構來進行隧道建設。在隧道掘進過程中，常因覆土厚度急劇減小，開挖面先前支護壓力未及時降低，開挖面出現被動失穩并對地表及周邊建筑造成危害。廣東地鐵三號線隧道工程和荷蘭Heinenoord隧道建設過程中均出現了開挖被動失穩事故[1?3]。在淺埋盾構隧道施工過程中，類似風險尤為突出，因此，需要對盾構隧道開挖面被動失穩進行研究以防范類似事故發生。在淺埋盾構隧道被動失穩研究中，主要采用理論分析、數值分析等方法。在理論研究中，LECA等[4]基于上限分析提出了開挖面被動破壞三維機動場；在此基礎上，MOLLON等[5]對機動場進行改進，提出了多椎體被動破壞機動場來近似模擬破壞滑動面；另外，裴紅軍[6]采用極限平衡分析法對三維楔形體模型進行被動失穩分析；陳仁朋等[7?8]對三維楔形體模型進行了改進，推導了開挖面被動失穩支護壓力極限平衡解；HUANG等[9?10]對非均質土體隧道開挖面穩定性進行了二維平面上限分析，為工程實踐提供了重要的理論依據。在理論分析中，被動失穩模式需要預先假設，不能有效充分地擴展真實發展過程，而數值分析方法則可以很好地研究這類問題。VERMEER等[11?12]采用PLAXIS對開挖面失穩形態和開挖面前方土體的應力變化進行了研究，并采用量綱一系數來研究均勻支護壓力。朱偉等[13]用FLAC3D來研究以支護壓力和開挖面中點位移關系為基礎的失穩判據來研究開挖面失穩問題；DIAS等[14]則提出以支護壓力和開挖面中點速度為基礎的開挖面失穩判據研究開挖面失穩；LI等[15]提出不平衡力為基礎的失穩判據來研究泥水盾構開挖面失穩情況，發現主動失穩表現為開挖面整體破壞，被動失穩則是開挖面局部破壞；DIAS等[14]對盾構離心模型試驗進行數值仿真得到與LI等[15]類似的現象。然而，已有數值仿真研究僅發現了開挖面局部被動失穩破壞現象，但對局部被動失穩發展過程和失穩機理探討較少。同時，已有理論研究主要基于開挖面整體被動失穩假設，對分析泥水盾構隧道開挖面支護壓力引起的局部被動破壞具有局限性。本文作者以杭州沿江大道運河隧道工程為背景，采用有限差分法軟件FLAC3D，對泥水盾構隧道掘進面被動失穩進行數值模擬并分析失穩發展過程和失穩模式。在此基礎上，提出泥水盾構掘進面被動失穩二維機動場模型并采用上限分析得到掘進面被動失穩極限支護壓力。

1 工程概況及地質條件

杭州沿江運河隧道是杭州市沿江公路穿越京杭運河的重要節點，位于錢塘江與京杭運河交匯口。運河隧道工程為雙管雙向四車道公路隧道，平行于錢塘江江堤下穿京杭運河，總長1 188 m，盾構段長約551 m。采用2臺泥水盾構自東向西穿越京杭運河。盾構外徑11.65 m，長約11.4 m，刀盤開挖直徑11.68 m，泥水倉泥水重度為11.3 kN/m3。盾構段岸邊地質剖面如圖1所示。隧道穿越場地屬錢塘江流域區，為河口相、淺海相及河流相沉積物。場地淺表層為厚1~5 m的填土，其下為厚度約20 m的粉土和粉砂層，埋深20 m左右以下為粉質黏土，局部夾粉砂，再往下部為含礫粉砂和圓礫層。

盾構在掘進過程中，主要穿越砂質粉土夾黏土土層，上覆土層主要為砂質粉土夾黏土土層、砂質粉土，場地土層物理指標如表1所示。盾構在穿越運河底部時，由于河道水體的作用，需要較大的泥水壓力來維持開挖面穩定。盾構穿越運河后到達隧道接收井處，覆土層厚度由21.3 m迅速減小到5.1 m。在接收井附近區域覆土層很小，同時穿越河底時支護壓力很大，所以，若不及時調整泥水盾構支護壓力，則極易引起開挖面前方土體隆起或者引發土體被動失穩破壞。下面通過數值計算對掘進面被動破壞模式研究并提出理論模型。

單位：m

表1 場地土層分層及其物理力學指標

2 掘進面被動失穩數值分析

2.1 數值模型

在泥水盾構掘進過程中，泥水經盾構上部輸送管道壓入泥水倉，盾構推進力經艙內泥水傳遞到整個掘削面的土體上。當盾構隧道的斷面高度大于中小型直徑盾構的高度時，由泥水容重導致的支護壓力不均勻分布使開挖面上下端的泥水支護壓力之間有很大的差異[1?3]。盾構泥水倉內的不均勻支護壓力如圖2所示。

由于FLAC3D計算中對平衡方程進行動態差分求解，求解過程中由于不生成整體剛度矩陣，有利于大變形問題的求解[16]。應力分量以單元形式存在單元形心處，節點處僅有集中荷載。每次計算后，系統中節點的不平衡力為

圖2 泥水盾構掘進示意圖

(2)

數值模型如圖3所示，模型長為5，寬為3，其中，為盾構直徑。從盾構穿越運河后至接收井附近選取覆土層厚度=0.5，=0.75，=1.00截面進行數值研究。本節采用Mohr?Coulomb本構模型和相關聯流動法則。在數值模擬過程中，在建立地層模型基礎上進行隧道一次性開挖同時對隧道四周施加徑向約束；隨后在開挖面上施加不均勻支護壓力。泥水倉泥水處于流塑狀態，其艙內泥水各向壓力相當，泥水容重引起的不均勻支護壓力的側向壓力梯度為泥水重度，因此，施加在開挖面上不均勻支護壓力和開挖面中心處支護壓力、泥水艙重度的關系為，即開挖面支護壓力可看作由均勻支護壓力疊加上梯度恒為的不均勻支護壓力。VERMEER等[11?12]通過量綱一系數來研究均勻支護壓力，本文也可通過類似量綱一系數來研究梯度不變的非均勻支護壓力。本文也采用最大不平衡力判斷準則研究失穩破壞性狀。因此，在數值計算過程中，通過逐步增大來調節支護壓力(支護壓力梯度保持不變)，為上覆土體重度，同時記錄系統最大不平衡力。

圖3 有限差分網格

2.2 極限狀態分析

選取覆土層最薄處工況/=0.5時為研究對象，系統記錄的最大不平衡力如圖4所示。由圖4可知：當小于3.5時，隨著增大，系統不平衡力隨著計算步增大經歷了迅速增加至峰值然后逐步下降最終趨近于0的過程，不平衡力趨近于0表明系統整體趨于靜止平衡；隨著增大，計算過程中不平衡力峰值逐步增大；當等于3.5時，隨著計算步增加，最大不平衡力從峰值下降但不再趨近于0，表明此時系統局部處于不平衡狀態。綜上分析，認為當=3.5時，開挖面處于被動失穩極限狀態。基于以上分析結果，下面研究開挖面處于被動極限狀態的土體變形規律。

圖4 最大不平衡力監測值

2.3 局部失穩模式及極限支護壓力分析

土體失穩極限狀態速率場如圖5(a)所示。由圖5(a)可以看出：位于開挖面上部土體向前方突出速度顯著，而開挖面下部土體基本還處于靜止狀態。速率場從開挖面上部發展至地表，速率場內靠近開挖面上部局部區域速度較大，速度矢量表明該區域已經貫通形成連續一致的運動體系。此時觀察土體位移場(圖5(b))可以發現：開挖面上部土體向外突出變形明顯，而開挖面下部土體變形微小，開挖面頂部局部土體出現較大變形。結合速率場和位移場云圖可以發現此時支護壓力會引起開挖面發生局部被動失穩而非整體失穩。此處定義局部失穩率對局部失穩程度進行評價(其中，為掘進面局部失穩區域底部至隧道拱頂的距離)。

(a) 速率場；(b) 位移場

：1—2.0; 2—3.0; 3—3.5。

：1—2.0; 2—3.0; 3—3.5。

C/D：1—0.50; 2—0.75; 3—1.00。

數值研究結果表明：在淺埋盾構開挖面在支護壓力增加情況下，開挖面上部分土體經歷彈塑性變形階段直至發生被動失穩，與此同時，開挖面下部分土體則保持穩定。相比整體被動失穩，支護壓力過大更容易引發開挖面局部被動失穩，且覆土厚度越小局部失穩現象越明顯。開挖面失穩比率受到覆土厚度影響較大而土體摩擦角變化則影響較小。基于開挖面局部被動失穩現象，提出開挖面局部被動失穩二維機動場模型并采用上限分析對局部被動失穩進行理論研究。

3 開挖面局部被動失穩上限分析

基于上述數值仿真計算結果提出隧道開挖面局部被動失穩二維機動場模型，如圖9所示。機動場為四邊形，局部破壞高度為，，機動場容許速度為并平行于軸線且與相對滑動面夾角等于土體摩擦角，軸線與水平線夾角為。

圖9 局部被動失穩二維機動場

(3)

機動場耗散功率

(5)

(7)

根據上限定理，在機動容許的塑性變形位移速率場相對應的荷載中，極限荷載最小[17]，即塑性極限狀態下，外力所做功率e等于機動容許位移速率場耗散功率v(e=v)，整理得到盾構隧道開挖面中心處失穩極限支護壓力為

(9)

(11)

4 支護壓力分析

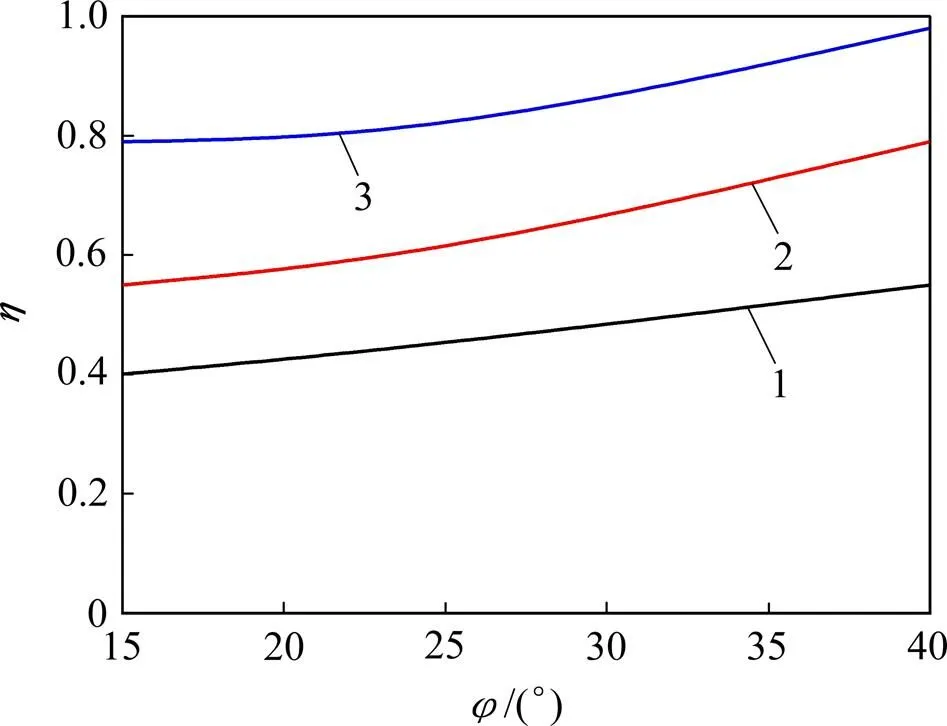
本節主要研究通過局部失穩上限解分析土體摩擦角和開挖面直徑變化對支護壓力的影響，忽略地表荷載作用(0 kPa)。研究發現49°時被動失穩所需支護壓力最小[4]，因此，本文計算中取49°。圖10所示為隨的變化規律。從圖10可以看出：隨著增大，經歷了從逐漸減小至最小值再由最小值逐漸增大的過程。在盾構機支護壓力逐漸增大過程中，首先在支護壓力較小時發生局部失穩破壞，之后隨著支護壓力繼續增大繼而發生整體失穩破壞，因此，選取最小支護壓力為被動失穩極限支護壓力，此時的局部失穩率為被動失穩極限失穩率。由上限分析得出極限失穩隨土體內摩擦角變化規律如圖11所示。由圖11可知：隨著摩擦角逐漸增大，也逐漸增大，但增大幅度較小；然而，從不同覆土厚度來看，其改變較大。另外，從上限分析中得出隧道直徑對沒有影響，這些規律在數值分析過程中也得到了驗證。

圖10 隨變化規律(=24°)

C/D：1—0.50; 2—0.75; 3—1.00。

/：(a) 0.50; (b) 0.75; (c) 1.00

1—本文解；2—數值解；3—解析解[4]；4—解析解[7]。

圖12隨摩擦角變化規律

Fig. 12 Relationship betweenand

5 結論

1) 支護壓力過大會引起盾構局部被動失穩。隨著支護壓力增大，開挖面上部區域內土體經歷了從微小變形直至失穩破壞的過程；與此同時，開挖面下部區域內土體則保持穩定。

2) 覆土層越小，越容易發生局部失穩現象，因此，在淺埋條件下應充分重視局部失穩現象；局部失穩比率主要受覆土厚度的影響，受土體摩擦角的影響較小。

順德逢簡水鄉的商戶幾乎銷售同質的農家菜，如鯪魚肉餅、均安蒸豬、雙皮奶等，存在惡性競爭。由于缺乏相關的餐飲行業規范和認證，僅依靠食品的外觀和宣傳，游客難以判斷食品的質量，只能通過網絡點評或隨大流在最受歡迎的店鋪進行消費，對游客滿意度造成嚴重影響。

3) 提出開挖面局部被動失穩二維機動場，并推導了極限支護壓力上限解。通過對比整體失穩支護壓力解，本文上限解和數值分析更吻合，驗證了該上限解的合理性。

[1] 竺維彬, 鞠世健. 地鐵盾構施工風險源及典型事故的研究[M]. 廣州: 暨南大學出版社, 2009: 10?40. ZHU Weibin, Ju Shijian. Research on the risk sources and typical cases in tunnel construction[M]. Guangzhou: Jinan University Press, 2009: 10?40.

[2] 竺維彬, 鞠世健, 史海鷗. 廣州地鐵三號線盾構隧道工程施工技術研究[M]. 廣州: 暨南大學出版社, 2007: 3?15. ZHU Weibin, JU Shijian, SHI Haiou. Research on the construction technique of 3rd line of Guangzhou shield tunnel[M]. Guangzhou:Jinan University Press, 2007: 3?15.

[3] BEZUIJEN A, BRASSINGA H E. Tunnelling: a decade of progress: Geodelft 1995-2005[M]. Abingdon: Taylor and Francis, 2006: 43?56.

[4] LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material[J]. Géotechnique, 1990, 40(4): 581?606.

[5] MOLLON G, DIAS D, SOUBRA A H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 35(12): 1363?1388.

[6] 裴紅軍. 城市隧道盾構法施工開挖面穩定性研究[D]. 南京: 河海大學地質與巖土工程系, 2005: 3?15. PEI Hongjun. Research for face stability at shield tunneling[D]. Nanjing: Hohai University. Department of Geological and Geotechnical Engineering, 2005: 3?15.

[8] 齊立志. 盾構隧道開挖面被動破壞支護力研究[D]. 杭州: 浙江大學建筑工程學院, 2012: 10?52. QI Lizhi. Study on blow-out face pressure of shield tunnels[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2012: 10?52.

[9] HUANG M, SONG C. Upper-bound stability analysis of a plane strain heading in non-homogeneous clay[J]. Tunnelling and Underground Space Technology, 2013, 38(9): 213?223.

[10] 宋春霞, 黃茂松, 呂璽琳. 非均質地基中平面應變隧道開挖面穩定上限分析[J]. 巖土力學, 2011, 32(9): 2645?2650. SONG Chunxia, HUANG Maosong, Lü Xilin.Upper bound analysis of plane strain tunnel in nonhomogeneous clays[J]. Rock and Soil Mechanics, 2011, 32(9): 2645?2650.

[11] VERMEER P A, RUSE N, MARCHER T. Tunnel heading stability in drained ground[J]. Felsbau, 2002, 20(6): 8?18.

[12] VERMEER P A, VOGLER U. An accuracy condition for consolidation by finite elements[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 1981, 5(1): 1–14.

[13] 朱偉, 秦建設, 盧廷浩. 砂土中盾構開挖面變形與破壞數值模擬研究[J]. 巖土工程學報, 2005, 27(8): 897?902. ZHU Wei, QIN Jianshe, LU Tinghao. Numerical study on face movement and collapse around shield tunnels in sand[J].Chinese Journal of Geotechnical Engineering, 2005, 27(8): 897?902.

[14] DIAS D, JANIN J P, SOUBRA A H, et al. Three-dimensional face stability analysis of circular tunnels by numerical simulations[C]// Proceedings of GeoCongress 2008: Characterization, Monitoring, and Modeling of GeoSystems. Louisiana: ASCE, 2008: 886?893.

[15] LI Y, EMERIAULT F, KASTNER R, et al. Stability analysis of large slurry shield-driven tunnel in soft clay[J]. Tunneling and Underground Space Technology, 2009, 24(4): 472?481.

[16] Itasca Consulting Group Inc. FLAC3D user manual (Version 3.0) [M]. Itasca Ranchettes, USA: Itasca Consulting Group Inc., 2003: 315?324.

[17] 龔曉南. 土塑性力學[M]. 杭州: 浙江大學出版社, 1997: 201?310. GONG Xiaonan. The soil plasticity[M]. Hangzhou: Zhejiang University Press, 1997: 201?310.

(編輯 楊幼平)

Blow-out failure analysis of tunnel face in shallow slurry shield tunneling

LI Fengtao1, 2, TANG Xiaowu1, LIU Wei1, 3, ZHAO Yu4, TANG Qiang3

(1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;2. China Railway Design Corporation, Tianjin 300143, China;3. School of Urban Rail Transportation, Soochow University, Suzhou 215131, China;4. Institute of Disaster Prevention Engineering, Zhejiang University, Hangzhou 310058, China)

Based on Hangzhou canal tunnel project, the explicit differential code FLAC3Dwas applied to investigate the blow-out failure of tunnel face. The case of Hangzhou canal tunnel was investigated, an agreement between the upper bound solution and numerical solution was discovered. The results show that partial failure existing on the up part of face is found instead of integrate failure. The ratio of failure height to tunnel diameter is majorly affected by the cover depth, but little influenced by frictional angles of soils. Furthermore, on the ground surface, the soil upheaving starts where is above the tunnel face. The ratio of upheaving length to the tunnel diameter is 1.5. This study improves the evaluation of the upper limit support pressure for the blow-out failure and the relevant theoretical foundation is cemented.

shallow tunnel; working face; blow-out failure; upper bound analysis; support pressure

10.11817/j.issn.1672-7207.2017.07.018

TU45

A

1672?7207(2017)07?1809?08

2016?08?13；

2016?10?19

國家自然科學基金青年科學基金資助項目(51508503)；國家自然科學基金重點資助項目(51338009)；華東勘測設計研究院科技項目(KY2013-02-30) (Project(51508503) supported by the National Science Foundation for Young Scientists of China; Project(51338009) supported by the National Natural Science Foundation of China; Project(KY2013-02-30) supported by the Research Plan of Huadong Engineering Corporation)

唐曉武，教授，從事環境土工與地下工程研究；E-mail: tangxiaowu@zju.edu.cn