極限風況下不同基礎形式的風電機組塔架荷載估計

文|許楠

極限風況下不同基礎形式的風電機組塔架荷載估計

文|許楠

目前，從陸上風電機組到海上風電機組，隨著離岸距離和水深的增加，基礎形式分為陸上的固定式，近海的底部固定式和浮體式。以往研究大都只針對某一種基礎結構形式來研究塔架的荷載。研究表明，不同的基礎形式會產生不同的塔架荷載，對于浮體式風電機組，數值模擬是常用的荷載評估方法，鑒于固定基礎模型不適用于計算浮體式風電機組的塔架荷載，因此有必要構建一種通用的荷載計算模型，從而可以運用解析公式來估計極限風況下的塔架荷載。本文提出了SR （Sway-Rocking） 模型作為任意基礎形式的風電機組通用的荷載計算模型。SR模型可將復雜的浮體式風力發電機組的錨固體系簡化為一個橫向的彈簧及阻尼器和一個轉動的彈簧及阻尼器，兩個彈簧的剛度和兩個阻尼器的阻尼可以通過FEM （Finite Element Model） 分析來獲取。通過改變彈簧剛度和阻尼器阻尼可以模擬不同的基礎形式風電機組的塔架荷載，從而可以利用等效靜力荷載方法和模態分析來推導極限風況下塔架荷載的理論計算公式。對于每一種基礎形式，理論公式均已由動力響應分析驗證。

風電機組、基礎與錨固體系

本文研究風荷載的模型選取半潛式浮體作為基礎，錨固體系分別采用張力腿和懸鏈線體系，浮體之上安裝NREL 5MW型號風電機組。浮體的詳細參數參見表1：張力腿錨固體系，考慮到盡量消減浮體的縱搖效應，3條張力索分別連接浮體的3個角柱，參照圖1（a）；懸鏈線錨固體系由3條400m跨度的錨鏈共同連接在中心柱的底端，相鄰錨鏈水平投影的夾角為120°，其中一條沿入射波的方向伸展，參照圖1（b）；風電機組的詳細參數參見表2。本文采用FEM計算程序來驗證塔架荷載的解析公式，程序可以考慮風電機組、浮體及錨固體系之間的耦合特性。

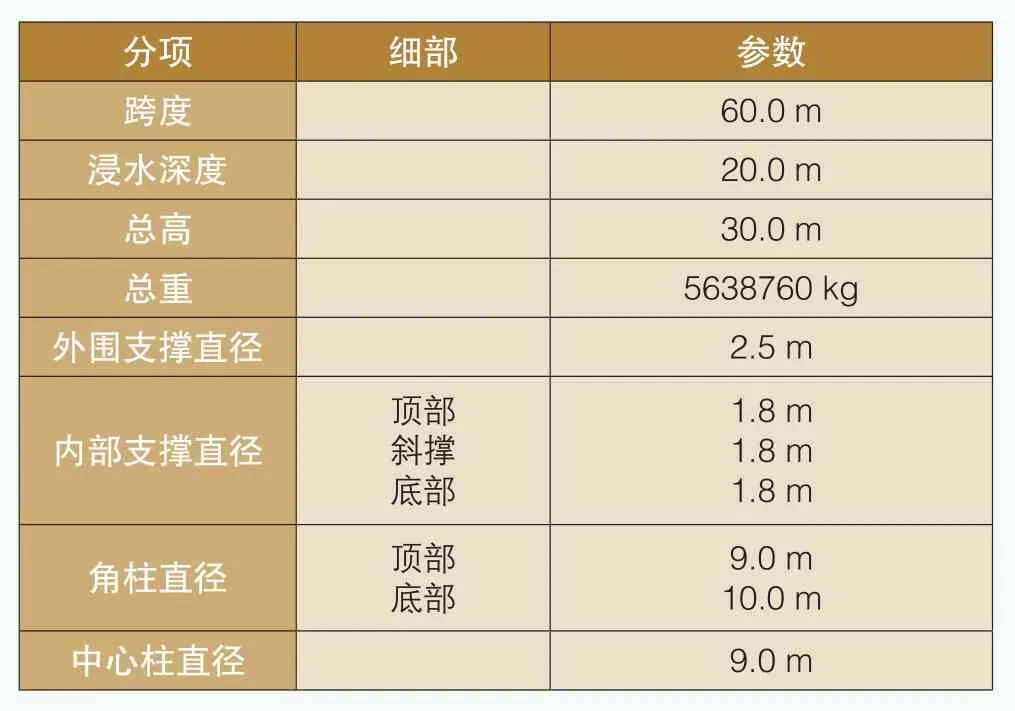
表1 半潛式浮體的參數

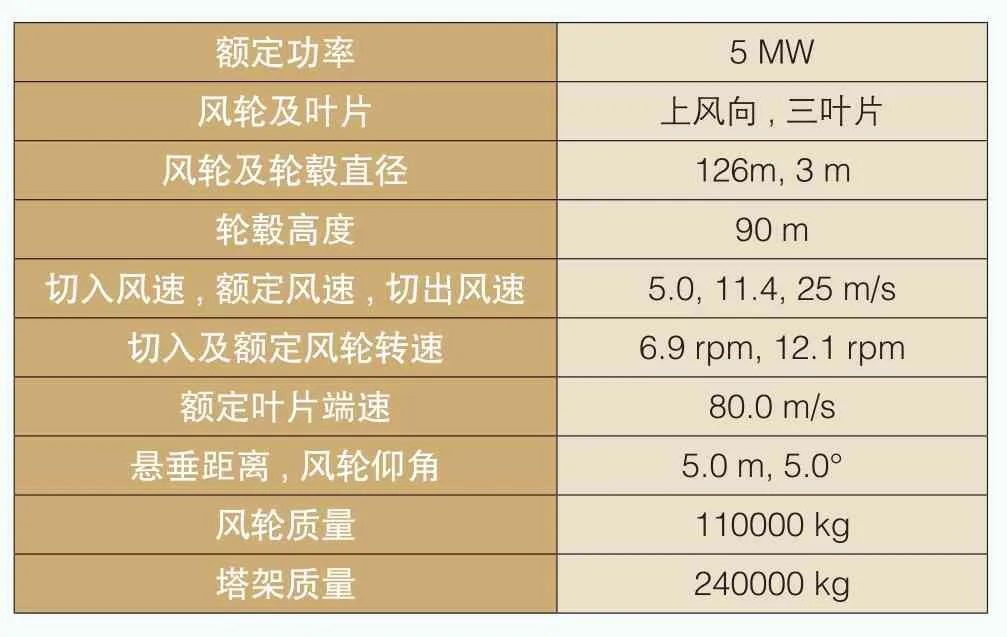
表2 NREL 5MW風電機組的參數

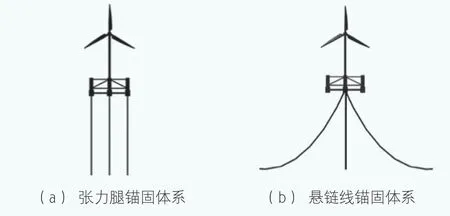
圖1 本文研究的錨固體系

SR（Sway-Rocking）模型

縱移和縱搖是浮體6個自由度運動（如圖2）中最為顯著的兩個，其他方向的運動可以忽略。因此，本研究借鑒地震工程中常用的SR模型（如圖3）作為等效計算模型模擬浮體運動對塔架荷載的影響。SR模型可將復雜的錨固體系簡化為兩個方向的彈簧和阻尼器：縱移用一個橫向的彈簧和阻尼器模擬，縱搖用一個轉動的彈簧和阻尼器模擬。與地震工程不同的是等效剛度kS， kR和阻尼cS， cR需通過FEM分析來獲取。

采用完整的浮體風電機組體系模型，將上部結構（風電機組和浮體）視為剛體，橫向頻率ωS和轉動頻率ωR可以通過FEM數值模擬體系的自由振動獲得。因此，兩個彈簧的剛度可按下式計算：

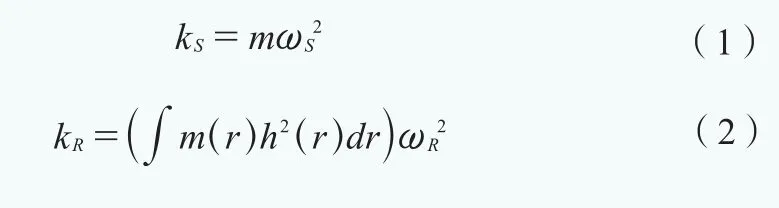
式中，m是風電機組和浮體的總質量， m(r)是r位置處的單位長度質量，h(r)是距離塔架底部的高度。 由于浮體被看作是塔架底部的集中質量，不考慮其尺寸的影響，因此公式（2）中僅在風電機組部分做積分。另外，兩個阻尼器的阻尼也可以由FEM數值模擬進行估計。將上部結構的多自由度體系簡化為等效單自由度模型，同時考慮了橫向和轉動運動，通常被稱作壓縮SR模型（圖4）。單自由度體系的質量，剛度，阻尼比分別為me，ke，ce。

由于第一階振動模態對風電機組塔架的風荷載貢獻最為顯著，而高階頻率在風荷載譜中所占的能量非常小，所以本研究忽略高階模態的影響，只考慮第一階模態。圖4的壓縮SR模型的第一階固有周期T1可以由固定基礎模型的第一階固有周期Tf，橫向固有周期TS和轉動固有周期TR計算，如公式（3）所示。

要計算壓縮SR模型的阻尼比，需考慮一個循環振動周期T1內的應變能E和吸收的能量ΔE，則第一階模態的阻尼比ξ1推導如下：

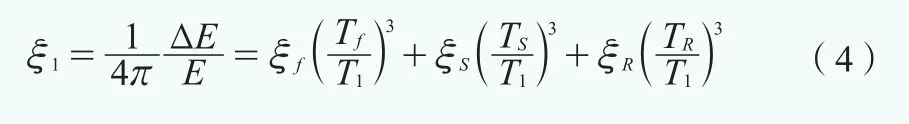
式中，ξf是固定基礎模型的第一階阻尼比，ξs是橫向阻尼比，ξR是轉動阻尼比。計算SR模型的第一階固有周期T1和阻尼比ξ1的必要參數見表3。

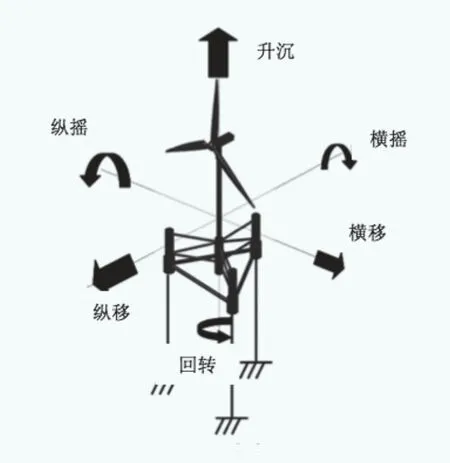
圖2 浮體式風電機組體系的運動

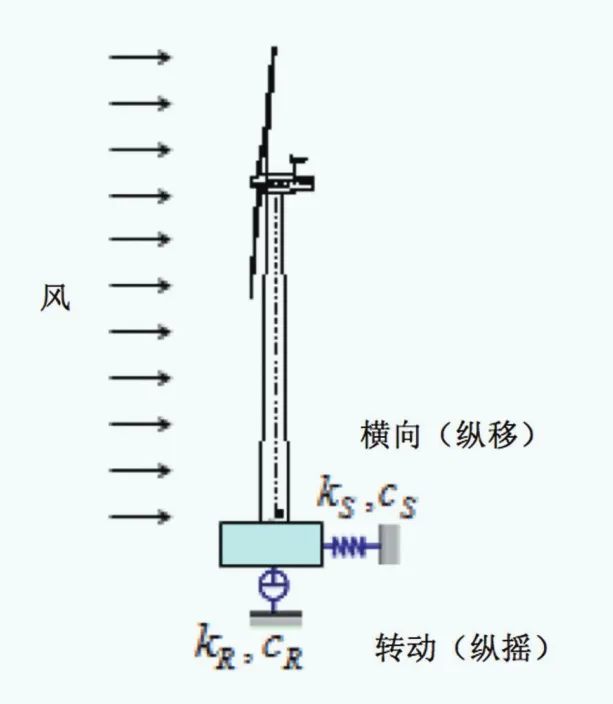
圖3 Sway-Rocking 模型

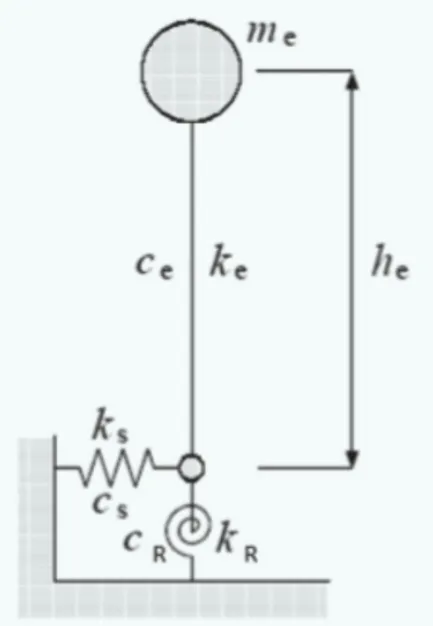
圖4 壓縮SR模型

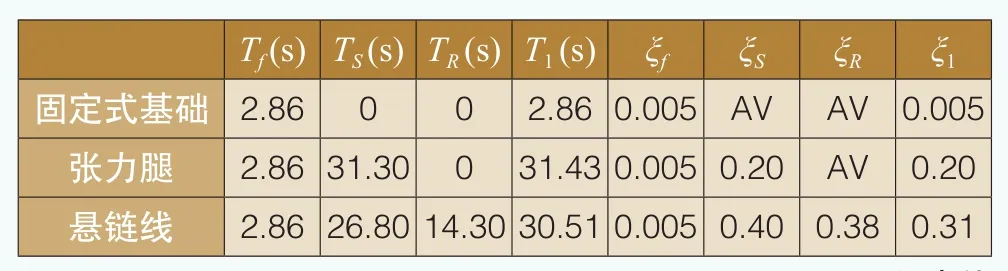
表3 周期和阻尼比

風荷載估計

與固定式基礎的風電機組一樣，作用在塔架上的最大風荷載依然可采用等效靜風荷載公式計算，其中平均風荷載的計算也與固定式基礎無差異。由于平均風荷載依賴于風本身，所以在相同風況下，不同基礎形式的塔架平均風荷載是相同的。標準差也同樣包含了背景部分σB和共振部分σR：

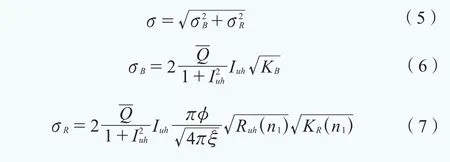
式中，Iuh為輪轂高度處的湍流強度，Q為平均風荷載，φ為振型修正系數，Ruh（n1）為標準化的功率譜密度，KB和 KR（n1）分別為背景和共振分量的尺寸折減系數，n1為塔架的第一階固有頻率，ξ為阻尼比。KB可按下式計算：

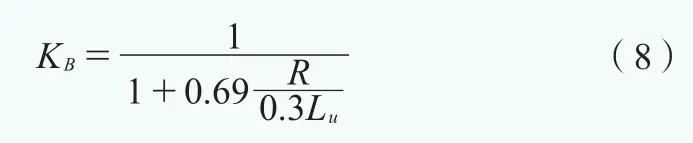
式中R為風輪半徑，Lu為湍流積分尺度。因此，與平均風荷載一樣，不同基礎形式的背景標準差是相同的，因為它只依賴于風本身和風電機組尺寸。但是共振分量是?，Ruh（n1），KR（n1）和ξ的函數，因此除了風本身它還和結構自身的振動特性有關，所以會隨著基礎形式而發生變化。振型修正系數?與振型和模態質量有關，從圖5可以看出 ，固定基礎模型的振型修正系數比SR模型的稍低，但并不顯著。

標準化的風速譜Ruh（n1）和共振分量的尺寸折減系數KR（n1）以及阻尼比ξ表示如下：

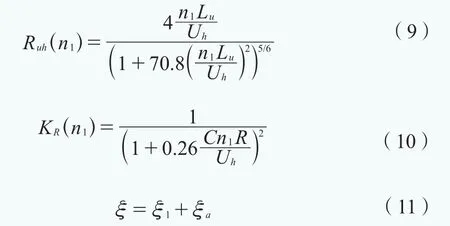
式中Uh為輪轂高度處的平均風速，C為無量綱的衰減因子，ξ1為系統的阻尼比，ξa為氣動阻尼比。

圖6和圖7給出了標準化風速譜Ruh（n1）和共振分量的尺寸折減系數KR（n1）隨第一階固有頻率的變化。從圖中可以看出，由于固定基礎模型的固有頻率值比SR模型高，所以其Ruh（n1）和KR（n1）的值要比SR模型低很多。因此，對于浮體式風電機組如采用固定基礎模型，會低估其共振標準差。

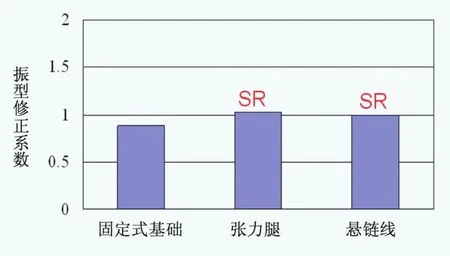
圖5 振型修正系數φ的比較

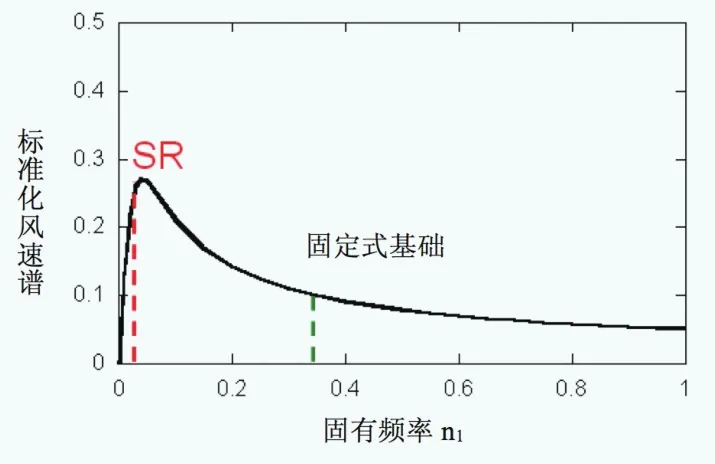
圖6 標準化風速譜的比較

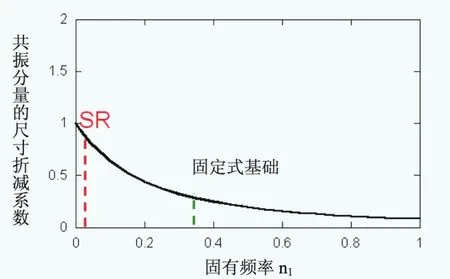
圖7 共振分量的尺寸折減系數的比較

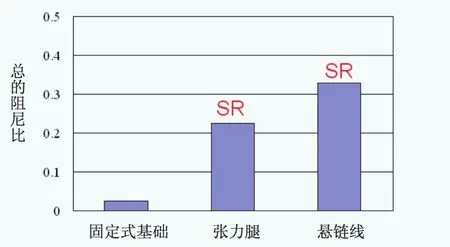
圖8 總的阻尼比ξ的比較

由于不同基礎形式的風電機組的氣動阻尼比是相當的，這樣差異較大的系統阻尼比會導致不同基礎形式的總的阻尼比的差異較大。從圖中可以看出，固定基礎模型的總阻尼比要比SR模型的低很多，這就造成了采用固定基礎模型會高估浮體式風電機組的共振標準差。

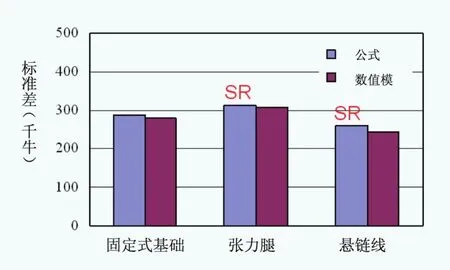
圖9 標準差的比較

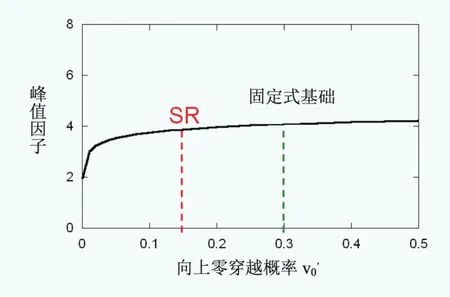
圖10 峰值因子的比較

以上分析可以看出，第一階固有頻率和系統阻尼比是估計塔架荷載的兩大控制因素，而固定基礎模型在這兩個因素上與SR模型有著較大差異，所以固定基礎模型不能用來計算浮體式風電機組體系的風荷載。如圖9所示，對于不同的基礎形式，利用SR模型提出的計算公式都可以給出與數值模擬接近的結果。另外，懸鏈線體系風電機組的標準差比張力腿體系的低，也是由于其較大的阻尼比引起的（圖8）。

塔架荷載的非高斯峰值因子是向上零穿越概率以及偏度的函數。對于不同的基礎形式，偏度無較大差異，而且由于海上的低湍流度，偏度值很低；向上零穿越概率受第一階固有頻率影響較大，所以固定基礎模型和SR模型的向上零穿越概率差異較大。圖10給出了峰值因子隨向上零穿越概率的變化，可以看出峰值因子隨向上零穿越概率變化不大。因此，兩種模型有著接近的峰值因子。

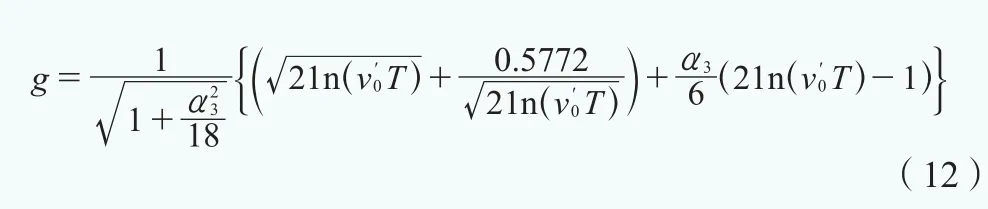
結論

本文提出了SR模型作為任意基礎形式的風電機組的通用荷載計算模型。SR模型可以考慮浮體運動對塔架荷載的影響，通過改變彈簧剛度和阻尼器阻尼可以模擬不同的基礎形式的塔架荷載，從而利用等效靜力荷載方法和模態分析推導了極限風況下塔架上的風荷載的理論計算公式。本文比較了固定式基礎和浮體式基礎（張力腿和懸鏈線）的風電機組塔架上的風荷載。由理論公式可以看出，對于不同的基礎形式平均風荷載和標準差的背景分量是相同的，這是因為它們是由風本身決定的；但是標準差的共振分量是不同的，因為它還依賴于結構自身的振動特性。研究發現，第一階固有頻率和系統阻尼比是估計塔架荷載的兩大控制因素，而固定基礎模型在這兩個因素上與SR模型有著較大差異，所以傳統的固定基礎模型只能用于陸上風電機組，而SR模型適用于任意基礎形式的風電機組。本研究還發現非高斯峰值因子對基礎類型不敏感。

（作者單位：中國廣核新能源控股有限公司）