電液位置伺服系統的頻域設限加權切換控制

陳 剛 曹 賽 王益群 趙團民

1.燕山大學國家冷軋板帶裝備及工藝工程技術研究中心,秦皇島,0660042.燕山大學機械工程學院,秦皇島,0660043.中國重型機械研究院股份公司板帶軋制裝備研究所,西安,710032

電液位置伺服系統的頻域設限加權切換控制

陳 剛1, 2曹 賽2王益群1, 2趙團民3

1.燕山大學國家冷軋板帶裝備及工藝工程技術研究中心,秦皇島,0660042.燕山大學機械工程學院,秦皇島,0660043.中國重型機械研究院股份公司板帶軋制裝備研究所,西安,710032

分析電液位置伺服系統二階狀態反饋(DOSF)控制系統存在靜差的機理，設計三階無靜差狀態反饋(TOSF)控制器。為克服TOSF控制系統階次高的缺陷，以切換頻域設限加權算法實現TOSF-DOSF雙控制器切換控制，切換頻域設限減小了控制作用量對加權系數變化的靈敏度。仿真結果表明：電液位置伺服DOSF控制系統靜差與負載彈性剛度正相關，TOSF控制系統能消除系統靜差且符合動態性能設定。測試實驗結果表明：TOSF-DOSF雙控制器頻域設限加權切換控制使系統具有良好的動靜態性能，與閾值切換相比，具有較小的切換沖擊。

電液位置伺服; 狀態反饋; 靜差; 切換頻域設限

0 引言

參數非線性、不確定性和時變性等因素導致電液伺服系統存在模型誤差，該誤差限制了狀態反饋控制系統動態性能的提高[1]。反饋線性化能消除系統中具有的非本質非線性，對于本質非線性，局部線性化處理適用的工作范圍不大[2-3]。參數自適應辨識雖可提高模型精度，但會導致系統階次升高，可靠性降低[4-6]。模糊控制通過模糊規則能對智能經驗加以利用，適用于低精度模型的控制[7]，神經網絡控制通過訓練機制提高模型精度從而優化控制性能[8]，但因智能控制器結構復雜，所以其參數的整定難度大。滑模變結構控制和H∞控制可降低模型誤差對狀態反饋控制性能的影響[9-12]，但控制性能指標選取較保守。

本文將設計的無靜差三階狀態反饋(three-order state feedback,TOSF)控制器與傳統二階狀態反饋(double-order state feedback,DOSF)控制器相結合，實現對控制器切換控制。而切換過程的平滑性直接影響控制性能的優劣，目前較為有效的方法是使切換過程在模糊化了的邊界中進行，減弱抖動，使切換過程平滑(但僅延長切換時間而并未減小切換總量[13-14])，因此，筆者設計頻域設限加權切換算法減小控制作用量對切換過程的靈敏度，以達到進一步減小切換沖擊的目的[15]。

1 數學建模

圖1為電液位置伺服系統示意圖，其油缸力平衡方程、流量連續性方程、伺服閥線性化流量方程和閥芯位移方程如下：

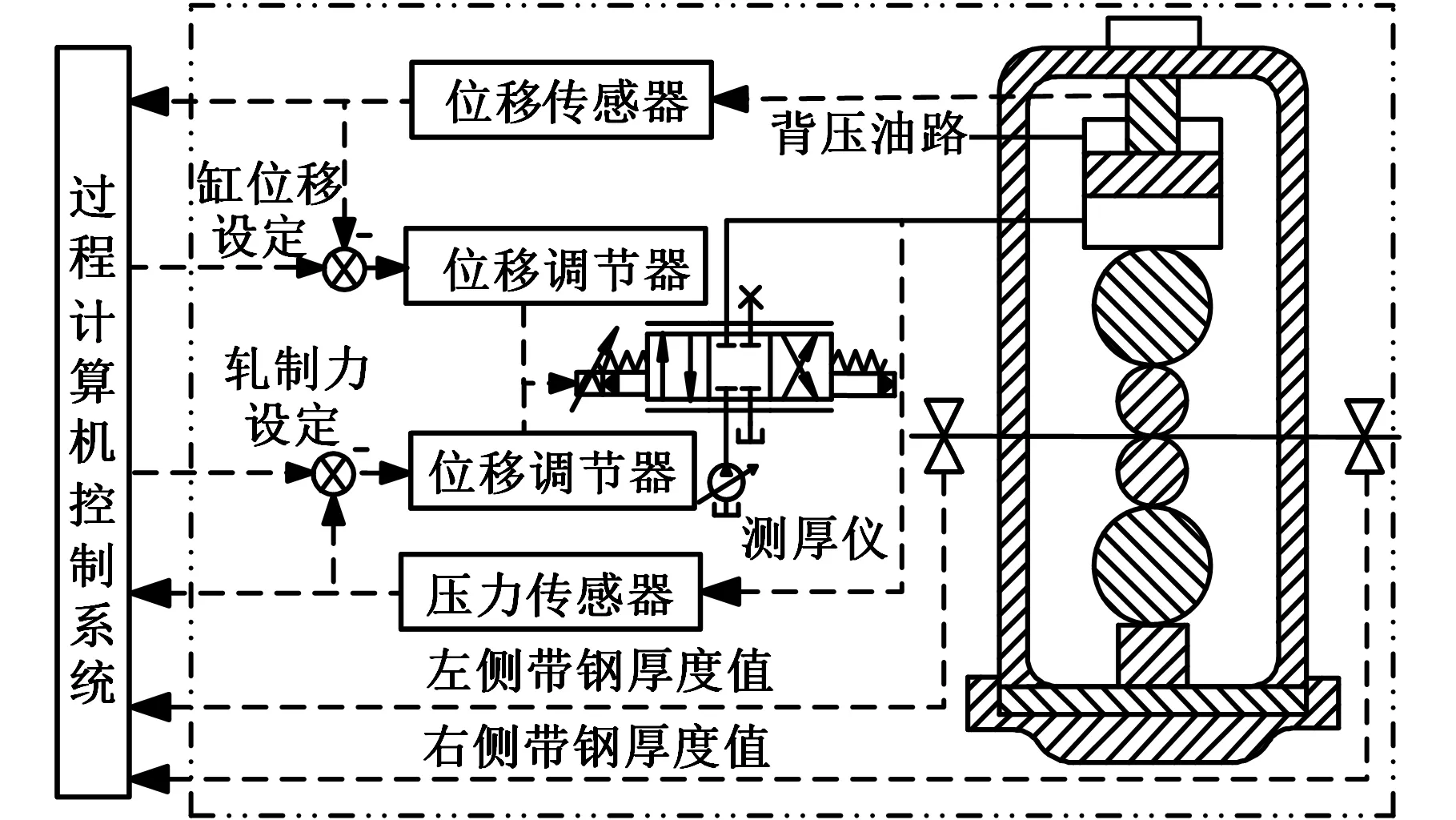
圖1 電液位置伺服系統示意圖Fig.1 Electro-hydraulic position servo system schematic diagram

(1)

(2)

qVL(t)=Kqxv(t)-KcpL(t)

(3)

(4)

式中，pL(t)為油缸負載壓力；Ap為油缸活塞工作面積；mt為活塞和負載運動部件總質量；xp(t)為油缸活塞位移，對應于軋機輥縫；Bp為活塞及負載黏性阻尼系數；K為負載彈性剛度；FL(t)為外負載力；qVL(t)為負載流量；Ctp為油缸總泄漏系數；Vt為缸油液體積變化量；βe為油液體積彈性模量;Kq為伺服閥流量增益；xv(t)為伺服閥閥芯位移；Kc為伺服閥流量壓力增益;u(t)為指令信號；Ka為伺服放大器增益；Kv為伺服閥閥芯運動增益；Tsv為伺服閥慣性時間常數。

狀態向量x(t)=(x1(t),x2(t))T,選取x1(t)=qVL(t)、x2(t)=xp(t)，輸出為y(t)=xp(t)。基于以下假設建立狀態空間模型：①忽略Bp的影響；②控制系統開環頻率特性的剪切頻率遠小于油缸無阻尼自然振蕩角頻率。聯立式(1)～式(4)得系統狀態空間表達式為

(5)

式中，A、B、C分別為系統矩陣、控制矩陣和輸出矩陣。

由式(5)可見，系統被表示為一個二階的狀態反饋系統(DOSF系統)，其狀態反饋表達式為

u(t)=lr(t)-Hx(t)

(6)

式中，H為狀態反饋增益向量，H=(h1，h2)；l為參考信號增益；r(t)為給定信號。

2 電液位置伺服DOSF控制靜差分析

聯立式(5)、式(6)得電液位置伺服DOSF控制系統的狀態空間表達式和閉環傳遞函數如下：

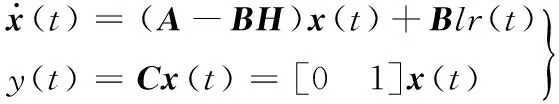
(7)

Gb(s)=C(sI-A+BH)-1Bl

(8)

式中，s為拉普拉斯算子；I為單位陣；Gb(s)為DOSF系統閉環傳遞函數。

結合式(5)，可將式(8)轉化為

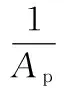
(9)

(10)

取

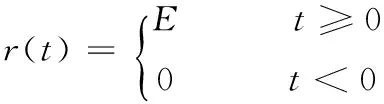
其中，E為階躍幅值，取非零實數。

靜差

(11)

將式(10)代入式(11)得

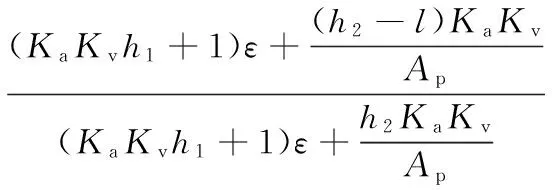
(12)

DOSF控制系統取l=h2，有

ess=

(13)

結論1 對由受控系統式(5)和狀態反饋式(6)構成的系統，若令參考信號增益l=h2，則當且僅當ε=0時，系統無靜差。

結論1表明，電液位置伺服DOSF控制系統存在靜差是由于ε非零。結合式(10)，即負載彈性剛度K和伺服閥壓力流量系數Kc及油缸總泄漏系數Ctp非零。式(10)、式(13)表明，對于電液位置伺服DOSF控制系統，靜差與負載彈性剛度K正相關。

3 電液位置伺服TOSF控制系統設計

采用動態反饋算法設計三階無靜差控制器。給定r(t)參考模型為

(14)

式中，xr(t)為系統狀態；Ar、Cr分別為系統矩陣和輸出矩陣。

令φ(s)=sm+αm-1sm-1+…+α1s+α0為Ar最小多項式位于s右半閉平面的根因式，t→∞時r(t)不趨于零部分的模型為

(15)

式中，xc(t)為狀態向量；yc(t)為輸出。

定理1[16]SISO受控系統(式(6))可按式(17)～式(20)實現無靜差控制的充分必要條件為：對φ(s)=0的根si(i=1,2,…,m)來說，

(16)

成立。其中，n為方陣A的階數。

若給定r(t)為階躍信號，則φ(s)=s，t→∞時，r(t)不趨于零部分的模型為

(17)

φ(s)=0的根滿足式(16)，據定理1，系統無靜差。

結合參考模型，將原系統轉化為三階狀態反饋控制系統(TOSF控制系統)，其狀態方程、輸出方程和狀態反饋為

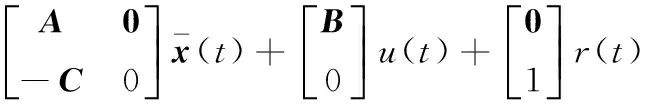
(18)

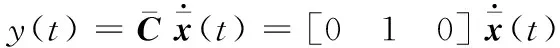
(19)

(20)

將式(20)代入式(18)得狀態反饋后系統矩陣如下：

(21)

狀態反饋期望特征多項式為

(22)

式中，psi(i=1,2,3)為狀態反饋期望極點。

(23)

4 頻域設限加權切換

為克服TOSF控制系統階次高的缺陷，以切換頻域設限加權算法實現TOSF-DOSF雙控制器切換控制。

定義1υ(t)=(υ1(t),υ2(t))為時域函數υ1(t)和υ2(t)構成的向量，t0時刻切換運算為

(24)

(25)

式中，g1(t-t0)、g2(t-t0)分別為υ1(t)、υ2(t)的傅里葉變換時的窗函數；R為實數域；ω為角頻率。

稱式(25)為τ(t0)υ(t)的切換沖擊范數，用來表征最大切換沖擊強度。

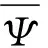
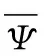
(26)

式(26)的充分條件為

(27)

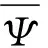
GΨ(s)=GΨN(s)GΨD(s)-1

(28)

(29)

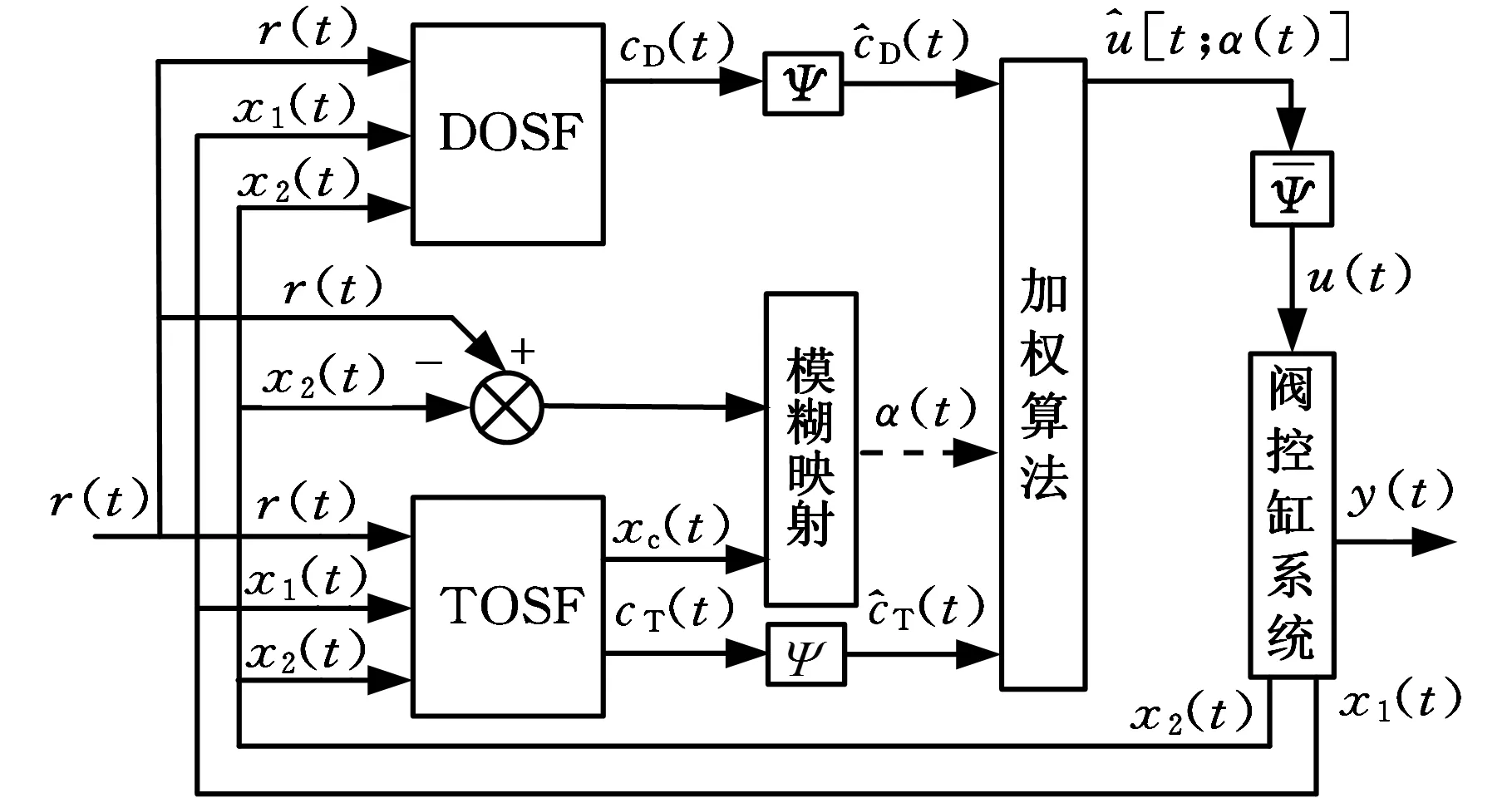
圖2 TOSF-DOSF頻域設限加權切換控制Fig.2 TOSF-DOSF finite frequency domain weighted switching control

模糊映射為

α(t)=Fuzzy(xc(t),r(t)-x2(t))

(30)

加權算法為

(31)

有

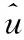
(32)

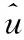
(33)

式中，Δα(t)為α(t)的增量。

構造向量

結合式(32)、式(33)有

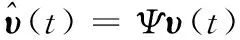
(34)

由式(34)，具有切換頻域設限的切換范數可轉化為

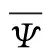
(35)

無切換頻域設限的切換范數為‖τ(t)υ(t)‖，結合式(26)可知，切換頻域設限可減小切換范數對加權系數α(t)變化的靈敏度。

加權系數α(t)通過模糊推理獲得。設xc(t)、r(t)-x2(t)、α(t)對應的語言變量分別為X1、X2和U。X1、X2的論域歸一化為[-1,1]，語言值為{N(負)、Z(零)、P(正)}。U的論域歸一化為 [0,1]，語言值為{Z(零)、PS(正小)、PM(正中)、PB(正大)}，見表1。隸屬度函數采用三角形函數，基于表1模糊規則采用T-S算法進行推理，以重心法對模糊推理輸出解模糊化處理，得模糊映射見圖3。

表1 加權系數模糊規則

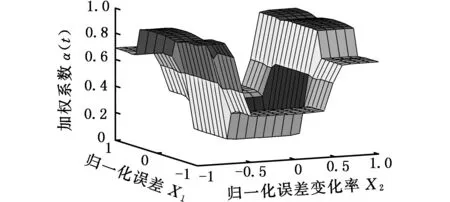
圖3 模糊映射Fig.3 Fuzzy mapping

5 仿真

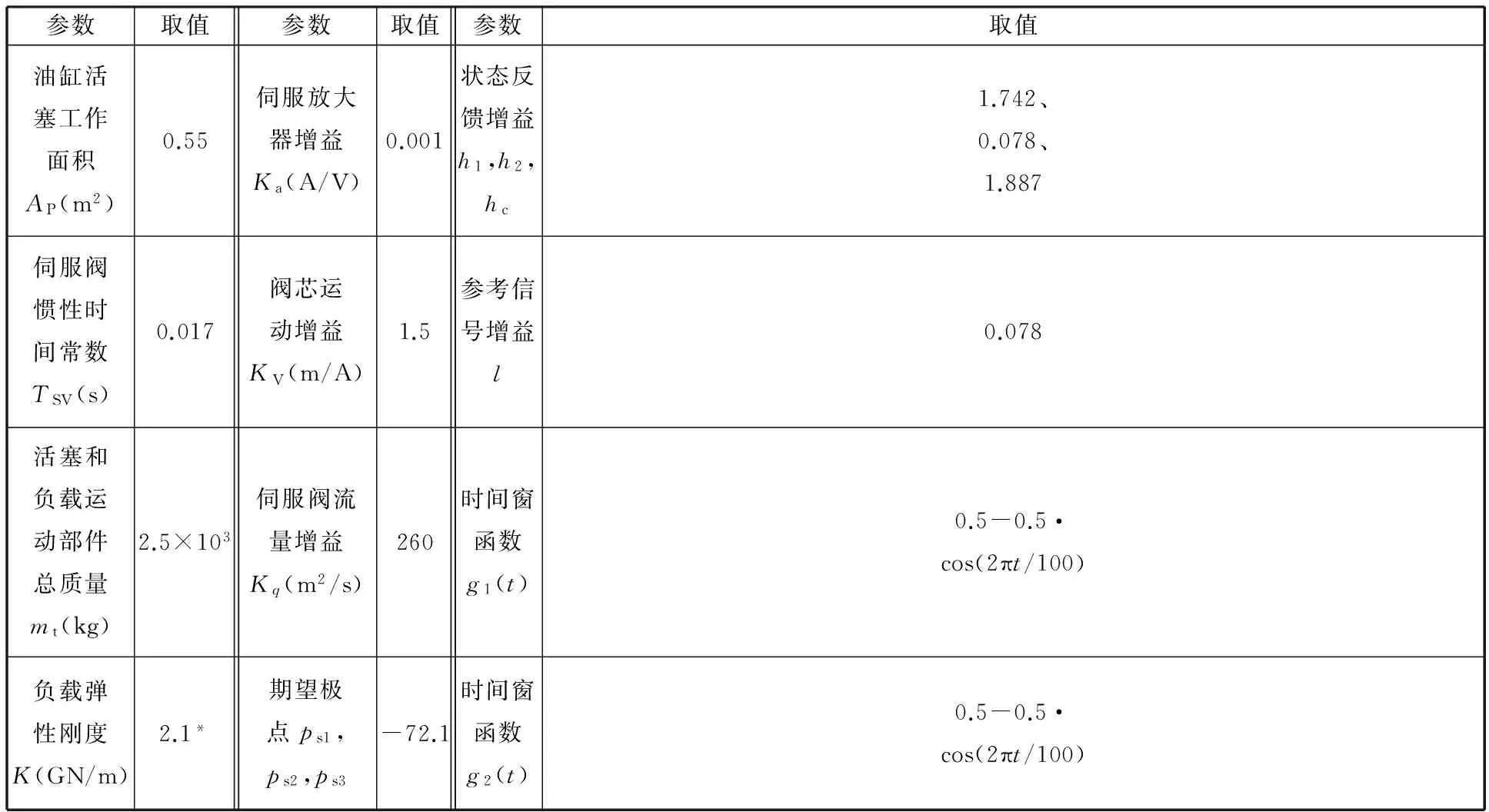
表2 系統主要參數值

注：*僅針對圖4仿真曲線。

表3 負載彈性剛度對DOSF系統靜差的影響

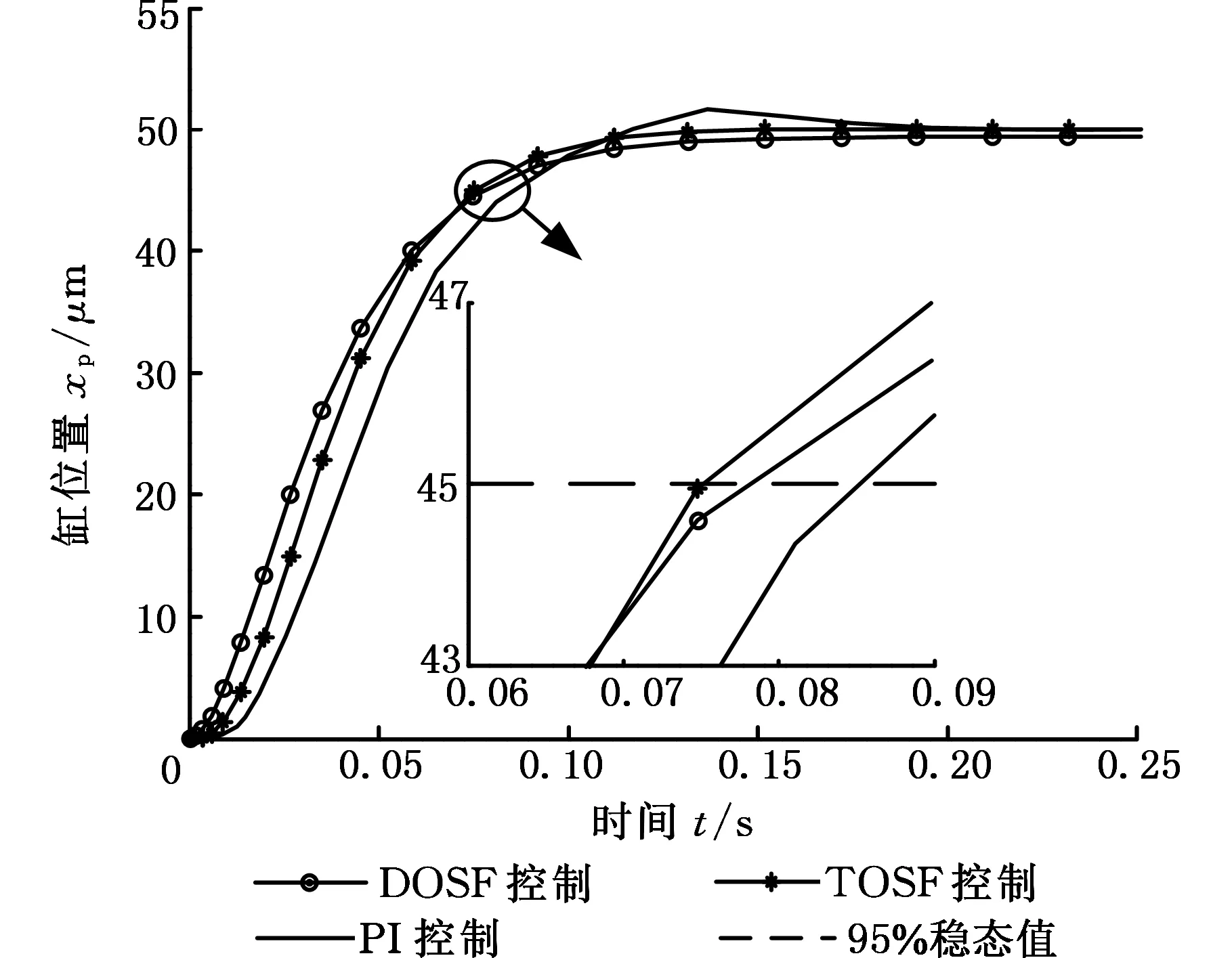
圖4 TOSF控制、DOSF控制與PI控制的性能對比仿真曲線Fig.4 The performance-contrast simulation curve among TOSF, DOSF and PI

6 實驗

在圖5所示某冷連軋機組上進行電液伺服位置系統的狀態反饋控制性能測試實驗，閥流量狀態的獲取通過降維觀測器實現。根據式(27)，選取切換頻域設限算子如下:

GΨN(s)=0.2s2+s

(36)

GΨD(s)=0.01s2+0.2s+1

(37)

(38)

(39)

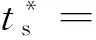
(a)軋機機架

(b)主操作臺 (c)測試系統 圖5 進行測試實驗的某冷連軋機組Fig.5 The cold rolling machine on experimental tests

(a)DOSF控制(采樣周期15.63 ms)

(b)TOSF-DOSF雙控制器頻域設限切換控制(采樣周期15.63 ms)圖6 控制性能對比實驗曲線Fig.6 The control performance contrast experiment curves

7 結論

(1)電液位置伺服DOSF控制系統存在靜差是由于負載彈性剛度K、伺服閥的壓力流量增益Kc和油缸的總泄漏系數Ctp非零。靜差與負載彈性剛度K正相關。

(2)電液位置伺服TOSF控制系統能同時實現無靜差和動態性能設定，具有良好的動靜態綜合性能指標。

(3)TOSF-DOSF雙控制器切換控制系統克服了TOSF控制系統階次高的缺陷；頻域設限加權切換較閾值切換可減小TOSF與DOSF控制器間的切換沖擊。

(a)閾值切換系統的控制量

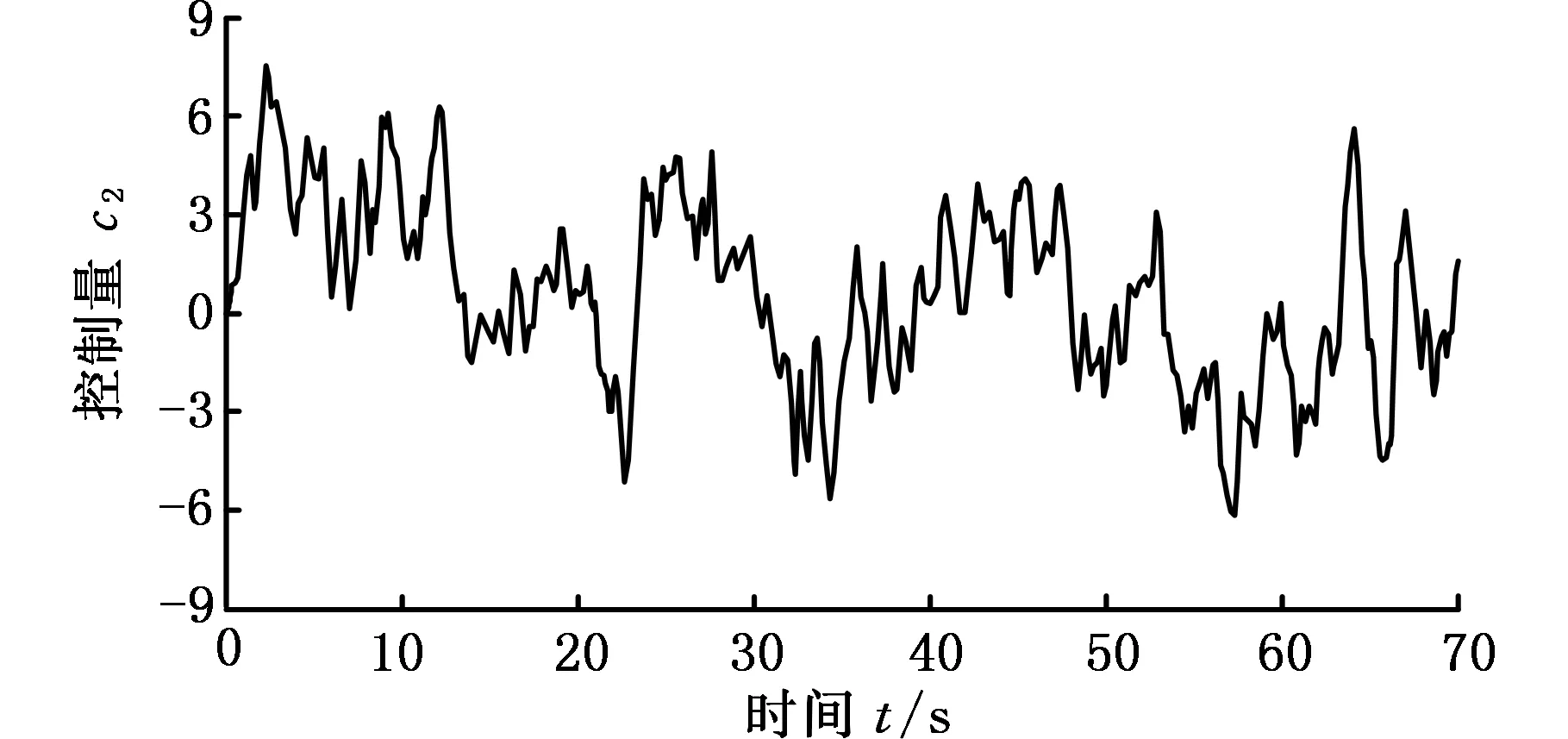
(b)頻域設限切換系統的控制量

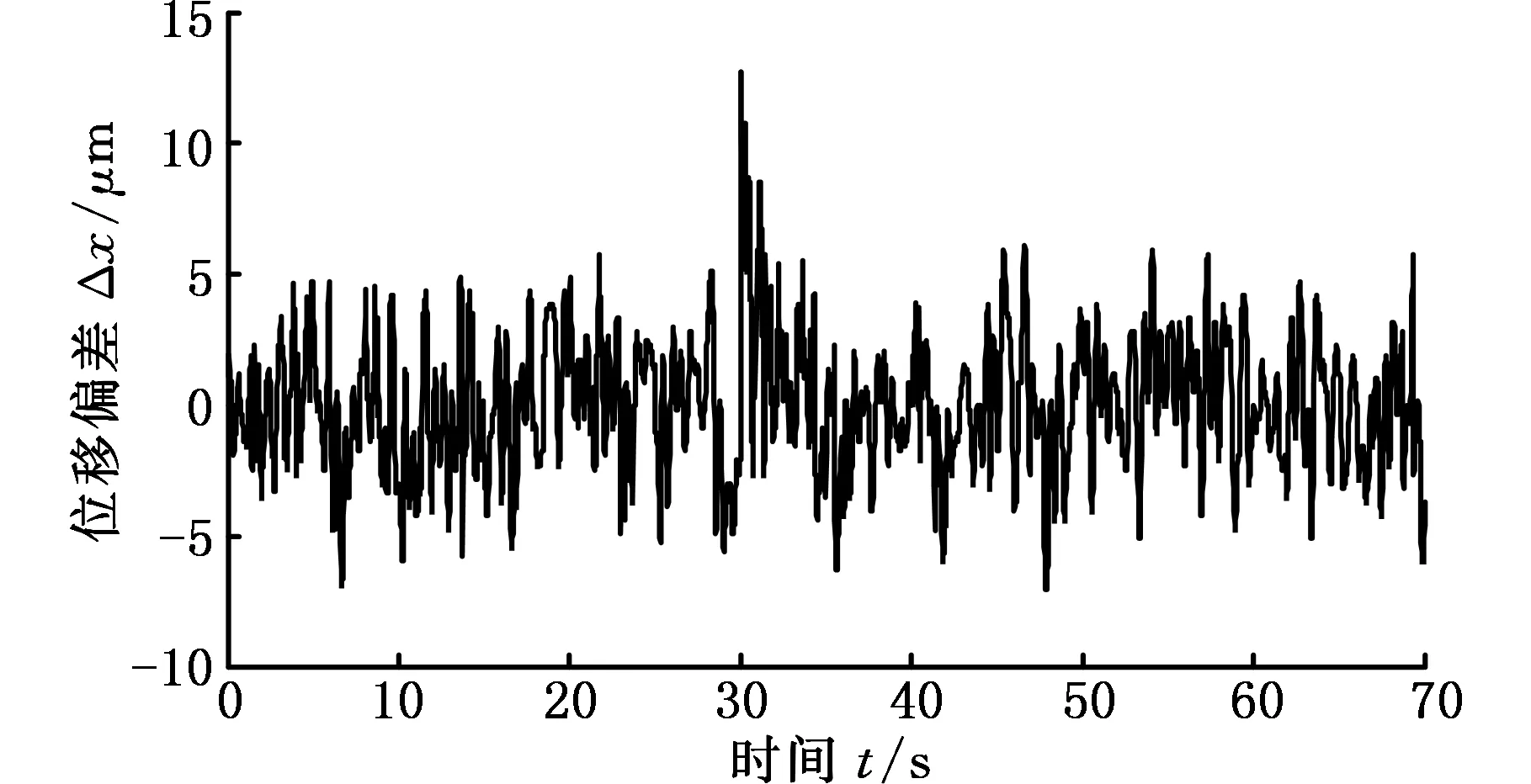
(c)閾值切換系統的位移偏差

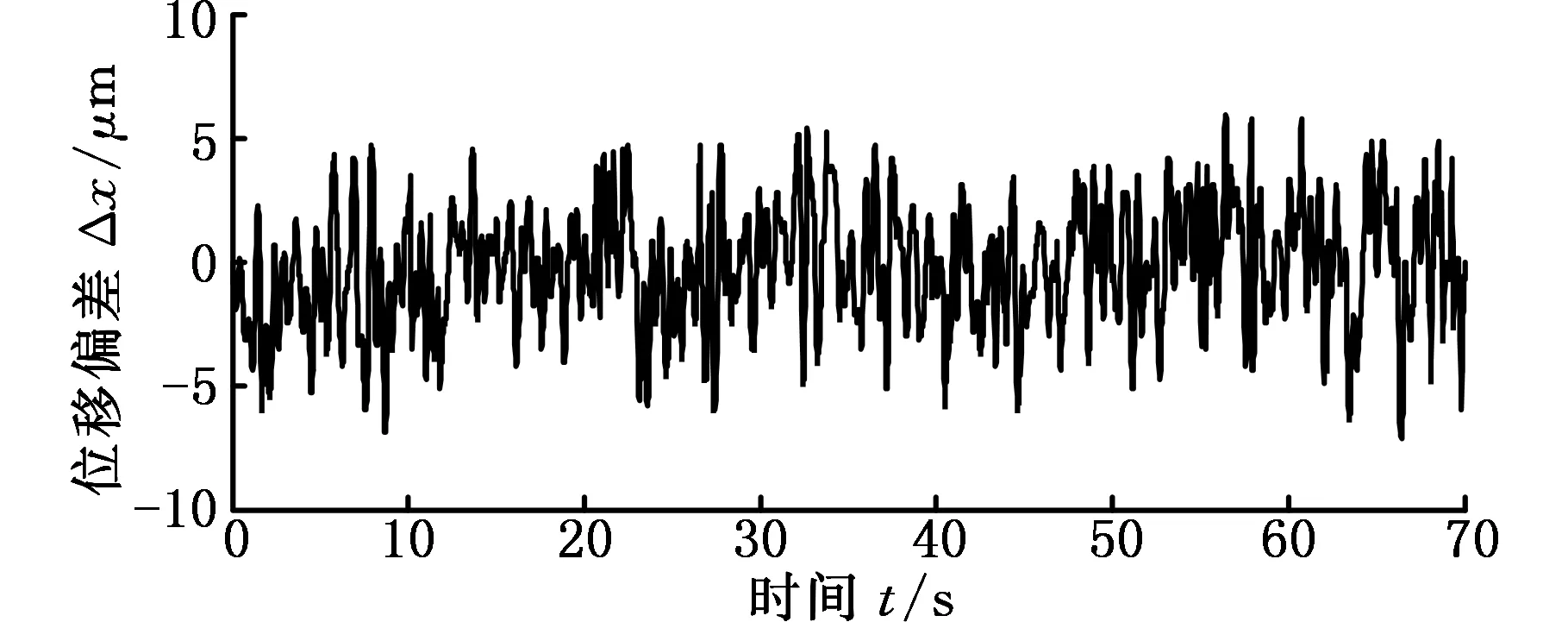
(d)頻域設限切換系統的位移偏差圖7 切換策略對比實驗曲線Fig.7 The contrast experiment curves of switching strategy

[1] CHEN Gang, CAO Sai, JIANG Xintian, et al. Algorithm Research for Increasing Accuracy of Rolling Mill Servo System under the Condition of State Feedback[C]//2015 International Conference on Fluid Power and Mechatronics. Harbin:IEEE,2015:628-632.

[2] SEO J, VENUGOPAL R, KENNE J P. Feedback Linearization Based Control of a Rotational Hydraulic Drive[J]. Control Engineering Practice,2007,15(12):1495-1507.

[3] GOMES D S J M, CASTELAN E B, CORSO J, et al. Dynamic Output Feedback Stabilization for Systems with Sector-bounded Nonlinearities and Saturating Actuators[J]. Journal of the Franklin Institute,2013:464-484.

[4] KOUROSH M T, JAFAR M, ERIK D. Adaptive Control of Cold Rolling System in Electrical Strips Production System with Online-Offline Predictors[J]. Int. J. Adv. Manuf. Technol.,2010(50):917-930.

[5] 蒲明，吳慶憲，姜長生，等．基于模糊干擾觀測器的自適應二階動態滑模控制[J]．控制理論與應用，2011，28(6):805-812． PU Ming, WU Qingxian, JIANG Changsheng, et al. Adaptive Second-order Dynamic Sliding-mode Control based on Fuzzy Disturbance-observer[J]. Control Theory and Applications,2011,28(6):805-812.

[6] OTTO C, PETR H. Adaptive Fuzzy Sliding Mode Control for Electro-hydraulic Servo Mechanism[J]. Expert Systems with Applications,2012,39:10269-10277.

[7] 王益群, 寧淑榮, 劉建. 熱軋立輥電液伺服系統的自 適應模糊控制[J]. 機械工程學報, 2007,43(12):1-4. WANG Yiqun, NING Shurong, LIU Jian. Adapitive Fuzzy Approach to Control the Electro-hydraulic Servo on the Plate Width in Hot Plate Mills[J]. Chinese Journal of Mechanical Engineering,2007,43(12):1-4.

[8] 方一鳴, 李葉紅, 石勝利, 等. 液壓伺服位置系統的神經網絡backstepping控制[J]. 電機與控制學報，2014,18(6):108-115. FANG Yiming, LI Yehong, SHI Shengli, et al. Neural Network Backstepping Control of Hydraulic Servo Position System[J]. Electric Machines and Control, 2014,18(6):108-115.

[9] 李建雄，方一鳴，石勝利. 冷帶軋機液壓伺服系統的魯棒輸出反饋控制[J]. 控制理論與應用, 2012,29(3):331-336. LI Jianxiong, FANG Yiming, SHI Shengli. Robust Output-feedback Control for Hydraulic Servo-position System of Cold-strip Rolling Mill[J]. Control Theory & Applications,2012,29(3):331-336.

[10] CHEN Mou, WU Qingxian, CUI Rongxin. Terminal Sliding Mode Tracking Control for a Class of SISO Uncertain Nonlinear Systems[J]. ISA Transactions,2013,2:198-206.

[11] VLADIMIR M, ZELJKO S, MARIO E. RobustH∞Position Control Synthesis of an Electro-hydraulic Servo System[J]. ISA Transactions,2010,4:535-542.

[12] ZULFATMAN H, MOHD F R, ABDUL R H, et al. Robust Position Tracking Control of an Electro-hydraulic Actuator in the presence of Friction and Internal Leakage[J]. Arabian Journal for Science and Engineering,2014,14:2965-2978.

[13] 王志杰, 方一鳴, 李葉紅, 等. 輸入受限的軋機液壓伺服系統多模型切換控制[J]. 儀器儀表學報,2013,34(4):881-888. WANG Zhijie, FANG Yiming, LI Yehong, et al. Multi-model Switching Control for Rolling Mill Hydraulic Servo System with Input Constraints[J]. Chinese Journal of Scientific Instrument, 2013, 34(4) :881-888.

[14] XIN Jiao, FIDAN B, JU Jiang, et al. Adaptive Mode Switching of Hypersonic Morphing Aircraft Based on Type-2 TSK Fuzzy Sliding Mode Control[J]. Science China Information Sciences,2015,48(7):1-15.

[15] 陳剛，王益群，陳金龍，等. 設限頻域前饋板厚控制策略研究[J]. 機床與液壓，2015，43(17)：11-15. CHEN Gang, WANG Yiqun, CHEN Jinlong, et al. Study on Finite Frequency Domain Feedforward Gauge Control Strategy[J]. Machine Tool & Hydraulics,2015,43(17):11-15.

[16] 鄭大鐘. 線性系統理論[M]. 2版. 北京：清華大學出版社，2012:310-216. ZHENG Dazhong. The Linear System Theory[M]. 2nd ed. Beijing: Tsinghua University Press,2012:310-316.

[17] 陳萍, 熊蔚明, 于世強, 等. 探空火箭通信系統最優信噪比切換閾值的設計[J]. 固體火箭技術,2015,38(4):595-600. CHEN Ping, XIONG Weiming, YU Shiqiang, et al. Design of the Optimum Signal-to-noise Ratio Switch Threshold of Sounding Socket Communication System[J]. Journal of Solid Rocket Technology,2015,38(4):595-600.

(編輯王艷麗)

FiniteFrequencyDomainWeightingSwitchingControlofanElectro-hydraulicPositionControlSystem

CHEN Gang1,2CAO Sai2WANG Yiqun1,2ZHAO Tuanmin3

1.Yanshan University National Engineering Research Center for Equipment and Technology of Cold Strip Rolling, Qinhuangdao,Hebei,066004 2.Institute of Mechanical Engineering, Yanshan University, Qinhuangdao,Hebei,066004 3.Institute of Strip Rolling Equipment, China National Heavy Machinery Research Institute Co., Ltd., Xi’an,710032

The mechanism of the double-order state feedback (DOSF) control system that had static errors was analyzed. A three-order state feedback (TOSF) controller without static errors was designed. To overcome the high order of TOSF control systems, a finite frequency domain weighting switching algorithm was adopted to realize TOSF-DOSF dual-controller switching control. The algorithm might reduce the sensitivity of control action on weighting coefficient changing. Simulations show that the static errors of electro-hydraulic position servo DOSF control system are positive correlation with load elastic stiffnesses and TOSF control system may eliminate static errors in conformity with dynamic performances. Experiments show that the system with TOSF-DOSF dual-controller finite frequency domain weighting switching control has good dynamic and static performances. It has smaller switching impacts compared with threshold switching.

electro-hydraulic position servo; state feedback; static error; switching in finite frequency domain

2016-07-15

國家自然科學基金資助項目(51305389)；國家冷軋板帶裝備及工藝工程技術研究中心開放課題(005004)；國家智能制造專項(發改辦高技[2014]2558)；河北省高等學校創新團隊領軍人才培育計劃資助項目(LJRC013)

TH137;TP278

10.3969/j.issn.1004-132X.2017.17.007

陳剛，男，1979年生。燕山大學機械工程學院副教授、博士。主要研究方向為軋機板厚控制。發表論文20余篇。E-mail：cg_1915@163.com。曹賽，男，1989年生。燕山大學機械工程學院碩士研究生。王益群，男，1938年生。燕山大學機械工程學院教授、博士研究生導師。趙團民，男，1960年生。中國重型機械研究院板帶軋制裝備研究所教授級高級工程師。