有向通弦二部圖的最小秩問(wèn)題研究

牟谷芳

（樂(lè)山師范學(xué)院 數(shù)學(xué)與信息科學(xué)學(xué)院，四川 樂(lè)山 614000）

有向通弦二部圖的最小秩問(wèn)題研究

牟谷芳

（樂(lè)山師范學(xué)院 數(shù)學(xué)與信息科學(xué)學(xué)院，四川 樂(lè)山 614000）

有向二部圖的最小秩問(wèn)題等價(jià)于研究與之對(duì)應(yīng)的符號(hào)模式矩陣的最小秩問(wèn)題。文章研究了具有特殊結(jié)構(gòu)的有向通弦二部圖的最小秩問(wèn)題，而獲得了有向通弦二部圖的最小秩為其團(tuán)覆蓋數(shù)，并將有向二部圖的最小秩問(wèn)題用于職場(chǎng)的雙選會(huì)中。

有向通弦二部圖；符號(hào)模式矩陣；最小秩

0 引言

無(wú)向圖和有向圖廣泛用于特殊矩陣的最小秩計(jì)算中。圖的最小秩問(wèn)題最早是由P.M.Nylen[1]提出來(lái)的，他將實(shí)對(duì)稱(chēng)矩陣與無(wú)向樹(shù)結(jié)合起來(lái)研究了實(shí)對(duì)稱(chēng)矩陣的最小秩問(wèn)題，并給出了求解方法的有效算法。由此，樹(shù)的最小秩問(wèn)題就產(chǎn)生了。之后，S.M.Fallat和L.Hogben等人將無(wú)向樹(shù)的最小秩問(wèn)題推廣到了一般無(wú)向圖的最小秩問(wèn)題[2]。利用無(wú)向圖計(jì)算所有實(shí)對(duì)稱(chēng)矩陣所對(duì)應(yīng)的對(duì)稱(chēng)零-非零模式矩陣的最小秩。由此，將無(wú)向圖的最小秩問(wèn)題自然推廣到了有向圖的最小秩問(wèn)題，利用有向圖來(lái)研究實(shí)非對(duì)稱(chēng)矩陣所對(duì)應(yīng)的非對(duì)稱(chēng)零-非零模式矩陣的最小秩問(wèn)題。由于利用代數(shù)方法計(jì)算特殊矩陣的最小秩較為困難，于是，通過(guò)圖的一些圖參數(shù)（路覆蓋數(shù) P(G)[2]，團(tuán)覆蓋數(shù) CC(G)[2]，零迫集Z(G)[3]，圖的最小度數(shù)[4]，圖的最大匹配數(shù)match(G)[5]等）來(lái)確定圖的最小秩的下界或上界。在文獻(xiàn)[6]中，研究了無(wú)向通弦二部圖的最小秩問(wèn)題，且獲得了無(wú)向通弦二部圖的最小秩為其團(tuán)覆蓋數(shù)。在此基礎(chǔ)上，本文研究了特殊有向通弦二部圖的最小秩問(wèn)題，且獲得了有向通弦二部圖的最小秩為其團(tuán)覆蓋數(shù)，并將有向二部圖的最小秩問(wèn)題應(yīng)用于職場(chǎng)的“雙選”中。

1 預(yù)備知識(shí)

下面介紹符號(hào)模式矩陣和有向通弦二部圖的一些重要定義。

定義1.1[7]設(shè)A=(aij)是一個(gè)n階實(shí)矩陣，以aij的符號(hào){+，-，0}為元素所組成的矩陣稱(chēng)為A的符號(hào)模式矩陣(Sign Pattern)，記為P。由與A有相同符號(hào)模式的所有實(shí)矩陣所組成的集合稱(chēng)為由A所決定的定性矩陣類(lèi) (Qualitative Matrix Class)，記為。

定義1.2[8]設(shè)P是一個(gè)n階符號(hào)模式矩陣，P的最小秩定義為：

其中min表示最小值。

定義1.3[9]一個(gè)圖G由兩部分組成有限的非空頂點(diǎn)集V和邊集E。圖G的階數(shù)是G的頂點(diǎn)個(gè)數(shù)，記為|G|。一個(gè)若無(wú)重邊和環(huán)的圖稱(chēng)為簡(jiǎn)單圖。

定義1.4[9]一個(gè)有向圖是由非空有限集合V與集合E構(gòu)成，記為Γ，其中V中元素為頂點(diǎn)，E中元素為不同頂點(diǎn)的有序?qū)ΓQ(chēng)為弧或有向邊。

定義1.5[9]在一個(gè)有向圖中，有向邊集{{i1，i2}，…{ik-1，ik}}的各個(gè)頂點(diǎn)都不同，稱(chēng)從點(diǎn)i1到點(diǎn)ik的一條路（path），k為路的長(zhǎng)度。若i1與 ik重合則稱(chēng){{i1，i2}，…{ik-1，ik}}為一個(gè)回路。

定義1.6[9]若圖G的頂點(diǎn)集V能夠被分為兩個(gè)子集U，V（稱(chēng)為部集），使得 G的每條邊必然連接U中一個(gè)頂點(diǎn)和V中一個(gè)頂點(diǎn)（記G得邊集為E(G)），稱(chēng)G為二部圖，記為G(U，V)。然而，這并不意味著U中每個(gè)頂點(diǎn)與V中每個(gè)頂點(diǎn)鄰接。

定義1.7[9]設(shè)M是E(G)的子集，如果M中任意兩條邊在G中均不鄰接，則稱(chēng)M是G(U，V)的一個(gè)匹配，并記M所含的邊數(shù)為|M|。

定義 1.8[10]設(shè) G(U，V)為二部圖，P為一符號(hào)模式矩陣，其中，U={1，2，…，n}（對(duì)應(yīng) P的行標(biāo)集）和 V={1′，2′，…，n′}（對(duì)應(yīng)P的列標(biāo)集）。若圖G中的每邊都帶有符號(hào)，則稱(chēng)G為符號(hào)圖，記為 G＝（V，E，sign），且 G（U，V）每邊的符號(hào)由P的符號(hào)來(lái)確定。若P中元素為正，則邊{i，j′}標(biāo)為“+”，i∈U，j′∈V；若P中元素為負(fù)，則邊{i，j′}標(biāo)為“-”，i∈U，j′∈V；若在 P中元素為零，在G(U，V)中不存在邊。

定義 1.9[10]設(shè) G(U，V)=(V，E，sign)為符號(hào)二部圖。若邊的符號(hào)為正，則有向邊{i，j′}∈E，i∈U，j′∈V；若邊的符號(hào)為負(fù)，則有向邊{j′，i}∈E，i∈U，j′∈V，G(U，V)稱(chēng)為有向二部圖。

由有向圖的出度與入度的定義，我們給出了有向二部圖的出度與入度的定義。

定義 1.10 在有向二部圖 G(U，V)中(i∈U，j′∈V)，若（i，j′）∈E，為 G(U，V)的一條邊，則稱(chēng)頂點(diǎn)j′是頂點(diǎn)i一個(gè)鄰接點(diǎn)；若邊{i，j′}的符號(hào)為正時(shí)，稱(chēng)j′是i的一個(gè)“出度點(diǎn)”；若邊{i，j′}的符號(hào)為負(fù)時(shí)，j′是 i的一個(gè)“入度點(diǎn)”。頂點(diǎn)i的所有“出度點(diǎn)”的個(gè)數(shù)，稱(chēng)為i的出度(out degree)，記為 deg+(i)；頂點(diǎn) i的所有“入度點(diǎn)“的個(gè)數(shù)，稱(chēng)為i的入度(in degree)，記為deg-(i)。

定義1.11[6]對(duì)于二部圖G(U，V)（部集為 U={1，2，…，n}和 V={1′，2′，…，n′}），若 U中的每一個(gè)頂點(diǎn)都和V中的每個(gè)頂點(diǎn)連接，則稱(chēng)G(U，V)為完全二部圖 (complete bipartite graph)。

定義1.12[6]若二部圖中不含有長(zhǎng)度為6或大于6的回路，稱(chēng)為通弦(chordal bipartite)二部圖。

定義1.13[6]若二部圖能用r個(gè)完全二部子圖將G(U，V)的所有邊全部覆蓋，且 r最小，則稱(chēng) r為其團(tuán)覆蓋數(shù)，記為bi(G(U，V))，其中，G(U，V)的團(tuán)是其一個(gè)完全二部子圖。

根據(jù)定義1.12和定義1.13，給出有向完全二部圖和有向通弦二部圖的定義。

定義1.14對(duì)于有向二部圖G(U，V)（部集為 U={1，2，…，n}和 V={1′，2′，…，n′}），若 U中的每一個(gè)頂點(diǎn)都和V中的每個(gè)頂點(diǎn)連接，且U中的每一個(gè)頂點(diǎn)為出度點(diǎn)（或V中的每一個(gè)頂點(diǎn)為出度點(diǎn)），則稱(chēng)G(U，V)為有向完全二部圖(directed complete bipartite graph)，若｜U｜=s，｜V｜=t有向完全二部圖可記為 Ks，t。

定義1.15 若有向二部圖中不含有長(zhǎng)度為6或大于6的有向回路，稱(chēng)為有向通弦(directed chordal bipartite)二部圖。

引理1.16[6]對(duì)任意帶有完美匹配M的通弦二部圖 G(U，V)，它的團(tuán)覆蓋數(shù) bi(G(U，V))=｜M｜。

引理1.17[6]設(shè)G(U，V)是一個(gè)無(wú)向二部圖，則它的最小秩 mr(G(U，V))≤bi(G(U，V))。

引理1.18[6]設(shè)G(U，V)是一個(gè)無(wú)向通弦二部圖，則它的最小秩

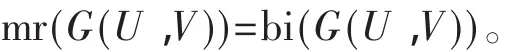
2 有向通弦二部圖的最小秩

對(duì)于一般有向圖的最小秩問(wèn)題目前還沒(méi)有很好的解決方法。近些年來(lái)，在符號(hào)圖的最小秩研究問(wèn)題中，主要是研究特殊圖的最小秩計(jì)算方法和最小秩的上下界。本文在無(wú)向通弦二部圖的最小秩問(wèn)題的研究基礎(chǔ)上，研究了有向通弦二部圖的最小秩問(wèn)題，并將有向二部圖的最小秩應(yīng)用于實(shí)際問(wèn)題中。

引理2.1 若有向二部圖G(U，V)為 n-有向回路，則 mr(G(U，V))=n-1。

證明：設(shè) G(U，V)為 n-有向回路，它所對(duì)應(yīng)的符號(hào)模式矩陣為

在P的行列展開(kāi)式中有兩非零項(xiàng)，且符號(hào)不同，則mr(P)≠n，同時(shí) P中含有一個(gè) n-1階的下三角矩陣，則mr(P)=n-1，故有向二部圖G(U，V)的最小秩 mr(G(U，V))=n-1。

特別地，當(dāng)k≤4時(shí)，G(U，V)為有向通弦二部圖，且它的最小秩為1。

引理 2.2 若有向二部圖 G(U，V)為 n階完全有向二部圖，則mr(G(U，V))=1。

證明：根據(jù)定義 1.14知，n階完全有向二部圖G(U，V)所對(duì)應(yīng)的符號(hào)模式矩陣各元素的符號(hào)都相同，則mr(G(U，V))=1。

定理2.3 設(shè)G(U，V)是一個(gè)有向二部圖，則它的最小秩 mr(G(U，V))≤bi(G(U，V))。

證明：設(shè) G(U，V)中的團(tuán)覆蓋數(shù)為 r，構(gòu)建每一個(gè)團(tuán)所對(duì)應(yīng)的符號(hào)模式矩陣Pi(i=1，2，..，r)，且每個(gè)矩陣的最小秩為1。再將這些矩陣相加得到一個(gè)新矩陣P，它所對(duì)的二部圖為G(U，V)，顯然 mr(P)≤r。故 G(U，V)的最小秩 mr(G(U，V))≤bi(G(U，V))。

定理2.4 設(shè)G(U，V)是一個(gè)有向二部團(tuán)塊圖，且每個(gè)團(tuán)圖為k-有向回路（k≤4）或?yàn)橥耆邢蚨繄D，則它的最小秩mr(G(U，V))=bi(G(U，V))。

證明：根據(jù)引理2.1和引理2.2知，mr(G(U，V))≥bi(G(U，V))再由定理2.3 可得 mr(G(U，V))=bi(G(U，V))。

定理2.5 在一個(gè)有向通弦二部圖G(U，V)中，若 G(U′，V′)是 G(U，V)中帶有唯一完美匹配M′的最大子圖，則

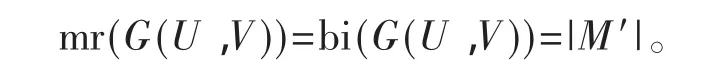
證明：若 G(U′，V′)=G(U，V)，結(jié)論顯然成立。

若 G(U′，V′)≠G(U，V)，首先尋找 G(U，V)中的通弦二部子圖K2.2，設(shè)團(tuán)數(shù)為r。然后刪除這些團(tuán)，得二部圖為G(U″，V″)。利用文獻(xiàn)[10]算法3.1尋找?guī)в形ㄒ煌昝榔ヅ銶″的最大子圖，則｜M′｜=｜M″｜+r。

根據(jù)引理2.2和定理2.4，結(jié)論成立。

3 應(yīng)用

圖的最小秩問(wèn)題廣泛應(yīng)用于通信網(wǎng)絡(luò)和信息科學(xué)中[11-12]，尤其在通信復(fù)雜度上有重要應(yīng)用，如在文獻(xiàn)[11]中，利用符號(hào)模式的最小秩確定了通信復(fù)雜度的一個(gè)下界。本節(jié)將通弦二部圖的最小秩問(wèn)題應(yīng)用于職場(chǎng)招聘會(huì)的雙選中。

例3.1 設(shè)有5位大學(xué)畢業(yè)生：A1，A2，A3，A4，A5，某企業(yè)公開(kāi)招聘的崗位有顧問(wèn)，編輯，程序員，秘書(shū)，培訓(xùn)師五個(gè)崗位。為了方便后面的敘述，將畢業(yè)生與不同崗位進(jìn)行編號(hào)：A1，A2，A3，A4，A5，分別對(duì)應(yīng) 1，2，3，4，5；顧問(wèn)，編輯，程序員，秘書(shū)，培訓(xùn)師分別對(duì)應(yīng) 1′，2′，3′，4′，5′。在職場(chǎng)招聘會(huì)上，不同的畢業(yè)生和各個(gè)崗位對(duì)應(yīng)的情況如下：

1∶2′，3′；2∶1′，2′，4′，5′；3∶2′，3′；4∶2′，3′；5∶4′，5′。

假設(shè)每個(gè)崗位只招一人，試問(wèn)每個(gè)畢業(yè)生是否能夠挑選到合適的工作？

圖1 二部圖G(U，V)

圖2 G(U，V)的完美匹配

方案：畢業(yè)生與崗位對(duì)應(yīng)的情況利用二部圖G(U，V)（如圖1所示）來(lái)建立模型，其中U={1，2，3，4，5}，V={1′，2′，3′，4′，5′}。容易判斷G(U，V)是無(wú)向通弦二部圖，且團(tuán)覆蓋數(shù)為3。由引理2.2知，G(U，V)的最小秩為3。因此，至少有3位畢業(yè)生能找到合適工作。但是圖1中的完美匹配不是唯一的，故不是每個(gè)人都能夠找到合適的工作。

根據(jù)文獻(xiàn)[10]算法3.1，在圖3中能夠找到一個(gè)最大唯一完美匹配（如圖2所示）：

M′∶{{1，2′}，{2，1′}，{3，3′}，{5，5′}}。

因此，A1，A2，A3，A5 能找到合適的崗位，且分別對(duì)應(yīng)的崗位為編輯，顧問(wèn)，程序員，培訓(xùn)師。

在工作崗位招聘過(guò)程中，不僅畢業(yè)生想要挑選一份滿意的工作，而且工作崗位對(duì)畢業(yè)生也有不同的要求，比如英語(yǔ)水平、計(jì)算機(jī)等級(jí)水平和專(zhuān)業(yè)技術(shù)水平等因素，工作崗位也要挑合適的人選，即為校園招聘“雙選會(huì)”。因此，我們將有向通弦二部圖的最小秩問(wèn)題應(yīng)用于職場(chǎng)“雙選會(huì)”的研究中。

例3.2 設(shè)有4位大學(xué)畢業(yè)生：A1，A2，A3，A4，某企業(yè)公開(kāi)招聘的崗位有編輯，程序員，秘書(shū)，培訓(xùn)師4個(gè)崗位。將畢業(yè)生與不同崗位進(jìn)行編號(hào)：A1，A2，A3，A4，分別對(duì)應(yīng)1，2，3，4；編輯，程序員，秘書(shū)，培訓(xùn)師分別對(duì)應(yīng) 1′，2′，3′，4′。在職場(chǎng)招聘會(huì)上，不同的畢業(yè)生挑選不同崗位的情況如下：

1∶1′，2′，3′，4′；2∶1′，3′；3∶1′，2′；4∶1′，4′。

反之，不同的工作崗位挑選不同人選的情況如下：

2′∶2，4；3′∶3，4；4′∶2，3。

假設(shè)每個(gè)崗位只招一人，試問(wèn)每個(gè)畢業(yè)生是否能夠挑選到合適的工作？ 反之，工作崗位能否招到合適的人員？

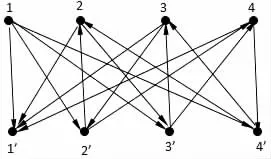
圖3 有向二部圖G(U，V)

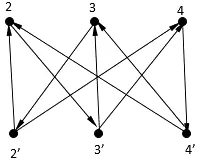
圖4 有向二部子圖G(U1，V1)

方案：畢業(yè)生與崗位對(duì)應(yīng)的情況利用有向二部圖G(U，V)（如圖3所示）來(lái)建立模型，其中 U={1，2，3，4，}，V={1′，2′，3′，4′}。與 G(U，V)所對(duì)應(yīng)的符號(hào)模式矩陣為

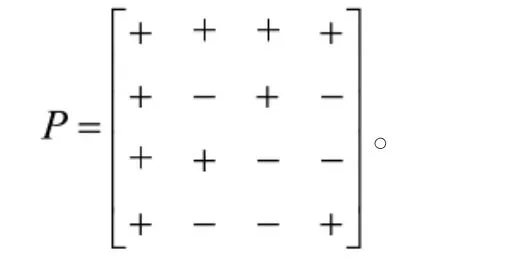
將P用于職場(chǎng)“雙選會(huì)”的研究中，可以從如下兩個(gè)方面來(lái)考慮。

一方面考慮每個(gè)畢業(yè)生能否挑選到自己滿意的工作。

根據(jù)畢業(yè)生挑選的崗位情況 1∶1′，2′，3′，4′；2∶1′，3′；3∶1′，2′；4∶1′，4′可知，在有向二部圖G(U，V)中不能夠找到一個(gè)最大唯一完美匹配。因此，不是每個(gè)人能夠找到合適的工作。若在G(U，V)的U和 V中分別刪除頂點(diǎn)1和 1′，得到子圖G(U1，V1)（見(jiàn)圖4）。在G(U1，V1)中能夠找到一個(gè)最大唯一完美匹配（如圖5所示）：

M′＝{{2，3′}，{3，2′}，{4，4′}}。

因此，A2，A3，A4能找到合適的崗位，且分別對(duì)應(yīng)的崗位為秘書(shū)，程序員，培訓(xùn)師。

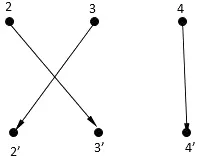
圖5 最大完美匹配

圖6 最大完美匹配

另一方面考慮每個(gè)工作崗位能否挑選到合適的人選。

根據(jù)畢業(yè)生挑選的崗位情況 2′∶2，4；3′∶3，4；4′∶2，3 可知，在有向二部圖 G(U1，V1)中能夠找到一個(gè)最大唯一完美匹配（如圖6所示）：

M″∶{{2′，4}，{3′，3}，{4′，2}}。

因此，培訓(xùn)師，秘書(shū)，程序員能找到合適的人選，且分別對(duì)應(yīng)的人選為A2，A3，A4。

容易判斷G(U，V)是有向通弦二部圖，且團(tuán)覆蓋數(shù)為3。由定理2.4知，G(U，V)的最小秩為3。因此，有3位畢業(yè)生能找到合適工作和3個(gè)崗位能夠找到合適的人員。

（本文部分內(nèi)容系筆者2015年電子科技大學(xué)博士畢業(yè)論文《矩陣完備化和圖的最小秩問(wèn)題》）

[1]NYLEN P M.Minimum-rank matrices with prescribed graph[J].Linear Algebra Appl.，1996，248：303-316.

[2]FALLAT S M，統(tǒng) HOGBEN L.Theminimum rank of symmetric matrices described by a graph：a survey[J].Linear Algebra Appl.，2007，426:558-582.

[3]HOGBEN L.Minimum rank problems[J].Linear Algebra Appl.，2010，432:1961-1974.

[4]AIM Minimum Rank-Special Graphs Work Graph.Zero forcing sets and theminimum rank of graphs[J].Linear Algebra Appl.，2008，428：1628-1648.

[5]IMA-ISU Research Group.Minimum rank of skew-symmetric matrices described by a graph[J].Linear Algebra Appl.，2009，432：2457-2472.

[6]JOHNSON C R，MILLER J.Rank decomposition under combinatorial constraints[J].Linear Algebra&Its Applications，1997，251：97-104.

[7]DEALBA L M，HARDY T L，HENTZEL I R，et al.Minimum rank and maximum eigenvalue multiplicity of symmetric tree sign patterns[J].Linear Algebra Appl.，2006，418：389-415.

[8]LI Z S，GAO Y B，ARAV M，et al.Sign patterns withminimum rank two and upper boundsonminimum ranks[J].Linear Multilinear A.，2014，61：895-908.

[9]張先迪，李正良.圖論及其應(yīng)用[M].北京：高等教育出版社，2005：2.

[10]牟谷芳，黃廷祝.符號(hào)有向圖的最大SNS-符號(hào)模式矩陣[J].工程數(shù)學(xué)學(xué)報(bào)，2015（5）：772-782.

[11]BURGARTH D，ALESSANDRO D D，HOGBEN L.Zero forcing，linear and quantum controllability for systems evolving on networks[J].Automatic Control，IEEE Transactions on，2013，58:773-784.

[12]LINIAL N，MENDELSON S，SCHECHTMAN G，et al.Complexity measures of sign matrices[J].Combinatorica，2007，27：439-463.

The Minimum Rank Problem Research of Directed Chordal Bipartite Graph

MU Gufɑnɡ
（School of Mathematics and Information Science,Leshan Normal University,Leshan Sichuan 614000,China）

Theminimum rank problem of directed bipartite graph is equivalent to the correspondingminimum rank problem of symbolic pattern matrix.In this paper，theminimum rank problem of directed chordal bipartite graph with a special structure has been studied.In this case,theminimum rank of a directed chordal bipartite graph is its clique coverage number.Beside，theminimum rank problem of directed chordal bipartite graph is used in job fair based on mutual selection.

Directed Chordal Bipartite Graph；Symbolic Pattern Matrix；Minimal Rank

O157.6

A

1009-8666（2017）08-0005-06

［責(zé)任編輯、校對(duì)：李書(shū)華］

10.16069/j.cnki.51-1610/g4.2017.08.002

2017-04-13

四川省教育廳資助科研項(xiàng)目“有向圖的最小秩問(wèn)題及其在通信網(wǎng)絡(luò)中的應(yīng)用”（17ZB0193）；樂(lè)山師范學(xué)院資助科研項(xiàng)目“有向圖的最小秩問(wèn)題及其應(yīng)用”（Z1521)

牟谷芳（1981—），女，土家族，湖北恩施人。樂(lè)山師范學(xué)院數(shù)學(xué)與信息科學(xué)學(xué)院講師，博士，研究方向：組合矩陣論。